【五一创作】【Simulink】采用延时补偿的三相并网逆变器FCS-MPC
👉 【Simulink】基于FCS-MPC的三相并网逆变器控制
上一篇博客介绍了FCS-MPC的基本操作,并且以三相并网逆变器为控制对象进行了Simulink仿真。
但实际仿真中没有考虑补偿延时。本篇博客将讨论为什么要考虑延时并进行补偿,最后对此仿真验证。
传统FCS-MPC
模型预测电流控制步骤:
1)测量负载电流;
2) 针对所有可能的开关状态预测下一采样时刻的负载电流;
3) 评估每个预测的成本函数;
4) 选择使代价函数最小化的切换状态;
5) 应用新的开关状态。
对于三相并网逆变器,代价函数为:
g
i
=
∣
i
α
∗
(
k
+
1
)
−
i
α
p
(
k
+
1
)
∣
+
∣
i
β
∗
(
k
+
1
)
−
i
β
p
(
k
+
1
)
∣
g_i = |i_\alpha^*(k+1)-i_\alpha^p(k+1)|+|i_\beta^*(k+1)-i_\beta^p(k+1)|
gi=∣iα∗(k+1)−iαp(k+1)∣+∣iβ∗(k+1)−iβp(k+1)∣
g i g_i gi 的下标 i 代表开关状态顺序(1-8), i α ∗ i_\alpha^* iα∗ 和 i β ∗ i_\beta^* iβ∗ 的下标 α , β \alpha,\beta α,β 为三相负载电流的 α , β \alpha,\beta α,β 分量(经过Clarke变换),上标 * 表示参考值,上标 p 表示预测值。
为什么要考虑延时补偿?
图源:《Delay Compensation in Model Predictive Current Control of a Three-Phase Inverter》
a. 无延迟:计算时间为零(理想情况下):
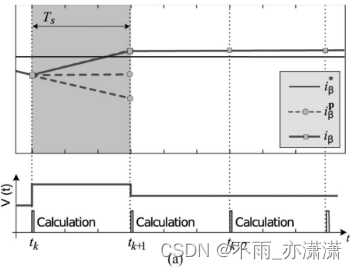
在 k 时刻测量电流,并且立即计算并应用最佳开关状态,在 k+1 时刻达到使误差最小化的切换状态。
(图中 k 到 k+1 时刻共有3条
i
β
p
i_\beta^p
iβp,其中最上面的一条离
i
β
p
i_\beta^p
iβp (水平直线)最近,所以选择最上面的
i
β
p
i_\beta^p
iβp 对应的开关状态,在 k+1 时刻应用)
b. 有延迟且无补偿:计算时间长(实际情况):
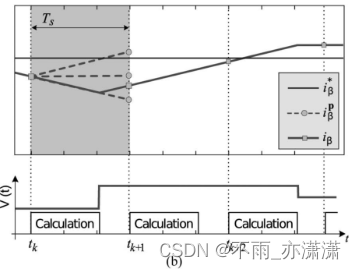
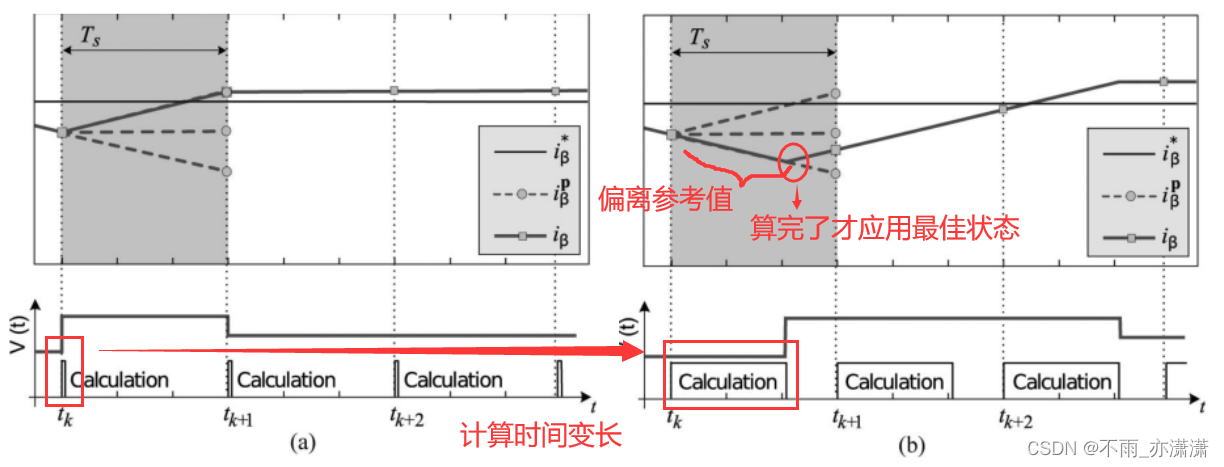
如果计算时间比采样时间长,则在测量电流的瞬间与应用新开关状态的瞬间之间会有延迟。在这两个瞬间之间的间隔期间,将继续应用先前的切换状态。根据 k 处的测量值选择的电压矢量将在 k+1 之后继续应用,从而使负载电流远离参考值。由于该延迟,负载电流将围绕其参考值振荡,从而增加电流纹波。
c. 带延迟和补偿:计算时间长(实际情况):
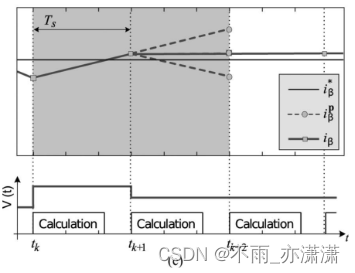
使用在 k 时刻处测量的电流 i(k) 和 施加的开关状态x_opt 来估计在 k+1 时刻处的负载电流的值,并以在 k+1 时刻处估计的负载电流的值预测 k+2 时刻的负载电流,对应的开关状态在 k+1 ~ k+2 时刻应用。
控制算法被修改如下:
1) 负载电流的测量;
2) 切换状态的应用(在前一个间隔中计算);
3) 考虑所施加的开关状态,估计在时间 k+1 处的电流值;
4) 针对所有可能的开关状态预测下一个采样时刻 k+2 的负载电流;
5) 对每个预测的成本函数进行评估;
6) 选择使成本函数最小化的切换状态。

代价函数从
g
i
=
∣
i
α
∗
(
k
+
1
)
−
i
α
p
(
k
+
1
)
∣
+
∣
i
β
∗
(
k
+
1
)
−
i
β
p
(
k
+
1
)
∣
g_i = |i_\alpha^*(k+1)-i_\alpha^p(k+1)|+|i_\beta^*(k+1)-i_\beta^p(k+1)|
gi=∣iα∗(k+1)−iαp(k+1)∣+∣iβ∗(k+1)−iβp(k+1)∣
变成
g
i
=
∣
i
α
∗
(
k
+
2
)
−
i
α
p
(
k
+
2
)
∣
+
∣
i
β
∗
(
k
+
2
)
−
i
β
p
(
k
+
2
)
∣
g_i = |i_\alpha^*(k+2)-i_\alpha^p(k+2)|+|i_\beta^*(k+2)-i_\beta^p(k+2)|
gi=∣iα∗(k+2)−iαp(k+2)∣+∣iβ∗(k+2)−iβp(k+2)∣
以此预测电流
i
α
p
(
k
+
1
)
,
i
β
p
(
k
+
1
)
i_\alpha^p(k+1), i_\beta^p(k+1)
iαp(k+1),iβp(k+1)
仿真
原理图
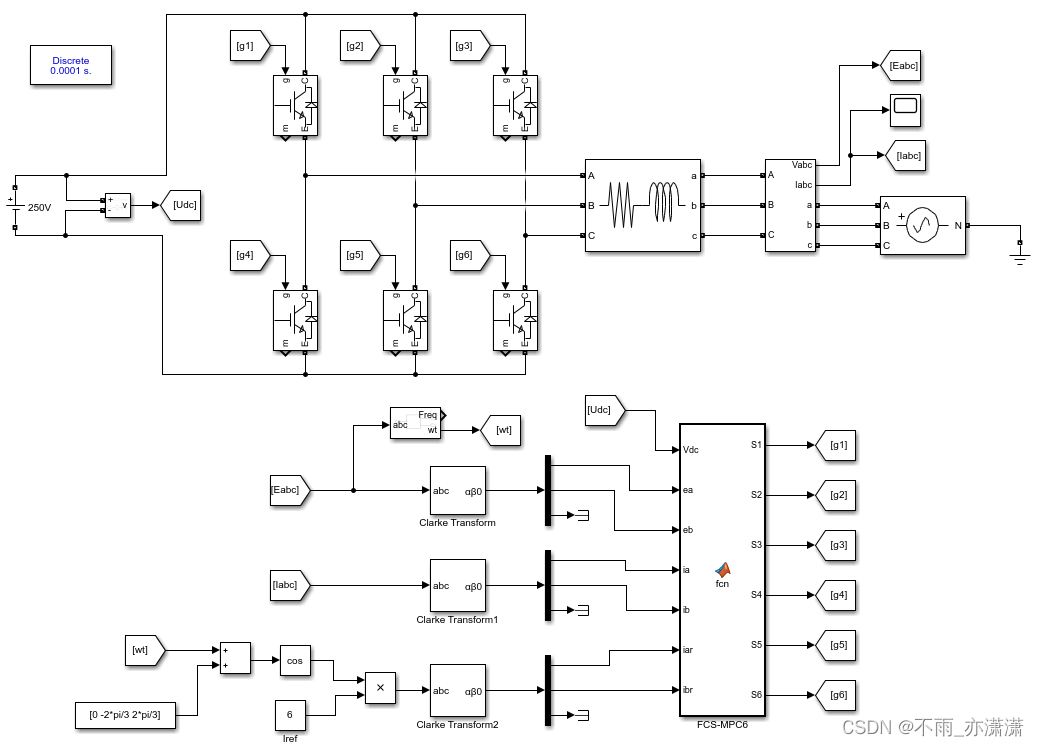
Matlab Function代码
function [S1,S2,S3,S4,S5,S6] = fcn(Vdc, ea, eb, ia, ib, iar, ibr)
g = zeros(1,8);
L = 0.02;
R = 0.05;
T = 1/1e4;
v0 = 0;
v1 = 2/3*Vdc;
v2 = 1/3*Vdc + 1j/sqrt(3)*Vdc;
v3 = -1/3*Vdc + 1j/sqrt(3)*Vdc;
v4 = -2/3*Vdc;
v5 = -1/3*Vdc - 1j/sqrt(3)*Vdc;
v6 = 1/3*Vdc - 1j/sqrt(3)*Vdc;
v7 = 0;
v = [v0 v1 v2 v3 v4 v5 v6 v7];
states = [0 0 0; 1 0 0; 1 1 0; 0 1 0; 0 1 1; 0 0 1; 1 0 1; 1 1 1];
persistent x_opt
if isempty(x_opt)
x_opt = 1;
end
S1 = states(x_opt,1);
S2 = states(x_opt,2);
S3 = states(x_opt,3);
S4 = ~states(x_opt,1);
S5 = ~states(x_opt,2);
S6 = ~states(x_opt,3);
% 负载电流估算
ia1 = (1-T*R/L)*ia+(real(v(x_opt))-ea)*T/L;
ib1 = (1-T*R/L)*ib+(imag(v(x_opt))-eb)*T/L;
for i = 1: 8
v_o1 = v(i);
% 负载电流预测
ia2 = (1-T*R/L)*ia1+(real(v_o1)-ea)*T/L;
ib2 = (1-T*R/L)*ib1+(imag(v_o1)-eb)*T/L;
% 代价函数
g(i) = abs(iar - ia2) + abs(ibr - ib2);
end
[~,x_opt] = min(g);
仿真结果
负载电流
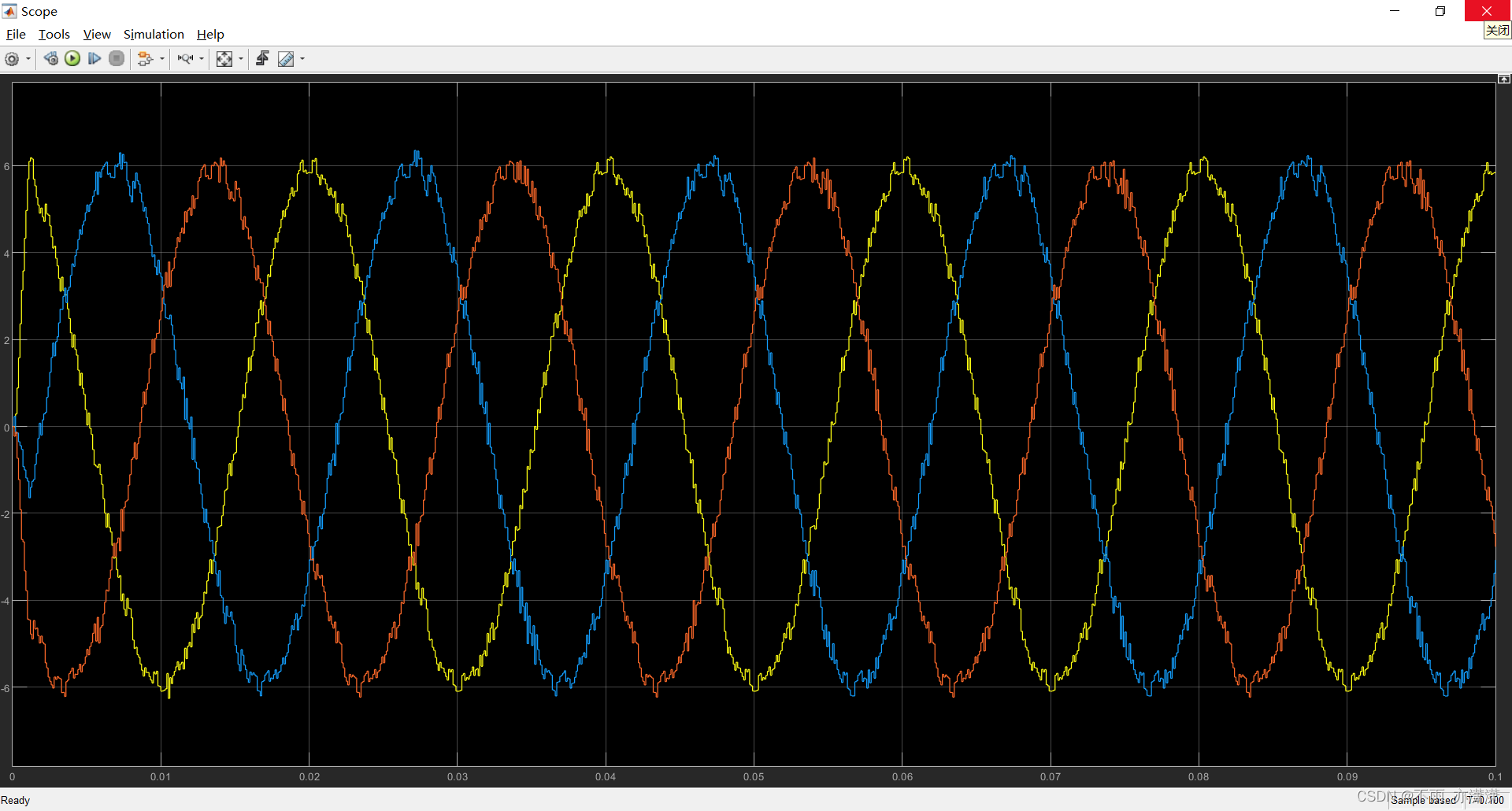
THD降低了一点点,从原来的4.07%降到3.99%,三相的不明显,对于单相的比较明显
遗留问题:
有的论文提到需要对电流参考值和电网电压进行估计,我用了矢量角的方法进行估计后THD反而增大了,很奇怪。
参考:
[1] 郑文帅. 三相并网逆变器有限控制集模型预测控制研究[D].辽宁工程技术大学,2021.DOI:10.27210/d.cnki.glnju.2021.000395.
[2] P. C, J. R, C. S, et al. Delay Compensation in Model Predictive Current Control of a Three-Phase Inverter[J]. IEEE Transactions on Industrial Electronics, 2012,59(2): 1323-1325.
[3] 对同一个三相逆变器使用FCS-MPC的延迟补偿的两种方法
