当前位置：首页 > article >正文

树的刷题,嗝

article 2024/11/14 21:54:50

今天忘记带本子了,就没有学习java了,于是一心刷题,好烦遇到了两个奇怪的题目,我没跟题解写的,但是我是没想到奇怪的样例.

no.1

617. 合并二叉树

难度简单1221收藏分享切换为英文接收动态反馈

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

示例 1：

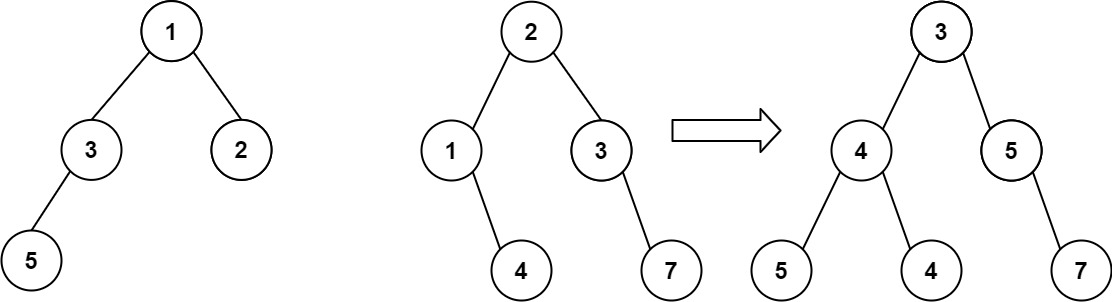
输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

示例 2：

输入：root1 = [1], root2 = [1,2]
输出：[2,2]

提示：

两棵树中的节点数目在范围 [0, 2000] 内
-104 <= Node.val <= 104

我本来也不太会,想着如何把子节点变换,直到看到了题解里面,函数的返回值是节点指针,于是我悟了

一下就会应用了

struct TreeNode* mergeTrees(struct TreeNode* root1, struct TreeNode* root2){
   
   if(root1==NULL){
       return root2;
   }
   if(root2==NULL){
       return root1;
   }
struct TreeNode* root3= (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root3->val=root1->val+root2->val;
    root3->left=mergeTrees(root1->left,root2->left);
    root3->right=mergeTrees(root1->right,root2->right);
    return root3;
}

左节点空的的,返回右节点

反之

要是都不为空就定义节点等于root1+root2,从根节点开始

遍历下去,最后root3就是新的合并树的头节点

no.2

剑指 Offer II 047. 二叉树剪枝

难度中等71收藏分享切换为英文接收动态反馈

给定一个二叉树 根节点 root ，树的每个节点的值要么是 0，要么是 1。请剪除该二叉树中所有节点的值为 0 的子树。

节点 node 的子树为 node 本身，以及所有 node 的后代。

示例 1:

输入: [1,null,0,0,1]
输出: [1,null,0,null,1] 
解释: 
只有红色节点满足条件“所有不包含 1 的子树”。
右图为返回的答案。

示例 2:

输入: [1,0,1,0,0,0,1]
输出: [1,null,1,null,1]
解释:

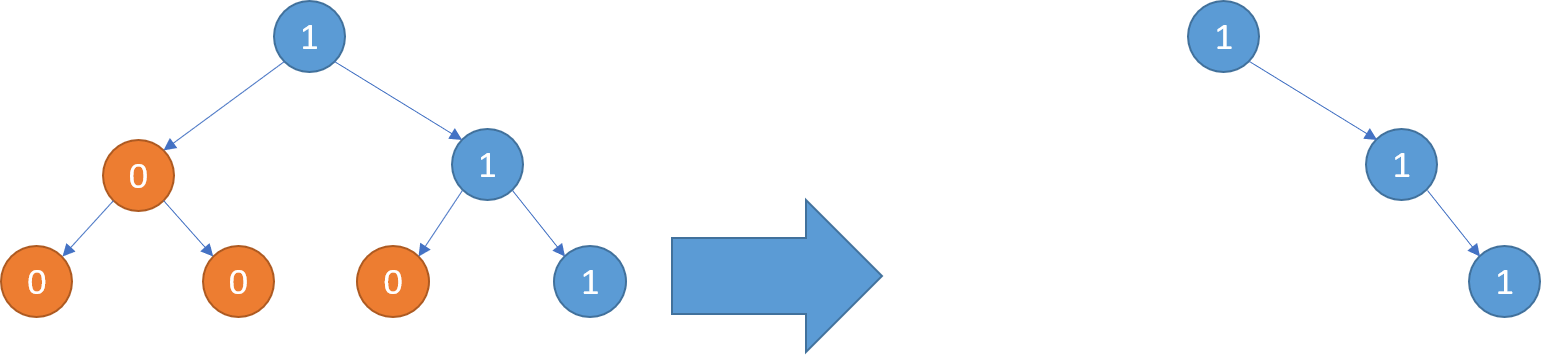
示例 3:

输入: [1,1,0,1,1,0,1,0]
输出: [1,1,0,1,1,null,1]
解释:

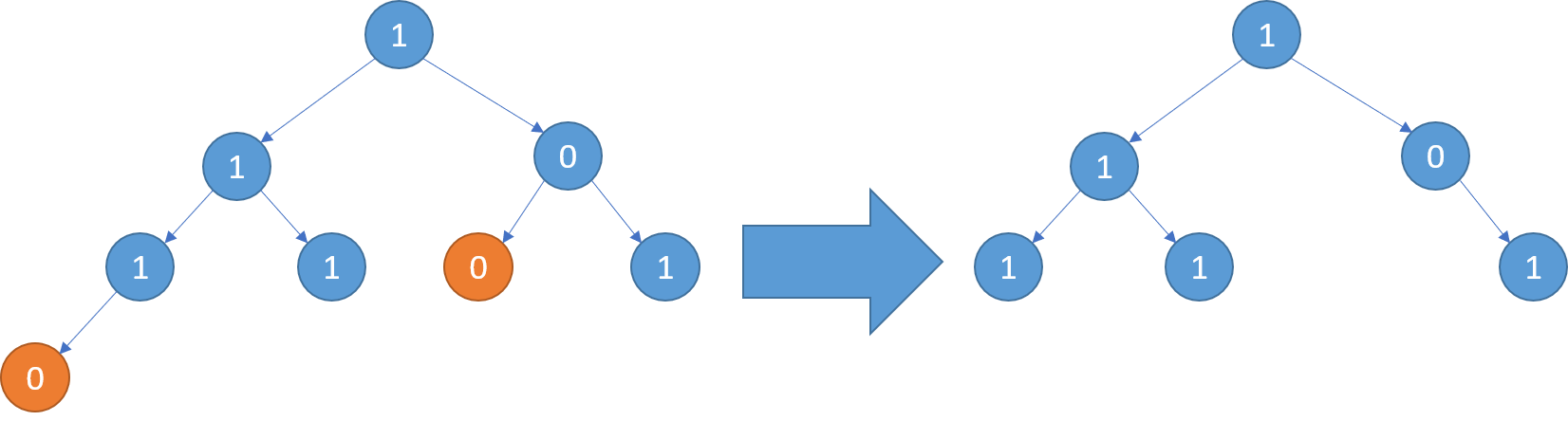
提示:

二叉树的节点个数的范围是 [1,200]
二叉树节点的值只会是 0 或 1

依旧以节点指针返回

对节点的left,以及right遍历判断,要是不是0就返回原来的指针

要是0就返回NULL

这个思想就是好

struct TreeNode* pruneTree(struct TreeNode* root){
   if(root==NULL){//空的返回
       return NULL;
   }

  root->left=pruneTree(root->left);//往下查
  root->right=pruneTree(root->right);//往下查
if(root->left==NULL&&root->right==NULL&&root->val==0){//发现是0且是根节点,直接变成null
      return NULL;
  }
   return root;
}

可以删除的点就是为根节点,且值等于0,而且下面的节点先删了,上面的到就是根节点了,也是向下搜索

代码短就是爽,理解到位直接干废

no.3

力扣嘉年华上的 DIY 手工展位准备了一棵缩小版的二叉装饰树 root 和灯饰，你需要将灯饰逐一插入装饰树中，要求如下：

完成装饰的二叉树根结点与 root 的根结点值相同
若一个节点拥有父节点，则在该节点和他的父节点之间插入一个灯饰（即插入一个值为 -1 的节点）。具体地：
在一个父节点 x 与其左子节点 y 之间添加 -1 节点，节点 -1、节点 y 为各自父节点的左子节点，
在一个父节点 x 与其右子节点 y 之间添加 -1 节点，节点 -1、节点 y 为各自父节点的右子节点，
现给定二叉树的根节点 root ，请返回完成装饰后的树的根节点。
示例 1：

输入：
root = [7,5,6]

输出：[7,-1,-1,5,null,null,6]

解释：如下图所示，

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/KnLfVT
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

和上面的差不多的,判断是否要插入装饰,左节点不空就插入,右节点不空就插入一个

让当前节点的儿子等于新建的节点,新建的节点调用,自己使得下面的节点指向新建的装饰

struct TreeNode* expandBinaryTree(struct TreeNode* root){

    if(root==NULL){
        return NULL;
    }
    if(root->right==NULL&&root->left==NULL){
         return root;
    }

    struct TreeNode* roots1=(struct TreeNode*)malloc(sizeof(struct TreeNode));
    struct TreeNode* roots2=(struct TreeNode*)malloc(sizeof(struct TreeNode));

    if(root->left!=NULL){
     roots1->val=-1;
    roots1->left=expandBinaryTree(root->left);
    roots1->right=NULL;
    }
    if(root->right!=NULL){
    roots2->val=-1; 
    roots2->left=NULL;
    roots2->right=expandBinaryTree(root->right);
    }
    if(root->left!=NULL){
        root->left=roots1;
    }
    if(root->right!=NULL){
        root->right=roots2;
    }
    

    return root;

但是千千万万注意逻辑顺寻 ,不要搞错了,有课逻辑就完全的ok了

no.4

剑指 Offer 55 - II. 平衡二叉树

难度简单354收藏分享切换为英文接收动态反馈

输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

返回 true 。

示例 2:

给定二叉树 [1,2,2,3,3,null,null,4,4]

返回 false 。

限制：

0 <= 树的结点个数 <= 10000

看了一会想想了想,才相信确实是求高度,和昨天的好像是一毛一样的呀,我试着我把代码,拿来搞了一下额,直接过了

bool isBalanced(struct TreeNode* root){
 int l=1;
  dfs(root,&l);
  if(l==1)
   return true;
   else
   return false;
}
int max(int a,int b){
     if(a>b)
     return a;
     else
     return b;
 }

int dfs(struct TreeNode* root,int* l){
  if(root==NULL){
      return 0;
  }

  int ll=dfs(root->left,l)+1;
  int r=dfs(root->right,l)+1;
   
  if(abs(ll-r)>1){
  *l=0;
  
  }

 return max(ll,r);

}

还来一句求高度,你会了吗?简单的递归思想

no.5

剑指 Offer 26. 树的子结构

难度中等741收藏分享切换为英文接收动态反馈

输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)

B是A的子结构，即 A中有出现和B相同的结构和节点值。

例如:
给定的树 A:

3 / \ 4 5 / \ 1 2
给定的树 B：

4 / 1
返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。

示例 1：

输入：A = [1,2,3], B = [3,1]
输出：false

示例 2：

输入：A = [3,4,5,1,2], B = [4,1]
输出：true

限制：

0 <= 节点个数 <= 10000

我的思想是,找了一点与节点的值相同就往下查,动态的遍历,左和右边的遍历都是对的就可以修改false,但是没有过,报错的样例,我自己运行了答案是对的

无语了

bool b=false;

bool dfs(struct TreeNode* A, struct TreeNode* B){
      if(B==NULL){
        return true;
      }
      if(A==NULL){
          return false;
      }
      if(B->val==A->val&&b==false){
         bool r=dfs(A->right,B->right);
         bool l=dfs(A->left,B->left);
         if(r==true&&l==true){
             b=true;
             return true;
         }
         else{
             b=false;
             return false;
         }
      }
      if(A->left!=NULL)
      dfs(A->left,B);
      if(A->right!=NULL)
      dfs(A->right,B);
      return false;
}


bool isSubStructure(struct TreeNode* A, struct TreeNode* B){

  dfs(A,B);
if(B==NULL){
    return false;
}
  return b; 

}

搜索到底向上返回bool,一直是true答案就会是true,但是遍历得到了0,那就往上返回的就是0

就算变成了true也会变成false,而且是找的了相等才会往下遍历 ,而且要是查到B为NULL那就是true 我觉得完全是对的,可以样例不让过,还给的神奇的样例.

ok今天完结哈哈!

查看全文

http://www.kler.cn/a/16849.html