第四章 数据关联分析方法

基本概念和方法

关联规则和算法应用

基本概念和术语

关联规则算法应用：

一个关联规则分析的例子—————超市购物篮分析

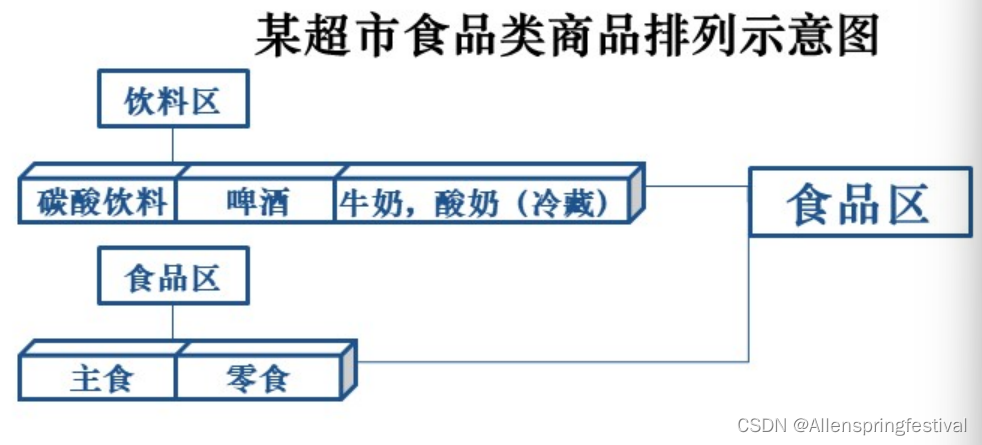
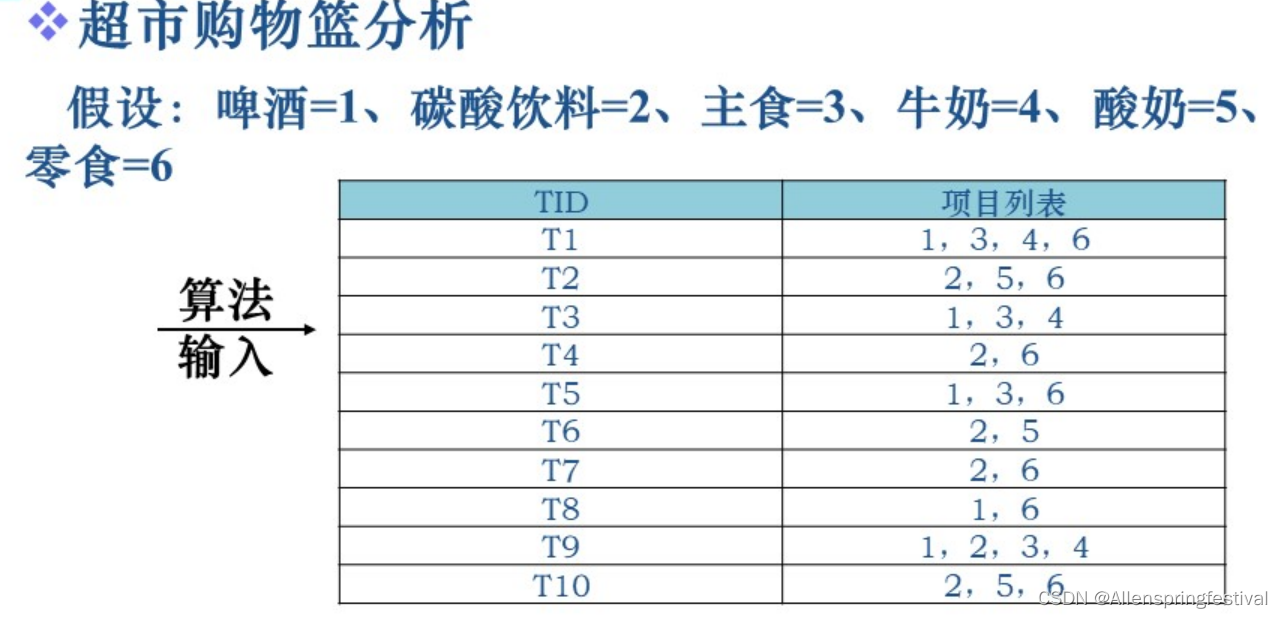
 不要看

后面数字看不懂

 项集：是指项的集合。包含k个项的项集称为k-项集

支持度：若A是一个项集，则A的支持度表示在所有事务T中同时出现A项集的概率

置信度：A出现的次数除以A和B同时出现的次数。

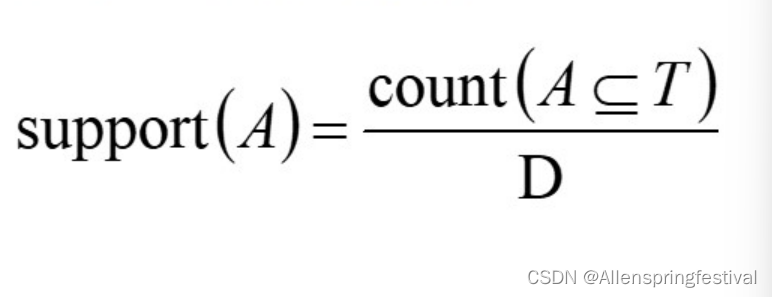
 频繁项集：支持度满足最小支持度阈值的项集称为频繁项集。通常k-项集如果满足最小支持度阈值，称为频繁集，记作Lk。

关联规则（Association Rule）:可以表示为一个蕴含式。

如：X=>Y,X和Y分别称为关联规则的前件和后件。

关联规则是否可用，需要考察他的支持度和置信度（可信度）两个指标。

 可以通过以下实例来理解：

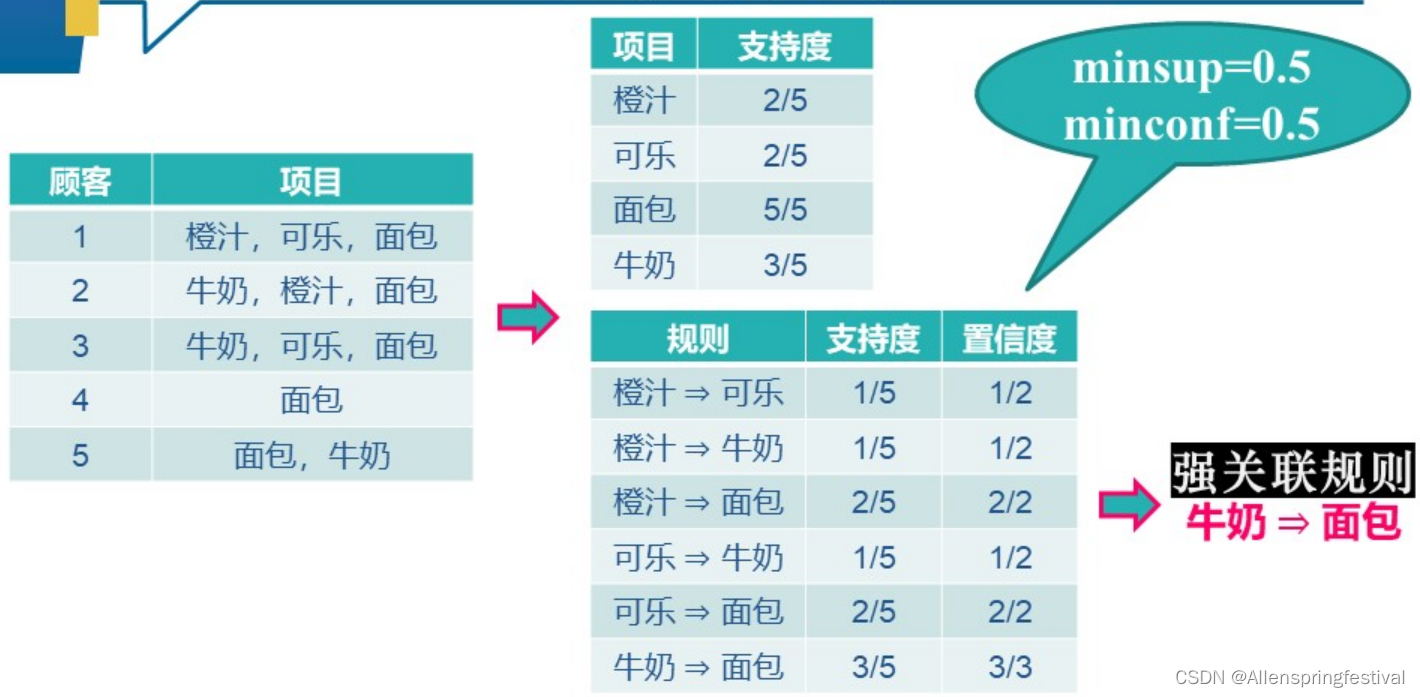
 置信度等于两者出现的支持度和前者出现的支持度之比。

 经典的Apriori关联规则算法

 Apriori关联规则算法基本思想

Apriori的基本思想：频繁项集的任何非空子集也一定是频繁的。

核心思想：扫描数据获得所有的频繁1项集L1，利用L1查找频繁2项集，如此循环直到不再有新的频繁集被找到为止。而获取不同长度的频繁项集之前，都需要先查找到候选集（支持度满足最小支持度阈值的项集）。

 如何生成候选集呢？

 先自连接再进行修剪。

这个例子非常重要，比较容易理解。

支持度（sup）就是数出在数据集D中itemset出现的次数

{1,2,3}.{1,2,3,5},{1,3,5},{2,3,5}再进行修剪，他们的子集都必须在L2里面。

去除{1，2，3}，{1，2，3，5}，{1，3，5}

得到C3{2,3,5}

Apriori算法的缺点：

多次扫描数据库，产生巨大数量的候选集，繁琐的支持度计算。

下面我们来讲解FP-Growth算法

FP-Growth算法不产生候选项集，而是采用分而治之的策略。

（1）构建FP树：压缩数据库，并将频繁项放入频繁模式树（FP树），他仍然保留项集的关联信息。

（2）从FP树中挖掘频繁项集：
1.从FP中获得条件模式基

2.利用条件模式基，构建一个条件FP树

3.根据条件FP树，进行排列组合，挖掘出频繁项。

以下示例较为简单：重点理解

 设定最小支持度为2，得到频繁集，并按照大小重新排列。

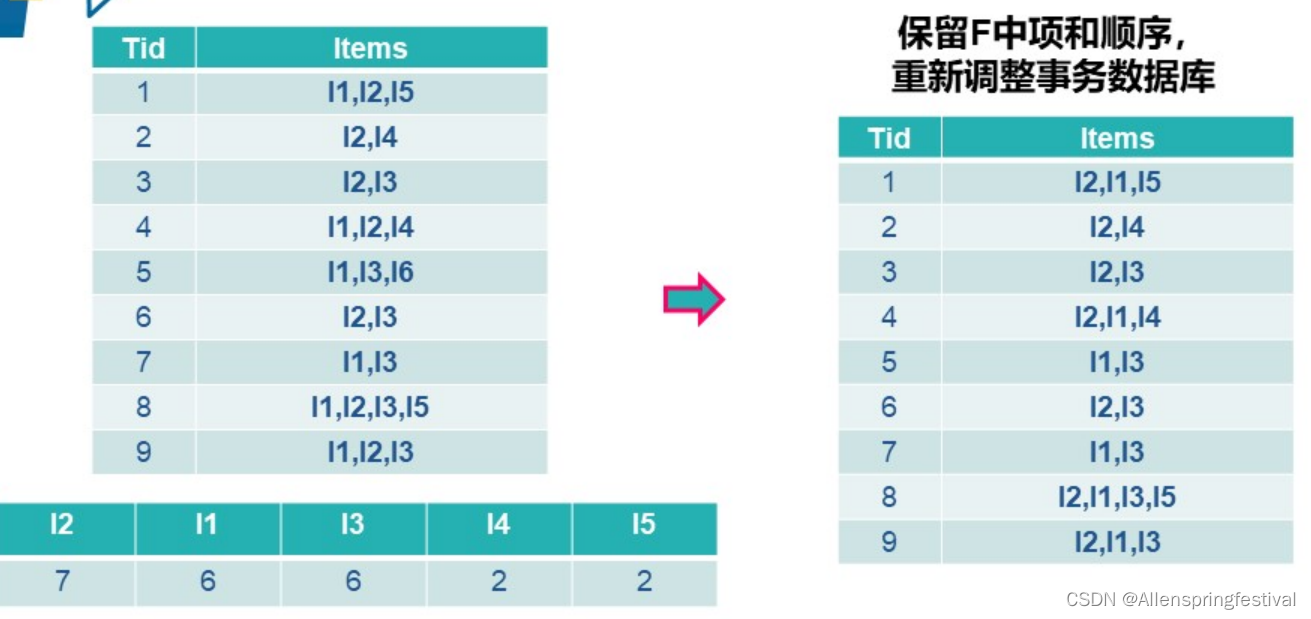
 第二次扫描排序后的数据库。并且构建FP树。

开始从FP树中进行挖掘——频繁项集

 那什么是条件模式基呢？

 为什么每个条件模式基的计数为1呢？
由于i5的计数为1，最终到达i5的重复次数也只能为1，所以条件模式基的计数是根据路径中的结点的最小计数来决定的。