当前位置：首页 > article >正文

Leetcode.1292 元素和小于等于阈值的正方形的最大边长

article 2024/12/28 2:05:43

题目链接

Leetcode.1292 元素和小于等于阈值的正方形的最大边长 Rating ： 1735

题目描述

给你一个大小为 m x n的矩阵 mat和一个整数阈值 threshold。

请你返回元素总和 小于或等于 阈值的正方形区域的最大边长；如果没有这样的正方形区域，则返回 0 。

示例 1：

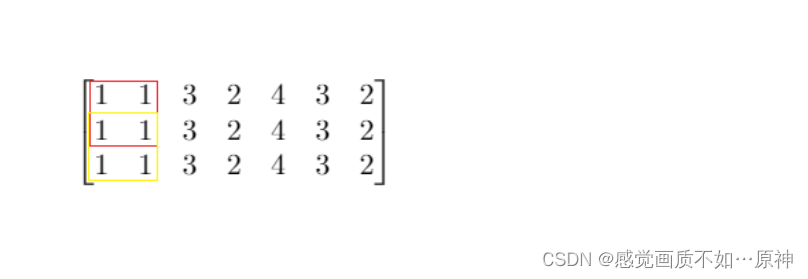
在这里插入图片描述

输入：mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
输出：2
解释：总和小于或等于 4 的正方形的最大边长为 2，如图所示。

示例 2：

输入：mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
输出：0

提示：

m == mat.length
n == mat[i].length
$1 <= m, n <= 300$
$0 <= mat[i][j] <= 10^4$
$0 <= threshold <= 10^5$

解法：二维前缀和 + 二分

首先我们将原矩阵转换为 二维前缀和矩阵s。

转换公式： $s (i, j) = s (i - 1, j) + s (i, j - 1) - s (i - 1, j - 1) + ma t (i - 1, j - 1)$

接着我们再二分边长 k，左边界 l = 1，右边界 r = min(m , n)（m和 n分别是mat的行数和列数）。

如果当前矩阵 mat中能找出边长为 k的正方形，即 l = k；否则 r = k - 1。

对于终点为 (i , j)，我们计算边长为 k的总和公式为 $s u m = s (i, j) - s (i - k, j) - s (i, j - k) + s (i - k, j - k)$

时间复杂度： $O (m * n * l o g (min (m, n))$

C++代码：


class Solution {
public:
    int maxSideLength(vector<vector<int>>& mat, int threshold) {
        int m = mat.size() , n = mat[0].size();
        vector<vector<int>> s(m+1,vector<int>(n + 1));
        for(int i = 1;i <= m;i++){
            for(int j = 1;j <= n;j++){
                s[i][j] = s[i][j-1] + s[i-1][j] - s[i-1][j-1] + mat[i-1][j-1];
            }
        }
        
        int l = 0 , r = min(m,n);
        while(l < r){
            int k = (l + r + 1)/2;
            bool ok = false;

            for(int i = k;i <= m;i++){
                for(int j = k;j <= n;j++){
                    int area = s[i][j] - s[i][j-k] - s[i-k][j] + s[i-k][j-k];
                    if(area <= threshold){
                         ok = true;
                         break;
                    }
                }
            }

            if(ok) l = k;
            else r = k - 1;
        }

        return r;
    }
};