当前位置： 首页 > article >正文

线性结构-数组

article 2024/11/13 12:41:18

数组(Array)是最简单的数据结构，是由有限个相同类型的变量或对象组成的有序集合。因为数组中各元素之间是按顺序线性排列的，所以数组是一种线性数据结构。

数组是一类物理空间和逻辑形式都连续的线性数据结构：

  • 数组用唯一的名字标识，通过数组名可以对数组中的元素进行引用。例如array[0]表示数组中的第一个元素。
  • 数组中的元素类型必须相同。
  • 数组的内存单元是连续的，一个数组要占据一个地址连续的内存空间。
  • 数组中的数据元素都是顺序存放的，元素之间有先后关系，数组元素之间不能存在空隙。

数组的定义

int[] array;
或者：
int array[];
这两种定义方式是等价的，不过第一种更符合Java的编程规范。
上面只是声明了一个引用变量array，其本质还是一个指针，而数组本身并不存在，也就是说在内存中还没有开辟那段连续的存储空间。要使用数组，必须先对数组进行初始化。

Java中初始化数组有两种方法：静态初始化和动态初始化。

静态初始化：
定义数组时显式地指定数组的初始值，系统会根据初始值的个数和类型自动为数组在堆内存中开辟空间。

//定义数组和初始化数组同时完成
int[] array1 = {1, 2, 3};
int array2[] = {1, 2, 3};
//定义数组
int[] array3;
//初始化数组
array3 = new int[] {1,2,3};

动态初始化：
在初始化数组时仅指定数组的长度，不指定数组元素的初始值。
动态初始化不会显式地为数组指定初始值，系统为会该数组指定默认的初始值。

//定义数组和初始化数组同时完成
int[] array1 = new int[3];
int array2[] = new int[3];
//定义数组
int[] array3;
//动态初始化数组，只指定数组的长度
array3 = new int[3];
System.out.println(array3[0]);//0

定义自己的数组类

如果我们希望定义更加完备的数组结构，则可以定义一个数组类，对数组地属性和操作进行封装。

public class MyArray {
	int[] array;// 数组本身
	int elemNumber; // 记录数组中元素的个数

	public MyArray(int capacity) {
		array = new int[capacity]; // 动态初始化数组，长度为capacity
		elemNumber = 0;
	}

	public boolean insertElem(int elem, int index) {
		if (index < 1 || index > elemNumber + 1) {
			System.out.println("Insert index error ");
			return false;
		}

		if (elemNumber == array.length) {
			increaseCapacity();
		}

		// 循环地将第index个元素及后面的元素都向后移动一个位置
		for (int i = elemNumber - 1; i >= index - 1; i--) {
			array[i + 1] = array[i];
		}
		// 将新元素插入到腾出的array[index-1]
		array[index - 1] = elem;
		elemNumber++;
		return true;
	}

	public boolean deleteElem(int index) {
		// 删除数组中第index位置上的元素
		if (index < 1 || index > elemNumber) {
			System.out.println("Delete index error ");
			return false;
		}
		for (int i = index; i < elemNumber; i++) {
			array[i - 1] = array[i];
		}
		elemNumber--;
		return true;
	}

	public void increaseCapacity() {
		// 增加数组的容量
		// 初始化一个新数组，容量是array容量的1.5倍
		int[] arrayTmp = new int[array.length * 2];
		System.arraycopy(array, 0, arrayTmp, 0, array.length);
		array = arrayTmp;
	}

	public void printArray() {
		for (int i = 0; i < elemNumber; i++) {
			System.out.print(array[i] + " ");
		}
		System.out.println();
	}

	public static void main(String[] args) {
		MyArray array = new MyArray(5); // 初始化一个容量为5的数组
		array.insertElem(3, 1); // 在数组的第1个位置插入3
		array.insertElem(5, 2); // 在数组的第2个位置插入5
		array.insertElem(2, 3); // 在数组的第3个位置插入2
		array.insertElem(7, 4); // 在数组的第4个位置插入7
		array.insertElem(8, 5); // 在数组的第5个位置插入8
		array.printArray(); // 打印数组内容
		array.insertElem(0, 3); // 在数组的第3个位置上插入0,需要扩容
		array.printArray(); // 打印数组内容
		array.deleteElem(7); // 企图删除第7个元素，但是删除失败
		array.printArray(); // 打印数组内容
	}
}

Myarray是我们定义的数组类，该类中包含两个成员变量：

  • array表示一个int[]类型的数组，通过array[index]的形式可以引用到数组中的元素。
  • elemNumber表示数组中元素的数量。

需要注意数组的容量和数组中元素的数量之间的区别。

  • 数组的容量指数组在堆内存中开辟的内存单元的数量，也就是上述构造函数的参数capacity所指定的大小，它表示数组中最多可以存放多少个元素。
  • 数组的中元素的数量是变量elemNumber记录的数据，它表示该数组中当前存储的有效元素的数量。

我们可以通过array.length属性获取数组的容量，所以在Myarray类中不需要定义一个变量专门记录数组的容量，但是变量elemNumber是必须的，因为数组的容量与数组中元素的数量可能不相等，这就需要通过一个变量来记录数组中有效元素的数量，否则可能从数组中取出无效值。

向数组中插入元素

public boolean insertElem(int elem, int index)
这个函数的作用是在整型数组中的第index个位置上插入一个整型元素elem。

首先要理解什么是数组的第index个位置以及什么是数组的第index个位置上插入元素。


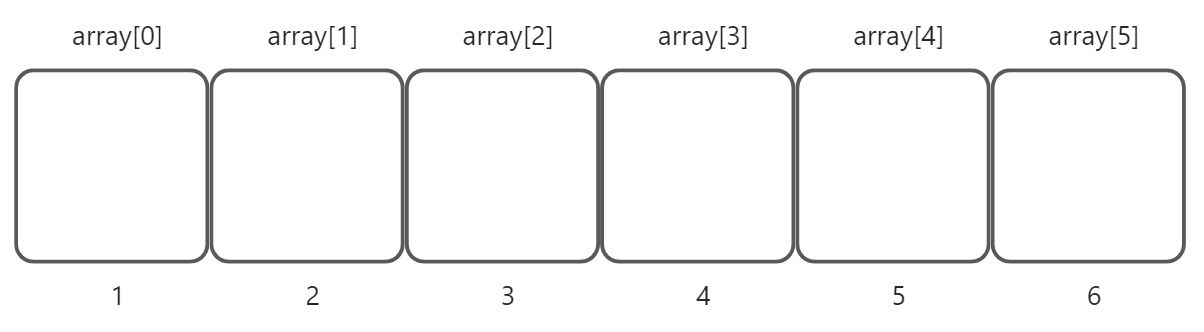
数组的第index个位置：

  • 数组中元素的位置是从1开始的，因此数组元素的下标与数组元素的位置相差1。这是一种约定俗成的规则，很多数据结构的书籍都是这样规定的。

数组的第index个位置上插入元素：

  • 就是插入的新元素要位于数组的第index个位置上，原index个位置上的元素以及后续元素都要顺序向后移动一个位置。

前面已经提到，数组的元素之间不能存在“空隙”，因此插入新元素的位置范围应为：[1,elemNumber+1]，否则数组中出现空隙，从而无法判断哪些是无有效的元素、那些是无效的。

  1. 将数组中第index个及之后的元素都向后移动一个位置，将数组的第index个位置空出来。
  2. 将新元素插入数组的第index个位置，即array[index-1]=elem;因为数组的下标与数组的位置之间相差1，所以array[index-1]就是数组的第index个元素。

需要指出的是，如果插入元素的位置是elemNumber+1，也就是在数组的最后插入一个元素，则不需要执行移动数组元素的操作，直接将元素插入数组的elemNumber+1位置即可。

public boolean insertElem(int elem, int index) {
    if (index < 1 || index > elemNumber + 1) {
        System.out.println("Insert index error ");
        return false;
    }
    // 循环地将第index个元素及后面的元素都向后移动一个位置
    for (int i = elemNumber - 1; i >= index - 1; i--) {
        array[i + 1] = array[i];
    }
    // 将新元素插入到腾出的array[index-1]
    array[index - 1] = elem;
    elemNumber++;
    return true;
}

在这段代码中，如果函数insertElem()的参数index等于elemNumber+1，则代码中循环移动元素的操作实际上是不被执行的，因为循环变量i的初始值是elemNumber-1，不满足i≥index-1=elemNumber的循环条件。
最后不要忘记elemNumber++;

数组扩容

当数组元素数量达到数组的容量上限时，就不允许再向数组中插入新元素，而是直接返回false表示插入元素失败，但是这种方法限定了数组中元素的数量，不够灵活。

我们使用动态扩容方法解决数组容量问题。
当向数组中插入元素，而数组中的元素容量又达到上限时，可以调用一个数组扩容方法对数组进行扩容，这样数组的存储空间就会随着数组元素的增多而不断增大。

public void increaseCapacity() {
    // 增加数组的容量
    // 初始化一个新数组，容量是array容量的1.5倍
    int[] arrayTmp = new int[array.length * 2];
    System.arraycopy(array, 0, arrayTmp, 0, array.length);
    array = arrayTmp;
}

这里用到了System.arraycopy()函数，具体用法请参照上面的代码。

删除元素

public boolean deleteElem(int index)
这个过程与插入元素的过程正好相反，我们只需要将第index个位置之后的元素（不含第index个位置上的元素）顺序向前移动一个位置，并将数组元素的数量减一，就可以完成删除操作。
被删除数组元素的位置只能在[1,elemNumber]的范围内，删除其他位置的元素都是非法的。
这里区间的右端点与插入时不同，插入是**elemNumber+1**。

public boolean deleteElem(int index) {
    // 删除数组中第index位置上的元素
    if (index < 1 || index > elemNumber) {
        System.out.println("Delete index error ");
        return false;
    }
    for (int i = index; i < elemNumber; i++) {
        array[i - 1] = array[i];
    }
    elemNumber--;
    return true;
}

数组的性能分析

数组适合读操作频繁，而插入删除操作较少的场景。在定义数组时，要根据实际需求指定数组大小。
如果需要扩容，则应该选择合适的扩容因子，既要尽量提高空间利用率，又要最大限度避免频繁扩容对数组性能的影响。

优点：

  • 数组是一种可随机访问的线性结构，只要给定数组名和数组的下标，就可以用 O ( 1 ) O(1) O(1)时间复杂度直接定位到对应的元素。

缺点：

  • 由于数组的元素都是顺序存储的，且数组元素之间不能存在空隙，因此在插入删除时会有大量元素移动，将严重影响效率。在数组中插入或删除一个元素的时间复杂度都是 O ( n ) O(n) O(n)级的。
  • 没有扩容功能的数组大小是固定的，在使用数组时容易出现越界的问题。增加了扩容功能的数组虽然能避免内存越界问题，但会导致内存资源的浪费，因为总有一些空闲的数组空间。

来道算法题

数组元素逆置

一个基础的双指针问题。

编写一个函数reverseArray()，将数组中元素逆置。例如原数组中的元素顺序是{1,2,3,4,5}，那么逆置后数组中的元素顺序是{5,4,3,2,1}。

数组元素的逆置操作一般要求不创建新数组，只在原数组内将数组元素的顺序颠倒过来，这样操作的效率比较高，实现起来也更加简单。
需要定义一个tmpElem作为数据缓冲区，同时要设置变量low和high，作为数组的下标分别指向数组的第1个元素和最后1个元素。然后执行以下步骤：

  1. 将low指向的元素和high指向的的元素通过临时变量tmpElem交换位置。
  2. 执行low++和high--。
  3. 重复上两个步骤直到low≥high。

对于只有一个元素的数组，以上步骤可以将该元素原地逆置，结果也是正确的。
该算法的时间复杂度为 O ( n ) O(n) O(n)，空间复杂度为 O ( 1 ) O(1) O(1)。

public void reverseArray() {
    int tmpElem;
    for (int low = 1, high = elemNumber; low < high; low++, high--) {
        // 数据交换
        tmpElem = array[low - 1];
        array[low - 1] = array[high - 1];
        array[high - 1] = tmpElem;
    }
}

删除数组中的重复元素

方法很多的一道基础算法题

编写一个purge()，删除整数数组中重复的元素。例如，数组为{1,1,3,5,2,3,1,5,6,8}，删除重复元素后数组变为{1,3,5,2,6,8}。

三重循环 O ( n 3 ) O(n^3) O(n3)

解决这个问题，最直观的方法就是用三个循环：

  1. 首先用一个循环对每个数组元素进行定位。
  2. 在用一个循环，将第一层循环定位的元素，拿来逐个对比该元素之后的每个元素。
  3. 如果发现重复，则调用deleteElem()将该元素删除。deleteElem()本身就是用一重循环来进行删除操作的。
public void purge() {
    // 两层循环分别检索数组的每个元素
    for (int i = 1; i <= elemNumber; i++) {
        for (int j = i + 1; j <= elemNumber; j++) {
            if (array[i - 1] == array[j - 1]) {
                deleteElem(j - 1);
                // 由于deleteElem本身会将后面的元素提前，所以需要修正j的位置
                j--;
            }
        }
    }
}

优化删除步骤： O ( n 2 ) + O ( n ) = O ( n 2 ) O(n^2)+O(n)=O(n^2) O(n2)+O(n)=O(n2)

上面的算法简单直观，但时间复杂度很高，为 O ( n 3 ) O(n^3) O(n3)。
我们可以在确定重复元素之后，不立刻删除该元素，而是等找到全部重复元素之后再进行整体删除。
这样就可以将 O ( n 2 ⋅ n ) = O ( n 3 ) O(n^2\cdot n)=O(n^3) O(n2⋅n)=O(n3)变为 O ( n 2 ) + O ( n ) = O ( n 2 ) O(n^2)+O(n)=O(n^2) O(n2)+O(n)=O(n2)
从而优化整体的时间复杂度。

public void purge() {
    int flag = -111;
    int i, j, number = elemNumber;
    // 两层循环确定重复元素
    for (i = 1; i < elemNumber; i++) {
        for (j = i + 1; j < elemNumber; j++) {
            if (array[i - 1] == array[j - 1]) {
                // 将重复元素填充为标记值，此处为-111
                // 由于没有执行删除操作，也就没有元素前移，不需要修正j的位置
                array[j - 1] = flag;
            }
        }
    }
    // 找到第一个特殊标记flag
    for (i = 1; array[i - 1] != flag; i++)
        ;
    for (j = i + 1; j <= number;) {
        if (array[j - 1] != flag) {
            // 如果array[j-1]不等于flag，复制j所指的有效数据复制到i标记的位置
            // i和j中间的会增加一个无效数据，这个无效数据紧挨在i之后
            // 将i和j分别后移，i指向新的无效数据，j尝试检索下一个有效数据
            array[i - 1] = array[j - 1];
            i++;
            j++;
        } else {
            // 如果array[j-1]等于flag，则j后移，寻找下一个有效数据
            j++;
        }
        // i指向当前最后一个有效数据的下一个数据，将其-1，刷新为elemNumber
        elemNumber = i - 1;
    }
}

在上面的代码中，有二重循环+一重循环+一重循环。将一重循环单独拿出来，是为了优化时间复杂度。
涉及到数组的第index个位置。需要注意元素位置和元素下标的转换。

哈希表优化查找： O ( n ) + O ( n ) = O ( n ) O(n)+O(n)=O(n) O(n)+O(n)=O(n)

使用Hashset需要导入java.util.*。
在向哈希表中添加新对象时，哈希表会判断重复对象。

  • 如果添加的对象与哈希表中已有对象重复，则添加失败，同时返回false。
  • 如果没有重复，则添加成功并返回true。

向哈希表中添加元素并查重的操作的时间复杂度仅为 O ( 1 ) O(1) O(1)。

public void purge() {
int flag = -111;
int i, j, number = elemNumber;
//使用哈希表找出数组中的重复元素
HashSet<Integer>set=new HashSet<>();
for(i=1;i<=elemNumber;i++){
    if(!set.add(array[i-1])){
        array[i-1]=flag;
    }
}
// 找到第一个特殊标记flag
for (i = 1; array[i-1] != flag; i++)
    ;
for (j = i + 1; j <= number;) {
    if (array[j - 1] != flag) {
        // 如果array[j-1]不等于flag，复制j所指的有效数据复制到i标记的位置
        // i和j中间的会增加一个无效数据，这个无效数据紧挨在i之后
        // 将i和j分别后移，i指向新的无效数据，j尝试检索下一个有效数据
        array[i - 1] = array[j - 1];
        i++;
        j++;
    } else {
        // 如果array[j-1]等于flag，则j后移，寻找下一个有效数据
        j++;
    }
    // i指向当前最后一个有效数据的下一个数据，将其-1，刷新为elemNumber
    elemNumber = i-1;
}

}

这一算法的代价就是需要用到哈希表，增加了空间复杂度。以空间换时间。


http://www.kler.cn/a/18261.html

相关文章：

  • 给查询业务添加redis缓存和缓存更新策略
  • Docker无缝更新Zentao
  • Ubuntu 的 ROS 操作系统turtlebot3环境搭建
  • 2024年【汽车修理工（高级）】考试试卷及汽车修理工（高级）证考试
  • TCP可靠连接的建立和释放，TCP报文段的格式，UDP简单介绍
  • 贪心算法-汽车加油
  • nestjs笔记
  • 打动人心的故事 | 如何利用文案在Facebook上塑造品牌形象
  • 面试整理 - 二叉排序树 c语言 及java 例子
  • 【在homeassistant的ONVIF中配置TP-Link】
  • SpringBoot启用web模拟测试（一）
  • 固态继电器的优点
  • 增强型PID-自适应-前馈-神经网络控制研究（Matlab代码实现）
  • 网页端操作提示「msg.js」库简介
  • linux实现CP指令
  • LeetCode 2432. 处理用时最长的那个任务的员工
  • 从爆火的“哇呀挖”，思考我软件开发的人生意义何在？
  • JDK17新特性之--JDK9到JDK17 String 新增的新方法
  • 53.MDL、NCNN和 TFLite比较
  • C++Primer 第一章
  • 将数据从 Oracle 加载到 Azure 的框架
  • 68元工业级双核A7,全新T113核心板震撼上市!
  • CSA发布|《洞察2022 云上数据安全与重要事项 》
  • spring-web HandlerAdapter 源码分析
  • 记录每日LeetCode 2432.处理用时最长的那个任务的员工 Java实现
  • Feign组件的使用及开发中使用方式