简单三步解决动态规划难题,记好这三步,动态规划就不难
目录
- 一、简单的一维DP
- 剑指 Offer 10- I. 斐波那契数列
- 1、三板斧解决问题
- 2、优雅的解决问题
- 剑指 Offer 63 股票的最大利润
- 1、三板斧解决问题
- 2、优雅的解决问题
- 二、进阶的二维DP
- 剑指offer47 礼物的最大价值
- 1、三板斧解决问题
- 2、优雅的解决问题
- 编辑距离
- 1、三板斧解决问题
- 2、优雅的解决问题
- 三、文末
灵感来源: https://zhuanlan.zhihu.com/p/91582909
最近实在是被动态规划伤透了脑筋,今天看到这篇文章感觉醍醐灌顶一般的突然就茅塞顿开,记好这三步,动态规划就不难了,这里开篇文章记录一下,我是如何用这个方法来刷剑指offer的动态规划题的;
当然每个题都有更好的解决方法,但是我们的思路是先用陈咬金的三板斧解决了问题再来进行优化,下面简述一下思路:
第一步: 下定义
定义要求解的问题为合适的结构,一般都是一维数组或二维数组;
第二步骤:定初值
根据题目给出的实例,确定数组的前几位的初始值;
第三步骤:找关系
根据简单的题目实例,找出数组元素之间的关系式,类似数学归纳法从简单的开始往后推导;
前两步都很简单,问题的关键在于第三步找关系,上档次一点叫找状态转移方程,low一点就是小孩子说的找规律,找到规律,根据这个规律从初始值开始往下走就能找出结果!
tip: 需要注意一些题目的限定条件,比如数组溢出等等,下面就是最简单的例子
一、简单的一维DP
剑指 Offer 10- I. 斐波那契数列
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
0<= n <=100
1、三板斧解决问题
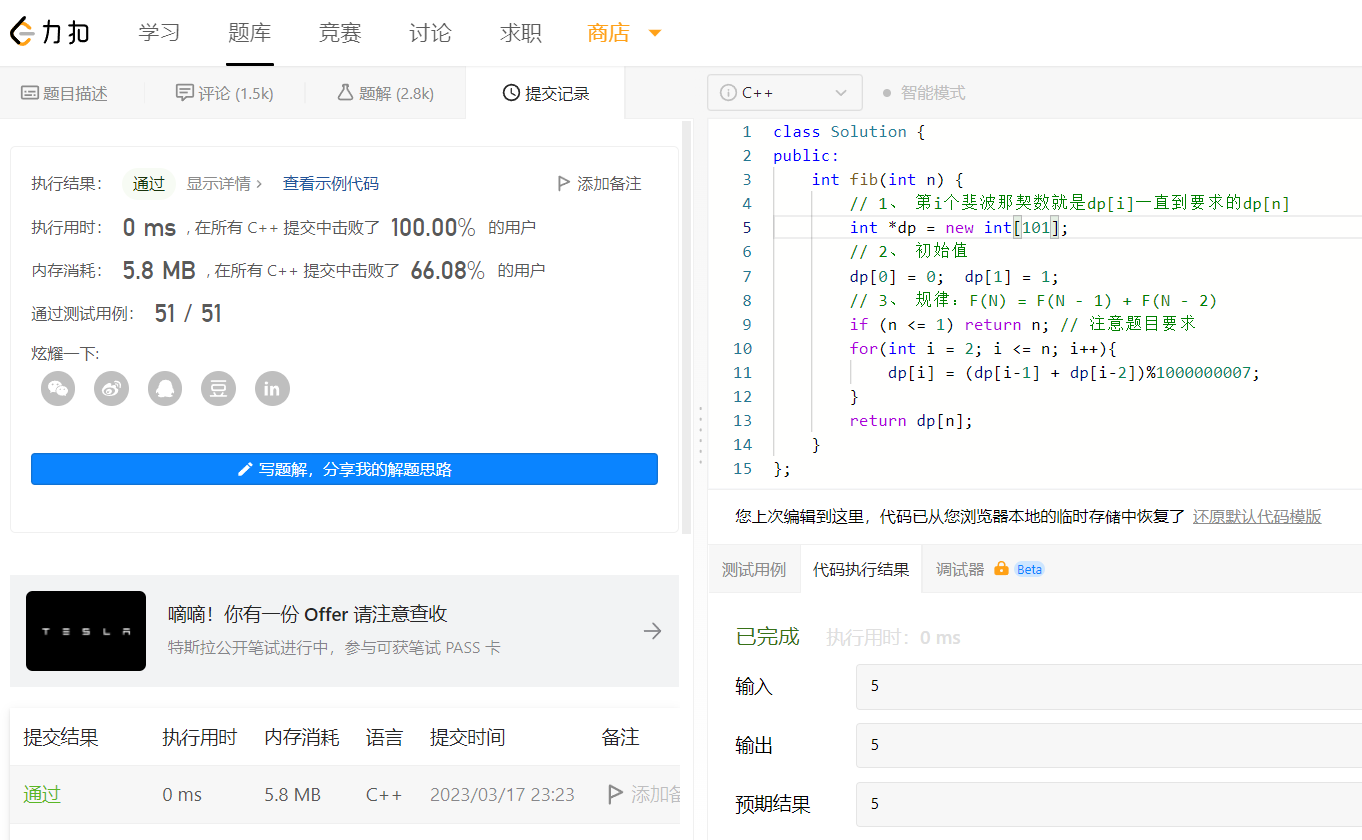
这里不会放代码,只会解释代码,要想真的弄懂还得自己去敲才行;
第一步: 下定义
要求第n的斐波那契数,就定义一个n长度的数组呗,但是这里题目提示了n最大100,所以我定义了dp[101]
第二步骤:定初值
看题目就能知道 dp[0] = 0; dp[1] = 1;
第三步骤:找关系
这个题目是直接给出来的规律F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
那就直接敲代码呗dp[i] = (dp[i-1] + dp[i-2])%1000000007; 搞定最后遍历一遍返回值就行
需要注意的细节:
注意数值溢出问题:答案需要取模 1e9+7(1000000007)
遍历需要从2开始,不然数组会越界,其实假如你注意了题目给出的 N > 1. 这个条件的话,可以忽略这条
2、优雅的解决问题
这里我们会发现,循环那个地方来来回回也就dp[i]、dp[i-1]、dp[i-2]三个变量来回的变,我们可以优化代码用三个变量来代替数组从而节省内存!
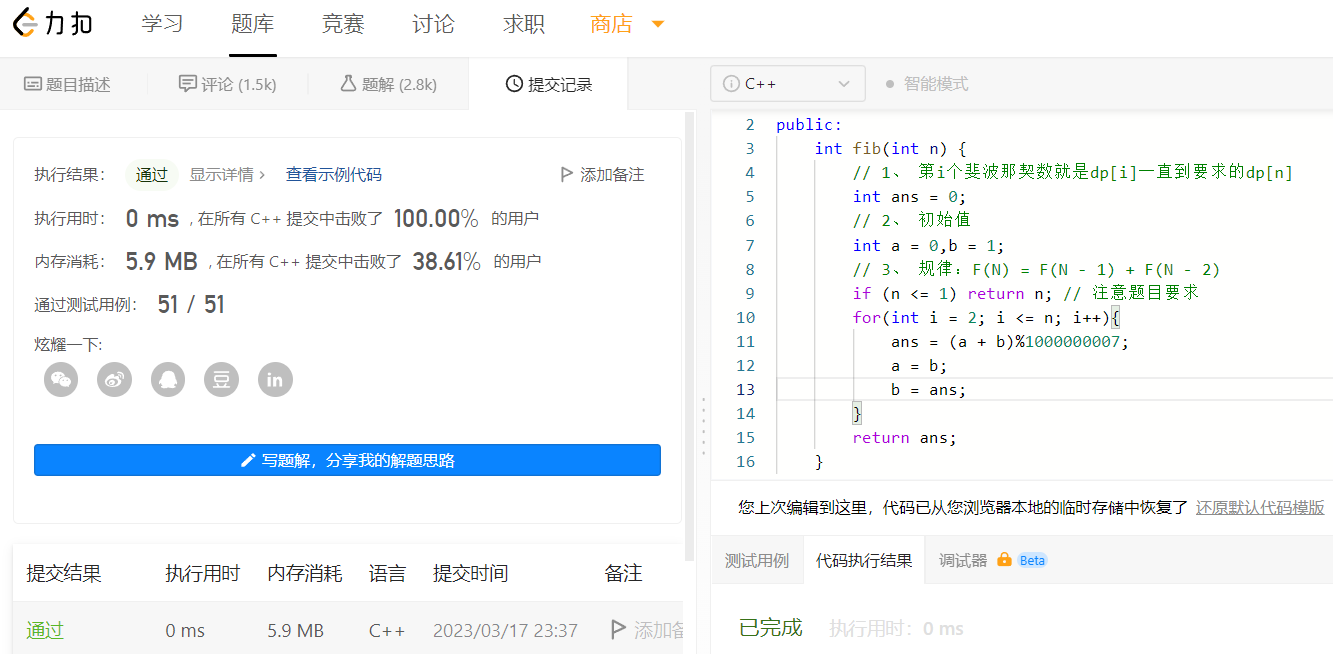
这里三板斧用的是一维数组,后来优化了空间复杂度,然鹅这只是简单的入门题目,大部分情况动态规划都是二维数组,好了思路也讲了,案例实操也讲了,用这三板斧尝试一下 青蛙跳台阶问题吧,或许你也可以优雅的解决问题,这两个题目是一样的道理,接下来讲一个规律不会直接给你而是需要自己去找的题目;
剑指 Offer 63 股票的最大利润
假设把某股票的价格按照时间先后顺序存储在数组中,请问买卖该股票一次可能获得的最大利润是多少?
示例 1:
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
示例 2:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
限制:
0 <= 数组长度 <= 10^5
1、三板斧解决问题
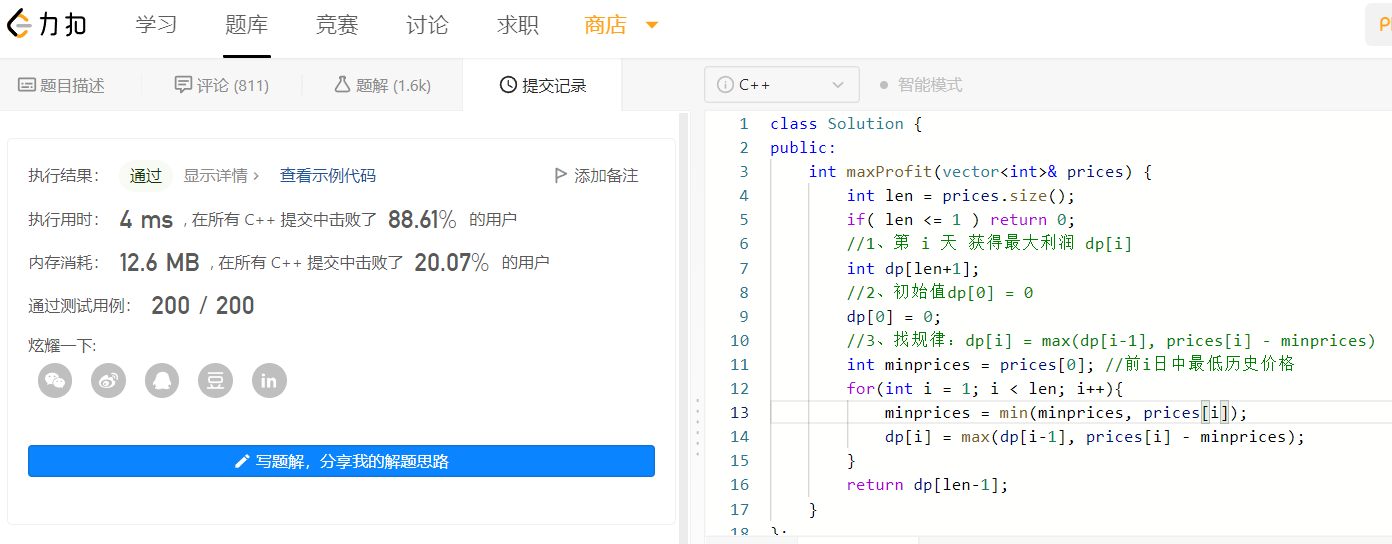
2、优雅的解决问题
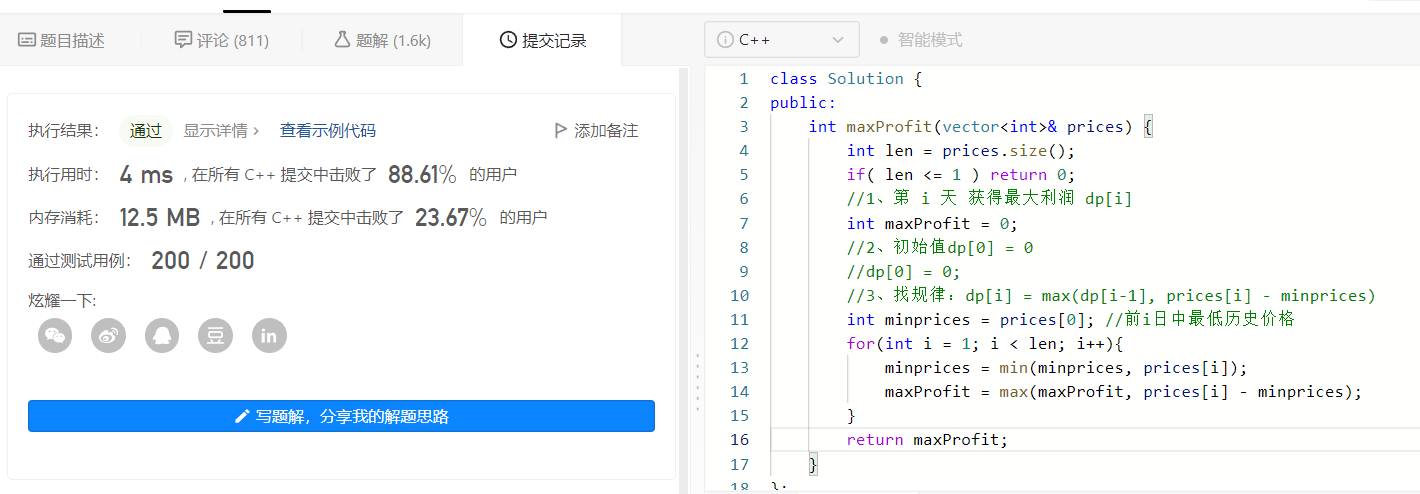
二、进阶的二维DP
剑指offer47 礼物的最大价值
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
示例 1:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物
提示:
0 < grid.length <= 200
0 < grid[0].length <= 200
1、三板斧解决问题
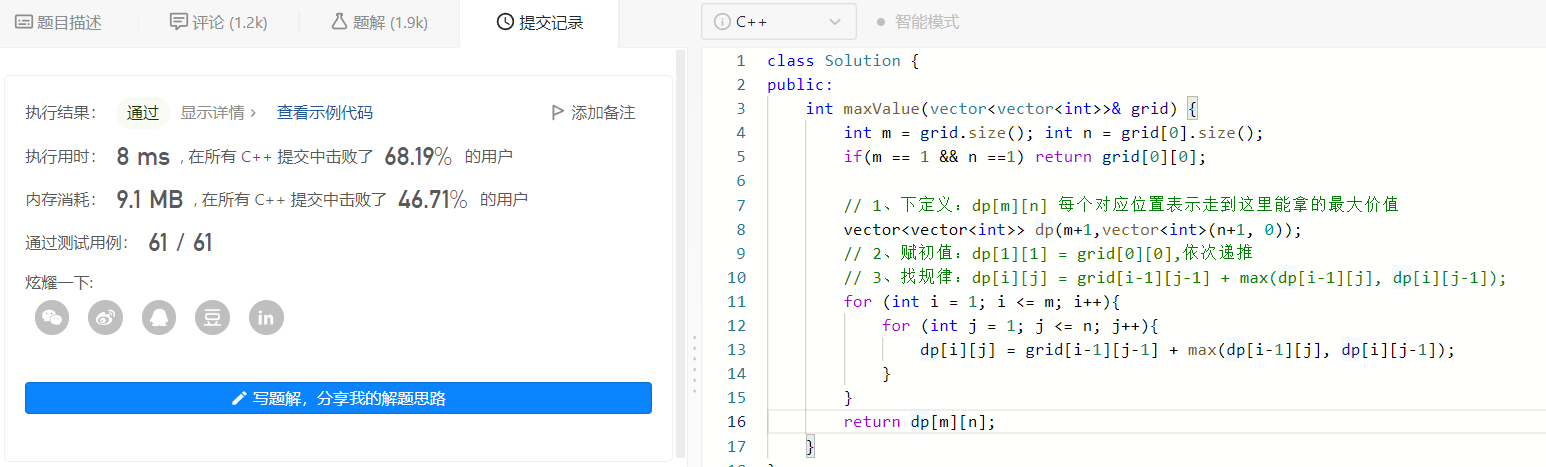
第一步: 下定义
首先必须知道最大价值的礼物一定是右下角的值,因为只能右或下移;
我们当然可以不用定义二维数组,直接在源程序上修改,但是这样毁坏了原始数据,所以我们新定义一个 dp[m+1][n+1] 的数组来表示走到棋盘对应位置的已拿的最大价值;
第二步骤:定初值
每要求一个dp[i][j]位置的值,都需要dp[i][j-1]和dp[i-1][j]中的较大的值加上这个位置本身的值,所以dp[1][1] = grid[0][0]
第三步骤:找关系
每个位置的初值为当前位置的值,加上当前位置上一行的值和左边的值中的较大值,因为当前位置的值只能是下移或者右移过来的;dp[i][j] = grid[i-1][j-1] + max(dp[i-1][j], dp[i][j-1]);
这里发现赋初值的操作可以省略,因为推导的过程一起做了、最后返回推导出的右下角的dp值就行;
注意:
1、下定义的时候如果是int dp[][]的形式要记得初始化每个元素为0,我这里直接用的stl库中的二维vector,下定义的同时初始化了每个元素为0;
2、如果不想下定义和定初值那么麻烦,可以直接在grid 数组上修改,先初始化第一列和第一行那么就能直接从 1,1的位置开始推导,但是你心里得明白推导的值的定义是什么,初始化为啥这么初始化
2、优雅的解决问题
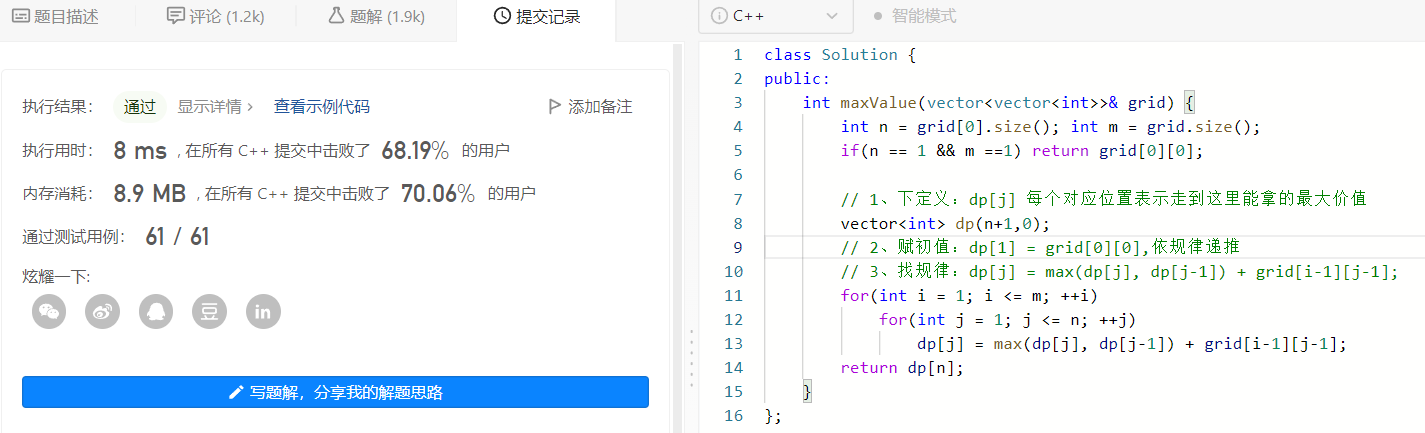
之前的一维dp中的优化问题把一维数组降阶为几个变量,这里我们把二维数组降阶为一维数组,并用它来就像滚动一样去遍历下一个值,所以叫它滚动数组。规律修改如下:
dp[j] = grid[i-1][j-1] + max(dp[j-1], dp[i-1]);
每次遍历下一行数组的值,新的dp[j]值为,旧的dp[j](当前元素的上边元素)和dp[j-1](当前元素的左边元素)中的最大值加上当前位置的礼物值;
可以这样想象一下,从左到右从上到下遍历每个位置的礼物的值的时候,有着一个滚动着的数组每次都是在你要推导的值位置的上方,它记录着假如走到滚动数组中对应棋盘的位置所能拿到的礼物最大值。 而我每次要做的其实就是不断更新滚动数组中的值,让它滚到最后一行即可;
需要注意的细节:
1、与三板斧解决问题的方法一样,每次推导一个位置的值都需要当前位置左边的值和上边的值,我们用滚动数组代替了这些值,不过三板斧时初始化是第一行和第一列置为0,这里初始化是把滚动数组置0;
2、注意数组越界问题
3、思考一下为什么不能再把滚动数组降阶成几个变量表示(注意是不能修改原数组,如果可以修改原数组那么可以不需要变量直接根据规律推导)
虽然三板斧也能解决问题,但是大部分情况下二维数组的DP都可以优化为一维的DP,最主要的就是要找出它们之间的值依赖关系,也就是规律,就算是hard难度级别的题也是如此,比如下面这题
编辑距离
题目描述
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
示例 1:
输入:word1 = “horse”, word2 = “ros”
输出:3
解释:
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)
示例 2:
输入:word1 = “intention”, word2 = “execution”
输出:5
解释:
intention -> inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)
提示:
0 <= word1.length, word2.length <= 500
word1 和 word2 由小写英文字母组成
1、三板斧解决问题
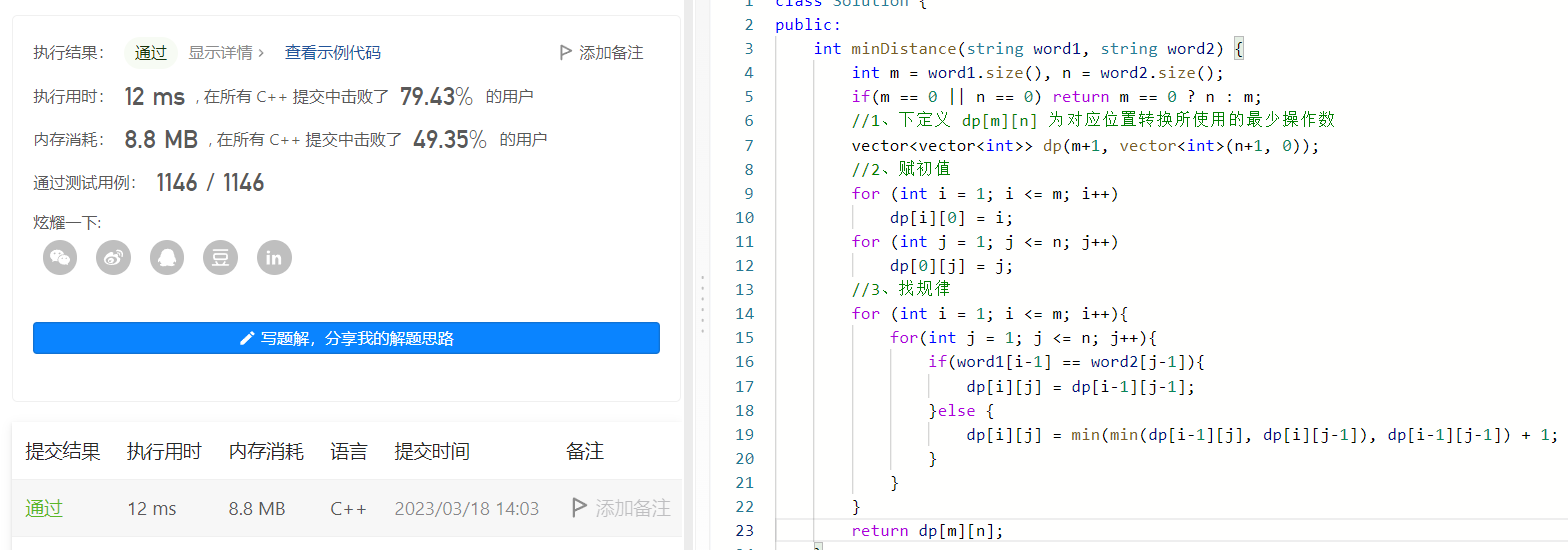
第一步: 下定义
要求将 word1 转换成 word2 所使用的最少操作数,那么就设 dp[m+1][n+1] 为 最少操作数
第二步骤:定初值
初值怎么定?看题目啊!!!重要得事情说三遍
| 解释示例 | 空 | r | o | s |
|---|---|---|---|---|
| 空 | 从空到空为0 | 从空到r 为 1 | 从空到 ro 为 2 | 从空到 ro 为 3 |
| h | 从h到空为 1 | ----- | ----- | ----- |
| o | 从ho到 空 为2 | ----- | ----- | ----- |
| r | 从hor到 空为 3 | ----- | ----- | ----- |
| s | ----- | ----- | ----- | ----- |
| e | ----- | ----- | ----- | ----- |
看一下题目最简单的例子,很轻松的初值怎么赋值我就不多说了吧(实在是懒得敲完,直接电脑跑出来看)
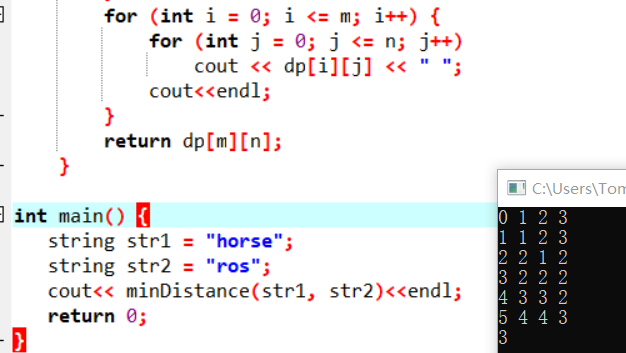
第三步骤:找关系
通过例子找规律,通过简单的推复杂的,观察一下子例子如下(省略了无用数值):
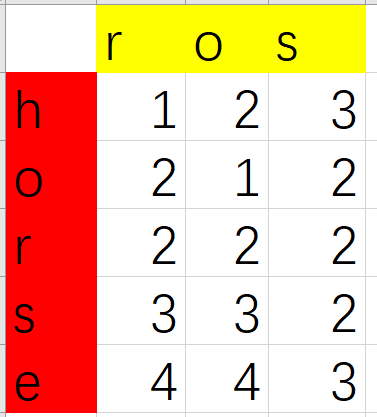
可以发现这样一种规律:
当word1[i-1] == word2[j-1] 时, dp[i][j] = dp[i-1][j-1]
当word1[i-1] != word2[j-1] 时, dp[i][j] = min( dp[i-1][j-1], dp[i-1][j] , dp[i][j-1] ) + 1
根据这个规律敲完代码就Ok了,当然了这个规律得推导过程是繁琐而漫长的,不然怎么会有一杯茶一只烟,一个题目做一天的说法
2、优雅的解决问题
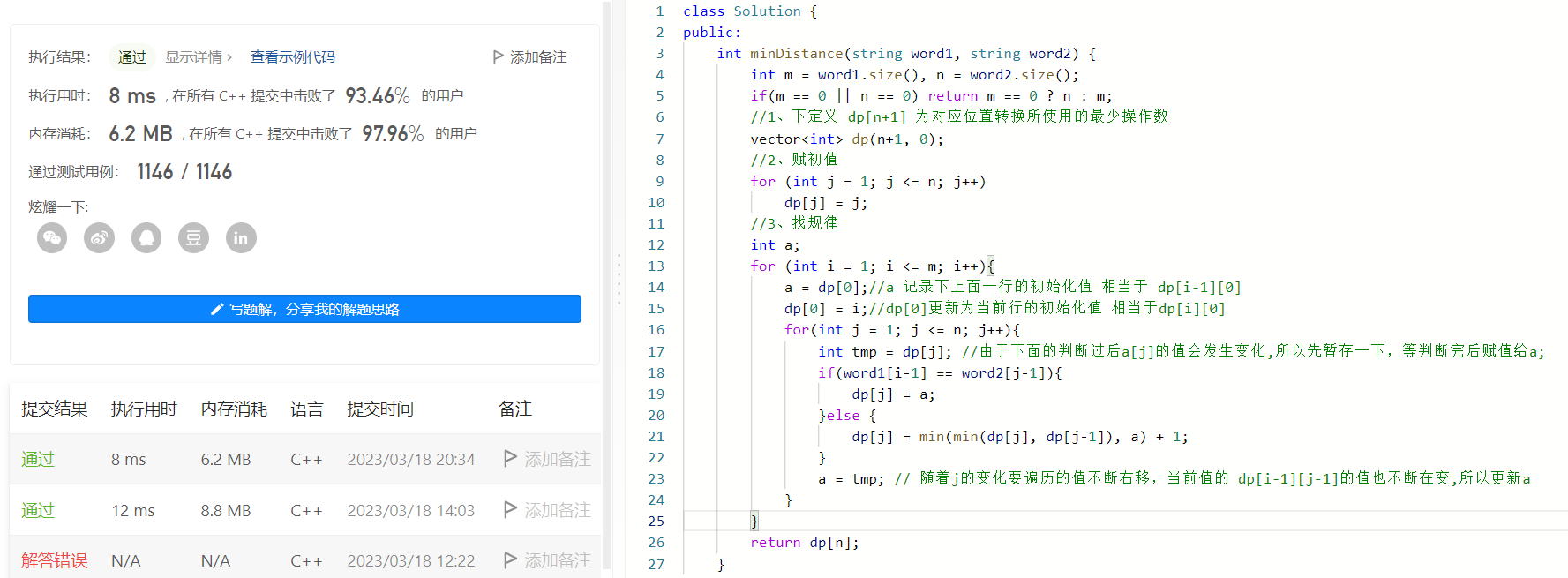
多数二维dp都可以降阶为一维dp这里也不例外,这里的降级和前面礼物的最大价值差不多也是用滚动数组,区别在于礼物的最大价值每次推导只用上、左两变量就行,而这里需要左上,上,左三变量;所以多出来的左上用a来表示,它其实就是之前的dp[i-1][j-1],然后就是要随着每一行的往右去的推导不断变化值;
注意:由于每次推导方程要用到
a,而a用完以后需要更改为下一个值的dp[i-1][j-1]也就是d[j]的原始值,但是d[j]发生了变化,所以先用个tmp存一下,推导完后赋值给a;
三、文末
算法之道,无穷无尽也,求解之道,无他,唯手熟尔! 遇到需要求什么最优,最值之类的题目且元素之间存在规律或者说联系的题目时,你应该要想的到动态规划,然后这解题三板斧下去,至少能开个头,接着就是靠简单的案例入手去找规律了,大部分情况下不是一维dp就是二维dp,先别管怎么优化做出来能把用例跑通再说优化,接着就是考虑一些细节上的问题。 以上大概就是最近所领悟的经验,如果有问题欢迎指出来评论交流,如果感觉有用的话别忘了给个赞,让我知道能够给别人带来了一点点的启发,那我就已经非常开心了。
ps : 关键在于多练哦,编辑距离这道题我起码写了3遍以上才能够独立写出来,最初看题解都是懵逼的,主要是那个规律你想要去推出来要么是你刷过类似的题目有经验,要不然就是真的天分比较好逻辑能力很强的大佬能够自己独立的把它推导出来,否则第一次谁都很难说把它做出来,所以不要灰心,你做一次不行,那就两次,过段时间忘了在像我一样第三次,第四次这样的话就可以跻身前者,之后碰到类似的也就不怕了,前进吧,少年,0和1的世界还有很多的未知等待着你,冲冲冲!!!
