前端面试拼图-数据结构与算法
摘要:总结一些前端算法题,持续更新!
一、数据结构与算法
时间复杂度-程序执行时需要的计算量(CPU)
空间复杂度-程序执行时需要的内存空间
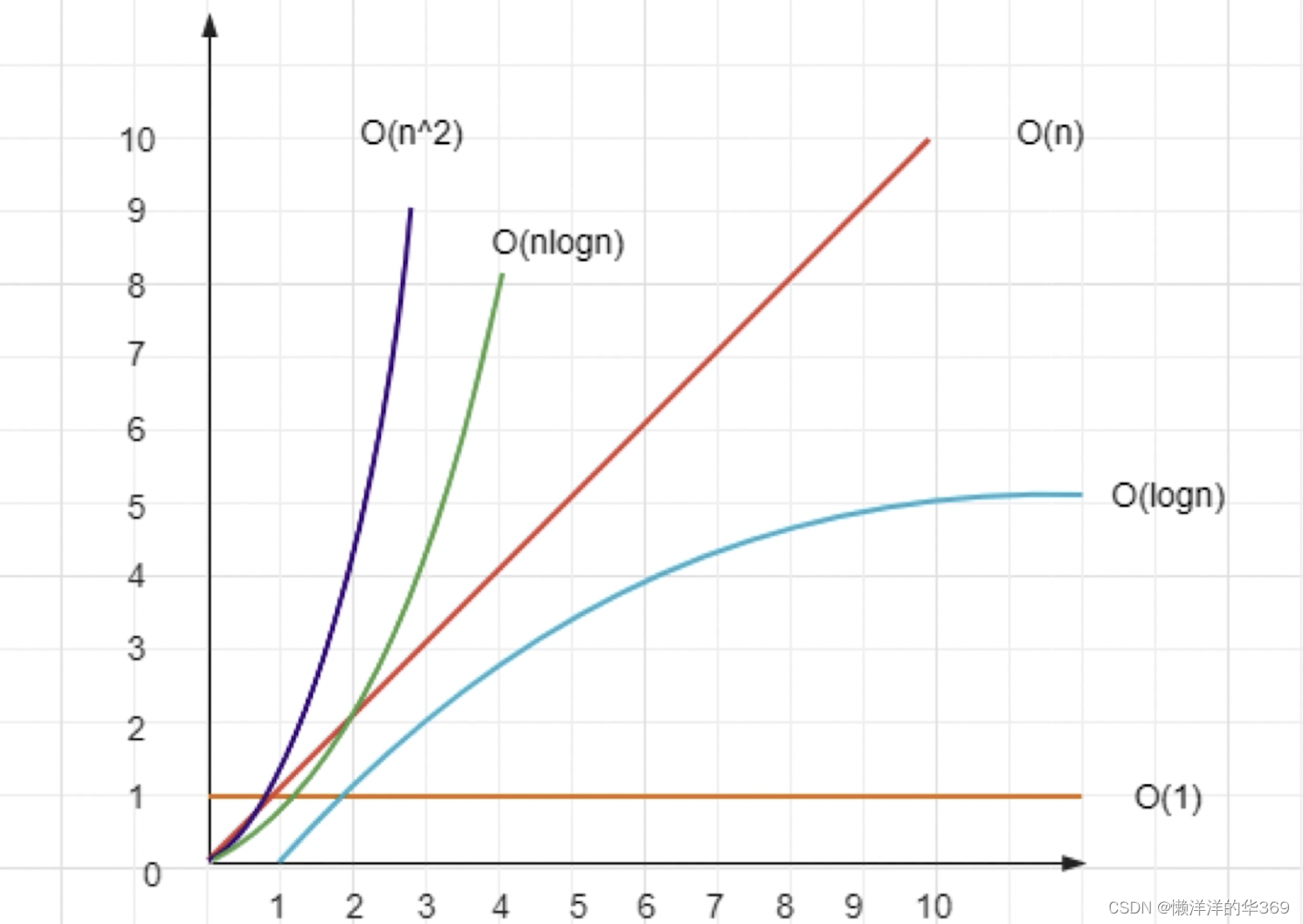
前端开发:重时间,轻空间
1.把一个数组旋转k步
array = [1, 2, 3, 4, 5, 6, 7] 旋转数组k=3, 结果[5, 6, 7, 1, 2, 3, 4]
思路1:把末尾的元素挨个pop,然后unshift到数组前面;
思路2:把数组拆分,最后concat拼接到一起
/**
* 旋转数组k步使用pop和unshift
*/
function rotate1(arr: number[], k: number): number[] {
const length = arr.length
if (!k || length === 0) return
const step = Math.abs( k%length) // abs 取绝对值,k不是数值是返回NaN
// 时间复杂度o(n^2), 空间复杂度o(1)
for (let i = 0; i<step; i++) { // 任何值与NaN做计算返回false
const n = arr.pop()
if (n != null ) {
arr.unshift(n) //数组是一个有序结构,unshift操作会非常慢!!!O(n);splice和shift也很慢
}
}
return arr
}
/**
* 旋转数组k步使用concat
*/
function rotate2(arr: number[], k: number): number[] {
const length = arr.length
if (!k || length === 0) return
const step = Math.abs( k%length) // abs 取绝对值
const part1 = arr.slice(-step) // O(1)
const part2 = arr.slice(0,length-step)
// 时间复杂度o(1), 空间复杂度O(n)
return part1.concat(part2)
}常见内置API中的复杂度:
- unshift: unshift 方法将给定的值插入到类数组对象的开头,并返回新的数组长度。时间复杂度为 O(n),其中 n 是数组的长度,因为在插入时需要将原有的元素逐一往后移动一位;空间复杂度为 O(1)。
- splice: splice 方法用于从数组中添加或删除元素,并返回被删除的元素组成的新数组。splice 的时间复杂度为 O(n),其中 n 是数组的长度,因为在删除或插入元素后,需要移动数组中的其他元素以保持连续性;空间复杂度为 O(n),因为需要创建一个新的数组。
- shift: shift 方法用于从数组的开头删除一个元素,并返回被删除的元素。shift 的时间复杂度为 O(n),其中 n 是数组的长度,因为在删除元素后,需要将数组中的其他元素往前移动一位以保持连续性;空间复杂度为 O(1),因为不需要额外的空间来存储。
- concat: concat 方法用于将两个或多个数组合并成一个新数组。时间复杂度为 O(1),数组末尾操作;空间复杂度为 O(n+m),m、n是原数组长度,因为新的数组需要存储。
- slice: slice 方法用于从数组中提取出指定范围的元素,并返回一个新数组(不改变原数组)。时间复杂度为 O(1);空间复杂度为 O(n),因为需要创建一个新的数组来存储提取的元素。
2.判断字符串是否为括号匹配
一个字符串s可能包括{}()[]三种括号,判断s是否是括号匹配
考察的数据结构是栈,先进后出;ApI: push pop length
栈 VS数组区别
栈:逻辑结构;理论模型,不管如何实现,不受任何语言限制
数组:物理结构;真实功能实现,受限于编程语言
/**
* 判断是否括号匹配
*/
function matchBracket(str: string): boolean {
const length = str.length
if(length === 0) return true
const stack = []
const leftSymbols = '{[('
const rightSymbols = '}])'
for (let i = 0; i <length; i++) {
const s = str[i]
if (leftSymbols.includes(s)) {
stack.push(s) // 左括号,压栈
} else if (rightSymbols.includes(s)) {
// 左括号,判断栈顶(是否出栈)
const top = stack[stack.length-1]
if (isMatch(top, s)) {
stack.pop
} else {
return false
}
}
}
return stack.length === 0
}
/**
* 判断左右括号是否匹配
*/
functionn isMatch(left: string, right: string): boolean {
if (left === '{' && right === '}') return true
if (left === '[' && right === ']') return true
if (left === '(' && right === ')') return true
return false
}时间复杂度O(n); 空间复杂度O(n)。
