【自然语言处理】P4 神经网络基础 - 激活函数
目录
- 激活函数
- Sigmoid
- Tanh
- ReLU
- Softmax
本节博文介绍四大激活函数,Sigmoid、Tanh、ReLU、Softmax。
激活函数
为什么深度学习需要激活函数?
博主认为,最重要的是 引入非线性。
神经网络是将众多神经元相互连接形成的网络。如果神经元没有激活函数,那么网络模型都将退化成为线性模型,从而失去了处理非线性问题的能力。非线性问题,如视觉识别、语音识别、图像识别等等。
当神经网络具有处理非线性的能力后,将会提高模型的 表达能力 以及 泛化能力:神经网络能够更有效地学习数据中的复杂模式和函数关系,更好地学习数据的通用特征,从而提高模型在数据上的表达能力和泛化能力。
此外,激活函数还可 提高训练效率,如 ReLU 因为在计算梯度时更为简单快速,可以加速神经网络的训练过程;确保网络的稳定性,防止梯度消失或爆炸等问题。
下面,博文将依次介绍四个激活函数以及其特征。
Sigmoid
Sigmoid 函数将任意实数 x 映射到 (0, 1) 区间内。数学上,Sigmoid 函数表示为:
f
(
x
)
=
1
1
+
e
−
x
f(x)=\frac {1} {1+e^{-x}}
f(x)=1+e−x1
Python Sigmoid 激活函数实现与绘图:
import torch
import matplotlib.pyplot as plt
x = torch.range(-5., 5., 0.1)
y = torch.sigmoid(x)
plt.plot(x.numpy(), y.numpy())
plt.show()
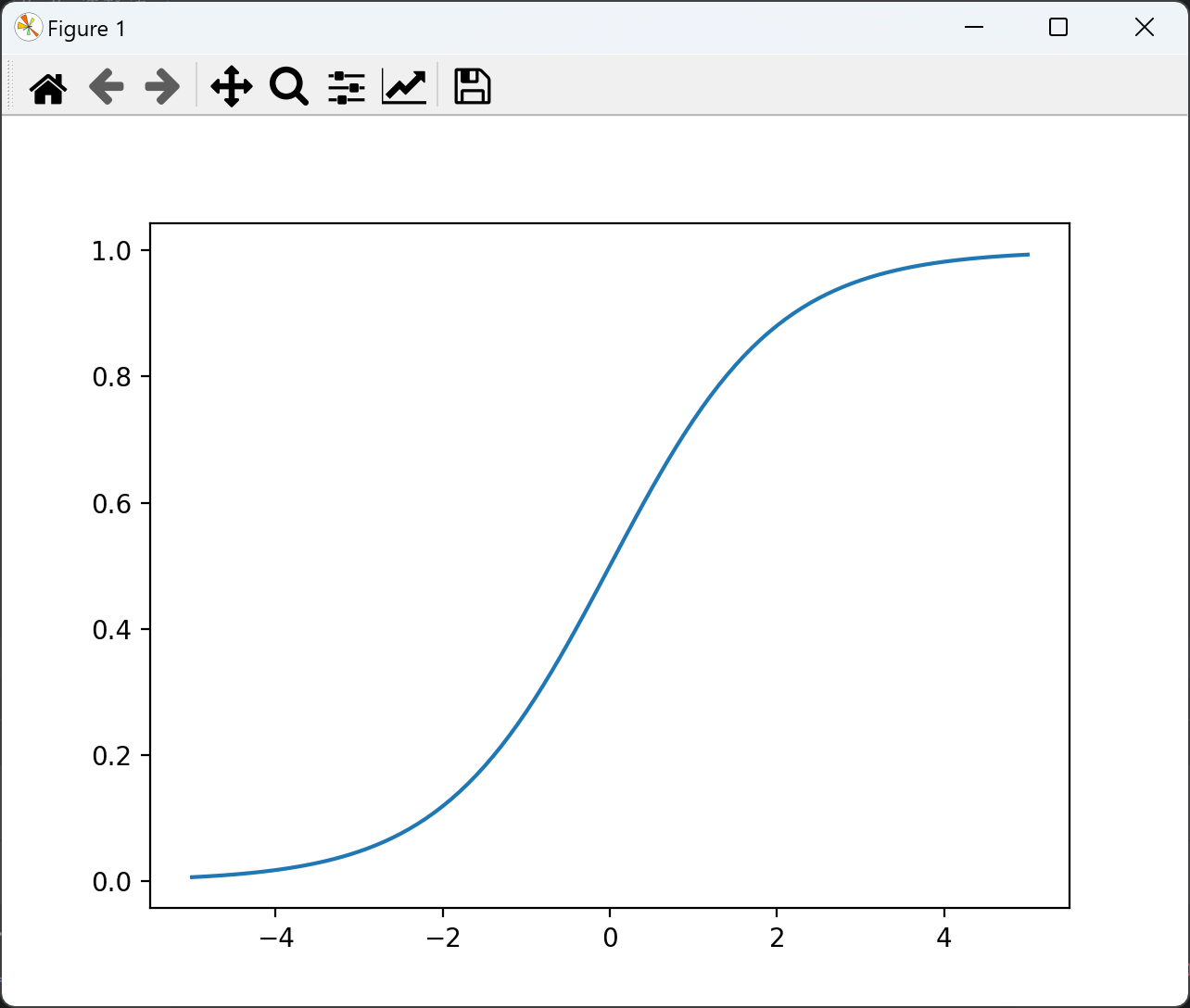
Sigmoid 函数的一些优点包括:
- 输出范围限定在 (0, 1) 之间,便于表示概率;
- 函数是连续可微的,有利于梯度的计算;
- 在二分类问题中,可以将输出值直接解读为概率。
Sigmoid 函数的一些缺点包括:
- 当输入值接近极值时,梯度会变得非常小,导致梯度消失问题,影响深层网络的训练;
- 计算量相对较大,尤其对于大规模数据集和深层网络。
Tanh
Tanh 激活函数是 Sigmoid 函数的一个变体,tanh 的函数表达式如下:
f
(
x
)
=
t
a
n
h
(
x
)
=
e
x
−
e
−
x
e
x
+
e
−
x
f(x)=tanh(x)= \frac {e^x-e^{-x}} {e^x+e^{-x}}
f(x)=tanh(x)=ex+e−xex−e−x
Python Tanh 激活函数实现与绘图:
import torch
import matplotlib.pyplot as plt
x = torch.range(-5., 5., 0.1)
y = torch.tanh(x)
plt.plot(x.numpy(), y.numpy())
plt.show()
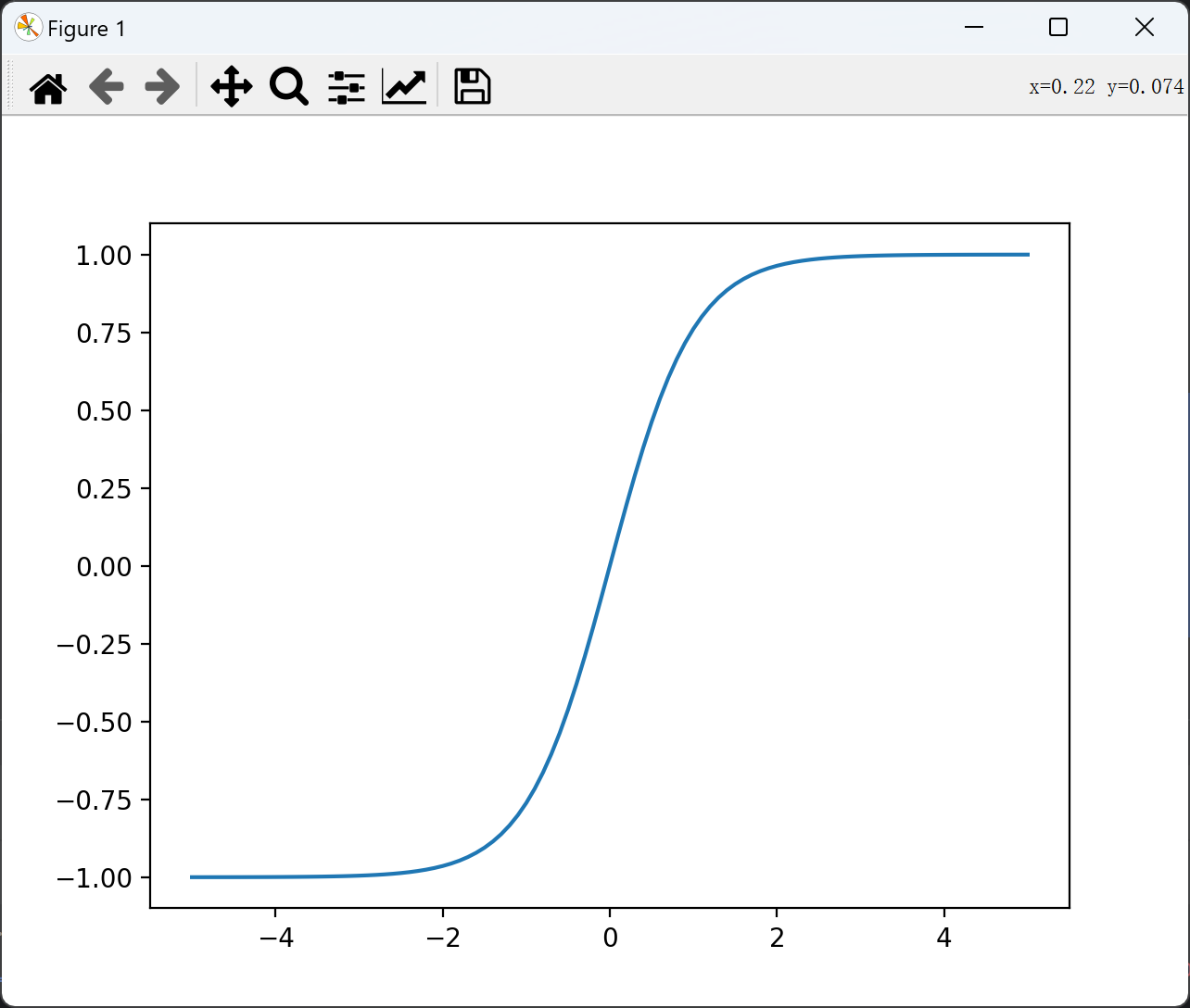
Tanh 激活函数有两个优点:
- Tanh 的输出范围为 (-1, 1),相比 sigmoid 函数的 (0, 1) 范围更广,从而使得网络可以更容易地处理梯度消失地问题;
- Tanh 在原点处的梯度为1,有助于神经网络训练过程。
Tanh 激活函数的不足:
- 当输入值很大或者很小时,Tanh 函数的梯度会变得很小,会导致训练过程中梯度消失。
在实际应用中,Tanh 函数通常用于隐藏层,而不是输出层。如果网络的输出层需要输出概率值,通常会使用 Softmax 函数而不是 Tanh。
ReLU
ReLU 激活函数是深度学习领域应用极其广泛的一种非线性激活函数。ReLU 的地位极其高,许多在深度学习领域的创新都是基于其。ReLU 函数表达式很简单,为:
f
(
x
)
=
m
a
x
(
0
,
x
)
f(x)=max(0, x)
f(x)=max(0,x)
Python ReLU 激活函数的实现与绘图:
import torch
import matplotlib.pyplot as plt
relu = torch.nn.ReLU()
x = torch.range(-5., 5., 0.1)
y = relu(x)
plt.plot(x.numpy(), y.numpy())
plt.show()
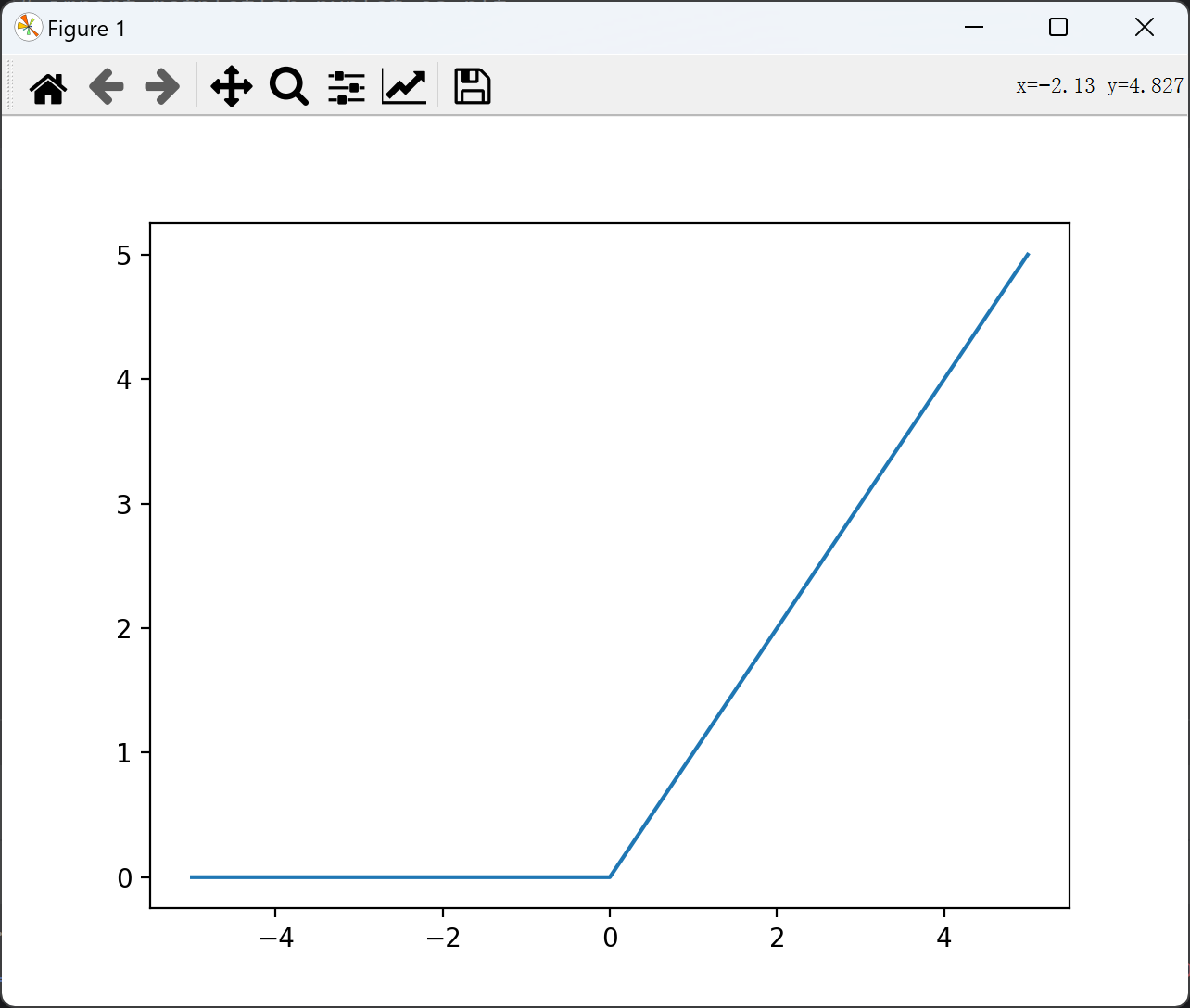
ReLU 激活函数的优点:
- 计算效率高,由于 ReLU 函数的简单性,其计算速度非常快,这使得其成为训练深度神经网络的首选激活函数;
- 缓解梯度消失问题:在传统的 Sigmoid 以及 Tanh 激活函数中,当输入值很大时,梯度会变得非常小,导致梯度消失问题。而 ReLU 激活函数在输入大于零时,梯度始终为 1,这大大减少了梯度消失的问题,使得反向传播更加有效;
- 稀疏性:ReLU 激活函数的性质使得只有少数的神经元会被激活,这对降低模型的复杂性和提高计算的效率有很大帮助;
ReLU 激活函数的缺点:
- ReLU 梯度“Death”:当输入值小于零时,对应的神经元将不会更新权重,因为梯度为零。在某些情况下,这可能会导致网络性能下降;
- Leaky ReLU 变体:为了解决 ReLU 梯度"Death" 现象,研究者提出 Leaky ReLU。其在负区间引入了一个小的斜率,这样即使输入是负的,也不会导致梯度为零。
Python Leaky ReLU 激活函数的实现与绘图:
import matplotlib.pyplot as plt
import numpy as np
# 定义PReLU函数
def prelu(x, alpha):
return np.maximum(0, x) + alpha * np.minimum(0, x)
# 设置输入值的范围
x = np.linspace(-10, 10, 100)
# 创建一个α值的列表,例如对于每个输入通道α可以是不同的
alphas = [0.1, 0.5, 1.0, 2.0]
# 绘制PReLU函数的图像
for alpha in alphas:
y = prelu(x, alpha)
plt.plot(x, y, label=f'α={alpha}')
# 添加图例
plt.legend()
# 显示图像
plt.show()
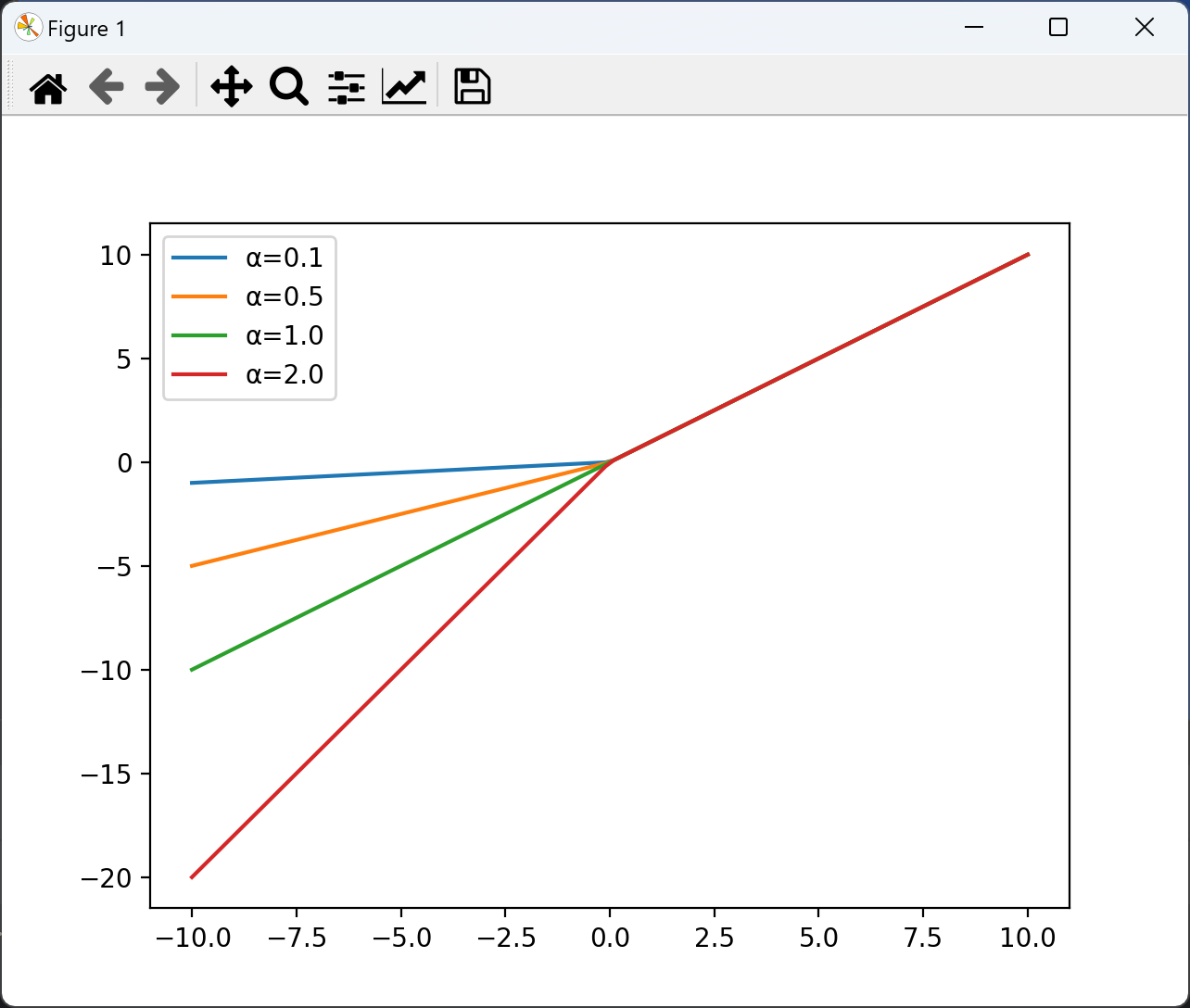
Softmax
Softmax 激活函数可以定义为一个指数函数的归一化形式。假设神经网络的输出是一个 K 维的实数向量,
z
=
[
z
1
,
z
2
,
.
.
.
,
z
k
]
z = [z_1, z_2, ..., z_k]
z=[z1,z2,...,zk],Softmax 激活函数将向量转换为一个概率分布向量,其中公式为:
s
o
f
t
m
a
x
(
z
i
)
=
e
z
i
∑
j
=
1
K
e
z
j
softmax(z_i)=\frac {e^{z_i}} {\sum ^K _{j=1} e^{z_j}}
softmax(zi)=∑j=1Kezjezi
其中 e z i e^{z_i} ezi 是 z i z_i zi 的指数,分母是所有指数的和。
Softmax 激活函数的特点:
- 概率分布:激活函数将输入向量的每个函数转化为一个概率值,表示输入属于对应类型的概率;
- 非负性:Softmax 激活函数的输出对于所有的输入都是非负的;
- 归一化:所有概率值的总和等于1,满足了概率分布的规范性要求;
Python Softmax 激活函数的实现:
# 方法一:通过 torch.nn 实现:
import torch.nn as nn
softmax = nn.Softmax(dim=1)
x = ...
y = softmax(x)
# 方法二:自己写函数:
def softmax(z):
# 防止指数运算时溢出,通过减去每行的最大值来进行数值稳定化
e_z = np.exp(z - np.max(z, axis=-1, keepdims=True))
return e_z / np.sum(e_z, axis=-1, keepdims=True)
Softmax 激活函数的优点:
- 优化梯度:Softmax 基于指数函数,所以其导数就是其本身。这使得 Softmax 在反向传播时更好地保持梯度信息,缓解梯度消失的问题。
Softmax 激活函数的缺点:
- 计算复杂性:明显,Softmax 激活函数计算相当复杂,这意味着模型输出层需要存储和计算更多的参数,导致内存占用增加;
- 训练效率:虽然 Softmax 的梯度计算相对简单,但是在反向传播过程中,由于需要计算概率分布,可能会导致训练效率的降低,尤其是在处理大量数据时;
- 局部最优:在某些情况下,Softmax 可能会导致模型陷入局部最优。
Softmax 激活函数由于其概率解释性和在多分类问题中的有效性,其虽然存在诸多潜在的缺点,但仍然是深度学习和机器学习领域广泛使用的一种激活函数。
以上便是四种激活函数的简要介绍。
如有任何疑问,欢迎读者前来探讨!
谢谢!
2024年2月4日
