七月论文审稿GPT第2.5版:微调GPT3.5 turbo 16K和llama2 13B以扩大对GPT4的优势
前言
自去年7月份我带队成立大模型项目团队以来,我司至今已有5个项目组,其中
- 第一个项目组的AIGC模特生成系统已经上线在七月官网
- 第二项目组的论文审稿GPT则将在今年3 4月份对外上线发布
- 第三项目组的RAG知识库问答第1版则在春节之前已就绪
- 至于第四、第五项目组的大模型机器人、Agent则正在迭代中
所有项目均为会对外上线发布的商用项目,而论文审稿GPT至今在过去的半年已经迭代两个版本,其中第二版的效果甚至超过了GPT4(详见《七月论文审稿GPT第2版:用一万多条paper-review数据集微调LLaMA2最终反超GPT4》),为了持续累积与原始GPT4的优势,我们如今正在迭代第2.5版本:包括对GPT3.5 turbo 16K的微调以及llama2 13B的微调,本文也因此而成
第一部分 微调GPT3.5 Tubor 16K
我们微调第一版的时候,曾经考虑过微调ChatGPT,不过其开放的微调接口的上下文长度不够大部分论文的长度(截止到23年10月底暂只有4K),故当时没来得及,好在23年11.6日,OpenAI在其举办的首届开发者大会上,宣布开放GPT3.5 16K的微调接口
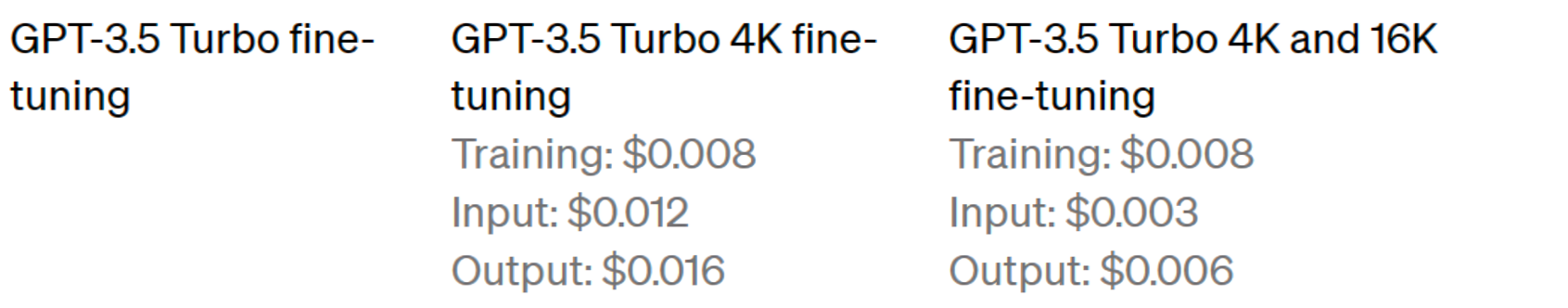
因此,我们在第2.5版便可以微调ChatGPT了,即我司正在尝试用我们自己爬取一万多条的paper-review数据集去微调GPT3.5 16k,最终让它们大乱斗,看哪个是最强王者
不过,考虑到可能存在的数据泄露给OpenAI的风险,故我们打算先用1/3的数据 微调试下,看能否把这条路径走通,以及看下胜率对比
- 如果能超过咱们微调的开源模型,那ChatGPT确实强
- 如果没超过,则再上全量
1.1 GPT3.5 Tubor 16K的微调
1.1.1 微调GPT3.5的前期调研:费用、微调流程、格式转换等
- 首先,计算一下微调GPT所需的费用
由于我司爬取的15566条paper-review数据集的token数量为:118689950
根据OpenAI微调gpt3.5 turbo的定价策略(Pricing)
可知,全量样本Traning阶段预计要花费的费用为(按2个epoch):118689950个token × 2个epoch × 0.008 × 汇率7.18 = 13635元
- 其次,这是微调的页面:https://platform.openai.com/finetune
此外,这是OpenAI官网上关于微调的教程:https://platform.openai.com/docs/guides/fine-tuning/fine-tuning-examples - 接着,根据OpenAI微调教程给的提示
把我们自己爬的数据
转成做成chatml的格式,即{"input": "[TITLE]\nImage Quality Assessment Techniques Improve Training and Evaluation of Energy-Based Generative Adversarial Networks\n\n[ABSTRACT]\nWe propose a new, multi-component energy function for energy-based Generative Adversarial Networks (GANs) based on methods from the image quality assessment literature. Our approach expands on the Boundary Equilibrium Generative Adversarial Network (BEGAN) by outlining some of the short-comings of the original energy and loss functions. We address these short-comings by incorporating an l1 score, the Gradient Magnitude Similarity score, and a chrominance score into the new energy function. We then provide a set of systematic experiments that explore its hyper-parameters. We show that each of the energy function's components is able to represent a slightly different set of features, which require their own evaluation criteria to assess whether they have been adequately learned. We show that models using the new energy function are able to produce better image representations than the BEGAN model in predicted ways.\n\n[CAPTIONS]\nFigure 1: From left to right, the images are the original image, a contrast stretched image, an image with impulsive noise contamination, and a Gaussian smoothed image. Although these images differ greatly in quality, they all have the same MSE from the original image (about 400), suggesting that MSE is a limited technique for measuring image quality.\nFigure 2: Comparison of the gradient (edges in the image) for models 11 (BEGAN) and 12 (scaled BEGAN+GMSM), where O is the original image, A is the autoencoded image, OG is the gradient of the original image, AG is the gradient of the autoencoded image, and S is the gradient magnitude similarity score for the discriminator (D) and generator (G). White equals greater similarity (better performance) and black equals lower similarity for the final column.\nFigure 3: Comparison of the chrominance for models 9 (BEGAN+GMSM+Chrom), 11 (BEGAN) and 12 (scaled BEGAN+GMSM), where O is the original image, OC is the original image in the corresponding color space, A is the autoencoded image in the color space, and S is the chrominance similarity score. I and Q indicate the (blue-red) and (green-purple) color dimensions, respectively. All images were normalized relative to their maximum value to increase luminance. Note that pink and purple approximate a similarity of 1, and green and blue approximate a similarity of 0 for I and Q dimensions, respectively. The increased gradient 'speckling' of model 12Q suggests an inverse relationship between the GMSM and chrominance distance functions.\nTable 1: Models and their corresponding model distance function parameters. The l 1 , GMSM, and Chrom parameters are their respective β d values from Equation 8.\nTable 2: Lists the models, their discriminator mean error scores, and their standard deviations for the l 1 , GMSM, and chrominance distance functions over all training epochs. Bold values show the best scores for similar models. Double lines separate sets of similar models. Values that are both bold and italic indicate the best scores overall, excluding models that suffered from modal collapse. These results suggest that model training should be customized to emphasize the relevant components.\n\n[CONTENT]\nSection Title: INTRODUCTION\n INTRODUCTION\n\nSection Title: IMPROVING LEARNED REPRESENTATIONS FOR GENERATIVE MODELING\n IMPROVING LEARNED REPRESENTATIONS FOR GENERATIVE MODELING Radford et al. (2015) demonstrated that Generative Adversarial Networks (GANs) are a good unsu- pervised technique for learning representations of images for the generative modeling of 2D images. Since then, a number of improvements have been made. First, Zhao et al. (2016) modified the error signal of the deep neural network from the original, single parameter criterion to a multi-parameter criterion using auto-encoder reconstruction loss. Berthelot et al. (2017) then further modified the loss function from a hinge loss to the Wasserstein distance between loss distributions. For each modification, the proposed changes improved the resulting output to visual inspection (see Ap- pendix A Figure 4 , Row 1 for the output of the most recent, BEGAN model). We propose a new loss function, building on the changes of the BEGAN model (called the scaled BEGAN GMSM) that further modifies the loss function to handle a broader range of image features within its internal representation.\n\nSection Title: GENERATIVE ADVERSARIAL NETWORKS\n GENERATIVE ADVERSARIAL NETWORKS Generative Adversarial Networks are a form of two-sample or hypothesis testing that uses a classi- fier, called a discriminator, to distinguish between observed (training) data and data generated by the model or generator. Training is then simplified to a competing (i.e., adversarial) objective between the discriminator and generator, where the discriminator is trained to better differentiate training from generated data, and the generator is trained to better trick the discriminator into thinking its generated data is real. The convergence of a GAN is achieved when the generator and discriminator reach a Nash equilibrium, from a game theory point of view (Zhao et al., 2016). In the original GAN specification, the task is to learn the generator's distribution p G over data x ( Goodfellow et al., 2014 ). To accomplish this, one defines a generator function G(z; θ G ), which produces an image using a noise vector z as input, and G is a differentiable function with param- eters θ G . The discriminator is then specified as a second function D(x; θ D ) that outputs a scalar representing the probability that x came from the data rather than p G . D is then trained to maxi- mize the probability of assigning the correct labels to the data and the image output of G while G is trained to minimize the probability that D assigns its output to the fake class, or 1 − D(G(z)). Although G and D can be any differentiable functions, we will only consider deep convolutional neural networks in what follows. Zhao et al. (2016) initially proposed a shift from the original single-dimensional criterion-the scalar class probability-to a multidimensional criterion by constructing D as an autoencoder. The image output by the autoencoder can then be directly compared to the output of G using one of the many standard distance functions (e.g., l 1 norm, mean square error). However, Zhao et al. (2016) also proposed a new interpretation of the underlying GAN architecture in terms of an energy-based model ( LeCun et al., 2006 ).\n\nSection Title: ENERGY-BASED GENERATIVE ADVERSARIAL NETWORKS\n ENERGY-BASED GENERATIVE ADVERSARIAL NETWORKS The basic idea of energy-based models (EBMs) is to map an input space to a single scalar or set of scalars (called its \"energy\") via the construction of a function ( LeCun et al., 2006 ). Learning in this framework modifies the energy surface such that desirable pairings get low energies while undesir- able pairings get high energies. This framework allows for the interpretation of the discriminator (D) as an energy function that lacks any explicit probabilistic interpretation (Zhao et al., 2016). In this view, the discriminator is a trainable cost function for the generator that assigns low energy val- ues to regions of high data density and high energy to the opposite. The generator is then interpreted as a trainable parameterized function that produces samples in regions assigned low energy by the discriminator. To accomplish this setup, Zhao et al. (2016) first define the discriminator's energy function as the mean square error of the reconstruction loss of the autoencoder, or: Zhao et al. (2016) then define the loss function for their discriminator using a form of margin loss. L D (x, z) = E D (x) + [m − E D (G(z))] + (2) where m is a constant and [·] + = max(0, ·). They define the loss function for their generator: The authors then prove that, if the system reaches a Nash equilibrium, then the generator will pro- duce samples that cannot be distinguished from the dataset. Problematically, simple visual inspec- tion can easily distinguish the generated images from the dataset.\n\nSection Title: DEFINING THE PROBLEM\n DEFINING THE PROBLEM It is clear that, despite the mathematical proof of Zhao et al. (2016) , humans can distinguish the images generated by energy-based models from real images. There are two direct approaches that could provide insight into this problem, both of which are outlined in the original paper. The first approach that is discussed by Zhao et al. (2016) changes Equation 2 to allow for better approxima- tions than m. The BEGAN model takes this approach. The second approach addresses Equation 1, but was only implicitly addressed when (Zhao et al., 2016) chose to change the original GAN to use the reconstruction error of an autoencoder instead of a binary logistic energy function. We chose to take the latter approach while building on the work of BEGAN. Our main contributions are as follows: • An energy-based formulation of BEGAN's solution to the visual problem. • An energy-based formulation of the problems with Equation 1. • Experiments that explore the different hyper-parameters of the new energy function. • Evaluations that provide greater detail into the learned representations of the model. • A demonstration that scaled BEGAN+GMSM can be used to generate better quality images from the CelebA dataset at 128x128 pixel resolution than the original BEGAN model in quantifiable ways.\n\nSection Title: BOUNDARY EQUILIBRIUM GENERATIVE ADVERSARIAL NETWORKS\n BOUNDARY EQUILIBRIUM GENERATIVE ADVERSARIAL NETWORKS The Boundary Equilibrium Generative Adversarial Network (BEGAN) makes a number of modi- fications to the original energy-based approach. However, the most important contribution can be summarized in its changes to Equation 2. In place of the hinge loss, Berthelot et al. (2017) use the Wasserstein distance between the autoencoder reconstruction loss distributions of G and D. They also add three new hyper-parameters in place of m: k t , λ k , and γ. Using an energy-based approach, we get the following new equation: The value of k t is then defined as: k t+1 = k t + λ k (γE D (x) − E D (G(z))) for each t (5) where k t ∈ [0, 1] is the emphasis put on E(G(z)) at training step t for the gradient of E D , λ k is the learning rate for k, and γ ∈ [0, 1]. Both Equations 2 and 4 are describing the same phenomenon: the discriminator is doing well if either 1) it is properly reconstructing the real images or 2) it is detecting errors in the reconstruction of the generated images. Equation 4 just changes how the model achieves that goal. In the original equation (Equation 2), we punish the discriminator (L D → ∞) when the generated input is doing well (E D (G(z)) → 0). In Equation 4, we reward the discriminator (L D → 0) when the generated input is doing poorly (E D (G(z)) → ∞). What is also different between Equations 2 and 4 is the way their boundaries function. In Equation 2, m only acts as a one directional boundary that removes the impact of the generated input on the discriminator if E D (G(z)) > m. In Equation 5, γE D (x) functions in a similar but more complex way by adding a dependency to E D (x). Instead of 2 conditions on either side of the boundary m, there are now four: The optimal condition is condition 1 Berthelot et al. (2017) . Thus, the BEGAN model tries to keep the energy of the generated output approaching the limit of the energy of the real images. As the latter will change over the course of learning, the resulting boundary dynamically establishes an equilibrium between the energy state of the real and generated input. It is not particularly surprising that these modifications to Equation 2 show improvements. Zhao et al. (2016) devote an appendix section to the correct selection of m and explicitly mention that the \"balance between... real and fake samples[s]\" (italics theirs) is crucial to the correct selection of m. Unsurprisingly, a dynamically updated parameter that accounts for this balance is likely to be the best instantiation of the authors' intuitions and visual inspection of the resulting output supports this (see Berthelot et al., 2017 ). We chose a slightly different approach to improving the proposed loss function by changing the original energy function (Equation 1).\n\nSection Title: FINDING A NEW ENERGY FUNCTION VIA IMAGE QUALITY ASSESSMENT\n FINDING A NEW ENERGY FUNCTION VIA IMAGE QUALITY ASSESSMENT In the original description of the energy-based approach to GANs, the energy function was defined as the mean square error (MSE) of the reconstruction loss of the autoencoder (Equation 1). Our first insight was a trivial generalization of Equation 1: E(x) = δ(D(x), x) (6) where δ is some distance function. This more general equation suggests that there are many possible distance functions that could be used to describe the reconstruction error and that the selection of δ is itself a design decision for the resulting energy and loss functions. Not surprisingly, an entire field of study exists that focuses on the construction of similar δ functions in the image domain: the field of image quality assessment (IQA). The field of IQA focuses on evaluating the quality of digital images ( Wang & Bovik, 2006 ). IQA is a rich and diverse field that merits substantial further study. However, for the sake of this paper, we want to emphasize three important findings from this field. First, distance functions like δ are called full-reference IQA (or FR-IQA) functions because the reconstruction (D(x)) has a 'true' or undistorted reference image (x) which it can be evaluated from Wang et al. (2004) . Second, IQA researchers have known for a long time that MSE is a poor indicator of image quality ( Wang & Bovik, 2006 ). And third, there are numerous other functions that are better able to indicate image quality. We explain each of these points below. One way to view the FR-IQA approach is in terms of a reference and distortion vector. In this view, an image is represented as a vector whose dimensions correspond with the pixels of the image. The reference image sets up the initial vector from the origin, which defines the original, perfect image. The distorted image is then defined as another vector defined from the origin. The vector that maps the reference image to the distorted image is called the distortion vector and FR-IQA studies how to evaluate different types of distortion vectors. In terms of our energy-based approach and Equation 6, the distortion vector is measured by δ and it defines the surface of the energy function. MSE is one of the ways to measure distortion vectors. It is based in a paradigm that views the loss of quality in an image in terms of the visibility of an error signal, which MSE quantifies. Problem- atically, it has been shown that MSE actually only defines the length of a distortion vector not its type ( Wang & Bovik, 2006 ). For any given reference image vector, there are an entire hypersphere of other image vectors that can be reached by a distortion vector of a given size (i.e., that all have the same MSE from the reference image; see Figure 1 ). A number of different measurement techniques have been created that improve upon MSE (for a review, see Chandler, 2013 ). Often these techniques are defined in terms of the similarity (S) between the reference and distorted image, where δ = 1−S. One of the most notable improvements is the Structural Similarity Index (SSIM), which measures the similarity of the luminance, contrast, and structure of the reference and distorted image using the following similarity function: 2 S(v d , v r ) = 2v d v r + C v 2 d + v 2 r + C (7) where v d is the distorted image vector, v r is the reference image vector, C is a constant, and all multiplications occur element-wise Wang & Bovik (2006) . 3 This function has a number of desirable features. It is symmetric (i.e., S(v d , v r ) = S(v r , v d ), bounded by 1 (and 0 for x > 0), and it has a unique maximum of 1 only when v d = v r . Although we chose not to use SSIM as our energy function (δ) as it can only handle black-and-white images, its similarity function (Equation 7) informs our chosen technique. The above discussion provides some insights into why visual inspection fails to show this correspon- dence between real and generated output of the resulting models, even though Zhao et al. (2016) proved that the generator should produce samples that cannot be distinguished from the dataset. The original proof by Zhao et al. (2016) did not account for Equation 1. Thus, when Zhao et al. (2016) show that their generated output should be indistinguishable from real images, what they are actu- ally showing is that it should be indistinguishable from the real images plus some residual distortion vector described by δ. Yet, we have just shown that MSE (the author's chosen δ) can only constrain the length of the distortion vector, not its type. Consequently, it is entirely possible for two systems using MSE for δ to have both reached a Nash equilibrium, have the same energy distribution, and yet have radically different internal representations of the learned images. The energy function is as important as the loss function for defining the data distribution.\n\nSection Title: A NEW ENERGY FUNCTION\n A NEW ENERGY FUNCTION Rather than assume that any one distance function would suffice to represent all of the various features of real images, we chose to use a multi-component approach for defining δ. In place of the luminance, contrast, and structural similarity of SSIM, we chose to evaluate the l 1 norm, the gradient magnitude similarity score (GMS), and a chrominance similarity score (Chrom). We outline the latter two in more detail below. The GMS score and chrom scores derive from an FR-IQA model called the color Quality Score (cQS; Gupta et al., 2017 ). The cQS uses GMS and chrom as its two components. First, it converts images to the YIQ color space model. In this model, the three channels correspond to the luminance information (Y) and the chrominance information (I and Q). Second, GMS is used to evaluate the local gradients across the reference and distorted images on the luminance dimension in order to compare their edges. This is performed by convolving a 3 × 3 Sobel filter in both the horizontal and vertical directions of each image to get the corresponding gradients. The horizontal and vertical gradients are then collapsed to the gradient magnitude of each image using the Euclidean distance. 4 The similarity between the gradient magnitudes of the reference and distorted image are then com- pared using Equation 7. Third, Equation 7 is used to directly compute the similarity between the I and Q color dimensions of each image. The mean is then taken of the GMS score (resulting in the GMSM score) and the combined I and Q scores (resulting in the Chrom score). In order to experimentally evaluate how each of the different components contribute to the underly- ing image representations, we defined the following, multi-component energy function: E D = δ∈D δ(D(x), x)β d δ∈D β d (8) where β d is the weight that determines the proportion of each δ to include for a given model, and D includes the l 1 norm, GMSM, and the chrominance part of cQS as individual δs. In what follows, we experimentally evaluate each of the energy function components(β) and some of their combinations.\n\nSection Title: EXPERIMENTS\n EXPERIMENTS\n\nSection Title: METHOD\n METHOD We conducted extensive quantitative and qualitative evaluation on the CelebA dataset of face images Liu et al. (2015) . This dataset has been used frequently in the past for evaluating GANs Radford et al. (2015) ; Zhao et al. (2016) ; Chen et al. (2016) ; Liu & Tuzel (2016) . We evaluated 12 different models in a number of combinations (see Table 1 ). They are as follows. Models 1, 7, and 11 are the original BEGAN model. Models 2 and 3 only use the GMSM and chrominance distance functions, respectively. Models 4 and 8 are the BEGAN model plus GMSM. Models 5 and 9 use all three Under review as a conference paper at ICLR 2018 distance functions (BEGAN+GMSM+Chrom). Models 6, 10, and 12 use a 'scaled' BEGAN model (β l1 = 2) with GMSM. All models with different model numbers but the same β d values differ in their γ values or the output image size.\n\nSection Title: SETUP\n SETUP All of the models we evaluate in this paper are based on the architecture of the BEGAN model Berthelot et al. (2017) . 5 We trained the models using Adam with a batch size of 16, β 1 of 0.9, β 2 of 0.999, and an initial learning rate of 0.00008, which decayed by a factor of 2 every 100,000 epochs. Parameters k t and k 0 were set at 0.001 and 0, respectively (see Equation 5). The γ parameter was set relative to the model (see Table 1 ). Most of our experiments were performed on 64 × 64 pixel images with a single set of tests run on 128 × 128 images. The number of convolution layers were 3 and 4, respectively, with a constant down-sampled size of 8 × 8. We found that the original size of 64 for the input vector (N z ) and hidden state (N h ) resulted in modal collapse for the models using GMSM. However, we found that this was fixed by increasing the input size to 128 and 256 for the 64 and 128 pixel images, respectively. We used N z = 128 for all models except 12 (scaled BEGAN+GMSM), which used 256. N z always equaled N h in all experiments. Models 2-3 were run for 18,000 epochs, 1 and 4-10 were run for 100,000 epochs, and 11-12 were run for 300,000 epochs. Models 2-4 suffered from modal collapse immediately and 5 (BE- GAN+GMSM+Chrom) collapsed around epoch 65,000 (see Appendix A Figure 4 rows 2-5).\n\nSection Title: EVALUATIONS\n EVALUATIONS We performed two evaluations. First, to evaluate whether and to what extent the models were able to capture the relevant properties of each associated distance function, we compared the mean and standard deviation of the error scores. We calculated them for each distance function over all epochs of all models. We chose to use the mean rather than the minimum score as we were interested in how each model performs as a whole, rather than at some specific epoch. All calculations use the distance, or one minus the corresponding similarity score, for both the gradient magnitude and chrominance values. Reduced pixelation is an artifact of the intensive scaling for image presentation (up to 4×). All images in the qualitative evaluations were upscaled from their original sizes using cubic image sampling so that they can be viewed at larger sizes. Consequently, the apparent smoothness of the scaled images is not a property of the model.\n\nSection Title: RESULTS\n RESULTS GANs are used to generate different types of images. Which image components are important depends on the domain of these images. Our results suggest that models used in any particular GAN application should be customized to emphasize the relevant components-there is not a one-size- fits-all component choice. We discuss the results of our four evaluations below.\n\nSection Title: MEANS AND STANDARD DEVIATIONS OF ERROR SCORES\n MEANS AND STANDARD DEVIATIONS OF ERROR SCORES Results were as expected: the three different distance functions captured different features of the underlying image representations. We compared all of the models in terms of their means and standard deviations of the error score of the associated distance functions (see Table 2 ). In particular, each of models 1-3 only used one of the distance functions and had the lowest error for the associated function (e.g., model 2 was trained with GMSM and has the lowest GMSM error score). Models 4-6 expanded on the first three models by examining the distance functions in different combinations. Model 5 (BEGAN+GMSM+Chrom) had the lowest chrominance error score and Model 6 (scaled BEGAN+GMSM) had the lowest scores for l 1 and GMSM of any model using a γ of 0.5. For the models with γ set at 0.7, models 7-9 showed similar results to the previous scores. Model 8 (BEGAN+GMSM) scored the lowest GMSM score overall and model 9 (BEGAN+GMSM+Chrom) scored the lowest chrominance score of the models that did not suffer from modal collapse. For the two models that were trained to generate 128 × 128 pixel images, model 12 (scaled BE- GAN+GMSM) had the lowest error scores for l 1 and GMSM, and model 11 (BEGAN) had the lowest score for chrominance. Model 12 had the lowest l 1 score, overall.\n\nSection Title: VISUAL COMPARISON OF SIMILARITY SCORES\n VISUAL COMPARISON OF SIMILARITY SCORES Subjective visual comparison of the gradient magnitudes in column S of Figure 2 shows there are more black pixels for model 11 (row 11D) when comparing real images before and after autoencod- ing. This indicates a lower similarity in the autoencoder. Model 12 (row 12D) has a higher similarity between the original and autoencoded real images as indicated by fewer black pixels. This pattern continues for the generator output (rows 11G and 12G), but with greater similarity between the gra- dients of the original and autoencoded images than the real images (i.e., fewer black pixels overall). The visual comparison of chrominance and related similarity score also weakly supported our hy- potheses (see Figure 3 ). All of the models show a strong ability to capture the I dimension (blue-red) of the YIQ color space, but only model 9 (BEGAN+GMSM+Chrom) is able to accurately capture the relevant information in the Q dimension (green-purple).\n\nSection Title: OUTLOOK\n OUTLOOK We bring an energy-based formulation to the BEGAN model and some of the problems of the en- ergy function originally proposed in Zhao et al. (2016) . We proposed a new, multi-component energy function on the basis of research from the Image Quality Assessment literature. The scaled BEGAN+GMSM model produces better image representations than its competitors in ways that can be measured using subjective evaluations of the associated features (e.g., luminance gradient simi- larity, chrominance similarity). For future work, we would like to extend this research to encompass other datasets and FR-IQA energy functions.\n\nSection Title: Annex Figures\n Annex Figures fig_3 Figure 4: Figure 4: Four outputs of each of the generators of all 12 models. The best images for each model were hand-picked. The first row is model 1, which corresponds with the original BEGAN model. Rows 2-12 represent our experiments. Each cell represents the output of a random sample. \n", "output": "[Significance and novelty]\n<Incremental nature of the paper> Reviewers highlighted that the paper's proposed approach was somewhat incremental, and its significance and novelty were questioned. The modifications and additions to the existing BEGAN framework were not perceived as significantly contributing to the field.\n<Limited novelty of energy function components> The paper's novelty was deemed to be restricted, particularly in the choice and justification of the energy function components. Reviewers pointed out that the selected components were borrowed from existing image quality assessment techniques, and their application was not seen as a significant contribution to GAN theories or algorithm designs.\n\n[Potential reasons for acceptance]\n<No related terms> -\n\n[Potential reasons for rejection]\n<Weak experiments and results analysis> Reviewers noted that the experimental section was weak, with reliance on visual evaluations and a limited range of datasets (primarily CelebA). This led to concerns about the thoroughness and robustness of the paper's findings.\n<Unclear significance and contribution> The paper was criticized for its lack of clarity in motivating its contributions and presenting results. Reviewers found it difficult to estimate the significance of the proposed model and understand how its results differed from baseline models.\n\n[Suggestions for improvement]\n<Broaden experimental testing> To strengthen the paper, reviewers suggested broadening the experimental testing to include different datasets involving natural images, beyond the single CelebA dataset. This would provide a more comprehensive evaluation of the proposed techniques.\n<Clarify and justify design choices> Improvements in the paper's clarity and justification were recommended, specifically in clarifying the design choices made for the energy function components. Providing clear justifications for the modifications and additions to the BEGAN framework would enhance the paper's credibility and significance.\n\n"} {"input": "[TITLE]\nOn Unifying Deep Generative Models\n\n[ABSTRACT]\nDeep generative models have achieved impressive success in recent years. Generative Adversarial Networks (GANs) and Variational Autoencoders (VAEs), as powerful frameworks for deep generative model learning, have largely been considered as two distinct paradigms and received extensive independent studies respectively. This paper aims to establish formal connections between GANs and VAEs through a new formulation of them. We interpret sample generation in GANs as performing posterior inference, and show that GANs and VAEs involve minimizing KL divergences of respective posterior and inference distributions with opposite directions, extending the two learning phases of classic wake-sleep algorithm, respectively. The unified view provides a powerful tool to analyze a diverse set of existing model variants, and enables to transfer techniques across research lines in a principled way. For example, we apply the importance weighting method in VAE literatures for improved GAN learning, and enhance VAEs with an adversarial mechanism that leverages generated samples. Experiments show generality and effectiveness of the transfered techniques. \n\n[CAPTIONS]\nFigure 1: (a) Conventional view of ADA. To make direct correspondence to GANs, we use z to denote the data and x the feature. Subscripts src and tgt denote source and target domains, respectively. (b) Conventional view of GANs. (c) Schematic graphical model of both ADA and GANs (Eq.3). Arrows with solid lines denote generative process; arrows with dashed lines denote inference; hollow arrows denote deterministic transformation leading to implicit distributions; and blue arrows denote adversarial mechanism that involves respective conditional distribution q and its reverse q r , e.g., q(y|x) and q r (y|x) (denoted as q (r) (y|x) for short). Note that in GANs we have interpreted x as latent variable and (z, y) as visible. (d) InfoGAN (Eq.9), which, compared to GANs, adds conditional generation of code z with distribution qη(z|x, y). (e) VAEs (Eq.12), which is obtained by swapping the generation and inference processes of InfoGAN, i.e., in terms of the schematic graphical model, swapping solid-line arrows (generative process) and dashed-line arrows (inference) of (d).\nFigure 2: One optimization step of the parameter θ through Eq.(6) at point θ0. The posterior q r (x|y) is a mixture of p θ 0 (x|y = 0) (blue) and p θ 0 (x|y = 1) (red in the left panel) with the mixing weights induced from q r φ 0 (y|x). Minimizing the KLD drives p θ (x|y = 0) towards the respective mixture q r (x|y = 0) (green), resulting in a new state where p θ new (x|y = 0) = pg θ new (x) (red in the right panel) gets closer to p θ 0 (x|y = 1) = p data (x). Due to the asymmetry of KLD, pg θ new (x) missed the smaller mode of the mixture q r (x|y = 0) which is a mode of p data (x).\nFigure 3: Symmetric view of generation and inference. There is little difference of the two processes in terms of formulation: with implicit distribution modeling, both processes only need to perform simulation through black-box neural transformations between the latent and visible spaces.\nTable 1: Correspondence between different approaches in the proposed formulation. The label \"[G]\" in bold indicates the respective component is involved in the generative process within our interpretation, while \"[I]\" indicates inference process. This is also expressed in the schematic graphical models in Figure 1.\nTable 2: Left: Inception scores of GANs and the importance weighted extension. Middle: Classification accuracy of the generations by conditional GANs and the IW extension. Right: Classification accuracy of semi-supervised VAEs and the AA extension on MNIST test set, with 1% and 10% real labeled training data.\nTable 3: Variational lower bounds on MNIST test set, trained on 1%, 10%, and 100% training data, respectively.\n\n[CONTENT]\nSection Title: INTRODUCTION\n INTRODUCTION Deep generative models define distributions over a set of variables organized in multiple layers. Early forms of such models dated back to works on hierarchical Bayesian models (Neal, 1992) and neural network models such as Helmholtz machines (Dayan et al., 1995), originally studied in the context of unsupervised learning, latent space modeling, etc. Such models are usually trained via an EM style framework, using either a variational inference (Jordan et al., 1999) or a data augmentation (Tanner & Wong, 1987) algorithm. Of particular relevance to this paper is the classic wake-sleep algorithm dates by Hinton et al. (1995) for training Helmholtz machines, as it explored an idea of minimizing a pair of KL divergences in opposite directions of the posterior and its approximation. In recent years there has been a resurgence of interests in deep generative modeling. The emerging approaches, including Variational Autoencoders (VAEs) (Kingma & Welling, 2013), Generative Adversarial Networks (GANs) (Goodfellow et al., 2014), Generative Moment Matching Networks (GMMNs) (Li et al., 2015; Dziugaite et al., 2015), auto-regressive neural networks (Larochelle & Murray, 2011; Oord et al., 2016), and so forth, have led to impressive results in a myriad of applications, such as image and text generation (Radford et al., 2015; Hu et al., 2017; van den Oord et al., 2016), disentangled representation learning (Chen et al., 2016; Kulkarni et al., 2015), and semi-supervised learning (Salimans et al., 2016; Kingma et al., 2014). The deep generative model literature has largely viewed these approaches as distinct model training paradigms. For instance, GANs aim to achieve an equilibrium between a generator and a discrimi- nator; while VAEs are devoted to maximizing a variational lower bound of the data log-likelihood. A rich array of theoretical analyses and model extensions have been developed independently for GANs (Arjovsky & Bottou, 2017; Arora et al., 2017; Salimans et al., 2016; Nowozin et al., 2016) and VAEs (Burda et al., 2015; Chen et al., 2017; Hu et al., 2017), respectively. A few works attempt to combine the two objectives in a single model for improved inference and sample gener- ation (Mescheder et al., 2017; Larsen et al., 2015; Makhzani et al., 2015; Sønderby et al., 2017). Despite the significant progress specific to each method, it remains unclear how these apparently divergent approaches connect to each other in a principled way. In this paper, we present a new formulation of GANs and VAEs that connects them under a unified view, and links them back to the classic wake-sleep algorithm. We show that GANs and VAEs involve minimizing opposite KL divergences of respective posterior and inference distributions, and extending the sleep and wake phases, respectively, for generative model learning. More specifically, we develop a reformulation of GANs that interprets generation of samples as performing posterior inference, leading to an objective that resembles variational inference as in VAEs. As a counterpart, VAEs in our interpretation contain a degenerated adversarial mechanism that blocks out generated samples and only allows real examples for model training. The proposed interpretation provides a useful tool to analyze the broad class of recent GAN- and VAE- based algorithms, enabling perhaps a more principled and unified view of the landscape of generative modeling. For instance, one can easily extend our formulation to subsume InfoGAN (Chen et al., 2016) that additionally infers hidden representations of examples, VAE/GAN joint models (Larsen et al., 2015; Che et al., 2017a) that offer improved generation and reduced mode missing, and adver- sarial domain adaptation (ADA) (Ganin et al., 2016; Purushotham et al., 2017) that is traditionally framed in the discriminative setting. The close parallelisms between GANs and VAEs further ease transferring techniques that were originally developed for improving each individual class of models, to in turn benefit the other class. We provide two examples in such spirit: 1) Drawn inspiration from importance weighted VAE (IWAE) (Burda et al., 2015), we straightforwardly derive importance weighted GAN (IWGAN) that maximizes a tighter lower bound on the marginal likelihood compared to the vanilla GAN. 2) Motivated by the GAN adversarial game we activate the originally degenerated discriminator in VAEs, resulting in a full-fledged model that adaptively leverages both real and fake examples for learning. Empirical results show that the techniques imported from the other class are generally applicable to the base model and its variants, yielding consistently better performance.\n\nSection Title: RELATED WORK\n RELATED WORK There has been a surge of research interest in deep generative models in recent years, with remarkable progress made in understanding several class of algorithms. The wake-sleep algorithm (Hinton et al., 1995) is one of the earliest general approaches for learning deep generative models. The algorithm incorporates a separate inference model for posterior approximation, and aims at maximizing a variational lower bound of the data log-likelihood, or equivalently, minimizing the KL divergence of the approximate posterior and true posterior. However, besides the wake phase that minimizes the KL divergence w.r.t the generative model, the sleep phase is introduced for tractability that minimizes instead the reversed KL divergence w.r.t the inference model. Recent approaches such as NVIL (Mnih & Gregor, 2014) and VAEs (Kingma & Welling, 2013) are developed to maximize the variational lower bound w.r.t both the generative and inference models jointly. To reduce the variance of stochastic gradient estimates, VAEs leverage reparametrized gradients. Many works have been done along the line of improving VAEs. Burda et al. (2015) develop importance weighted VAEs to obtain a tighter lower bound. As VAEs do not involve a sleep phase-like procedure, the model cannot leverage samples from the generative model for model training. Hu et al. (2017) combine VAEs with an extended sleep procedure that exploits generated samples for learning. Another emerging family of deep generative models is the Generative Adversarial Networks (GANs) (Goodfellow et al., 2014), in which a discriminator is trained to distinguish between real and generated samples and the generator to confuse the discriminator. The adversarial approach can be alternatively motivated in the perspectives of approximate Bayesian computation (Gutmann et al., 2014) and density ratio estimation (Mohamed & Lakshminarayanan, 2016). The original objective of the generator is to minimize the log probability of the discriminator correctly recognizing a generated sample as fake. This is equivalent to minimizing a lower bound on the Jensen-Shannon divergence (JSD) of the generator and data distributions (Goodfellow et al., 2014; Nowozin et al., 2016; Huszar, 2016; Li, 2016). Besides, the objective suffers from vanishing gradient with strong discriminator. Thus in practice people have used another objective which maximizes the log probability of the discriminator recognizing a generated sample as real (Goodfellow et al., 2014; Arjovsky & Bottou, 2017). The second objective has the same optimal solution as with the original one. We base our analysis of GANs on the second objective as it is widely used in practice yet few theoretic analysis has been done on it. Numerous extensions of GANs have been developed, including combination with VAEs for improved generation (Larsen et al., 2015; Makhzani et al., 2015; Che et al., 2017a), and generalization of the objectives to minimize other f-divergence criteria beyond JSD (Nowozin et al., 2016; Sønderby et al., 2017). The adversarial principle has gone beyond the generation setting and been applied to other contexts such as domain adaptation (Ganin et al., 2016; Purushotham et al., 2017), and Bayesian inference (Mescheder et al., 2017; Tran et al., 2017; Huszár, 2017; Rosca et al., 2017) which uses implicit variational distributions in VAEs and leverage the adversarial approach for optimization. This paper starts from the basic models of GANs and VAEs, and develops a general formulation that reveals underlying connections of different classes of approaches including many of the above variants, yielding a unified view of the broad set of deep generative modeling.\n\nSection Title: BRIDGING THE GAP\n BRIDGING THE GAP The structures of GANs and VAEs are at the first glance quite different from each other. VAEs are based on the variational inference approach, and include an explicit inference model that reverses the generative process defined by the generative model. On the contrary, in traditional view GANs lack an inference model, but instead have a discriminator that judges generated samples. In this paper, a key idea to bridge the gap is to interpret the generation of samples in GANs as performing inference, and the discrimination as a generative process that produces real/fake labels. The resulting new formulation reveals the connections of GANs to traditional variational inference. The reversed generation-inference interpretations between GANs and VAEs also expose their correspondence to the two learning phases in the classic wake-sleep algorithm. For ease of presentation and to establish a systematic notation for the paper, we start with a new interpretation of Adversarial Domain Adaptation (ADA) (Ganin et al., 2016), the application of adversarial approach in the domain adaptation context. We then show GANs are a special case of ADA, followed with a series of analysis linking GANs, VAEs, and their variants in our formulation.\n\nSection Title: ADVERSARIAL DOMAIN ADAPTATION (ADA)\n ADVERSARIAL DOMAIN ADAPTATION (ADA) ADA aims to transfer prediction knowledge learned from a source domain to a target domain, by learning domain-invariant features (Ganin et al., 2016). That is, it learns a feature extractor whose output cannot be distinguished by a discriminator between the source and target domains. We first review the conventional formulation of ADA. Figure 1(a) illustrates the computation flow. Let z be a data example either in the source or target domain, and y ∈ {0, 1} the domain indicator with y = 0 indicating the target domain and y = 1 the source domain. The data distributions conditioning on the domain are then denoted as p(z|y). The feature extractor G θ parameterized with θ maps z to feature x = G θ (z). To enforce domain invariance of feature x, a discriminator D φ is learned. Specifically, D φ (x) outputs the probability that x comes from the source domain, and the discriminator is trained to maximize the binary classification accuracy of recognizing the domains: The feature extractor G θ is then trained to fool the discriminator: Please see the supplementary materials for more details of ADA. With the background of conventional formulation, we now frame our new interpretation of ADA. The data distribution p(z|y) and deterministic transformation G θ together form an implicit distribution over x, denoted as p θ (x|y), which is intractable to evaluate likelihood but easy to sample from. Let p(y) be the distribution of the domain indicator y, e.g., a uniform distribution as in Eqs.(1)-(2). The discriminator defines a conditional distribution q φ (y|x) = D φ (x). Let q r φ (y|x) = q φ (1 − y|x) be the reversed distribution over domains. The objectives of ADA are therefore rewritten as (omitting the constant scale factor 2): Note that z is encapsulated in the implicit distribution p θ (x|y). The only difference of the objectives of θ from φ is the replacement of q(y|x) with q r (y|x). This is where the adversarial mechanism comes about. We defer deeper interpretation of the new objectives in the next subsection.\n\nSection Title: GENERATIVE ADVERSARIAL NETWORKS (GANS)\n GENERATIVE ADVERSARIAL NETWORKS (GANS) GANs (Goodfellow et al., 2014) can be seen as a special case of ADA. Taking image generation for example, intuitively, we want to transfer the properties of real image (source domain) to generated image (target domain), making them indistinguishable to the discriminator. Figure 1(b) shows the conventional view of GANs. Formally, x now denotes a real example or a generated sample, z is the respective latent code. For the generated sample domain (y = 0), the implicit distribution p θ (x|y = 0) is defined by the prior of z and the generator G θ (z), which is also denoted as p g θ (x) in the literature. For the real example domain (y = 1), the code space and generator are degenerated, and we are directly presented with a fixed distribution p(x|y = 1), which is just the real data distribution p data (x). Note that p data (x) is also an implicit distribution and allows efficient empirical sampling. In summary, the conditional distribution over x is constructed as Here, free parameters θ are only associated with p g θ (x) of the generated sample domain, while p data (x) is constant. As in ADA, discriminator D φ is simultaneously trained to infer the probability that x comes from the real data domain. That is, q φ (y = 1|x) = D φ (x). With the established correspondence between GANs and ADA, we can see that the objectives of GANs are precisely expressed as Eq.(3). To make this clearer, we recover the classical form by unfolding over y and plugging in conventional notations. For instance, the objective of the generative parameters θ in Eq.(3) is translated into where p(y) is uniform and results in the constant scale factor 1/2. As noted in sec.2, we focus on the unsaturated objective for the generator (Goodfellow et al., 2014), as it is commonly used in practice yet still lacks systematic analysis.\n\nSection Title: New Interpretation\n New Interpretation Let us take a closer look into the form of Eq.(3). It closely resembles the data reconstruction term of a variational lower bound by treating y as visible variable while x as latent (as in ADA). That is, we are essentially reconstructing the real/fake indicator y (or its reverse 1 − y) with the \"generative distribution\" q φ (y|x) and conditioning on x from the \"inference distribution\" p θ (x|y). Figure 1(c) shows a schematic graphical model that illustrates such generative and inference processes. (Sec.D in the supplementary materials gives an example of translating a given schematic graphical model into mathematical formula.) We go a step further to reformulate the objectives and reveal more insights to the problem. In particular, for each optimization step of p θ (x|y) at point (θ 0 , φ 0 ) in the parameter space, we have: \" # = 1 = ()*) ( ) \" # = 0 = . / # ( ) 1 ( | = 0) \" 345 = 0 = . / 345 ( ) missed mode where KL(· ·) and JSD(· ·) are the KL and Jensen-Shannon Divergences, respectively. Proofs are in the supplements (sec.B). Eq.(6) offers several insights into the GAN generator learning: • Resemblance to variational inference. As above, we see x as latent and p θ (x|y) as the inference distribution. The p θ0 (x) is fixed to the starting state of the current update step, and can naturally be seen as the prior over x. By definition q r (x|y) that combines the prior p θ0 (x) and the generative distribution q r φ0 (y|x) thus serves as the posterior. Therefore, optimizing the generator G θ is equivalent to minimizing the KL divergence between the inference distribution and the posterior (a standard from of variational inference), minus a JSD between the distributions p g θ (x) and p data (x). The interpretation further reveals the connections to VAEs, as discussed later. • Training dynamics. By definition, p θ0 (x) = (p g θ 0 (x)+p data (x))/2 is a mixture of p g θ 0 (x) and p data (x) with uniform mixing weights, so the posterior q r (x|y) ∝ q r φ0 (y|x)p θ0 (x) is also a mix- ture of p g θ 0 (x) and p data (x) with mixing weights induced from the discriminator q r φ0 (y|x). For the KL divergence to minimize, the component with y = 1 is KL (p θ (x|y = 1) q r (x|y = 1)) = KL (p data (x) q r (x|y = 1)) which is a constant. The active component for optimization is with y = 0, i.e., KL (p θ (x|y = 0) q r (x|y = 0)) = KL (p g θ (x) q r (x|y = 0)). Thus, minimizing the KL divergence in effect drives p g θ (x) to a mixture of p g θ 0 (x) and p data (x). Since p data (x) is fixed, p g θ (x) gets closer to p data (x). Figure 2 illustrates the training dynamics schematically. • The JSD term. The negative JSD term is due to the introduction of the prior p θ0 (x). This term pushes p g θ (x) away from p data (x), which acts oppositely from the KLD term. However, we show that the JSD term is upper bounded by the KLD term (sec.C). Thus, if the KLD term is sufficiently minimized, the magnitude of the JSD also decreases. Note that we do not mean the JSD is insignificant or negligible. Instead conclusions drawn from Eq.(6) should take the JSD term into account. • Explanation of missing mode issue. JSD is a symmetric divergence measure while KLD is non-symmetric. The missing mode behavior widely observed in GANs (Metz et al., 2017; Che et al., 2017a) is thus explained by the asymmetry of the KLD which tends to concentrate p θ (x|y) to large modes of q r (x|y) and ignore smaller ones. See Figure 2 for the illustration. Concentration to few large modes also facilitates GANs to generate sharp and realistic samples. • Optimality assumption of the discriminator. Previous theoretical works have typically assumed (near) optimal discriminator (Goodfellow et al., 2014; Arjovsky & Bottou, 2017): q φ 0 (y|x) ≈ p θ 0 (x|y = 1) p θ 0 (x|y = 0) + p θ 0 (x|y = 1) = p data (x) pg θ 0 (x) + p data (x) , (7) which can be unwarranted in practice due to limited expressiveness of the discriminator (Arora et al., 2017). In contrast, our result does not rely on the optimality assumptions. Indeed, our result is a generalization of the previous theorem in (Arjovsky & Bottou, 2017), which is recovered by plugging Eq.(7) into Eq.(6): ∇ θ − E p θ (x|y)p(y) log q r φ 0 (y|x) θ=θ 0 = ∇ θ 1 2 KL (pg θ p data ) − JSD (pg θ p data ) θ=θ 0 , (8) which gives simplified explanations of the training dynamics and the missing mode issue only when the discriminator meets certain optimality criteria. Our generalized result enables understanding of broader situations. For instance, when the discriminator distribution q φ0 (y|x) gives uniform guesses, or when p g θ = p data that is indistinguishable by the discriminator, the gradients of the KL and JSD terms in Eq.(6) cancel out, which stops the generator learning. InfoGAN Chen et al. (2016) developed InfoGAN which additionally recovers (part of) the latent code z given sample x. This can straightforwardly be formulated in our framework by introducing an extra conditional q η (z|x, y) parameterized by η. As discussed above, GANs assume a degenerated code space for real examples, thus q η (z|x, y = 1) is fixed without free parameters to learn, and η is only associated to y = 0. The InfoGAN is then recovered by combining q η (z|x, y) with q φ (y|x) in Eq.(3) to perform full reconstruction of both z and y: Again, note that z is encapsulated in the implicit distribution p θ (x|y). The model is expressed as the schematic graphical model in Figure 1(d). Let q r (x|z, y) ∝ q η0 (z|x, y)q r φ0 (y|x)p θ0 (x) be the augmented \"posterior\", the result in the form of Lemma.1 still holds by adding z-related conditionals: The new formulation is also generally applicable to other GAN-related variants, such as Adversar- ial Autoencoder (Makhzani et al., 2015), Predictability Minimization (Schmidhuber, 1992), and cycleGAN (Zhu et al., 2017). In the supplements we provide interpretations of the above models.\n\nSection Title: VARIATIONAL AUTOENCODERS (VAES)\n VARIATIONAL AUTOENCODERS (VAES) We next explore the second family of deep generative modeling. The resemblance of GAN generator learning to variational inference (Lemma.1) suggests strong relations between VAEs (Kingma & Welling, 2013) and GANs. We build correspondence between them, and show that VAEs involve minimizing a KLD in an opposite direction, with a degenerated adversarial discriminator. The conventional definition of VAEs is written as: max θ,η L vae θ,η = E p data (x) Eq η (z|x) [logp θ (x|z)] − KL(qη(z|x) p(z)) , (11) wherep θ (x|z) is the generator,q η (z|x) the inference model, andp(z) the prior. The parameters to learn are intentionally denoted with the notations of corresponding modules in GANs. VAEs appear to differ from GANs greatly as they use only real examples and lack adversarial mechanism. To connect to GANs, we assume a perfect discriminator q * (y|x) which always predicts y = 1 with probability 1 given real examples, and y = 0 given generated samples. Again, for notational simplicity, let q r * (y|x) = q * (1 − y|x) be the reversed distribution. Lemma 2. Let p θ (z, y|x) ∝ p θ (x|z, y)p(z|y)p(y). The VAE objective L vae θ,η in Eq.(11) is equivalent to (omitting the constant scale factor 2): Here most of the components have exact correspondences (and the same definitions) in GANs and InfoGAN (see Table 1 ), except that the generation distribution p θ (x|z, y) differs slightly from its Components ADA GANs / InfoGAN VAEs x features data/generations data/generations y domain indicator real/fake indicator real/fake indicator (degenerated) z data examples code vector code vector p θ (x|y) feature distr. [I] generator, Eq.4 [G] p θ (x|z, y), generator, Eq.13 q φ (y|x) discriminator [G] discriminator [I] q*(y|x), discriminator (degenerated) qη(z|x, y) - [G] infer net (InfoGAN) [I] infer net KLD to min same as GANs counterpart p θ (x|y) in Eq.(4) to additionally account for the uncertainty of generating x given z: We provide the proof of Lemma 2 in the supplementary materials. Figure 1(e) shows the schematic graphical model of the new interpretation of VAEs, where the only difference from InfoGAN (Figure 1(d)) is swapping the solid-line arrows (generative process) and dashed-line arrows (inference). As in GANs and InfoGAN, for the real example domain with y = 1, both q η (z|x, y = 1) and p θ (x|z, y = 1) are constant distributions. Since given a fake sample x from p θ0 (x), the reversed perfect discriminator q r * (y|x) always predicts y = 1 with probability 1, the loss on fake samples is therefore degenerated to a constant, which blocks out fake samples from contributing to learning.\n\nSection Title: CONNECTING GANS AND VAES\n CONNECTING GANS AND VAES Table 1 summarizes the correspondence between the approaches. Lemma.1 and Lemma.2 have revealed that both GANs and VAEs involve minimizing a KLD of respective inference and posterior distributions. In particular, GANs involve minimizing the KL p θ (x|y) q r (x|y) while VAEs the KL q η (z|x, y)q r * (y|x) p θ (z, y|x) . This exposes several new connections between the two model classes, each of which in turn leads to a set of existing research, or can inspire new research directions: 1) As discussed in Lemma.1, GANs now also relate to the variational inference algorithm as with VAEs, revealing a unified statistical view of the two classes. Moreover, the new perspective naturally enables many of the extensions of VAEs and vanilla variational inference algorithm to be transferred to GANs. We show an example in the next section. 2) The generator parameters θ are placed in the opposite directions in the two KLDs. The asymmetry of KLD leads to distinct model behaviors. For instance, as discussed in Lemma.1, GANs are able to generate sharp images but tend to collapse to one or few modes of the data (i.e., mode missing). In contrast, the KLD of VAEs tends to drive generator to cover all modes of the data distribution but also small-density regions (i.e., mode covering), which usually results in blurred, implausible samples. This naturally inspires combination of the two KLD objectives to remedy the asymmetry. Previous works have explored such combinations, though motivated in different perspectives (Larsen et al., 2015; Che et al., 2017a; Pu et al., 2017). We discuss more details in the supplements. 3) VAEs within our formulation also include an adversarial mechanism as in GANs. The discriminator is perfect and degenerated, disabling generated samples to help with learning. This inspires activating the adversary to allow learning from samples. We present a simple possible way in the next section. 4) GANs and VAEs have inverted latent-visible treatments of (z, y) and x, since we interpret sample generation in GANs as posterior inference. Such inverted treatments strongly relates to the symmetry of the sleep and wake phases in the wake-sleep algorithm, as presented shortly. In sec.6, we provide a more general discussion on a symmetric view of generation and inference.\n\nSection Title: CONNECTING TO WAKE SLEEP ALGORITHM (WS)\n CONNECTING TO WAKE SLEEP ALGORITHM (WS) Wake-sleep algorithm (Hinton et al., 1995) was proposed for learning deep generative models such as Helmholtz machines (Dayan et al., 1995). WS consists of wake phase and sleep phase, which optimize the generative model and inference model, respectively. We follow the above notations, and introduce new notations h to denote general latent variables and λ to denote general parameters. The wake sleep algorithm is thus written as: Briefly, the wake phase updates the generator parameters θ by fitting p θ (x|h) to the real data and hidden code inferred by the inference model q λ (h|x). On the other hand, the sleep phase updates the parameters λ based on the generated samples from the generator. The relations between WS and VAEs are clear in previous discussions (Bornschein & Bengio, 2014; Kingma & Welling, 2013). Indeed, WS was originally proposed to minimize the variational lower bound as in VAEs (Eq.11) with the sleep phase approximation (Hinton et al., 1995). Alternatively, VAEs can be seen as extending the wake phase. Specifically, if we let h be z and λ be η, the wake phase objective recovers VAEs (Eq.11) in terms of generator optimization (i.e., optimizing θ). Therefore, we can see VAEs as generalizing the wake phase by also optimizing the inference model q η , with additional prior regularization on code z. On the other hand, GANs closely resemble the sleep phase. To make this clearer, let h be y and λ be φ. This results in a sleep phase objective identical to that of optimizing the discriminator q φ in Eq.(3), which is to reconstruct y given sample x. We thus can view GANs as generalizing the sleep phase by also optimizing the generative model p θ to reconstruct reversed y. InfoGAN (Eq.9) further extends the correspondence to reconstruction of latents z.\n\nSection Title: TRANSFERRING TECHNIQUES\n TRANSFERRING TECHNIQUES The new interpretation not only reveals the connections underlying the broad set of existing ap- proaches, but also facilitates to exchange ideas and transfer techniques across the two classes of algorithms. For instance, existing enhancements on VAEs can straightforwardly be applied to improve GANs, and vice versa. This section gives two examples. Here we only outline the main intuitions and resulting models, while providing the details in the supplement materials. 4.1 IMPORTANCE WEIGHTED GANS (IWGAN) Burda et al. (2015) proposed importance weighted autoencoder (IWAE) that maximizes a tighter lower bound on the marginal likelihood. Within our framework it is straightforward to develop importance weighted GANs by copying the derivations of IWAE side by side, with little adaptations. Specifically, the variational inference interpretation in Lemma.1 suggests GANs can be viewed as maximizing a lower bound of the marginal likelihood on y (putting aside the negative JSD term): Following (Burda et al., 2015), we can derive a tighter lower bound through a k-sample importance weighting estimate of the marginal likelihood. With necessary approximations for tractability, optimizing the tighter lower bound results in the following update rule for the generator learning: As in GANs, only y = 0 (i.e., generated samples) is effective for learning parameters θ. Compared to the vanilla GAN update (Eq.(6)), the only difference here is the additional importance weight w i which is the normalization of w i = q r φ 0 (y|xi) q φ 0 (y|xi) over k samples. Intuitively, the algorithm assigns higher weights to samples that are more realistic and fool the discriminator better, which is consistent to IWAE that emphasizes more on code states providing better reconstructions. Hjelm et al. (2017); Che et al. (2017b) developed a similar sample weighting scheme for generator training, while their generator of discrete data depends on explicit conditional likelihood. In practice, the k samples correspond to sample minibatch in standard GAN update. Thus the only computational cost added by the importance weighting method is by evaluating the weight for each sample, and is negligible. The discriminator is trained in the same way as in standard GANs. In the semi-supervised VAE (SVAE) setting, remaining training data are used for unsupervised training.\n\nSection Title: ADVERSARY ACTIVATED VAES (AAVAE)\n ADVERSARY ACTIVATED VAES (AAVAE) By Lemma.2, VAEs include a degenerated discriminator which blocks out generated samples from contributing to model learning. We enable adaptive incorporation of fake samples by activating the adversarial mechanism. Specifically, we replace the perfect discriminator q * (y|x) in VAEs with a discriminator network q φ (y|x) parameterized with φ, resulting in an adapted objective of Eq.(12): As detailed in the supplementary material, the discriminator is trained in the same way as in GANs. The activated discriminator enables an effective data selection mechanism. First, AAVAE uses not only real examples, but also generated samples for training. Each sample is weighted by the inverted discriminator q r φ (y|x), so that only those samples that resemble real data and successfully fool the discriminator will be incorporated for training. This is consistent with the importance weighting strategy in IWGAN. Second, real examples are also weighted by q r φ (y|x). An example receiving large weight indicates it is easily recognized by the discriminator, which means the example is hard to be simulated from the generator. That is, AAVAE emphasizes more on harder examples.\n\nSection Title: EXPERIMENTS\n EXPERIMENTS We conduct preliminary experiments to demonstrate the generality and effectiveness of the importance weighting (IW) and adversarial activating (AA) techniques. In this paper we do not aim at achieving state-of-the-art performance, but leave it for future work. In particular, we show the IW and AA extensions improve the standard GANs and VAEs, as well as several of their variants, respectively. We present the results here, and provide details of experimental setups in the supplements.\n\nSection Title: IMPORTANCE WEIGHTED GANS\n IMPORTANCE WEIGHTED GANS We extend both vanilla GANs and class-conditional GANs (CGAN) with the IW method. The base GAN model is implemented with the DCGAN architecture and hyperparameter setting (Radford et al., 2015). Hyperparameters are not tuned for the IW extensions. We use MNIST, SVHN, and CIFAR10 for evaluation. For vanilla GANs and its IW extension, we measure inception scores (Salimans et al., 2016) on the generated samples. For CGANs we evaluate the accuracy of conditional generation (Hu et al., 2017) with a pre-trained classifier. Please see the supplements for more details. Table 2 , left panel, shows the inception scores of GANs and IW-GAN, and the middle panel gives the classification accuracy of CGAN and and its IW extension. We report the averaged results ± one standard deviation over 5 runs. The IW strategy gives consistent improvements over the base models.\n\nSection Title: ADVERSARY ACTIVATED VAES\n ADVERSARY ACTIVATED VAES We apply the AA method on vanilla VAEs, class-conditional VAEs (CVAE), and semi-supervised VAEs (SVAE) (Kingma et al., 2014), respectively. We evaluate on the MNIST data. We measure the variational lower bound on the test set, with varying number of real training examples. For each batch of real examples, AA extended models generate equal number of fake samples for training. Table 3 shows the results of activating the adversarial mechanism in VAEs. Generally, larger improvement is obtained with smaller set of real training data. Table 2 , right panel, shows the improved accuracy of AA-SVAE over the base semi-supervised VAE.\n\nSection Title: DISCUSSIONS: SYMMETRIC VIEW OF GENERATION AND INFERENCE\n DISCUSSIONS: SYMMETRIC VIEW OF GENERATION AND INFERENCE Our new interpretations of GANs and VAEs have revealed strong connections between them, and linked the emerging new approaches to the classic wake-sleep algorithm. The generality of the proposed formulation offers a unified statistical insight of the broad landscape of deep generative modeling, and encourages mutual exchange of techniques across research lines. One of the key ideas in our formulation is to interpret sample generation in GANs as performing posterior inference. This section provides a more general discussion of this point. Traditional modeling approaches usually distinguish between latent and visible variables clearly and treat them in very different ways. One of the key thoughts in our formulation is that it is not necessary to make clear boundary between the two types of variables (and between generation and inference), but instead, treating them as a symmetric pair helps with modeling and understanding. For instance, we treat the generation space x in GANs as latent, which immediately reveals the connection between GANs and adversarial domain adaptation, and provides a variational inference interpretation of the generation. A second example is the classic wake-sleep algorithm, where the wake phase reconstructs visibles conditioned on latents, while the sleep phase reconstructs latents conditioned on visibles (i.e., generated samples). Hence, visible and latent variables are treated in a completely symmetric manner. • Empirical data distributions are usually implicit, i.e., easy to sample from but intractable for evaluating likelihood. In contrast, priors are usually defined as explicit distributions, amiable for likelihood evaluation. • The complexity of the two distributions are different. Visible space is usually complex while latent space tends (or is designed) to be simpler. However, the adversarial approach in GANs and other techniques such as density ratio estimation (Mo- hamed & Lakshminarayanan, 2016) and approximate Bayesian computation (Beaumont et al., 2002) have provided useful tools to bridge the gap in the first point. For instance, implicit generative models such as GANs require only simulation of the generative process without explicit likelihood evaluation, hence the prior distributions over latent variables are used in the same way as the empirical data distributions, namely, generating samples from the distributions. For explicit likelihood-based models, adversarial autoencoder (AAE) leverages the adversarial approach to allow implicit prior distributions over latent space. Besides, a few most recent work (Mescheder et al., 2017; Tran et al., 2017; Huszár, 2017; Rosca et al., 2017) extends VAEs by using implicit variational distributions as the inference model. Indeed, the reparameterization trick in VAEs already resembles construction of implicit variational distributions (as also seen in the derivations of IWGANs in Eq.37). In these algorithms, adversarial approach is used to replace intractable minimization of the KL divergence between implicit variational distributions and priors. The second difference in terms of space complexity guides us to choose appropriate tools (e.g., adver- sarial approach v.s. reconstruction optimization, etc) to minimize the distance between distributions to learn and their targets. However, the tools chosen do not affect the underlying modeling mechanism.\n", "output": "[Significance and novelty]\n<Unifying deep generative models> The paper presents a novel framework that interprets GAN algorithms as performing a form of variational inference on a generative model, providing a new perspective on the relationship between GANs and VAEs.\n<Connections to other variational methods> The paper establishes connections between GANs and other variational methods such as f-GAN, providing insights into the relationship between different generative models.\n\n[Potential reasons for acceptance]\n<Thought-provoking perspective on GANs and VAEs> The paper's framework places GANs and VAEs within the same graphical model perspective, offering valuable insights and potentially shaping how these models are understood and utilized in the future.\n<Correct theory and supported claims> The paper's theoretical foundations are sound, and the experiments conducted support the claims made in the paper, contributing to its potential acceptance.\n\n[Potential reasons for rejection]\n<Dense and hard to follow at times> Some reviewers found the paper dense and difficult to follow, suggesting potential issues with accessibility and clarity that may impact its acceptance.\n<Lack of connection to alternate perspectives> The paper may be perceived as isolating itself by not explicitly discussing connections to alternate perspectives or prior related work, potentially affecting its acceptance.\n\n[Suggestions for improvement]\n<Clarity and accessibility> Consider restructuring the paper to improve clarity and accessibility, potentially by moving some content to the appendix and concentrating more on key results and key experiments.\n<Further discussion of related work> Provide more detailed discussion and connections to related work, such as f-GAN, to contextualize the paper within existing research and address potential isolation from prior observations.\n<Exploration of alternate datasets> Expand the experiments to include harder datasets such as CelebA, LSUN, and ImageNet to further validate the proposed framework and its applications.\n\n"} {"input": "[TITLE]\nOn the Information Bottleneck Theory of Deep Learning\n\n[ABSTRACT]\nThe practical successes of deep neural networks have not been matched by theoretical progress that satisfyingly explains their behavior. In this work, we study the information bottleneck (IB) theory of deep learning, which makes three specific claims: first, that deep networks undergo two distinct phases consisting of an initial fitting phase and a subsequent compression phase; second, that the compression phase is causally related to the excellent generalization performance of deep networks; and third, that the compression phase occurs due to the diffusion-like behavior of stochastic gradient descent. Here we show that none of these claims hold true in the general case. Through a combination of analytical results and simulation, we demonstrate that the information plane trajectory is predominantly a function of the neural nonlinearity employed: double-sided saturating nonlinearities like tanh yield a compression phase as neural activations enter the saturation regime, but linear activation functions and single-sided saturating nonlinearities like the widely used ReLU in fact do not. Moreover, we find that there is no evident causal connection between compression and generalization: networks that do not compress are still capable of generalization, and vice versa. Next, we show that the compression phase, when it exists, does not arise from stochasticity in training by demonstrating that we can replicate the IB findings using full batch gradient descent rather than stochastic gradient descent. Finally, we show that when an input domain consists of a subset of task-relevant and task-irrelevant information, hidden representations do compress the task-irrelevant information, although the overall information about the input may monotonically increase with training time, and that this compression happens concurrently with the fitting process rather than during a subsequent compression period.\n\n[CAPTIONS]\nFigure 1: Information plane dynamics and neural nonlinearities. (A) Replication of Shwartz-Ziv & Tishby (2017) for a network with tanh nonlinearities (except for the final classification layer which contains two sigmoidal neurons). The x-axis plots information between each layer and the input, while the y-axis plots information between each layer and the output. The color scale indicates training time in epochs. Each of the six layers produces a curve in the information plane with the input layer at far right, output layer at the far left. Different layers at the same epoch are connected by fine lines. (B) Information plane dynamics with ReLU nonlinearities (except for the final layer of 2 sigmoidal neurons). Here no compression phase is visible in the ReLU layers. For learning curves of both networks, see Appendix A. (C) Information plane dynamics for a tanh network of size 784 − 1024 − 20 − 20 − 20 − 10 trained on MNIST, estimated using the non-parametric kernel density mutual information estimator of Kolchinsky & Tracey (2017); Kolchinsky et al. (2017), no compression is observed except in the final classification layer with sigmoidal neurons. See Appendix B for the KDE MI method applied to the original Tishby dataset; additional results using a second popular nonparametric k-NN-based method (Kraskov et al., 2004); and results for other neural nonlinearities.\nFigure 2: Nonlinear compression in a minimal model. (A) A three neuron nonlinear network which receives Gaussian inputs x, multiplies by weight w 1 , and maps through neural nonlinearity f (·) to produce hidden unit activity h. (B) The continuous activity h is binned into a discrete variable T for the purpose of calculating mutual information. Blue: continuous tanh nonlinear activation function. Grey: Bin borders for 30 bins evenly spaced between -1 and 1. Because of the saturation in the sigmoid, a wide range of large magnitude net input values map to the same bin. (C) Mutual information with the input as a function of weight size w 1 for a tanh nonlinearity. Information increases for small w 1 and then decreases for large w 1 as all inputs land in one of the two bins corresponding to the saturation regions. (D) Mutual information with the input for the ReLU nonlinearity increases without bound. Half of all inputs land in the bin corresponding to zero activity, while the other half have information that scales with the size of the weights.\nFigure 3: Generalization and information plane dynamics in deep linear networks. (A) A linear teacher network generates a dataset by passing Gaussian inputs X through its weights and adding noise. (B) A deep linear student network is trained on the dataset (here the network has 1 hidden layer to allow comparison with Fig. 4A, see Supplementary Figure 18 for a deeper network). (C) Training and testing error over time. (D) Information plane dynamics. No compression is observed.\nFigure 4: Overtraining and information plane dynamics. (A) Average training and test mean square error for a deep linear network trained with SGD. Overtraining is substantial. Other parameters: N i = 100, P = 100, Number of hidden units = 100, Batch size = 5 (B) Information plane dynamics. No compression is observed, and information about the labels is lost during overtraining. (C) Average train and test accuracy (% correct) for nonlinear tanh networks exhibiting modest overfitting (N = 8). (D) Information plane dynamics. Overfitting occurs despite continued compression.\nFigure 5: Stochastic training and the information plane. (A) tanh network trained with SGD. (B) tanh network trained with BGD. (C) ReLU network trained with SGD. (D) ReLU network trained with BGD. Both random and non-random training procedures show similar information plane dynamics.\nFigure 6: Simultaneous fitting and compression. (A) For a task with a large task-irrelevant subspace in the input, a linear network shows no overall compression of information about the input. (B) The information with the task-relevant subspace increases robustly over training. (C) However, the information specifically about the task-irrelevant subspace does compress after initially growing as the network is trained.\n\n[CONTENT]\nSection Title: INTRODUCTION\n INTRODUCTION Deep neural networks ( Schmidhuber, 2015 ; LeCun et al., 2015 ) are the tool of choice for real-world tasks ranging from visual object recognition ( Krizhevsky et al., 2012 ), to unsupervised learning ( Goodfellow et al., 2014 ; Lotter et al., 2016 ) and reinforcement learning ( Silver et al., 2016 ). These practical successes have spawned many attempts to explain the performance of deep learning systems ( Kadmon & Sompolinsky, 2016 ), mostly in terms of the properties and dynamics of the optimization problem in the space of weights ( Saxe et al., 2014 ; Choromanska et al., 2015 ; Advani & Saxe, 2017 ), or the classes of functions that can be efficiently represented by deep networks ( Montufar et al., 2014 ; Poggio et al., 2017 ). This paper analyzes a recent inventive proposal to study the dynamics of learning through the lens of information theory ( Tishby & Zaslavsky, 2015 ; Shwartz-Ziv & Tishby, 2017 ). In this view, deep learning is a question of representation learning: each layer of a deep neural network can be seen as a set of summary statistics which contain some but not all of the information present in the input, while retaining as much information about the target output as possible. The amount of information in a hidden layer regarding the input and output can then be measured over the course of learning, yielding a picture of the optimization process in the information plane. Crucially, this method holds the promise to serve as a general analysis that can be used to compare different architectures, using the common currency of mutual information. Moreover, the elegant information bottleneck (IB) theory provides a fundamental bound on the amount of input compression and target output information that any representation can achieve ( Tishby et al., 1999 ). The IB bound thus serves as a method-agnostic ideal to which different architectures and algorithms may be compared. A preliminary empirical exploration of these ideas in deep neural networks has yielded striking findings ( Shwartz-Ziv & Tishby, 2017 ). Most saliently, trajectories in the information plane appear to consist of two distinct phases: an initial \"fitting\" phase where mutual information between the hidden layers and both the input and output increases, and a subsequent \"compression\" phase where mutual information between the hidden layers and the input decreases. It has been hypothesized that this compression phase is responsible for the excellent generalization performance of deep networks, and further, that this compression phase occurs due to the random diffusion-like behavior of stochastic gradient descent. Here we study these phenomena using a combination of analytical methods and simulation. In Section 2, we show that the compression observed by Shwartz-Ziv & Tishby (2017) arises primarily due to the double-saturating tanh activation function used. Using simple models, we elucidate the effect of neural nonlinearity on the compression phase. Importantly, we demonstrate that the ReLU activation function, often the nonlinearity of choice in practice, does not exhibit a compression phase. We discuss how this compression via nonlinearity is related to the assumption of binning or noise in the hidden layer representation. To better understand the dynamics of learning in the information plane, in Section 3 we study deep linear networks in a tractable setting where the mutual information can be calculated exactly. We find that deep linear networks do not compress over the course of training for the setting we examine. Further, we show a dissociation between generalization and compression. In Section 4, we investigate whether stochasticity in the training process causes compression in the information plane. We train networks with full batch gradient descent, and compare the results to those obtained with stochastic gradient descent. We find comparable compression in both cases, indicating that the stochasticity of SGD is not a primary factor in the observed compression phase. Moreover, we show that the two phases of SGD occur even in networks that do not compress, demonstrating that the phases are not causally related to compression. These results may seem difficult to reconcile with the intuition that compression can be necessary to attain good performance: if some input channels primarily convey noise, good generalization requires excluding them. Therefore, in Section 5 we study a situation with explicitly task-relevant and task-irrelevant input dimensions. We show that the hidden-layer mutual information with the task-irrelevant subspace does indeed drop during training, though the overall information with the input increases. However, instead of a secondary compression phase, this task-irrelevant information is compressed at the same time that the task- relevant information is boosted. Our results highlight the importance of noise assumptions in applying information theoretic analyses to deep learning systems, and put in doubt the generality of the IB theory of deep learning as an explanation of generalization performance in deep architectures.\n\nSection Title: COMPRESSION AND NEURAL NONLINEARITIES\n COMPRESSION AND NEURAL NONLINEARITIES The starting point for our analysis is the observation that changing the activation function can markedly change the trajectory of a network in the information plane. In Figure 1A, we show our replication of the result reported by Shwartz-Ziv & Tishby (2017) for networks with the tanh nonlinearity. 1 This replication was performed with the code supplied by the authors of Shwartz-Ziv & Tishby (2017) , and closely follows the experimental setup described therein. Briefly, a neural network with 7 fully connected hidden layers of width 12-10-7-5-4-3-2 is trained with stochastic gradient descent to produce a binary classification from a 12-dimensional input. In our replication we used 256 randomly selected samples per batch. The mutual information of the network layers with respect to the input and output variables is calculated by binning the neuron's tanh output activations into 30 equal intervals between -1 and 1. Discretized values for each neuron in each layer are then used to directly calculate the joint distributions, over the 4096 equally likely input patterns and true output labels. In line with prior work ( Shwartz-Ziv & Tishby, 2017 ), the dynamics in Fig. 1 show a transition between an initial fitting phase, during which information about the input increases, and a subsequent compression phase, during which information about the input decreases. We then modified the code to train deep networks using rectified linear activation functions (f (x) = max(0, x)). While the activities of tanh networks are bounded in the range [−1, 1], ReLU networks have potentially unbounded positive activities. To calculate mutual information, we first trained the ReLU networks, next identified their largest activity value over the course of training, and finally chose 100 evenly spaced bins between the minimum and maximum activity values to discretize the hidden layer activity. The resulting information plane dynamics are shown in Fig. 1B. The mutual information with the input monotonically increases in all ReLU layers, with no apparent compression phase. To see whether our results were an artifact of the small network size, toy dataset, or simple binning-based mutual information estimator we employed, we also trained larger networks on the MNIST dataset and computed mutual information using a state-of-the-art nonparametric kernel density estimator which assumes hidden activity is distributed as a mixture of Gaussians (see Appendix B for details). Fig. C-D show that, again, tanh networks compressed but ReLU networks did not. Appendix B shows that similar results also obtain with the popular nonparametric k-nearest-neighbor estimator of Kraskov et al. (2004) , and for other neural nonlinearities. Thus, the choice of nonlinearity substantively affects the dynamics in the information plane. To understand the impact of neural nonlinearity on the mutual information dynamics, we develop a minimal model that exhibits this phenomenon. In particular, consider the simple three neuron network shown in Fig. 2A. We assume a scalar Gaussian input distribution X ∼ N (0, 1), which is fed through the scalar first layer weight w 1 , and passed through a neural nonlinearity f (·), yielding the hidden unit activity h = f (w 1 X). To calculate the mutual information with the input, this hidden unit activity is then binned yielding the new discrete variable T = bin(h) (for instance, into 30 evenly spaced bins from -1 to 1 for the tanh nonlinearity). This binning process is depicted in Fig. 2B. In this simple setting, the mutual information I(T ; X) between the binned hidden layer activity T and the input X can be calculated exactly. In particular, I(T ; X) = H(T ) − H(T |X) (1) = H(T ) (2) = − N i=1 p i log p i (3) where H(·) denotes entropy, and we have used the fact that H(T |X) = 0 since T is a deterministic function of X. Here the probabilities p i = P (h ≥ b i and h < b i+1 ) are simply the probability that an input X produces a hidden unit activity that lands in bin i, defined by lower and upper bin limits b i and b i+1 respectively. This probability can be calculated exactly for monotonic nonlinearities f (·) using the cumulative density of X, where f −1 (·) is the inverse function of f (·). As shown in Fig. 2C-D, as a function of the weight w 1 , mutual information with the input first increases and then decreases for the tanh nonlinearity, but always increases for the ReLU nonlinearity. Intuitively, for small weights w 1 ≈ 0, neural activities lie near zero on the approximately linear part of the tanh function. Therefore f (w 1 X) ≈ w 1 X, yielding a rescaled Gaussian with information that grows with the size of the weights. However for very large weights w 1 → ∞, the tanh hidden unit nearly always saturates, yielding a discrete variable that concentrates in just two bins. This is more or less a coin flip, containing mutual information with the input of approximately 1 bit. Hence the distribution of T collapses to a much lower entropy distribution, yielding compression for large weight values. With the ReLU nonlinearity, half of the inputs are negative and land in the bin containing a hidden activity of zero. The other half are Gaussian distributed, and thus have entropy that increases with the size of the weight. Hence double-saturating nonlinearities can lead to compression of information about the input, as hidden units enter their saturation regime, due to the binning procedure used to calculate mutual information. The crux of the issue is that the actual I(h; X) is infinite, unless the network itself adds noise to the hidden layers. In particular, without added noise, the transformation from X to the continuous hidden activity h is deterministic and the mutual information I(h; X) would generally be -5 0 5 -1 -0.5 0 0.5 1 0 2 4 6 8 10 w 1 0 1 2 3 4 5 I(X;T) 0 2 4 6 8 10 w 1 0 0.5 1 1.5 2 2.5 I(X;T) ℎ (⋅) ( * Net input ( * ) Hidden activity ℎ Continuous activity Bin borders A B C D Tanh nonlinearity ReLU nonlinearity infinite (see Appendix C for extended discussion). Networks that include noise in their processing (e.g., Kolchinsky et al. (2017) ) can have finite I(T ; X). Otherwise, to obtain a finite MI, one must compute mutual information as though there were binning or added noise in the activations. But this binning/noise is not actually a part of the operation of the network, and is therefore somewhat arbitrary (different binning schemes can result in different mutual information with the input, as shown in Fig. 14 of Appendix C). We note that the binning procedure can be viewed as implicitly adding noise to the hidden layer activity: a range of X values map to a single bin, such that the mapping between X and T is no longer perfectly invertible ( Laughlin, 1981 ). The binning procedure is therefore crucial to obtaining a finite MI value, and corresponds approximately to a model where noise enters the system after the calculation of h, that is, T = h + , where is noise of fixed variance independent from h and X. This approach is common in information theoretic analyses of deterministic systems, and can serve as a measure of the complexity of a system's representation (see Sec 2.4 of Shwartz-Ziv & Tishby (2017) ). However, neither binning nor noise is present in the networks that Shwartz-Ziv & Tishby (2017) considered, nor the ones in Fig. 2 , either during training or testing. It therefore remains unclear whether robustness of a representation to this sort of noise in fact influences generalization performance in deep learning systems. Furthermore, the addition of noise means that different architectures may no longer be compared in a common currency of mutual information: the binning/noise structure is arbitrary, and architectures that implement an identical input-output map can nevertheless have different robustness to noise added in their internal representation. For instance, Appendix C describes a family of linear networks that compute exactly the same input-output map and therefore generalize identically, but yield different mutual information with respect to the input. Finally, we note that approaches which view the weights obtained from the training process as the random variables of interest may sidestep this issue ( Achille & Soatto, 2017 ). Hence when a tanh network is initialized with small weights and over the course of training comes to saturate its nonlinear units (as it must to compute most functions of practical interest, see discussion in Appendix D), it will enter a compression period where mutual information decreases. Figures 16-17 of Appendix E show histograms of neural activity over the course of training, demonstrating that activities in the tanh network enter the saturation regime during training. This nonlinearity-based compression furnishes another explanation for the observation that training slows down as tanh networks enter their compression phase ( Shwartz-Ziv & Tishby, 2017 ): some fraction of inputs have saturated the nonlinearities, reducing backpropagated error gradients.\n\nSection Title: INFORMATION PLANE DYNAMICS IN DEEP LINEAR NETWORKS\n INFORMATION PLANE DYNAMICS IN DEEP LINEAR NETWORKS The preceding section investigates the role of nonlinearity in the observed compression behavior, tracing the source to double-saturating nonlinearities and the binning methodology used to calculate mutual information. However, other mechanisms could lead to compression as well. Even without nonlinearity, neurons could converge to highly correlated activations, or project out irrelevant direc- tions of the input. These phenomena are not possible to observe in our simple three neuron minimal model, as they require multiple inputs and hidden layer activities. To search for these mechanisms, we turn to a tractable model system: deep linear neural networks ( Baldi & Hornik (1989) ; Fukumizu (1998) ; Saxe et al. (2014) ). In particular, we exploit recent results on the generalization dynamics in simple linear networks trained in a student-teacher setup ( Seung et al., 1992 ; Advani & Saxe, 2017 ). In a student-teacher setting, one \"student\" neural network learns to approximate the output of another \"teacher\" neural network. This setting is a way of generating a dataset with interesting structure that nevertheless allows exact calculation of the generalization performance of the network, exact calculation of the mutual information of the representation (without any binning procedure), and, though we do not do so here, direct comparison to the IB bound which is already known for linear Gaussian problems ( Chechik et al., 2005 ). We consider a scenario where a linear teacher neural network generates input and output examples which are then fed to a deep linear student network to learn (Fig. 3A). Following the formulation of ( Advani & Saxe, 2017 ), we assume multivariate Gaussian inputs X ∼ N (0, 1 Ni I Ni ) and a scalar output Y . The output is generated by the teacher network according to Y = W 0 X + o , where o ∼ N (0, σ 2 o ) represents aspects of the target function which cannot be represented by a neural network (that is, the approximation error or bias in statistical learning theory), and the teacher weights W o are drawn independently from N (0, σ 2 w ). Here, the weights of the teacher define the rule to be learned. The signal to noise ratio SNR = σ 2 w /σ 2 o determines the strength of the rule linking inputs to outputs relative to the inevitable approximation error. We emphasize that the \"noise\" added to the teacher's output is fundamentally different from the noise added for the purpose of calculating mutual information: o models the approximation error for the task-even the best possible neural network may still make errors because the target function is not representable exactly as a neural network-and is part of the construction of the dataset, not part of the analysis of the student network. To train the student network, a dataset of P examples is generated using the teacher. The student network is then trained to minimize the mean squared error between its output and the target output using standard (batch or stochastic) gradient descent on this dataset. Here the student is a deep linear neural network consisting of potentially many layers, but where the the activation function of each neuron is simply f (u) = u. That is, a depth D deep linear network computes the output Y = W D+1 W D · · · W 2 W 1 X. While linear activation functions stop the network from computing complex nonlinear functions of the input, deep linear networks nevertheless show complicated nonlinear learning trajectories ( Saxe et al., 2014 ), the optimization problem remains nonconvex ( Baldi & Hornik, 1989 ), and the generalization dynamics can exhibit substantial overtraining ( Fukumizu, 1998 ; Advani & Saxe, 2017 ). Importantly, because of the simplified setting considered here, the true generalization error is easily shown to be E g (t) = ||W o − W tot (t)|| 2 F +σ 2 o (5) where W tot (t) is the overall linear map implemented by the network at training epoch t (that is, W tot = W D+1 W D · · · W 2 W 1 ). Furthermore, the mutual information with the input and output may be calculated exactly, because the distribution of the activity of any hidden layer is Gaussian. Let T be the activity of a specific hidden layer, and letW be the linear map from the input to this activity (that is, for layer l,W = W l · · · W 2 W 1 ). Since T =W X, the mutual information of X and T calculated using differential entropy is infinite. For the purpose of calculating the mutual information, therefore, we assume that Gaussian noise is added to the hidden layer activity, T =W X + M I , with mean 0 and variance σ 2 M I = 1.0. This allows the analysis to apply to networks of any size, including overcomplete layers, but as before we emphasize that we do not add this noise either during training or testing. With these assumptions, T and X are jointly Gaussian and we have I(T ; X) = log|WW T + σ 2 M I I N h |− log|σ 2 M I I N h | (6) where |·| denotes the determinant of a matrix. Finally the mutual information with the output Y , also jointly Gaussian, can be calculated similarly (see Eqns. (22)-(25) of Appendix G). Fig. 3 shows example training and test dynamics over the course of learning in panel C, and the information plane dynamics in panel D. Here the network has an input layer of 100 units, 1 hidden layer of 100 units each and one output unit. The network was trained with batch gradient descent on a dataset of 100 examples drawn from the teacher with signal to noise ratio of 1.0. The linear network behaves qualitatively like the ReLU network, and does not exhibit compression. Nevertheless, it learns a map that generalizes well on this task and shows minimal overtraining. Hence, in the setting we study here, generalization performance can be acceptable without any compression phase. The results in ( Advani & Saxe (2017) ) show that, for the case of linear networks, overtraining is worst when the number of inputs matches the number of training samples, and is reduced by making the number of samples smaller or larger. Fig. 4 shows learning dynamics with the number of samples matched to the size of the network. Here overfitting is substantial, and again no compression is seen in the information plane. Comparing to the result in Fig. 3D, both networks exhibit similar information dynamics with respect to the input (no compression), but yield different generalization performance. Hence, in this linear analysis of a generic setting, there do not appear to be additional mechanisms that cause compression over the course of learning; and generalization behavior can be widely different for networks with the same dynamics of information compression regarding the input. We note that, in the setting considered here, all input dimensions have the same variance, and the weights of the teacher are drawn independently. Because of this, there are no special directions in the input, and each subspace of the input contains as much information as any other. It is possible that, in real world tasks, higher variance inputs are also the most likely to be relevant to the task (here, have large weights in the teacher). We have not investigated this possibility here. To see whether similar behavior arises in nonlinear networks, we trained tanh networks in the same setting as Section 2, but with 30% of the data, which we found to lead to modest overtraining. Fig. 4C-D shows the resulting train, test, and information plane dynamics. Here the tanh networks show substantial compression, despite exhibiting overtraining. This establishes a dissociation between behavior in the information plane and generalization dynamics: networks that compress may (Fig. 1A) or may not (Fig. 4C-D) generalize well, and networks that do not compress may (Figs.1B, 3A-B) or may not (Fig. 4A-B) generalize well.\n\nSection Title: COMPRESSION IN BATCH GRADIENT DESCENT AND SGD\n COMPRESSION IN BATCH GRADIENT DESCENT AND SGD Next, we test a core theoretical claim of the information bottleneck theory of deep learning, namely that randomness in stochastic gradient descent is responsible for the compression phase. In particular, because the choice of input samples in SGD is random, the weights evolve in a stochastic way during training. Shwartz-Ziv & Tishby (2017) distinguish two phases of SGD optimization: in the first \"drift\" phase, the mean of the gradients over training samples is large relative to the standard deviation of the gradients; in the second \"diffusion\" phase, the mean becomes smaller than the standard deviation of the gradients. The authors propose that compression should commence following the transition from a high to a low gradient signal-to-noise ratio (SNR), i.e., the onset of the diffusion phase. The proposed mechanism behind this diffusion-driven compression is as follows. The authors state that during the diffusion phase, the stochastic evolution of the weights can be described as a Fokker-Planck equation under the constraint of small training error. Then, the stationary distribution over weights for this process will have maximum entropy, again subject to the training error constraint. Finally, the authors claim that weights drawn from this stationary distribution will maximize the entropy of inputs given hidden layer activity, H(X|T ), subject to a training error constraint, and that this training error constraint is equivalent to a constraint on the mutual information I(T ; Y ) for small training error. Since the entropy of the input, H(X), is fixed, the result of the diffusion dynamics will be to minimize I(X; T ) := H(X) − H(X|T ) for a given value of I(T ; Y ) reached at the end of the drift phase. However, this explanation does not hold up to either theoretical or empirical investigation. Let us assume that the diffusion phase does drive the distribution of weights to a maximum entropy distribution subject to a training error constraint. Note that this distribution reflects stochasticity of weights across different training runs. There is no general reason that a given set of weights sampled from this distribution (i.e., the weight parameters found in one particular training run) will maximize H(X|T ), the entropy of inputs given hidden layer activity. In particular, H(X|T ) reflects (conditional) uncertainty about inputs drawn from the data-generating distribution, rather than uncertainty about any kind of distribution across different training runs. We also show empirically that the stochasticity of the SGD is not necessary for compression. To do so, we consider two distinct training procedures: offline stochastic gradient descent (SGD), which learns from a fixed-size dataset, and updates weights by repeatedly sampling a single example from the dataset and calculating the gradient of the error with respect to that single sample (the typical procedure used in practice); and batch gradient descent (BGD), which learns from a fixed-size dataset, and updates weights using the gradient of the total error across all examples. Batch gradient descent uses the full training dataset and, crucially, therefore has no randomness or diffusion-like behavior in its updates. We trained tanh and ReLU networks with SGD and BGD and compare their information plane dynamics in Fig. 5 (see Appendix H for a linear network). We find largely consistent information dynamics in both instances, with robust compression in tanh networks for both methods. Thus randomness in the training process does not appear to contribute substantially to compression of information about the input. This finding is consistent with the view presented in Section 2 that compression arises predominantly from the double saturating nonlinearity. Finally, we look at the gradient signal-to-noise ratio (SNR) to analyze the relationship between compression and the transition from high to low gradient SNR. Fig. 20 of Appendix I shows the gradient SNR over training, which in all cases shows a phase transition during learning. Hence the gradient SNR transition is a general phenomenon, but is not causally related to compression. Appendix I offers an extended discussion and shows gradient SNR transitions without compression on the MNIST dataset and for linear networks.\n\nSection Title: SIMULTANEOUS FITTING AND COMPRESSION\n SIMULTANEOUS FITTING AND COMPRESSION Our finding that generalization can occur without compression may seem difficult to reconcile with the intuition that certain tasks involve suppressing irrelevant directions of the input. In the extreme, if certain inputs contribute nothing but noise, then good generalization requires ignoring them. To study this, we consider a variant on the linear student-teacher setup of Section 3: we partition the input X into a set of task-relevant inputs X rel and a set of task-irrelevant inputs X irrel , and alter the teacher network so that the teacher's weights to the task-irrelevant inputs are all zero. Hence the inputs X irrel contribute only noise, while the X rel contain signal. We then calculate the information plane dynamics for the whole layer, and for the task-relevant and task-irrelevant inputs separately. Fig. 6 shows information plane dynamics for a deep linear neural network trained using SGD (5 samples/batch) on a task with 30 task-relevant inputs and 70 task-irrelevant inputs. While the overall dynamics show no compression phase, the information specifically about the task-irrelevant subspace does compress over the course of training. This compression process occurs at the same time as the fitting to the task-relevant information. Thus, when a task requires ignoring some inputs, the A B C information with these inputs specifically will indeed be reduced; but overall mutual information with the input in general may still increase.\n\nSection Title: DISCUSSION\n DISCUSSION Our results suggest that compression dynamics in the information plane are not a general feature of deep networks, but are critically influenced by the nonlinearities employed by the network. Double- saturating nonlinearities lead to compression, if mutual information is estimated by binning activations or by adding homoscedastic noise, while single-sided saturating nonlinearities like ReLUs do not compress in general. Consistent with this view, we find that stochasticity in the training process does not contribute to compression in the cases we investigate. Furthermore, we have found instances where generalization performance does not clearly track information plane behavior, questioning the causal link between compression and generalization. Hence information compression may parallel the situation with sharp minima: although empirical evidence has shown a correlation with generalization error in certain settings and architectures, further theoretical analysis has shown that sharp minima can in fact generalize well ( Dinh et al., 2017 ). We emphasize that compression still may occur within a subset of the input dimensions if the task demands it. This compression, however, is interleaved rather than in a secondary phase and may not be visible by information metrics that track the overall information between a hidden layer and the input. Finally, we note that our results address the specific claims of one scheme to link the information bottleneck principle with current practice in deep networks. The information bottleneck principle itself is more general and may yet offer important insights into deep networks ( Achille & Soatto, 2017 ). Moreover, the information bottleneck principle could yield fundamentally new training algorithms for networks that are inherently stochastic and where compression is explicitly encouraged with appropriate regularization terms ( Chalk et al., 2016 ; Alemi et al., 2017 ; Kolchinsky et al., 2017 ).\n", "output": "[Significance and novelty]\n<Challenging existing theory> The paper challenges the Information Bottleneck theory claims with consistent methodology, providing substantial arguments against it.\n<Thorough investigation> The paper contributes to the much-needed theory of deep learning rather than just focusing on another architecture, making it a significant contribution to the field.\n\n[Potential reasons for acceptance]\n<Well-executed experiments> The experiments are well-designed and executed, contributing to the significance of the paper.\n<Constructive part of ongoing discussion> The submission is seen as a constructive part of the ongoing discussion in the literature on furthering theoretical understanding of neural networks, making it a potential reason for acceptance.\n\n[Potential reasons for rejection]\n<Unclear theoretical exploration> The underlying theoretical causes for the limitations exposed empirically are not explored in depth, which may raise concerns about the paper's completeness.\n<Limitations of empirical evidence> The limitations exposed are based on empirical evidence, and the lack of exploration of underlying theoretical causes may be a reason for concern.\n\n[Suggestions for improvement]\n<More theoretical exploration> The paper could benefit from exploring the underlying theoretical causes for the limitations exposed empirically, providing a more comprehensive analysis.\n<Clarification on methodological choices> Justification for methodological choices such as binning in mutual information calculation and the influence of weight magnitude could be made clearer to enhance the paper's quality.\n<Additional figure styles and details> Adding figures that show the phase plane dynamics for other non-linearities and clarifying the use of batch gradient descent versus stochastic gradient descent could improve the completeness of the paper.\n<Figure improvement> The paper should address issues such as labels being hard to read and inconsistent figure styles to enhance readability and clarity.\n\n"}
{"messages": [{"role": "system", "content": "xxx"}, {"role": "user", "content": "xxx"}, {"role": "assistant", "content": "zzz"}]}
从而变成如下适应「gpt3.5 16k微调之用」的paper-review数据集
为了方便大家一目了然,我再把转换前后的样式贴出来 对比下{"messages": [{"role": "system", "content": "You are a professional machine learning conference reviewer who reviews a given paper and considers 4 criteria: ** importance and novelty **, ** potential reasons for acceptance **, ** potential reasons for rejection **, and ** suggestions for improvement **. \nThe given paper is as follows."}, {"role": "user", "content": "[TITLE]\nImage Quality Assessment Techniques Improve Training and Evaluation of Energy-Based Generative Adversarial Networks\n\n[ABSTRACT]\nWe propose a new, multi-component energy function for energy-based Generative Adversarial Networks (GANs) based on methods from the image quality assessment literature. Our approach expands on the Boundary Equilibrium Generative Adversarial Network (BEGAN) by outlining some of the short-comings of the original energy and loss functions. We address these short-comings by incorporating an l1 score, the Gradient Magnitude Similarity score, and a chrominance score into the new energy function. We then provide a set of systematic experiments that explore its hyper-parameters. We show that each of the energy function's components is able to represent a slightly different set of features, which require their own evaluation criteria to assess whether they have been adequately learned. We show that models using the new energy function are able to produce better image representations than the BEGAN model in predicted ways.\n\n[CAPTIONS]\nFigure 1: From left to right, the images are the original image, a contrast stretched image, an image with impulsive noise contamination, and a Gaussian smoothed image. Although these images differ greatly in quality, they all have the same MSE from the original image (about 400), suggesting that MSE is a limited technique for measuring image quality.\nFigure 2: Comparison of the gradient (edges in the image) for models 11 (BEGAN) and 12 (scaled BEGAN+GMSM), where O is the original image, A is the autoencoded image, OG is the gradient of the original image, AG is the gradient of the autoencoded image, and S is the gradient magnitude similarity score for the discriminator (D) and generator (G). White equals greater similarity (better performance) and black equals lower similarity for the final column.\nFigure 3: Comparison of the chrominance for models 9 (BEGAN+GMSM+Chrom), 11 (BEGAN) and 12 (scaled BEGAN+GMSM), where O is the original image, OC is the original image in the corresponding color space, A is the autoencoded image in the color space, and S is the chrominance similarity score. I and Q indicate the (blue-red) and (green-purple) color dimensions, respectively. All images were normalized relative to their maximum value to increase luminance. Note that pink and purple approximate a similarity of 1, and green and blue approximate a similarity of 0 for I and Q dimensions, respectively. The increased gradient 'speckling' of model 12Q suggests an inverse relationship between the GMSM and chrominance distance functions.\nTable 1: Models and their corresponding model distance function parameters. The l 1 , GMSM, and Chrom parameters are their respective β d values from Equation 8.\nTable 2: Lists the models, their discriminator mean error scores, and their standard deviations for the l 1 , GMSM, and chrominance distance functions over all training epochs. Bold values show the best scores for similar models. Double lines separate sets of similar models. Values that are both bold and italic indicate the best scores overall, excluding models that suffered from modal collapse. These results suggest that model training should be customized to emphasize the relevant components.\n\n[CONTENT]\nSection Title: INTRODUCTION\n INTRODUCTION\n\nSection Title: IMPROVING LEARNED REPRESENTATIONS FOR GENERATIVE MODELING\n IMPROVING LEARNED REPRESENTATIONS FOR GENERATIVE MODELING Radford et al. (2015) demonstrated that Generative Adversarial Networks (GANs) are a good unsu- pervised technique for learning representations of images for the generative modeling of 2D images. Since then, a number of improvements have been made. First, Zhao et al. (2016) modified the error signal of the deep neural network from the original, single parameter criterion to a multi-parameter criterion using auto-encoder reconstruction loss. Berthelot et al. (2017) then further modified the loss function from a hinge loss to the Wasserstein distance between loss distributions. For each modification, the proposed changes improved the resulting output to visual inspection (see Ap- pendix A Figure 4 , Row 1 for the output of the most recent, BEGAN model). We propose a new loss function, building on the changes of the BEGAN model (called the scaled BEGAN GMSM) that further modifies the loss function to handle a broader range of image features within its internal representation.\n\nSection Title: GENERATIVE ADVERSARIAL NETWORKS\n GENERATIVE ADVERSARIAL NETWORKS Generative Adversarial Networks are a form of two-sample or hypothesis testing that uses a classi- fier, called a discriminator, to distinguish between observed (training) data and data generated by the model or generator. Training is then simplified to a competing (i.e., adversarial) objective between the discriminator and generator, where the discriminator is trained to better differentiate training from generated data, and the generator is trained to better trick the discriminator into thinking its generated data is real. The convergence of a GAN is achieved when the generator and discriminator reach a Nash equilibrium, from a game theory point of view (Zhao et al., 2016). In the original GAN specification, the task is to learn the generator's distribution p G over data x ( Goodfellow et al., 2014 ). To accomplish this, one defines a generator function G(z; θ G ), which produces an image using a noise vector z as input, and G is a differentiable function with param- eters θ G . The discriminator is then specified as a second function D(x; θ D ) that outputs a scalar representing the probability that x came from the data rather than p G . D is then trained to maxi- mize the probability of assigning the correct labels to the data and the image output of G while G is trained to minimize the probability that D assigns its output to the fake class, or 1 − D(G(z)). Although G and D can be any differentiable functions, we will only consider deep convolutional neural networks in what follows. Zhao et al. (2016) initially proposed a shift from the original single-dimensional criterion-the scalar class probability-to a multidimensional criterion by constructing D as an autoencoder. The image output by the autoencoder can then be directly compared to the output of G using one of the many standard distance functions (e.g., l 1 norm, mean square error). However, Zhao et al. (2016) also proposed a new interpretation of the underlying GAN architecture in terms of an energy-based model ( LeCun et al., 2006 ).\n\nSection Title: ENERGY-BASED GENERATIVE ADVERSARIAL NETWORKS\n ENERGY-BASED GENERATIVE ADVERSARIAL NETWORKS The basic idea of energy-based models (EBMs) is to map an input space to a single scalar or set of scalars (called its \"energy\") via the construction of a function ( LeCun et al., 2006 ). Learning in this framework modifies the energy surface such that desirable pairings get low energies while undesir- able pairings get high energies. This framework allows for the interpretation of the discriminator (D) as an energy function that lacks any explicit probabilistic interpretation (Zhao et al., 2016). In this view, the discriminator is a trainable cost function for the generator that assigns low energy val- ues to regions of high data density and high energy to the opposite. The generator is then interpreted as a trainable parameterized function that produces samples in regions assigned low energy by the discriminator. To accomplish this setup, Zhao et al. (2016) first define the discriminator's energy function as the mean square error of the reconstruction loss of the autoencoder, or: Zhao et al. (2016) then define the loss function for their discriminator using a form of margin loss. L D (x, z) = E D (x) + [m − E D (G(z))] + (2) where m is a constant and [·] + = max(0, ·). They define the loss function for their generator: The authors then prove that, if the system reaches a Nash equilibrium, then the generator will pro- duce samples that cannot be distinguished from the dataset. Problematically, simple visual inspec- tion can easily distinguish the generated images from the dataset.\n\nSection Title: DEFINING THE PROBLEM\n DEFINING THE PROBLEM It is clear that, despite the mathematical proof of Zhao et al. (2016) , humans can distinguish the images generated by energy-based models from real images. There are two direct approaches that could provide insight into this problem, both of which are outlined in the original paper. The first approach that is discussed by Zhao et al. (2016) changes Equation 2 to allow for better approxima- tions than m. The BEGAN model takes this approach. The second approach addresses Equation 1, but was only implicitly addressed when (Zhao et al., 2016) chose to change the original GAN to use the reconstruction error of an autoencoder instead of a binary logistic energy function. We chose to take the latter approach while building on the work of BEGAN. Our main contributions are as follows: • An energy-based formulation of BEGAN's solution to the visual problem. • An energy-based formulation of the problems with Equation 1. • Experiments that explore the different hyper-parameters of the new energy function. • Evaluations that provide greater detail into the learned representations of the model. • A demonstration that scaled BEGAN+GMSM can be used to generate better quality images from the CelebA dataset at 128x128 pixel resolution than the original BEGAN model in quantifiable ways.\n\nSection Title: BOUNDARY EQUILIBRIUM GENERATIVE ADVERSARIAL NETWORKS\n BOUNDARY EQUILIBRIUM GENERATIVE ADVERSARIAL NETWORKS The Boundary Equilibrium Generative Adversarial Network (BEGAN) makes a number of modi- fications to the original energy-based approach. However, the most important contribution can be summarized in its changes to Equation 2. In place of the hinge loss, Berthelot et al. (2017) use the Wasserstein distance between the autoencoder reconstruction loss distributions of G and D. They also add three new hyper-parameters in place of m: k t , λ k , and γ. Using an energy-based approach, we get the following new equation: The value of k t is then defined as: k t+1 = k t + λ k (γE D (x) − E D (G(z))) for each t (5) where k t ∈ [0, 1] is the emphasis put on E(G(z)) at training step t for the gradient of E D , λ k is the learning rate for k, and γ ∈ [0, 1]. Both Equations 2 and 4 are describing the same phenomenon: the discriminator is doing well if either 1) it is properly reconstructing the real images or 2) it is detecting errors in the reconstruction of the generated images. Equation 4 just changes how the model achieves that goal. In the original equation (Equation 2), we punish the discriminator (L D → ∞) when the generated input is doing well (E D (G(z)) → 0). In Equation 4, we reward the discriminator (L D → 0) when the generated input is doing poorly (E D (G(z)) → ∞). What is also different between Equations 2 and 4 is the way their boundaries function. In Equation 2, m only acts as a one directional boundary that removes the impact of the generated input on the discriminator if E D (G(z)) > m. In Equation 5, γE D (x) functions in a similar but more complex way by adding a dependency to E D (x). Instead of 2 conditions on either side of the boundary m, there are now four: The optimal condition is condition 1 Berthelot et al. (2017) . Thus, the BEGAN model tries to keep the energy of the generated output approaching the limit of the energy of the real images. As the latter will change over the course of learning, the resulting boundary dynamically establishes an equilibrium between the energy state of the real and generated input. It is not particularly surprising that these modifications to Equation 2 show improvements. Zhao et al. (2016) devote an appendix section to the correct selection of m and explicitly mention that the \"balance between... real and fake samples[s]\" (italics theirs) is crucial to the correct selection of m. Unsurprisingly, a dynamically updated parameter that accounts for this balance is likely to be the best instantiation of the authors' intuitions and visual inspection of the resulting output supports this (see Berthelot et al., 2017 ). We chose a slightly different approach to improving the proposed loss function by changing the original energy function (Equation 1).\n\nSection Title: FINDING A NEW ENERGY FUNCTION VIA IMAGE QUALITY ASSESSMENT\n FINDING A NEW ENERGY FUNCTION VIA IMAGE QUALITY ASSESSMENT In the original description of the energy-based approach to GANs, the energy function was defined as the mean square error (MSE) of the reconstruction loss of the autoencoder (Equation 1). Our first insight was a trivial generalization of Equation 1: E(x) = δ(D(x), x) (6) where δ is some distance function. This more general equation suggests that there are many possible distance functions that could be used to describe the reconstruction error and that the selection of δ is itself a design decision for the resulting energy and loss functions. Not surprisingly, an entire field of study exists that focuses on the construction of similar δ functions in the image domain: the field of image quality assessment (IQA). The field of IQA focuses on evaluating the quality of digital images ( Wang & Bovik, 2006 ). IQA is a rich and diverse field that merits substantial further study. However, for the sake of this paper, we want to emphasize three important findings from this field. First, distance functions like δ are called full-reference IQA (or FR-IQA) functions because the reconstruction (D(x)) has a 'true' or undistorted reference image (x) which it can be evaluated from Wang et al. (2004) . Second, IQA researchers have known for a long time that MSE is a poor indicator of image quality ( Wang & Bovik, 2006 ). And third, there are numerous other functions that are better able to indicate image quality. We explain each of these points below. One way to view the FR-IQA approach is in terms of a reference and distortion vector. In this view, an image is represented as a vector whose dimensions correspond with the pixels of the image. The reference image sets up the initial vector from the origin, which defines the original, perfect image. The distorted image is then defined as another vector defined from the origin. The vector that maps the reference image to the distorted image is called the distortion vector and FR-IQA studies how to evaluate different types of distortion vectors. In terms of our energy-based approach and Equation 6, the distortion vector is measured by δ and it defines the surface of the energy function. MSE is one of the ways to measure distortion vectors. It is based in a paradigm that views the loss of quality in an image in terms of the visibility of an error signal, which MSE quantifies. Problem- atically, it has been shown that MSE actually only defines the length of a distortion vector not its type ( Wang & Bovik, 2006 ). For any given reference image vector, there are an entire hypersphere of other image vectors that can be reached by a distortion vector of a given size (i.e., that all have the same MSE from the reference image; see Figure 1 ). A number of different measurement techniques have been created that improve upon MSE (for a review, see Chandler, 2013 ). Often these techniques are defined in terms of the similarity (S) between the reference and distorted image, where δ = 1−S. One of the most notable improvements is the Structural Similarity Index (SSIM), which measures the similarity of the luminance, contrast, and structure of the reference and distorted image using the following similarity function: 2 S(v d , v r ) = 2v d v r + C v 2 d + v 2 r + C (7) where v d is the distorted image vector, v r is the reference image vector, C is a constant, and all multiplications occur element-wise Wang & Bovik (2006) . 3 This function has a number of desirable features. It is symmetric (i.e., S(v d , v r ) = S(v r , v d ), bounded by 1 (and 0 for x > 0), and it has a unique maximum of 1 only when v d = v r . Although we chose not to use SSIM as our energy function (δ) as it can only handle black-and-white images, its similarity function (Equation 7) informs our chosen technique. The above discussion provides some insights into why visual inspection fails to show this correspon- dence between real and generated output of the resulting models, even though Zhao et al. (2016) proved that the generator should produce samples that cannot be distinguished from the dataset. The original proof by Zhao et al. (2016) did not account for Equation 1. Thus, when Zhao et al. (2016) show that their generated output should be indistinguishable from real images, what they are actu- ally showing is that it should be indistinguishable from the real images plus some residual distortion vector described by δ. Yet, we have just shown that MSE (the author's chosen δ) can only constrain the length of the distortion vector, not its type. Consequently, it is entirely possible for two systems using MSE for δ to have both reached a Nash equilibrium, have the same energy distribution, and yet have radically different internal representations of the learned images. The energy function is as important as the loss function for defining the data distribution.\n\nSection Title: A NEW ENERGY FUNCTION\n A NEW ENERGY FUNCTION Rather than assume that any one distance function would suffice to represent all of the various features of real images, we chose to use a multi-component approach for defining δ. In place of the luminance, contrast, and structural similarity of SSIM, we chose to evaluate the l 1 norm, the gradient magnitude similarity score (GMS), and a chrominance similarity score (Chrom). We outline the latter two in more detail below. The GMS score and chrom scores derive from an FR-IQA model called the color Quality Score (cQS; Gupta et al., 2017 ). The cQS uses GMS and chrom as its two components. First, it converts images to the YIQ color space model. In this model, the three channels correspond to the luminance information (Y) and the chrominance information (I and Q). Second, GMS is used to evaluate the local gradients across the reference and distorted images on the luminance dimension in order to compare their edges. This is performed by convolving a 3 × 3 Sobel filter in both the horizontal and vertical directions of each image to get the corresponding gradients. The horizontal and vertical gradients are then collapsed to the gradient magnitude of each image using the Euclidean distance. 4 The similarity between the gradient magnitudes of the reference and distorted image are then com- pared using Equation 7. Third, Equation 7 is used to directly compute the similarity between the I and Q color dimensions of each image. The mean is then taken of the GMS score (resulting in the GMSM score) and the combined I and Q scores (resulting in the Chrom score). In order to experimentally evaluate how each of the different components contribute to the underly- ing image representations, we defined the following, multi-component energy function: E D = δ∈D δ(D(x), x)β d δ∈D β d (8) where β d is the weight that determines the proportion of each δ to include for a given model, and D includes the l 1 norm, GMSM, and the chrominance part of cQS as individual δs. In what follows, we experimentally evaluate each of the energy function components(β) and some of their combinations.\n\nSection Title: EXPERIMENTS\n EXPERIMENTS\n\nSection Title: METHOD\n METHOD We conducted extensive quantitative and qualitative evaluation on the CelebA dataset of face images Liu et al. (2015) . This dataset has been used frequently in the past for evaluating GANs Radford et al. (2015) ; Zhao et al. (2016) ; Chen et al. (2016) ; Liu & Tuzel (2016) . We evaluated 12 different models in a number of combinations (see Table 1 ). They are as follows. Models 1, 7, and 11 are the original BEGAN model. Models 2 and 3 only use the GMSM and chrominance distance functions, respectively. Models 4 and 8 are the BEGAN model plus GMSM. Models 5 and 9 use all three Under review as a conference paper at ICLR 2018 distance functions (BEGAN+GMSM+Chrom). Models 6, 10, and 12 use a 'scaled' BEGAN model (β l1 = 2) with GMSM. All models with different model numbers but the same β d values differ in their γ values or the output image size.\n\nSection Title: SETUP\n SETUP All of the models we evaluate in this paper are based on the architecture of the BEGAN model Berthelot et al. (2017) . 5 We trained the models using Adam with a batch size of 16, β 1 of 0.9, β 2 of 0.999, and an initial learning rate of 0.00008, which decayed by a factor of 2 every 100,000 epochs. Parameters k t and k 0 were set at 0.001 and 0, respectively (see Equation 5). The γ parameter was set relative to the model (see Table 1 ). Most of our experiments were performed on 64 × 64 pixel images with a single set of tests run on 128 × 128 images. The number of convolution layers were 3 and 4, respectively, with a constant down-sampled size of 8 × 8. We found that the original size of 64 for the input vector (N z ) and hidden state (N h ) resulted in modal collapse for the models using GMSM. However, we found that this was fixed by increasing the input size to 128 and 256 for the 64 and 128 pixel images, respectively. We used N z = 128 for all models except 12 (scaled BEGAN+GMSM), which used 256. N z always equaled N h in all experiments. Models 2-3 were run for 18,000 epochs, 1 and 4-10 were run for 100,000 epochs, and 11-12 were run for 300,000 epochs. Models 2-4 suffered from modal collapse immediately and 5 (BE- GAN+GMSM+Chrom) collapsed around epoch 65,000 (see Appendix A Figure 4 rows 2-5).\n\nSection Title: EVALUATIONS\n EVALUATIONS We performed two evaluations. First, to evaluate whether and to what extent the models were able to capture the relevant properties of each associated distance function, we compared the mean and standard deviation of the error scores. We calculated them for each distance function over all epochs of all models. We chose to use the mean rather than the minimum score as we were interested in how each model performs as a whole, rather than at some specific epoch. All calculations use the distance, or one minus the corresponding similarity score, for both the gradient magnitude and chrominance values. Reduced pixelation is an artifact of the intensive scaling for image presentation (up to 4×). All images in the qualitative evaluations were upscaled from their original sizes using cubic image sampling so that they can be viewed at larger sizes. Consequently, the apparent smoothness of the scaled images is not a property of the model.\n\nSection Title: RESULTS\n RESULTS GANs are used to generate different types of images. Which image components are important depends on the domain of these images. Our results suggest that models used in any particular GAN application should be customized to emphasize the relevant components-there is not a one-size- fits-all component choice. We discuss the results of our four evaluations below.\n\nSection Title: MEANS AND STANDARD DEVIATIONS OF ERROR SCORES\n MEANS AND STANDARD DEVIATIONS OF ERROR SCORES Results were as expected: the three different distance functions captured different features of the underlying image representations. We compared all of the models in terms of their means and standard deviations of the error score of the associated distance functions (see Table 2 ). In particular, each of models 1-3 only used one of the distance functions and had the lowest error for the associated function (e.g., model 2 was trained with GMSM and has the lowest GMSM error score). Models 4-6 expanded on the first three models by examining the distance functions in different combinations. Model 5 (BEGAN+GMSM+Chrom) had the lowest chrominance error score and Model 6 (scaled BEGAN+GMSM) had the lowest scores for l 1 and GMSM of any model using a γ of 0.5. For the models with γ set at 0.7, models 7-9 showed similar results to the previous scores. Model 8 (BEGAN+GMSM) scored the lowest GMSM score overall and model 9 (BEGAN+GMSM+Chrom) scored the lowest chrominance score of the models that did not suffer from modal collapse. For the two models that were trained to generate 128 × 128 pixel images, model 12 (scaled BE- GAN+GMSM) had the lowest error scores for l 1 and GMSM, and model 11 (BEGAN) had the lowest score for chrominance. Model 12 had the lowest l 1 score, overall.\n\nSection Title: VISUAL COMPARISON OF SIMILARITY SCORES\n VISUAL COMPARISON OF SIMILARITY SCORES Subjective visual comparison of the gradient magnitudes in column S of Figure 2 shows there are more black pixels for model 11 (row 11D) when comparing real images before and after autoencod- ing. This indicates a lower similarity in the autoencoder. Model 12 (row 12D) has a higher similarity between the original and autoencoded real images as indicated by fewer black pixels. This pattern continues for the generator output (rows 11G and 12G), but with greater similarity between the gra- dients of the original and autoencoded images than the real images (i.e., fewer black pixels overall). The visual comparison of chrominance and related similarity score also weakly supported our hy- potheses (see Figure 3 ). All of the models show a strong ability to capture the I dimension (blue-red) of the YIQ color space, but only model 9 (BEGAN+GMSM+Chrom) is able to accurately capture the relevant information in the Q dimension (green-purple).\n\nSection Title: OUTLOOK\n OUTLOOK We bring an energy-based formulation to the BEGAN model and some of the problems of the en- ergy function originally proposed in Zhao et al. (2016) . We proposed a new, multi-component energy function on the basis of research from the Image Quality Assessment literature. The scaled BEGAN+GMSM model produces better image representations than its competitors in ways that can be measured using subjective evaluations of the associated features (e.g., luminance gradient simi- larity, chrominance similarity). For future work, we would like to extend this research to encompass other datasets and FR-IQA energy functions.\n\nSection Title: Annex Figures\n Annex Figures fig_3 Figure 4: Figure 4: Four outputs of each of the generators of all 12 models. The best images for each model were hand-picked. The first row is model 1, which corresponds with the original BEGAN model. Rows 2-12 represent our experiments. Each cell represents the output of a random sample. \n"}, {"role": "assistant", "content": "[Significance and novelty]\n<Incremental nature of the paper> Reviewers highlighted that the paper's proposed approach was somewhat incremental, and its significance and novelty were questioned. The modifications and additions to the existing BEGAN framework were not perceived as significantly contributing to the field.\n<Limited novelty of energy function components> The paper's novelty was deemed to be restricted, particularly in the choice and justification of the energy function components. Reviewers pointed out that the selected components were borrowed from existing image quality assessment techniques, and their application was not seen as a significant contribution to GAN theories or algorithm designs.\n\n[Potential reasons for acceptance]\n<No related terms> -\n\n[Potential reasons for rejection]\n<Weak experiments and results analysis> Reviewers noted that the experimental section was weak, with reliance on visual evaluations and a limited range of datasets (primarily CelebA). This led to concerns about the thoroughness and robustness of the paper's findings.\n<Unclear significance and contribution> The paper was criticized for its lack of clarity in motivating its contributions and presenting results. Reviewers found it difficult to estimate the significance of the proposed model and understand how its results differed from baseline models.\n\n[Suggestions for improvement]\n<Broaden experimental testing> To strengthen the paper, reviewers suggested broadening the experimental testing to include different datasets involving natural images, beyond the single CelebA dataset. This would provide a more comprehensive evaluation of the proposed techniques.\n<Clarify and justify design choices> Improvements in the paper's clarity and justification were recommended, specifically in clarifying the design choices made for the energy function components. Providing clear justifications for the modifications and additions to the BEGAN framework would enhance the paper's credibility and significance.\n\n"}]} {"messages": [{"role": "system", "content": "You are a professional machine learning conference reviewer who reviews a given paper and considers 4 criteria: ** importance and novelty **, ** potential reasons for acceptance **, ** potential reasons for rejection **, and ** suggestions for improvement **. \nThe given paper is as follows."}, {"role": "user", "content": "[TITLE]\nSimulating Action Dynamics with Neural Process Networks\n\n[ABSTRACT]\nUnderstanding procedural language requires anticipating the causal effects of actions, even when they are not explicitly stated. In this work, we introduce Neural Process Networks to understand procedural text through (neural) simulation of action dynamics. Our model complements existing memory architectures with dynamic entity tracking by explicitly modeling actions as state transformers. The model updates the states of the entities by executing learned action operators. Empirical results demonstrate that our proposed model can reason about the unstated causal effects of actions, allowing it to provide more accurate contextual information for understanding and generating procedural text, all while offering more interpretable internal representations than existing alternatives.\n\n[CAPTIONS]\nFigure 1: The process is a narrative of entity state changes induced by actions. In each sen- tence, these state changes are induced by simu- lated actions and must be remembered.\nFigure 2: Model Summary. The sentence encoder converts a sentence to a vector representation, ht. The action selector and entity selector use the vector representation to choose the actions that are applied and the entities that are acted upon in the sentence. The simulation module indexes the action and entity state embeddings, and applies the transformation to the entities. The state predictors predict the new state of the entities if a state change has occurred. Equation references are provided in parentheses.\nFigure 3: Change in cosine similarity of entity state embeddings\nTable 1: Example actions, the state changes they induce, and the possible end states\nTable 2: Results for entity selection and state change selection tions, entity selection and end state prediction, and also investigate whether the model learns internal representations that approximate recipe dynamics.\nTable 3: Examples of the model selecting entities for sentence s t . The previous sentences are provided as context in cases where they are relevant.\nTable 4: Most similar actions based on cosine sim- ilarity of action embeddings\nTable 5: Generation Results as compositional entities (Ex. 1, 3), and elided arguments over long time windows (Ex. 2). We also provide examples where the model fails to select the correct entities because it does not identify the mapping between a reference construct such as \"pizza\" (Ex. 4) or \"dough\" (Ex. 5) and the set of entities that composes it, showcasing the difficulty of selecting the full set for a composed entity.\nTable 6: Examples of the model generating sentences compared to baselines. The context and reference are provided first, followed by our model's generation and then the baseline generations showing that the NPN generator can use information about ingredient states to reason about the most likely next step. The first and second examples are interesting as it shows that the NPN-aware model has learned to condition on entity state - knowing that raw butter will likely be melted or that a cooked flan must be refrigerated. The third example is also interesting because the model learns that cooked vegetables such as squash will sometimes be drained, even if it is not relevant to this recipe because the squash is steamed. The seq2seq and EntNet baselines, meanwhile, output reasonable sentences given the immediate context, but do not exhibit understanding of global patterns.\n\n[CONTENT]\nSection Title: INTRODUCTION\n INTRODUCTION Understanding procedural text such as instructions or stories requires anticipating the implicit causal effects of actions on entities. For example, given instructions such as \"add blueberries to the muf- fin mix, then bake for one half hour,\" an intelligent agent must be able to anticipate a number of entailed facts (e.g., the blueberries are now in the oven; their \"temperature\" will increase). While this common sense reasoning is trivial for humans, most natural language understanding algorithms do not have the capacity to reason about causal effects not mentioned directly in the surface strings (Levy et al., 2015; Jia & Liang, 2017; Lucy & Gauthier, 2017). In this paper, we introduce Neural Process Net- works, a procedural language understanding sys- tem that tracks common sense attributes through neural simulation of action dynamics. Our net- work models interpretation of natural language instructions as a process of actions and their cu- mulative effects on entities. More concretely, reading one sentence at a time, our model atten- tively selects what actions to execute on which entities, and remembers the state changes in- duced with a recurrent memory structure. In Figure 1 , for example, our model indexes the \"tomato\" embedding, selects the \"wash\" and \"cut\" functions and performs a computation that changes the \"tomato\" embedding so that it can reason about attributes such as its \"SHAPE\" and \"CLEANLINESS\". Our model contributes to a recent line of research that aims to model aspects of world state changes, such as language models and machine readers with explicit entity representations (Henaff et al., 2016; Yang et al., 2016; Ji et al., 2017), as well as other more general purpose memory network variants (Weston et al., 2014; Sukhbaatar et al., 2015; Hill et al., 2015; Seo et al., 2016). This world- centric modeling of procedural language (i.e., understanding by simulation) abstracts away from the surface strings, complementing text-centric modeling of language, which focuses on syntactic and semantic labeling of surface words (i.e., understanding by labeling). Unlike previous approaches, however, our model also learns explicit action representations as func- tional operators (See Figure 1 ). While representations of action semantics could be acquired through an embodied agent that can see and interact with the world (Oh et al., 2015), we propose to learn these representations from text. In particular, we require the model to be able to explain the causal effects of actions by predicting natural language attributes about entities such as \"LOCATION\" and \"TEMPERATURE\". The model adjusts its representations of actions based on errors it makes in pre- dicting the resultant state changes to attributes. This textual simulation allows us to model aspects of action causality that are not readily available in existing simulation environments. Indeed, most virtual environments offer limited aspects of the world - with a primary focus on spatial relations (Oh et al., 2015; Chiappa et al., 2017; Wahlstrom et al., 2015). They leave out various other dimen- sions of the world states that are implied by diverse everyday actions such as \"dissolve\" (change of \"COMPOSITION\") and \"wash\" (change of \"CLEANLINESS\"). Empirical results demonstrate that parametrizing explicit action embeddings provides an inductive bias that allows the neural process network to learn more informative context representations for understanding and generating natural language procedural text. In addition, our model offers more interpretable internal representations and can reason about the unstated causal effects of actions explained through natural language descriptors. Finally, we include a new dataset with fine-grained annotations on state changes, to be shared publicly, to encourage future research in this direction.\n\nSection Title: NEURAL PROCESS NETWORK\n NEURAL PROCESS NETWORK The neural process network is an interpreter that reads in natural language sentences, one at a time, and simulates the process of actions being applied to relevant entities through learned representations of actions and entities.\n\nSection Title: OVERVIEW AND NOTATION\n OVERVIEW AND NOTATION The main component of the neural process network is the simulation module (§2.5), a recurrent unit whose internals simulate the effects of actions being applied to entities. A set of V actions is known a priori and an embedding is initialized for each one, F = {f 1 , ...f V }. Similarly, a set of I entities is known and an embedding is initialized for each one: E = {e 1 , ...e I }. Each e i can be considered to encode information about state attributes of that entity, which can be extracted by a set of state predictors (§2.6). As the model reads text, it \"applies\" action embeddings to the entity vectors, thereby changing the state information encoded about the entities. For any document d, an initial list of entities I d is known and E d = {e i |i ∈ I d } ⊂ E entity state embeddings are initialized. As the neural process network reads a sentence from the document, it selects a subset of both F (§2.3) and E d (§2.4) based on the actions performed and entities affected in the sentence. The entity state embeddings are changed by the action and the new embeddings are used to predict end states for a set of state changes (§2.6). The prediction error for end states is backpropagated to the action embeddings, learning action representations that model the simulation of desired causal effects on entities. This process is broken down into five modules below. Unless explicitly defined, all W and b variables are parametrized linear projections and biases. We use the notation {e i } t when referring to the values of the entity embeddings before processing sentence s t .\n\nSection Title: SENTENCE ENCODER\n SENTENCE ENCODER Given a sentence s t , a Gated Recurrent Unit (Cho et al., 2014) encodes each word and outputs its last hidden vector as a sentence encoding h t (Sutskever et al., 2014).\n\nSection Title: ACTION SELECTOR\n ACTION SELECTOR Given h t from the sentence encoder, the action selector (bottom left in Fig. 2 ) contextually deter- mines which action(s) from F to execute. For example, if the input sentence is \"wash and cut beets\", both f wash and f cut must be selected. To account for multiple actions, we make a soft selection over F, yielding a weighted sum of the selected action embeddingsf t : w p = MLP(h t ) w p = w p V j=1 w pj f t =w p F (1) where MLP is a parametrized feed-forward network with a sigmoid activation and w p ∈ R V is the attention distribution over V possible actions (§3.1). We compose the action embedding by taking the weighted average of the selected actions.\n\nSection Title: ENTITY SELECTOR\n ENTITY SELECTOR Sentence Attention Given h t from the sentence encoder, the entity selector chooses relevant en- tities using a soft attention mechanism: where W 2 is a bilinear mapping, e i0 is a unique key for each entity (§2.5), and d i is the attention weight for entity embedding e i . For example, in \"wash and cut beets and carrots\", the model should select e beet and e carrot .\n\nSection Title: Recurrent Attention\n Recurrent Attention While sentence attention would suffice if entities were always explicitly mentioned, natural language often elides arguments or uses referent pronouns. As such, the module must be able to consider entities mentioned in previous sentences. Usingh t , the model computes a soft choice over whether to choose affected entities from this step's attention d i or the previous step's attention distribution. where c ∈ R 3 is the choice distribution, a it−1 is the previous sentence's attention weight for each entity, a it is the final attention for each entity, and 0 is a vector of zeroes (providing the option to not change any entity). Prior entity attentions can propagate forward for multiple steps.\n\nSection Title: SIMULATION MODULE\n SIMULATION MODULE Entity Memory A unique state embedding e i is initialized for every entity i in the document. A unique key to index each embedding e i0 is set as the initial value of the embedding (Henaff et al., 2016; Miller et al., 2016). After the model reads s t , it modifies {e i } t to reflect changes influenced by actions. At every time step, the entity memory receives the attention weights from the entity selector, normalizes them and computes a weighted average of the relevant entity state embeddings: Applicator Given the action summary embeddingf t and the entity summary embeddingē t , the applicator (middle right in Fig. 2 ) applies the selected actions to the selected entities, and outputs the new proposal entity embedding k t . k t = ReLU(f t W 4ēt + b 4 ) (6) where W 4 is a third order tensor projection. The vector k t is the new representation of the entityē t after the applicator simulates the action being applied to it.\n\nSection Title: Entity Updater\n Entity Updater The entity updater interpolates the new proposal entity embedding k t and the set of current entity embeddings {e i } t : e it+1 = a it k t + (1 − a it )e it (7) yielding an updated set of entity embeddings {e i } t+1 . Each embedding is updated proportional to its entity's unnormalized attention a i , allowing the model to completely overwrite the state embedding for any entity. For example, in the sentence \"mix the flour and water,\" the embeddings for e f lour and e water must both be overwritten by k t because they no longer exist outside of this new composition.\n\nSection Title: STATE PREDICTORS\n STATE PREDICTORS Given the new proposal entity embedding k t , the state predictor (bottom right in Fig. 2 ) predicts changes to the resulting entity embedding k t along the following six dimensions: location, cooked- ness, temperature, composition, shape, and cleanliness. Discrete multi-class classifiers, one for each dimension, take in k t and predict a unique end state for their corresponding state change type: For location changes, which require contextual information to predict the end state, k t is concate- nated with the original sentence representation h t to predict the final state.\n\nSection Title: TRAINING\n TRAINING\n\nSection Title: STATE CHANGE KNOWLEDGE\n STATE CHANGE KNOWLEDGE In this work we focus on physical action verbs in cooking recipes. We manually collect a set of 384 actions such as cut, bake, boil, arrange, and place, organizing their causal effects along the following predefined dimensions: LOCATION, COOKEDNESS, TEMPERATURE, SHAPE, CLEANLI- NESS and COMPOSITION. The textual simulation operated by the model induces state changes along these dimensions by applying actions functions from the above set of 384. For example, cut entails a change in SHAPE, while bake entails a change in TEMPERATURE, COOKEDNESS, and even LO- CATION. We annotate the state changes each action induces, as well as the end state of the action, using Amazon Mechanical Turk. The set of possible end states for a state change can range from 2 for binary state changes to more than 200 (See Appendix C for details). Table 1 provides examples of annotations in this action lexicon.\n\nSection Title: DATASET\n DATASET For learning and evaluation, we use a subset of the Now You're Cooking dataset (Kiddon et al., 2016). We chose 65816 recipes for training, 175 recipes for development, and 700 recipes for testing. For the development and test sets, crowdsourced workers densely annotate actions, entities and state changes that occur in each sentence so that we can tune hyperparameters and evaluate on gold evaluation sets. Annotation details are provided in Appendix C.3.\n\nSection Title: COMPONENT-WISE TRAINING\n COMPONENT-WISE TRAINING The neural process network is trained by jointly optimizing multiple losses for the action selector, entity selector, and state change predictors. Importantly, our training scheme uses weak supervision because dense annotations are prohibitively expensive to acquire at a very large scale. Thus, we heuristically extract verb mentions from each recipe step and assign a state change label based on the state changes induced by that action (§3.1). Entities are extracted similarly based on string matching between the instructions and the ingredient list. We use the following losses for training: Action Selection Loss Using noisy supervision, the action selector is trained to minimize the cross-entropy loss for each possible action, allowing multiple actions to be chosen at each step if multiple actions are mentioned in a sentence. The MLP in the action selector (Eq. 1) is pretrained. Entity Selection Loss Similarly, to train the attentive entity selector, we minimize the binary cross-entropy loss of predicting whether each entity is affected in the sentence. State Change Loss For each state change predictor, we minimize the negative loglikelihood of predicting the correct end state for each state change.\n\nSection Title: Coverage Loss\n Coverage Loss An underlying assumption in many narratives is that all entities that are mentioned should be important to the narrative. We add a loss term that penalizes narratives whose combined attention weights for each entity does not sum to more than 1. L cover = − 1 I d I d i=1 log S t=1 a it (9) where a it is the attention weight for a particular entity at sentence t and I d is the number of entities in a document. S t=1 a it is upper bounded by 1. This is similar to the coverage penalty used in neural machine translation (Tu et al., 2016).\n\nSection Title: EXPERIMENTAL SETUP\n EXPERIMENTAL SETUP We evaluate our model on a set of intrinsic tasks centered around tracking entities and state changes in recipes to show that the model can simulate preliminary dynamics of the recipe task. Additionally, we provide a qualitative analysis of the internal components of our model. Finally, we evaluate the quality of the states encoded by our model on the extrinsic task of generating future steps in a recipe.\n\nSection Title: INTRINSIC EVALUATION - TRACKING\n INTRINSIC EVALUATION - TRACKING In the tracking task, we evaluate the model's ability to identify which entities are selected and what changes have been made to them in every step. We break the tracking task into two separate evalua-\n\nSection Title: Metrics\n Metrics In the entity selection test, we report the F1 score of choosing the correct entities in any step. A selected entity is defined as one whose attention weight a i is greater than 50% (§2.4). Because entities may be harder to predict when they have been combined with other entities (e.g., the mixture may have a new name), we also report the recall for selecting combined (CR) and uncombined (UR) entities. In the end state prediction test, we report how often the model correctly predicts the state change performed in a recipe step and the resultant end state. This score is then scaled by the accuracy of predicting which entities were changed in that same step. We report the average F1 and accuracy across the six state change types.\n\nSection Title: Baselines\n Baselines We compare our models against two baselines. First, we built a GRU model that is trained to predict entities and state changes independently. This can be viewed as a bare minimum network with no action representations or recurrent entity memory. The second baseline is a Re- current Entity Network (Henaff et al., 2016) with changes to fit our task. First, the model can tie memory cells to a subset of the full list of entities so that it only considers entities that are present in a particular recipe. Second, the entity distribution for writing to the memory cells is re-used when we query the memory cells. The normalized weighted average of the entity cells is used as the in- put to the state predictors. The unnormalized attention when writing to each cell is used to predict selected entities. Both baselines are trained with entity selection and state change losses (§3.3).\n\nSection Title: Ablations\n Ablations We report results on six ablations. First, we remove the recurrent attention (Eq. 3). The model only predicts entities using the current encoder hidden state. In the second ablation, the model is trained with no coverage penalty (Eq. 9). The third ablation prunes the connection from the action selector w p to the entity selector (Eq. 2). We also explore not pretraining the action selector. Finally, we look at two ablations where we intialize the action embeddings with vectors from a skipgram model. In the first, the model operates normally, and in the second, we do not allow gradients to backpropagate to the action embeddings, updating only the mapping tensor W 4 instead (Eq. 6).\n\nSection Title: EXTRINSIC EVALUATION - GENERATION\n EXTRINSIC EVALUATION - GENERATION The generation task tests whether our system can produce the next step in a recipe based on the previous steps that have been performed. The model is provided all of the previous steps as context.\n\nSection Title: Metrics\n Metrics We report the combined BLEU score and ROUGE score of the generated sequence rela- tive to the reference sequence. Each candidate sequence has one reference sentence. Both metrics are computed at the corpus-level. Also reported are \"VF1\", the F1 score for the overlap of the ac- tions performed in the reference sequence and the verbs mentioned in the generated sequence, and \"SF1\", the F1 score for the overlap of end states annotated in the reference sequence and predicted by the generated sequences. End states for the generated sequences are extracted using the lexicon from Section 3.1 based on the actions performed in the sentence.\n\nSection Title: Setup\n Setup been read (§2.5). These vectors can be viewed as a snapshot of the current state of the entities once the preceding context has been simulated inside the neural process network. We encode these vectors using a bidirectional GRU (Cho et al., 2014) and take the final time step hidden state e I . A different GRU encodes the context words in the same way (yielding h T ) and the first hidden state input to the decoder is computed using the projection function: h 0 = W 5 (e I • h T ) (10) where • is the Hadamard product between the two encoder outputs. All models are trained by mini- mizing the negative loglikelihood of predicting the next word for the full sequence. Implementation details can be found in Appendix A.\n\nSection Title: Baselines\n Baselines For the generation task, we use three baselines: a seq2seq model with no attention (Sutskever et al., 2014), an attentive seq2seq model (Bahdanau et al., 2014), and a similar variant as our NPN generator, except where the entity states have been computed by the Recurrent Entity Network (EntNet) baseline (§4.1). Implementation details for baselines can be found in Appendix B.\n\nSection Title: EXPERIMENTAL RESULTS\n EXPERIMENTAL RESULTS\n\nSection Title: INTRINSIC EVALUATIONS\n INTRINSIC EVALUATIONS\n\nSection Title: Entity Selection\n Entity Selection As shown in Table 8, our full model outperforms all baselines at selecting enti- ties, with an F1 score of 55.39%. The ablation study shows that the recurrent attention, coverage loss, action connections and action selector pretraining improve performance. Our success at pre- dicting entities extends to both uncomposed entities, which are still in their raw forms (e.g., melt the butter → butter), and composed entities, in which all of the entities that make up a composition must be selected. For example, in a Cooking lasagna recipe, if the final step involves baking the prepared lasagna, the model must select all the entities that make up the lasagna (e.g., lasagna sheets, beef, tomato sauce). In Table 3 , we provide examples of our model's ability to handle complex cases such Action Nearest Neighbor Actions cut slice, split, snap, slash, carve, slit, chop boil cook, microwave, fry, steam, simmer add sprinkle, mix, reduce, splash, stir, dust wash rinse, scrub, refresh, soak, wipe, scale mash spread, puree, squeeze, liquefy, blend place ease, put, lace, arrange, leave rinse wash, refresh, soak, wipe, scrub, clean warm reheat, ignite, heat, light, crisp, preheat steam microwave, crisp, boil, parboil, heat sprinkle top, pat, add, dip, salt, season grease coat, rub, dribble, spray, smear, line\n\nSection Title: State Change Tracking\n State Change Tracking In Table 8, we show that our full model outperforms competitive base- lines such as Recurrent Entity Networks (Henaff et al., 2016) and jointly trained GRUs. While the ablation without the coverage loss shows higher accuracy, we attribute this to the fact that it predicts a smaller number of total state changes. Interestingly, initializing action embeddings with skipgram vectors and locking their values shows relatively high performance, indicating the potential gains in using powerful pretrained representations to represent actions.\n\nSection Title: Action Embeddings\n Action Embeddings In our model, each action is assigned its own embedding, but many actions induce similar changes in the physical world (e.g.,\"cut\" and \"slice\"). After training, we compute the pairwise cosine similarity between each pair of action embeddings. In Table 4 , we see that actions that perform similar functions are neighbors in embedding space, indicating the model has captured certain semantic properties of these actions. Learning action representations through the state changes they induce has allowed the model to cluster actions by their transformation functions.\n\nSection Title: Entity Compositions\n Entity Compositions When individual entities are combined into new constructs, our model av- erages their state embeddings (Eq. 5), applies an action embedding to them (Eq. 6), and writes them to memory (Eq. 7). The state embeddings of entities that are combined should be overwritten by the same new embedding. In Figure 3 , we present the percentage increase in cosine similarity for state embeddings of entities that are combined in a sentence (blue) as opposed to the percentage increase for those that are not (red bars). While the soft attention mechanism for entity selection allows similarities to leak between entity embeddings, our system is generally able to model the compositionality patterns that result from entities being combined into new constructs.\n\nSection Title: EXTRINSIC EVALUATIONS\n EXTRINSIC EVALUATIONS\n\nSection Title: Recipe Step Generation\n Recipe Step Generation Our results in Table 5 indicate that sequences generated using the neural process network entity states as additional input yield higher scores than competitive baselines. The entity states allow the model to predict next steps conditioned on a representation of the world being simulated by the neural process network. Additionally, the higher VF1 and SF1 scores indicate that the model is indeed using the extra information to better predict the actions that should follow the context provided. Example generations for each baselines from the dev set are provided in Table 6 ,\n\nSection Title: RELATED WORK\n RELATED WORK Recent studies in machine comprehension have used a neural memory component to store a running representation of processed text (Weston et al., 2014; Sukhbaatar et al., 2015; Hill et al., 2015; Seo et al., 2016). While these approaches map text to memory vectors using standard neural encoder approaches, our model, in contrast, directly interprets text in terms of the effects actions induce in entities, providing an inductive bias for learning how to represent stored memories. More recent work in machine comprehension also sought to couple the memory representation with tracking en- tity states (Henaff et al., 2016). Our work seeks to provide a relatively more structured representation of domain-specific action knowledge to provide an inductive bias to the reasoning process. Neural Programmers (Neelakantan et al., 2015; 2016) have also used functions to simulate reason- ing, by building a model to select rows in a database and applying operation on those selected rows. While their work explicitly defined the effect of a number of operations for those rows, we provide a framework for learning representations for a more expansive set of actions, allowing the model to learn representations for how actions change the state space. Works on instructional language studied the task of building discrete graph representations of recipes using probabilistic models (Kiddon et al., 2015; Mori et al., 2014; 2012). We propose a complemen- tary new model by integrating action and entity relations into the neural network architecture and also address the additional challenge of tracking the state changes of the entities. Additional work in tracking states with visual or multimodal context has focused on 1) building graph representations for how entities change in goal-oriented domains (Gao et al., 2016; Liu et al., 2016; Si et al., 2011) or 2) tracking visual state changes based on decisions taken by agents in environment simulators such as videos or games (Chiappa et al., 2017; Wahlstrom et al., 2015; Oh et al., 2015). Our work, in contrast, models state changes in embedding space using only text-based signals to map real-world actions to algebraic transformations.\n\nSection Title: CONCLUSION\n CONCLUSION We introduced the Neural Process Network for modeling a process of actions and their causal ef- fects on entities by learning action transformations that change entity state representations. The model maintains a recurrent memory structure to track entity states and is trained to predict the state changes that entities undergo. Empirical results demonstrate that our model can learn the causal effects of action semantics in the cooking domain and track the dynamic state changes of entities, showing advantages over competitive baselines.\n"}, {"role": "assistant", "content": "[Significance and novelty]\n<No related terms> -\n\n[Potential reasons for acceptance]\n<Thoroughness of the proposed approach and justification> The reviewers acknowledge the thoroughness of the proposed approach and the authors' justification, recommending its acceptance.\n<Use of a weakly supervised learning approach> The weakly supervised learning approach employed by the model is considered interesting and indicative of the model introducing the suitable bias to produce better results.\n\n[Potential reasons for rejection]\n<Concerns about generalizability> Reviewers expressed concerns about the generalizability of the proposed model, particularly in terms of its applicability to other tasks beyond the specific focus of the paper.\n<Lack of thorough qualitative analysis> There are concerns about the qualitative analysis of the results, particularly in terms of potential cherry-picking of examples and the need for a more comprehensive discussion of failure cases.\n\n[Suggestions for improvement]\n<Comprehensive qualitative analysis> The paper would benefit from a more comprehensive qualitative analysis, including a discussion of failure cases and a more thorough exploration of the model's performance on a range of examples.\n<Discussion on generalizability and applicability of the model> The authors should provide more clarity on the generalizability and applicability of the model beyond the specific tasks presented in the paper, addressing potential limitations and areas for future research.\n\n"}]} {"messages": [{"role": "system", "content": "You are a professional machine learning conference reviewer who reviews a given paper and considers 4 criteria: ** importance and novelty **, ** potential reasons for acceptance **, ** potential reasons for rejection **, and ** suggestions for improvement **. \nThe given paper is as follows."}, {"role": "user", "content": "[TITLE]\nBounding and Counting Linear Regions of Deep Neural Networks\n\n[ABSTRACT]\nIn this paper, we study the representational power of deep neural networks (DNN) that belong to the family of piecewise-linear (PWL) functions, based on PWL activation units such as rectifier or maxout. We investigate the complexity of such networks by studying the number of linear regions of the PWL function. Typically, a PWL function from a DNN can be seen as a large family of linear functions acting on millions of such regions. We directly build upon the work of Mont´ufar et al. (2014), Mont´ufar (2017), and Raghu et al. (2017) by refining the upper and lower bounds on the number of linear regions for rectified and maxout networks. In addition to achieving tighter bounds, we also develop a novel method to perform exact numeration or counting of the number of linear regions with a mixed-integer linear formulation that maps the input space to output. We use this new capability to visualize how the number of linear regions change while training DNNs. \n\n[CAPTIONS]\nFigure 1: (a) Simple DNN with two inputs and three hidden layers with 2 activation units each. (b), (c), and (d) Visualization of the hyperplanes from the first, second, and third hidden layers respec- tively partitioning the input space into several linear regions. The arrows indicate the directions in which the corresponding neurons are activated. (e), (f), and (g) Visualization of the hyperplanes from the first, second, and third hidden layers in the space given by the outputs of their respective previous layers.\nFigure 2: (a) A network with one input x 1 and three activation units a, b, and c. (b) We show the hyperplanes x 1 = 0 and −x 1 + 1 = 0 corresponding to the two activation units in the first hidden layer. In other words, the activation units are given by h a = max{0, x 1 } and h b = max{0, −x 1 + 1}. (c) The activation unit in the third layer is given by h c = max{0, 4h a + 2h b − 3}. (d) The activation boundary for neuron c is disconnected.\nFigure 3: Bounds from Theorem 1: (a) is in semilog scale, has input dimension n 0 = 32, and the width of the first five layers is 16 − 2k, 16 − k, 16, 16 + k, 16 + 2k; (b) is in linear scale, evenly distributes 60 neurons in 1 to 6 layers (the single-layer case is exact), and the input dimension varies.\nFigure 4: Total number of regions classifying each digit (different colors for 0-9) of MNIST alone as training progresses, each plot corresponding to a different number of hidden layers.\nFigure 5: (a) Total number of linear regions classifying a single digit of MNIST as training pro- gresses, each plot corresponding to a different number of hidden layers. (b) Comparison of upper bounds from Montúfar et al. (2014), Montúfar (2017), and from Theorem 1 with the total number of linear regions of a network with two hidden layers totaling 22 neurons.\n\n[CONTENT]\nSection Title: INTRODUCTION\n INTRODUCTION We have witnessed an unprecedented success of deep learning algorithms in computer vision, speech, and other domains ( Krizhevsky et al., 2012 ; Ciresan et al., 2012 ; Goodfellow et al., 2013 ; Hinton et al., 2012 ). While the popular deep learning architectures such as AlexNet ( Krizhevsky et al., 2012 ), GoogleNet ( Szegedy et al., 2015 ), and residual networks ( He et al., 2016 ) have shown record beating performance on various image recognition tasks, empirical results still govern the design of network architecture in terms of depth and activation functions. Two important practical considerations that are part of most successful architectures are greater depth and the use of PWL activation functions such as rectified linear units (ReLUs). Due to the large gap between theory and practice, many researchers have been looking at the theoretical modeling of the representational power of DNNs ( Cybenko, 1989 ; Anthony & Bartlett, 1999 ; Pascanu et al., 2014 ; Montúfar et al., 2014 ; Bianchini & Scarselli, 2014 ; Eldan & Shamir, 2016 ; Telgarsky, 2015 ; Mhaskar et al., 2016 ; Raghu et al., 2017 ; Montúfar, 2017 ). Any continuous function can be approximated to arbitrary accuracy using a single hidden layer of sigmoid activation functions ( Cybenko, 1989 ). This does not imply that shallow networks are sufficient to model all problems in practice. Typically, shallow networks require exponentially more number of neurons to model functions that can be modeled using much fewer activation functions in deeper ones ( Delalleau & Bengio, 2011 ). There have been a wide variety of activation functions such as threshold (f (z) = (z > 0)), logistic (f (z) = 1/(1 + exp(−e))), hyperbolic tangent (f (z) = tanh(z)), rectified linear units (ReLUs f (z) = max{0, z}), and maxouts (f (z 1 , z 2 , . . . , z k ) = max{z 1 , z 2 , . . . , z k }). The activation functions offer different modeling capabilities. For example, sigmoid networks are shown to be more expressive than similar-sized threshold networks ( Maass et al., 1994 ). It was recently shown that ReLUs are more expressive than similar-sized threshold networks by deriving transformations from one network to another ( Pan & Srikumar, 2016 ). The complexity of neural networks belonging to the family of PWL functions can be analyzed by looking at how the network can partition the input space to an exponential number of linear response regions ( Pascanu et al., 2014 ; Montúfar et al., 2014 ). The basic idea of a PWL function is simple: we can divide the input space into several regions and we have individual linear functions for each of these regions. Functions partitioning the input space to a larger number of linear regions are considered to be more complex ones, or in other words, possess better representational power. In the case of ReLUs, it was shown that deep networks separate their input space into exponentially more linear response regions than their shallow counterparts despite using the same number of activation functions ( Pascanu et al., 2014 ). The results were later extended and improved ( Montúfar et al., 2014 ; Raghu et al., 2017 ; Montúfar, 2017 ; Arora et al., 2016 ). In particular, Montúfar et al. (2014) shows both upper and lower bounds on the maximal number of linear regions for a ReLU DNN and a single layer maxout network, and a lower bound for a maxout DNN. Furthermore, Raghu et al. (2017) and Montúfar (2017) improve the upper bound for a ReLU DNN. This upper bound asymptotically matches the lower bound from Montúfar et al. (2014) when the number of layers and input dimension are constant and all layers have the same width. Finally, Arora et al. (2016) improves the lower bound by providing a family of ReLU DNNS with an exponential number of regions given fixed size and depth. In this work, we directly improve on the results of Montúfar et al. ( Pascanu et al., 2014 ; Montúfar et al., 2014 ; Montúfar, 2017 ) and Raghu et al. ( Raghu et al., 2017 ) in better understanding the representational power of DNNs employing PWL activation functions.\n\nSection Title: NOTATIONS AND BACKGROUND\n NOTATIONS AND BACKGROUND We will only consider feedforward neural networks in this paper. Let us assume that the network has n 0 input variables given by x = {x 1 , x 2 , . . . , x n0 }, and m output variables given by y = {y 1 , y 2 , . . . , y m }. Each hidden layer l = {1, 2, . . . , L} has n l hidden neurons whose activations are given by h l = {h l 1 , h l 2 , . . . , h l n l }. Let W l be the n l × n l−1 matrix where each row corresponds to the weights of a neuron of layer l. Let b l be the bias vector used to obtain the activation functions of neurons in layer l. Based on the ReLU(x) = max{0, x} activation function, the activations of the hidden neurons and the outputs are given below: As considered in Pascanu et al. (2014) , the output layer is a linear layer that computes the linear combination of the activations from the previous layer without any ReLUs. We can treat the DNN as a piecewise linear (PWL) function F : R n0 → R m that maps the input x in R n0 to y in R m . This paper primarily deals with investigating the bounds on the linear regions of this PWL function. There are two subtly different definitions for linear regions in the literature and we will formally define them. Definition 1. Given a PWL function F : R n0 → R m , a linear region is defined as a maximal connected subset of the input space R n0 , on which F is linear ( Pascanu et al., 2014 ; Montúfar et al., 2014 ). Activation Pattern: Let us consider an input vector x = {x 1 , x 2 , . . . , x n0 }. For every layer l we define an activation set S l ⊆ {1, 2, . . . , n l } such that e ∈ S l if and only if the ReLU e is active, that is, h l e > 0. We aggregate these activation sets into a set S = (S 1 , . . . , S l ), which we call an activation pattern. Note that we may consider activation patterns up to a layer l ≤ L. Activation patterns were previously defined in terms of strings ( Raghu et al., 2017 ; Montúfar, 2017 ). We say that an input x corresponds to an activation pattern S in a DNN if feeding x to the DNN results in the activations in S. Definition 2. Given a PWL function F : R n0 → R m represented by a DNN, a linear region is the set of input vectors x that corresponds to an activation pattern S in the DNN. We prefer to look at linear regions as activation patterns and we interchangeably refer to S as an activation pattern or a region. Definitions 1 and 2 are essentially the same, except in a few degenerate cases. There could be scenarios where two different activation patterns may correspond to two adjacent regions with the same linear function. In this case, Definition 1 will produce only one linear region whereas Definition 2 will yield two linear regions. This has no effect on the bounds that we derive in this paper. In Fig. 1(a) we show a simple ReLU DNN with two inputs {x 1 , x 2 } and 3 hidden layers. The activation units {a, b, c, d, e, f } in the hidden layers can be thought of as hyperplanes that each divide the space in two. On one side of the hyperplane, the unit outputs a positive value. For all points on the other side of the hyperplane including itself, the unit outputs 0. One may wonder: into how many regions do n hyperplanes split a space? Zaslavsky (1975) shows that an arrangement of n hyperplanes divides a d-dimensional space into at most d s=0 n s regions, a bound that is attained when they are in general position. The term general position basically means that a small perturbation of the hyperplanes does not change the number of regions. This corresponds to the exact maximal number of regions of a single layer DNN with n ReLUs and input dimension d. In Figs. 1(b)-(g), we provide a visualization of how ReLUs partition the input space. Figs. 1(e), (f), and (g) show the hyperplanes corresponding to the ReLUs at layers l = 1, 2, and 3 respectively. Figs. 1(b), (c), and (d) consider these same hyperplanes in the input space x. In Fig. 1(b), as per Zaslavsky (1975) , the 2D input space is partitioned into 4 regions ( 2 0 + 2 1 + 2 2 = 4). In Figs. 1(c) and (d), we add the hyperplanes from the second and third layers respectively, which are affected by the transformations applied in the earlier hidden layers. The regions are further partitioned as we consider additional layers. Fig. 1 also highlights that activation boundaries behave like hyperplanes when inside a region and may bend whenever they intersect with a boundary from a previous layer. This has also been pointed out by Raghu et al. (2017) . In particular, they cannot appear twice in the same region as they are defined by a single hyperplane if we fix the region. Moreover, these boundaries do not need to be connected, as illustrated in Fig. 2 .\n\nSection Title: Main Contributions\n Main Contributions We summarize the main contributions of this paper below: • We achieve tighter upper and lower bounds on the maximal number of linear regions of the PWL function corresponding to a DNN that employs ReLUs. As a special case, we present the exact maximal number of regions when the input dimension is one. We ad- ditionally provide the first upper bound on the number of linear regions for multi-layer maxout networks (See Sections 3 and 4). • We show for ReLUs that the exact maximal number of linear regions of shallow networks is larger than that of deep networks if the input dimension exceeds the number of neurons. This result is particularly interesting, since it cannot be inferred from the bounds derived in prior work. • We use a mixed-integer linear formulation to show that exact counting of the linear regions is indeed possible. For the first time, we show the exact counting of the number of linear regions for several small-sized DNNs during the training process. This new capability can be used to evaluate the tightness of the bounds and potentially analyze the correlation between validation accuracy and the number of linear regions. It also provides new insights as to how the linear regions vary during the training process (See Section 5 and 6). 3 TIGHTER BOUNDS FOR RECTIFIER NETWORKS Montúfar et al. (2014) derive an upper bound of 2 N for N hidden units, which can be obtained by mapping linear regions to activation patterns. Raghu et al. (2017) improves this result by deriving an asymptotic upper bound of O(n Ln0 ) to the maximal number of regions, assuming n l = n for all layers l and n 0 = O(1). Montúfar (2017) further tightens the upper bound to L l=1 d l j=0 n l j , where d l = min{n 0 , n 1 , . . . , n l }. Moreover, Montúfar et al. (2014) prove a lower bound of L−1 l=1 n l /n 0 n0 n0 j=0 n L j when n ≥ n 0 , or asymptotically Ω((n/n 0 ) (L−1)n0 n n0 ). Arora et al. (2016) present a lower bound of 2 n0−1 j=0 m−1 j w L−1 where 2m = n 1 and w = n l for all l = 2, . . . , L. By choosing m and w appropriately, this lower bound is Ω(s n0 ) where s is the total size of the network. We derive both upper and lower bounds that improve upon these previous results.\n\nSection Title: AN UPPER BOUND ON THE NUMBER OF LINEAR REGIONS\n AN UPPER BOUND ON THE NUMBER OF LINEAR REGIONS In this section, we prove the following upper bound on the number of regions. Theorem 1. Consider a deep rectifier network with L layers, n l rectified linear units at each layer l, and an input of dimension n 0 . The maximal number of regions of this neural network is at most This bound is tight when L = 1. Note that this is a stronger upper bound than the one that appeared in Montúfar (2017) , which can be derived from this bound by relaxing the terms n l − j l to n l and factoring the expression. When n 0 = O(1) and all layers have the same width n, this expression has the same best known asymptotic bound O(n Ln0 ) first presented in Raghu et al. (2017) . Two insights can be extracted from the above expression: 1. Bottleneck effect. The bound is sensitive to the positioning of layers that are small relative to the others, a property we call the bottleneck effect. If we subtract a neuron from one of two layers with the same width, choosing the one closer to the input layer will lead to a larger (or equal) decrease in the bound. This occurs because each index j l is essentially limited by the widths of the current and previous layers, n 0 , n 1 , . . . , n l . In other words, smaller widths in the first few layers of the network imply a bottleneck on the bound. In particular for a 2-layer network, we show in Appendix A that if the input dimension is sufficiently large to not create its own bottleneck, then moving a neuron from the first layer to the second layer strictly decreases the bound, as it tightens a bottleneck. Figure 3a illustrates this behavior. For the solid line, we keep the total size of the network the same but shift from a small-to-large network (i.e., smaller width near the input layer and larger width near the output layer) to a large-to-small network in terms of width. We see that the bound monotonically increases as we reduce the bottleneck. If we add a layer of constant width at the end, represented by the dashed line, the bound decreases when the layers before the last become too small and create a bottleneck for the last layer. While this is a property of the upper bound rather than one of the exact maximal number of regions, we observe in Section 6 that empirical results for the number of regions of a trained network exhibit a behavior that resembles the bound as the width of the layers vary. 2. Deep vs shallow for large input dimensions. In several applications such as imaging, the input dimension can be very large. Montúfar et al. (2014) show that if the input dimension n 0 is constant, then the number of regions of deep networks is asymptotically larger than that of shallow (single-layer) networks. We complement this picture by establishing that if the input dimension is large, then shallow networks can attain more regions than deep networks. More precisely, we compare a deep network with L layers of equal width n and a shallow network with one layer of width Ln. In Appendix A, we show using Theorem 1 that if the input dimension n 0 exceeds the size of the network Ln, then the ratio between the exact maximal number of regions of the deep and of the shallow network goes to zero as L approaches infinity. We also show in Appendix A that in a 2-layer network, if the input dimension n 0 is larger than both widths n 1 and n 2 , then turning it into a shallow network with a layer of n 1 + n 2 ReLUs increases the exact maximal number of regions. Figure 3b illustrates this behavior. As we increase the number of layers while keeping the total size of the network constant, the bound plateaus at a value lower than the exact maximal number of regions for shallow networks. Moreover, the number of layers that yields the highest bound decreases as we increase the input dimension n 0 . It is important to note that this property cannot be inferred from previous upper bounds derived in prior work, since they are at least 2 N when n 0 ≥ max{n 1 , . . . , n L }, where N is the total number of neurons. We remark that asymptotically both deep and shallow networks can attain exponentially many regions when the input dimension is at least n (see Appendix B). We now build towards the proof of Theorem 1. For a given activation set S l and a matrix W with n l rows, let σ S l (W ) be the operation that zeroes out the rows of W that are inactive according to S l . This represents the effect of the ReLUs. For a region S at layer l − 1, defineW l Each region S at layer l − 1 may be partitioned by a set of hyperplanes defined by the neurons of layer l. When viewed in the input space, these hyperplanes are the rows ofW l S x + b = 0 for some b. To verify this, note that, if we recursively substitute out the hidden variables h l−1 , . . . , h 1 from the original hyperplane W l h l−1 + b l = 0 following S, the resulting weight matrix applied to x isW l S . Finally, we define the dimension of a region S at layer l − 1 as dim(S) := rank(σ S l−1 (W l−1 ) · · · σ S 1 (W 1 )). This can be interpreted as the dimension of the space corre- sponding to S that W l effectively partitions. The proof of Theorem 1 focuses on the dimension of each region S. A key observation is that once it falls to a certain value, the regions contained in S cannot recover to a higher dimension. Zaslavsky (1975) showed that the maximal number of regions in R d induced by an arrangement of m hyperplanes is at most d j=0 m j . Moreover, this value is attained if and only if the hyperplanes are in general position. The lemma below tightens this bound for a special case where the hyperplanes may not be in general position. Lemma 2. Consider m hyperplanes in R d defined by the rows of W x + b = 0. Then the number of regions induced by the hyperplanes is at most The proof is given in Appendix C. Its key idea is that it suffices to count regions within the row space of W . The next lemma brings Lemma 2 into our context. Lemma 3. The number of regions induced by the n l neurons at layer l within a certain region S is at most Proof. The hyperplanes in a region S of the input space are given by the rows ofW l S x + b = 0 for some b. By the definition ofW l S , the rank ofW l S is upper bounded by min{rank(W l ), rank(σ S l−1 (W l−1 ) · · · σ S 1 (W 1 ))} = min{rank(W l ), dim(S)}. That is, rank(W l S ) ≤ min{n l , dim(S)}. Applying Lemma 2 yields the result. In the next lemma, we show that the dimension of a region S can be bounded recursively in terms of the dimension of the region containing S and the number of activated neurons defining S. Lemma 4. Let S be a region at layer l and S be the region at layer l − 1 that contains it. Then dim(S) ≤ min{|S l |, dim(S )}. Proof. dim(S) = rank(σ S l (W l ) · · · σ S 1 (W 1 )) ≤ min{rank(σ S l (W l )), rank(σ S l−1 (W l−1 ) · · · σ S 1 (W 1 )) ≤ min{|S l |, dim(S )}. The last inequality comes from the fact that the zeroed out rows do not count towards the rank of the matrix. In the remainder of the proof of Theorem 1, we combine Lemmas 3 and 4 to construct a recurrence R(l, d) that bounds the number of regions within a given region of dimension d. Simplifying this recurrence yields the expression in Theorem 1. We formalize this idea and complete the proof of Theorem 1 in Appendix D. As a side note, Theorem 1 can be further tightened if the weight matrices are known to have small rank. The bound from Lemma 3 can be rewritten as min{rank(W l ),dim(S)} j=0 n l j if we do not relax rank(W l ) to n l in the proof. The term rank(W l ) follows through the proof of Theorem 1 and the index set J in the theorem becomes A key insight from Lemmas 3 and 4 is that the dimensions of the regions are non-increasing as we move through the layers partitioning it. In other words, if at any layer the dimension of a region becomes small, then that region will not be able to be further partitioned into a large number of regions. For instance, if the dimension of a region falls to zero, then that region will never be further partitioned. This suggests that if we want to have many regions, we need to keep dimensions high. We use this idea in the next section to construct a DNN with many regions.\n\nSection Title: THE CASE OF DIMENSION ONE\n THE CASE OF DIMENSION ONE If the input dimension n 0 is equal to 1 and n l = n for all layers l, the upper bound presented in the previous section reduces to (n + 1) L . On the other hand, the lower bound given by Montúfar et al. (2014) becomes n L−1 (n + 1). It is then natural to ask: are either of these bounds tight? The answer is that the upper bound is tight in the case of n 0 = 1, assuming there are sufficiently many neurons. Theorem 5. Consider a deep rectifier network with L layers, n l ≥ 3 rectified linear units at each layer l, and an input of dimension 1. The maximal number of regions of this neural network is exactly L l=1 (n l + 1). The expression above is a simplified form of the upper bound from Theorem 1 in the case n 0 = 1. The proof of this theorem in Appendix E has a construction with n + 1 regions that replicate them- selves as we add layers, instead of n as in Montúfar et al. (2014) . That is motivated by an insight from the previous section: in order to obtain more regions, we want the dimension of every region to be as large as possible. When n 0 = 1, we want all regions to have dimension one. This intuition leads to a new construction with one additional region that can be replicated with other strategies.\n\nSection Title: A LOWER BOUND ON THE MAXIMAL NUMBER OF LINEAR REGIONS\n A LOWER BOUND ON THE MAXIMAL NUMBER OF LINEAR REGIONS Both the lower bound from Montúfar et al. (2014) and from Arora et al. (2016) can be slightly improved, since their approaches are based on extending a 1-dimensional construction similar to the one in Section 3.2. We do both since they are not directly comparable: the former bound is in terms of the number of neurons in each layer and the latter is in terms of the total size of the network. Theorem 6. The maximal number of linear regions induced by a rectifier network with n 0 input units and L hidden layers with n l ≥ 3n 0 for all l is lower bounded by The proof of this theorem is in Appendix F. For comparison, the differences between the lower bound theorem (Theorem 5) from Montúfar et al. (2014) and the above theorem is the replacement of the condition n l ≥ n 0 by the more restrictive n l ≥ 3n 0 , and of n l /n 0 by n l /n 0 + 1. Theorem 7. For any values of m ≥ 1 and w ≥ 2, there exists a rectifier network with n 0 input units and L hidden layers of size 2m + w(L − 1) that has 2 n0−1 j=0 m−1 j (w + 1) L−1 linear regions. The proof of this theorem is in Appendix G. The differences between Theorem 2.11(i) from Arora et al. (2016) and the above theorem is the replacement of w by w + 1. They construct a 2m-width layer with many regions and use a one-dimensional construction for the remaining layers.\n\nSection Title: AN UPPER BOUND ON THE NUMBER OF LINEAR REGIONS FOR MAXOUT NETWORKS\n AN UPPER BOUND ON THE NUMBER OF LINEAR REGIONS FOR MAXOUT NETWORKS We now consider a deep neural network composed of maxout units. Given weights W l j for j = 1, . . . , k, the output of a rank-k maxout layer l is given by In terms of bounding number of regions, a major difference between the next result for maxout units and the previous one for ReLUs is that reductions in dimensionality due to inactive neurons with zeroed output become a particular case now. Nevertheless, using techniques similar to the ones from Section 3.1, the following theorem can be shown (see Appendix H for the proof). Theorem 8. Consider a deep neural network with L layers, n l rank-k maxout units at each layer l, and an input of dimension n 0 . The maximal number of regions of this neural network is at most Asymptotically, if n l = n for all l = 1, . . . , L, n ≥ n 0 , and n 0 = O(1), then the maximal number of regions is at most O((k 2 n) Ln0 ).\n\nSection Title: EXACT COUNTING OF LINEAR REGIONS\n EXACT COUNTING OF LINEAR REGIONS If the input space x ∈ R n0 is bounded by minimum and maximum values along each dimension, or else if x corresponds to a polytope more generally, then we can define a mixed-integer linear formulation mapping polyhedral regions of x to the output space y ∈ R m . The assumption that x is bounded and polyhedral is natural in most applications, where each value x i has known lower and upper bounds (e.g., the value can vary from 0 to 1 for image pixels). Among other things, we can use this formulation to count the number of linear regions. In the formulation that follows, we use continuous variables to represent the input x, which we can also denote as h 0 , the output of each neuron i in layer l as h l i , and the output y as h L+1 . To simplify the representation, we lift this formulation to a space that also contains the output of a complementary set of neurons, each of which is active when the corresponding neuron is not. Namely, for each neuron i in layer l we also have a variable h l i := max{0, −W l i h l−1 − b l i }. We use binary variables of the form z l i to denote if each neuron i in layer l is active or else if the complement of such neuron is. Finally, we assume M to be a sufficiently large constant. For a given neuron i in layer l, the following set of constraints maps the input to the output: Theorem 9. Provided that |w l i h l−1 j + b l i | ≤ M for any possible value of h l−1 , a formulation with the set of constraints (1) for each neuron of a rectifier network is such that a feasible solution with a fixed value for x yields the output y of the neural network. The proof for the statement above is given in Appendix I. More details on the procedure for exact counting are in Appendix J. In addition, we show the theory for unrestricted inputs and a mixed- integer formulation for maxout networks in Appendices K and L, respectively. These results have important consequences. First, they allow us to tap into the literature of mixed- integer representability ( Jeroslow, 1987 ) and disjunctive programming ( Balas, 1979 ) to understand what can be modeled on rectifier networks with a finite number of neurons and layers. To the best of our knowledge, that has not been discussed before. Second, they imply that we can use mixed- integer optimization solvers to analyze the (x, y) mapping of a trained neural network. For example, Cheng et al. (2017) use another mixed-integer formulation to generate adversarial examples of a DNN. That is technically feasible due to the linear proportion between the size of the neural network and that of the mixed-integer formulation. Compared to Cheng et al. (2017) , we show in Appendix I that formulation (1) can be implemented with further refinements on the value of the M constants.\n\nSection Title: EXPERIMENTS\n EXPERIMENTS We perform two different experiments for region counting using small-sized networks with ReLU activation units on the MNIST benchmark dataset ( LeCun et al., 1998 ). In the first experiment, we generate rectifier networks with 1 to 4 hidden layers having 10 neurons each, with final test error between 6 and 8%. The training was carried out for 20 epochs or training steps, and we count the number of linear regions during each training step. For those networks, we count the number of linear regions within 0 ≤ x ≤ 1 in which a single neuron is active in the output layer, hence partitioning these regions in terms of the digits that they classify. In Fig. 4 , we show how the number of regions classifying each digit progresses during training. Some digits have zero linear regions in the beginning, which explains why they begin later in the plot. The total number of such regions per training step is presented in Fig. 5(a) and error measures are found in Appendix M. Overall, we observe that the number of linear regions jumps orders of magnitude are varies more widely for each added layer. Furthermore, there is an initial jump in the number of linear regions classifying each digit that seems proportional to the number of layers. In the second experiment, we train rectifier networks with two hidden layers summing up to 22 neurons. We train a network for each width configuration under the same conditions as above, with the test error in half of them ranging from 5 to 6%. In this case, we count all linear regions within 0 ≤ x ≤ 1, hence not restricting by activation in output layer as before. The number of linear regions of these networks are plotted in Fig. 5(b), along with the upper bound from Theorem 1 and the upper bounds from Montúfar et al. (2014) and Montúfar (2017) . Error measures of both experiments can be found in Appendix M and runtimes for counting the linear regions in Appendix N.\n\nSection Title: DISCUSSION\n DISCUSSION The representational power of a DNN can be studied by observing the number of linear regions of the PWL function that the DNN represents. In this work, we improve on the upper and lower bounds on the linear regions for rectified networks derived in prior work ( Montúfar et al., 2014 ; Raghu et al., 2017 ; Montúfar, 2017 ; Arora et al., 2016 ) and introduce a first upper bound for multi-layer maxout networks. We obtain several valuable insights from our extensions. Our ReLU upper bound indicates that small widths in early layers cause a bottleneck effect on the number of regions. If we reduce the width of an early layer, the dimensions of the linear regions be- come irrecoverably smaller throughout the network and the regions will not be able to be partitioned as much. Moreover, the dimensions of the linear regions are not only driven by width, but also the number of activated ReLUs corresponding to the region. This intuition allowed us to create a 1-dimensional construction with the maximal number of regions by eliminating a zero-dimensional bottleneck. An unexpected and useful consequence of our result is that shallow networks can attain more linear regions when the input dimensions exceed the number of neurons of the DNN. In addition to achieving tighter bounds, we use a mixed-integer linear formulation that maps the input space to the output to show the exact counting of the number of linear regions for several small-sized DNNs during the training process. In the first experiment, we observed that the number of linear regions correctly classifying each digit of the MNIST benchmark increases and vary in proportion to the depth of the network during the first training epochs. In the second experiment, we count the total number of linear regions as we vary the width of two layers with a fixed number of neurons, and we experimentally validate the bottleneck effect by observing that the results follow a similar pattern to the upper bound that we show. Our current results suggest new avenues for future research. First, we believe that the study of linear regions may eventually lead to insights in how to design better DNNs in practice, for example by further validating the bottleneck effect found in this study. Other properties of the bounds may turn into actionable insights if confirmed as these bounds get sufficiently close to the actual number of regions. For example, the plots in Appendix O show that there are particular network depths that maximize our ReLU upper bound for a given input dimension and number of neurons. In a sense, the number of neurons is a proxy to the computational resources available. We also believe that analyzing the shape of the linear regions is a promising idea for future work, which could provide further insight in how to design DNNs. Another important line of research is to understand the exact relation between the number of linear regions and accuracy, which may also involve the potential for overfitting. We conjecture that the network training is not likely to generalize well if there are so many regions that each point can be singled out in a different region, in particular if regions with similar labels are unlikely to be compositionally related. Second, applying exact counting to larger networks would depend on more efficient algorithms or on using approximations instead. In any case, the exact counting at a smaller scale can assess the quality of the current bounds and possibly derive insights for tighter bounds in future work, hence leading to insights that could be scaled up.\n"}, {"role": "assistant", "content": "[Significance and novelty]\n<Improved bounds on the number of linear regions in neural networks> The paper presents improved upper and lower bounds on the maximum number of linear regions in neural networks with piecewise linear activations, building on previous works. It also discusses the exact computation of the number of linear regions in small trained networks and presents experiments during training with varying network sizes.\n<Use of linear program to compute the number of linear regions> The technique of counting the number of linear regions exactly by solving a linear program is introduced, along with experiments using this method to compute the number of linear regions on small networks during training on MNIST.\n\n[Potential reasons for acceptance]\n<Clear and well-written paper> The paper is well-written, and the reviewers appreciate the clear explanation of contributions.\n<Contribution to understanding neural networks> The work is recognized as an important step forward in understanding neural networks, particularly in terms of the theoretical aspects of deep nets.\n\n[Potential reasons for rejection]\n<Minor improvement over existing work> The improvement over existing work, especially Montufar, 2017, is considered minor, leading to concerns about the paper's significance.\n<Limited practical applicability of the proposed algorithm> The method for exact counting of linear regions using a linear program may not scale well and has limited applicability to larger networks, leading to concerns about the empirical conclusions.\n\n[Suggestions for improvement]\n<Clarification on citations and related work> Address the reviewer's concern regarding the clarification of the talk Montufar at SampTA and prioritize providing clarification on this point.\n<Detailed discussion on practicality of the proposed algorithm> Discuss in detail how practical the algorithm proposed for exact counting of linear regions is, especially in terms of its scalability to larger networks and its implications for the empirical conclusions.\n\n"}]}
- 在微调页面上传自己的数据
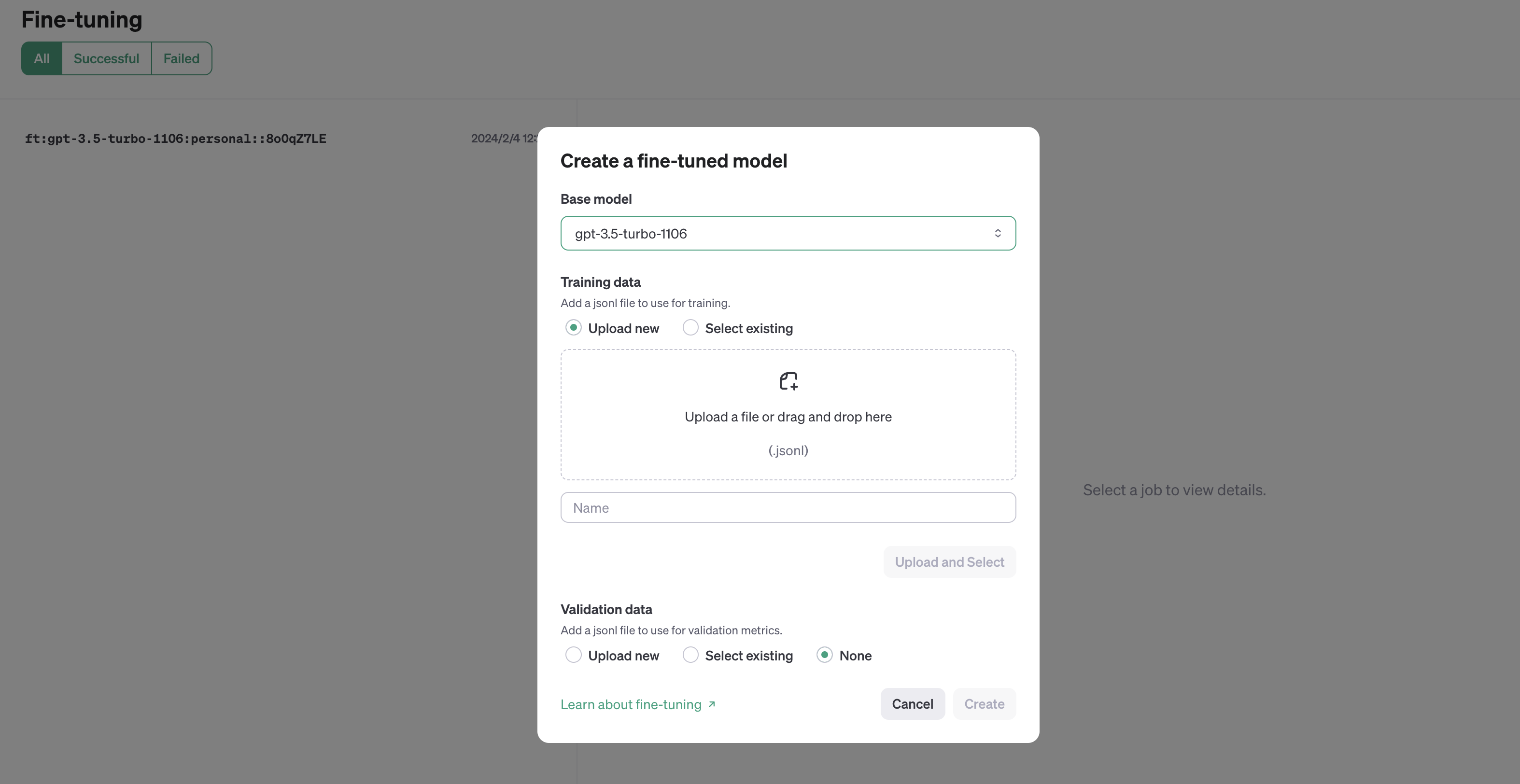
1.1.2 先后用150多条、1500多条、15000多条数据微调GPT3.5 Tubor 16K
为了先验证一下微调这个模式,故我们先用了156条paper-review数据集去微调gpt3.5 16k,然后跑完之后,我还和项目组的同事打趣说,搞不好我们是国内第一批微调gpt3.5 16k的呢,毕竟高质量的长文本数据非常稀缺
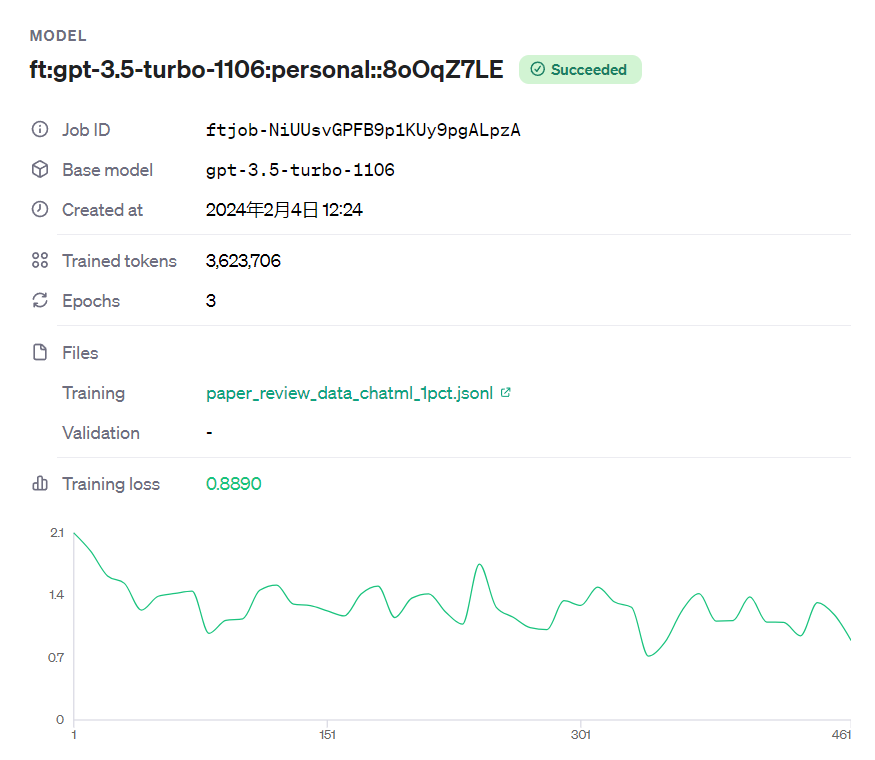
效果如何呢,我们先随机试一篇训练集之外的论文,做个验证,至于专业全面的评估下节详述
第二项目组的文弱同学用传「七月大模型线上营」群里的10pct那个数据集的倒数第二行的input(因为上面用于微调的156条数据只用了群里10%的数据,所以后面的这个input数据可以做验证集),分别让gpt3.5、微调过的gpt3.5对该input进行审稿意见的输出,且对比原始的人工审稿意见
这三个输出按顺序如下从左至右展示

1.2 对微调后的gpt3.5 16K的效果评估
// 待更
第二部分 微调13B:首选LongQLora微调Llama-2-13b-chat
在我司这个论文审稿场景下,对于13B模型的微调,首选还是微调llama 13B(模型地址:Llama-2-13b-chat-hf)
其对卡的要求:双48g的卡或者单卡80g,即13b的话双A40用longqlora差不多,所以本次微调方法继续用之前微调过llama2 7B的longqlora(当然,longlora也行,不过 考虑到尽可能节省资源,故还是longqlora了)
24年,2.3日开跑..
// 待更
参考文献与推荐阅读
- 第一阶段 开始后续第2.5版的迭代:微调GPT3.5 16K
2.3日,新增一节的内容,即
7.1.1 微调GPT3.5的前期调研:费用、微调流程等 - 2.4日,新增一节,即
7.1.2 先后用150多条、1500多条、15000多条数据微调GPT3.5 Tubor 16K
