当前位置：首页 > article >正文

代码随想录算法训练营第23天 | 669. 修剪二叉搜索树， 108.将有序数组转换为二叉搜索树，538.把二叉搜索树转换为累加树

article 2025/1/22 23:41:13

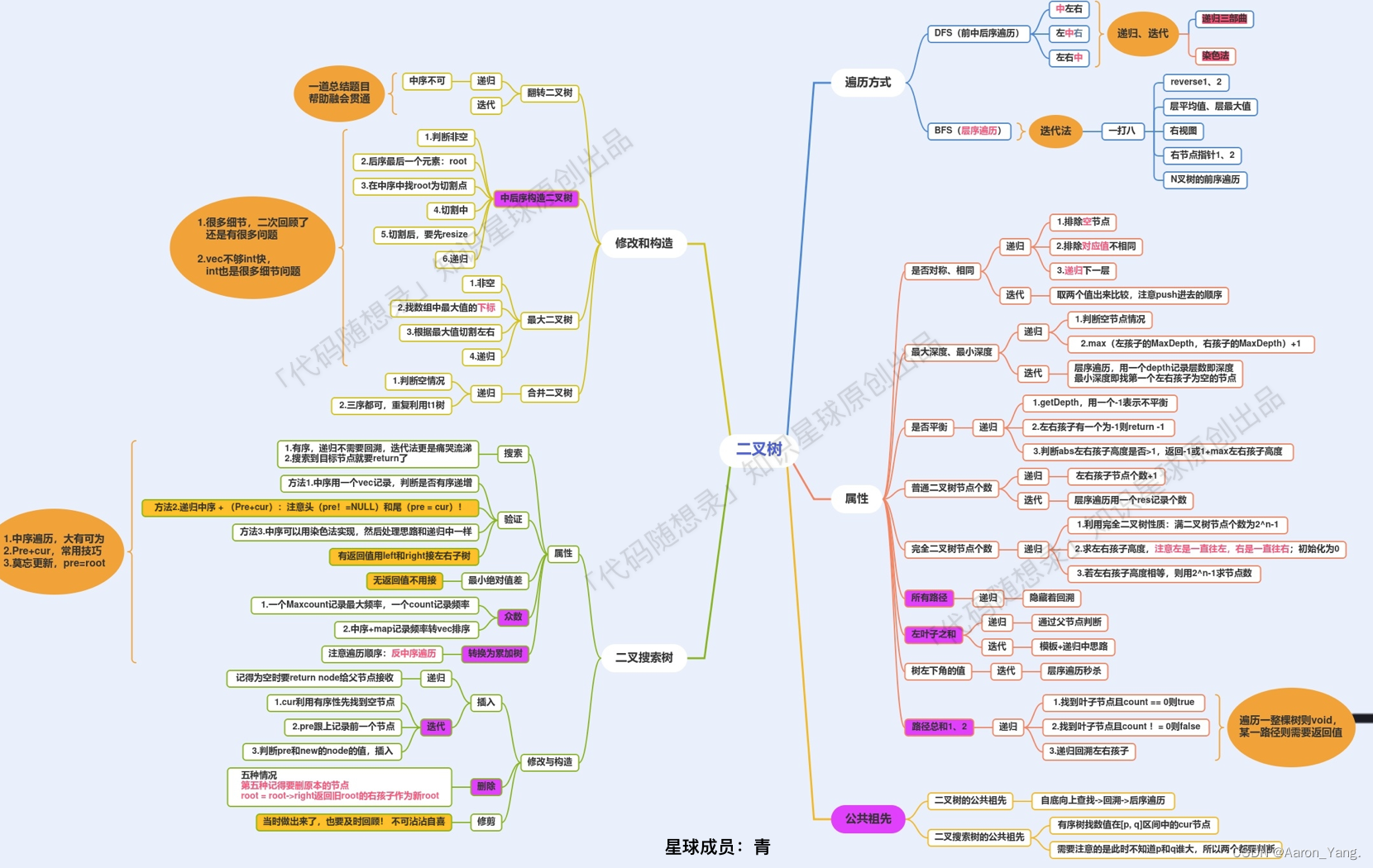
二叉树理论基础：

https://programmercarl.com/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html#%E7%AE%97%E6%B3%95%E5%85%AC%E5%BC%80%E8%AF%BE

669. 修剪二叉搜索树

题目链接：https://leetcode.cn/problems/trim-a-binary-search-tree/

思路:

最开始的想法是，递归处理，然后遇到 root->val < low || root->val > high 的时候直接return NULL，一波修改，赶紧利落。然而[1, 3]区间在二叉搜索树的中可不是单纯的节点3和左孩子节点0就决定的，还要考虑节点0的右子树。所以这个想法不可行。
但实际上不用重构那么复杂，在上图中我们发现节点0并不符合区间要求，那么将节点0的右孩子节点2 直接赋给节点3的左孩子就可以了（就是把节点0从二叉树中移除），

重点来了，单层递归的逻辑：
如果root（当前节点）的元素小于low的数值，那么应该递归右子树，并返回右子树符合条件的头结点。
如果root(当前节点)的元素大于high的，那么应该递归左子树，并返回左子树符合条件的头结点。

接下来要将下一层处理完左子树的结果赋给root->left，处理完右子树的结果赋给root->right。

最后返回root节点。

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if(root == null)    return null;
        // 修剪二叉树，如果比low还小的话，就看看root右边
        if(root.val < low) 
            return trimBST(root.right,low,high);
        // 如果比high更大，就看看root左边
        if(root.val > high)
            return trimBST(root.left,low,high);
        root.left = trimBST(root.left,low,high);
        root.right = trimBST(root.right,low,high);
        return root;
    }
}

108.将有序数组转换为二叉搜索树

题目连接：https://leetcode.cn/problems/convert-sorted-array-to-binary-search-tree/description/

思路：

题目中说要转换为一棵高度平衡二叉搜索树，注意强调是要平衡的。
根据当前数组构造一个二叉树，本质就是寻找分割点，分割点作为当前节点，然后递归左区间和右区间。
分割点很好确定，分割点就是数组中间位置的节点。如果是偶数的话，取任意一个都可以，因为题目中强调答案不是唯一的。
因为我们需要左分界点和右分界点，所以需要考虑到一个区间问题，这里我们用的是左闭右闭。然后因为要构造的话，肯定是要前序的，根节点先创建。

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
       return traversal(nums,0,nums.length-1);
    }
    // 左闭右闭 [left,right]
    public TreeNode traversal(int[] nums, int left, int right){
        if(left > right)    return null;
        int mid = (left + right) /2;
        TreeNode root = new TreeNode(nums[mid]);
        root.left = traversal(nums,left,mid-1);
        root.right = traversal(nums,mid+1,right);
        return root;

    }
}

538.把二叉搜索树转换为累加树

题目链接：https://leetcode.cn/problems/convert-bst-to-greater-tree/

思路：

一开始不理解他题目意思，其实这个题意思很简单。就是一个二叉搜索树，把树中比他当前节点大的值都加上，然后返回一个新的二叉树即可。
这样的话，我们只需要从右子树开始遍历即可，因为右子树是最大的，从大到小我们依次累加起来，即可。因为小的数是所有值都能加的，而大的数不行。因此，这道题的递归顺序也就出来了，是后中左，代码也就很好写了。
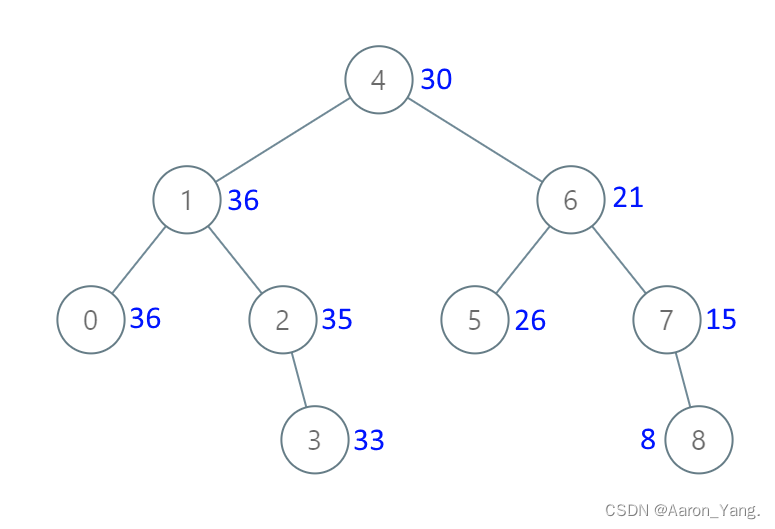
在这里插入图片描述

class Solution {
    int sum = 0;
    public TreeNode convertBST(TreeNode root) {
        // 题目意思就是让比他大的值都加起来
        if(root == null)    return root;
        // 右中左  根据搜索二叉树的特性
        root.right = convertBST(root.right);
        sum += root.val;
        root.val = sum;
        root.left = convertBST(root.left);
        return root;
    }
}