Java栈和队列
🐵本文章将对栈相关知识进行讲解

一、什么是栈
栈是一种特殊的线性表,向栈中放入元素的次序是由栈底到栈顶依次放入,被称为入栈或压栈,从栈中出元素时只能从栈顶出,被称为出栈。即栈要求元素“先进后出”

下面给一道经典的例题:
1. 若进栈序列为 1,2,3,4 ,进栈过程中可以出栈,则下列不可能的一个出栈序列是()
A: 1,4,3,2 B: 2,3,4,1 C: 3,1,4,2 D: 3,4,2,1
答案:C ;1,2,3依次入栈,之后3出栈后只能让2出栈后才能让1出栈
二、Stack类
Stack是Java提供的类,其中包含了可以对栈进行一系列操作的常见方法

栈的常用方法如下:
E push(E e) //将e入栈,并返回e
E pop() //将栈顶元素出栈并返回
E peek() //获取栈顶元素,栈顶元素不出栈
int size() //获取栈中有效元素个数
boolean empty() //检测栈是否为空
三、模拟实现栈
有两种实现栈的方法,一是用数组,二是用链表
在Stack类中方法的底层就是用的数组实现的,所以这里也用数组来模拟实现栈
public class MyStack {
public int[] elem;
public int usedSize; //记录栈中存放元素的个数
public static final int DEFAULT_CAPACITY = 5; //栈的默认容量
public MyStack() {
this.elem = new int[DEFAULT_CAPACITY];
}
/*实现栈中的方法*/
...
}public void push(int val)元素入栈,也就是在数组的usedSize位置放入元素,入栈后usedSize++;和顺序表一样也要考虑数组是否已经满了,如果满了则要扩容
public void push(int val) {
if (isFull()) {
elem = Arrays.copyOf(elem, elem.length * 2);
}
elem[usedSize++] = val;
}
public boolean isFull() { //判断数组是否满了的方法
return usedSize == elem.length;
}
public int pop()将栈顶元素出栈并返回,当然如果栈为空的话则要抛出异常
public int pop() {
if (empty()) {
throw new EmptyStackException("栈为空");
}
usedSize--;
return elem[usedSize];
}
public boolean empty() { //判断栈是否为空的方法
return usedSize == 0;
}
public int peek()只获取栈顶元素,不出栈
public int peek() {
if (isEmpty()) {
throw new EmptyStackException("栈为空");
}
int val = elem[--usedSize]; //获取栈顶元素
usedSize++; //由于元素不出栈,所以要usedSize++
return val;
}
用链表实现栈,如果用单链表的话,由于入栈操作要保证时间复杂度为O(1),所以必须用头插法,同理,出栈操作必须用头删法;但对于双向链表来说,由于其有指向最后一个节点的引用last和指向前驱节点的引用prev,所以更加灵活,入栈操作可以头插也可以尾插,出栈操作可以头删也可以尾删
在LinkedList类中有实现栈中的方法
四、相关概念
栈、虚拟机栈、函数栈帧;这里对这几个概念进行一个浅浅的区分
栈是一种数据结构
虚拟机栈是JVM的一块内存
函数栈帧是调用方法时为方法开辟的一块内存
五、什么是队列
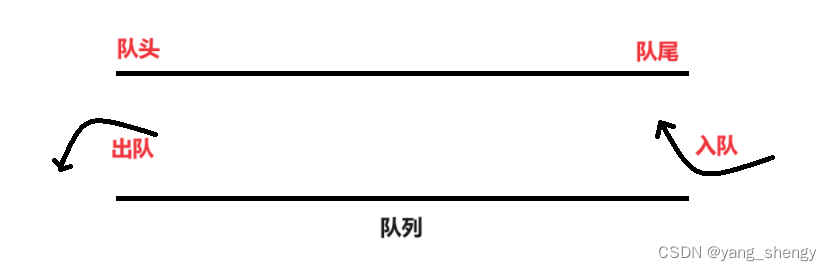
队列也是一种特殊的线性表,元素只能从队列的队尾进入,被称为入队,从队列中出元素时只能从队头出,被称为出队。即队列要求元素“先进先出”
六、Queue接口
Queue是Java提供的接口,其中包含了对队列进行一系列操作的常见方法

由于Queue是一个接口,在实例化时必须实例化LinkedList对象,因为LinkedList实现了Queue接口
在Queue接口中有以下几个方法:
boolean add(E e);
boolean offer(E e); //入队
E remove();
E poll(); //出队
E element();
E peek(); //获取队头元素
下面分别讨论一下1.add和offer的区别 2.remove 和 poll的区别 3.element 和 peek的区别
1.add 和 offer
这两个方法都是将一个元素插入到一个队列的队尾,也就是入队,区别在于:对于一个有限队列,在队列容量满的情况下,add方法会抛出IllegalStateException的异常,而offer方法则会返回false
2.remove 和 poll
这两个方法都是将队头元素删除并返回,也就是出队,区别在于:对于一个空队列,remove方法会抛出异常,poll方法会返回null
3.element 和 peek
这两个方法都是获取队头元素,区别在于:对于一个空队列,element方法会抛出异常,peek方法会返回null
对于队列进行操作的常用的方法如下:
boolean offer(E e) //入队列
E poll() //出队列
E peek() //获取队头元素
int size() //获取队列中有效元素个数
boolean isEmpty() //检测队列是否为空
七、模拟实现队列
Queue接口中的方法在底层是用链表实现的,这里我们使用双链表模拟实现队列,创建一个MyQueue类:
public class MyQueue {
static class ListNode{
public int val;
public ListNode next;
public ListNode prev;
public ListNode(int val) {
this.val = val;
}
}
public ListNode head;
public ListNode last;
/*以下为要模拟实现的方法*/
...
}boolean offer(E e)元素只能从队尾入队,对于双链表,入队操作可以看作头插也可以看作尾插,这里使用尾插法实现offer方法
public void offer(int val) {
ListNode node = new ListNode(val);
if (head == null) {
head = last = node;
} else {
last.next = node;
node.prev = last;
last = node;
}
}boolean poll()元素只能从队头出队,对于双链表,出队操作可以看作头删也可以看作尾删,由于前面入队采取的是尾插,所以这里采用头删法入队
当队列为空时,返回-1(这里假定队列中的元素都是int型);然后进行正常的头删
public int poll() {
if (head == null) {
return -1;
}
int val = head.val;
head.next.prev = null;
head = head.next;
return val;
}
这里有一种特殊的情况要考虑,就是链表中只有一个节点时上述代码会抛出空指针异常,所以这种情况要单独处理,完整代码如下:
public int poll() {
if (head == null) {
return -1;
}
int val = head.val;
if (head.next == null) {
head = last = null;
return val;
}
head.next.prev = null;
head = head.next;
return val;
}
E peek()获取队头元素,只需要将head.val 返回即可
public int peek() {
if (head == null) {
return -1;
}
return head.val;
}八、循环队列
8.1 为什么要有循环队列
对于一个数组,如下:

为了减小空间的浪费,于是就有了循环队列
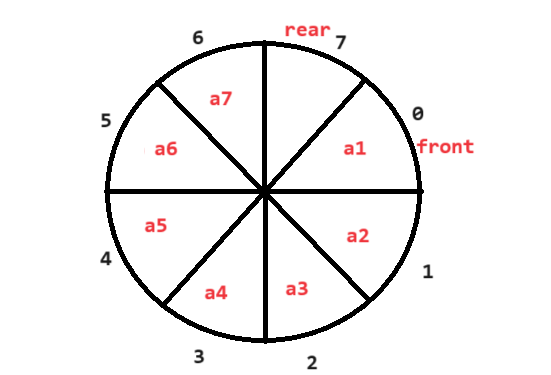
8.2 什么是循环队列
循环队列又称为环形队列,循环队列中已出队的元素的位置可以作为入队元素的位置,减小了空间的浪费

由上图可以看出循环队列是一个有限队列,那么该如何判断队列是否为满的,这里介绍三种方法:
1.计数器:定义一个count,每入队或出队一个元素都进行计数,当count等于队列的长度时说明队列已满
2.使用标记
3.空出一个位置:空出的位置不放元素,当(rear + 1) % elem.length == front 时说明队列已满
8.3 模拟实现循环队列
这里用数组实现循环队列
public class MyCircularQueue {
public int[] elem;
public int front; //队头
public int rear; //队尾
public MyCircularQueue(int k) {
elem = new int[k];
}
/*以下是要模拟实现的方法*/
...
}boolean enQueue(int value) //入队首先判断一下队列是否已满,如果为满则直接返回false,这里使用上述讲过的第三种方法来判断队列是否已满,rear指向队尾元素的下一个位置,在队尾插入元素只需要elem[rear] = value即可,插入元素后要将rear指向队尾元素的下一个位置,这里不能简单的让rear = rear + 1;因为当rear = elem.length时如果让rear + 1就会导致数组越界

public boolean enQueue(int value) {
if (isFull()) {
return false;
}
elem[rear] = value;
rear = (rear + 1) % elem.length;
return true;
}
public boolean isFull() {
return (rear + 1) % elem.length == front;
}
boolean deQueue() //出队对于数组来说,出队操作只需让front指向其下一个位置即可,这里同样不能让front = front + 1,而是front = (front + 1) % elem.length
public boolean deQueue() {
if (isEmpty()) {
return false;
}
front = (front + 1) % elem.length;
return true;
}
public boolean isEmpty() {
return rear == front;
}
int Front() //获取队头元素 public int Front() {
if (isEmpty()) {
return -1;
}
return elem[front];
}
int Rear() //获取队尾元素由于指向队尾元素的下一个位置,所以队尾元素应该是elem[rear - 1],但是当rear为0时就变成了elem[-1],无法获取队尾元素,所以分为两种情况:int index = rear == 0 ? elem.length - 1 : rear - 1
public int Rear() {
if (isEmpty()) {
return -1;
}
int index = (rear == 0) ? elem.length : rear - 1;
return elem[index];
}
🙉本篇文章到此结束,接下来会对二叉树相关知识进行讲解
