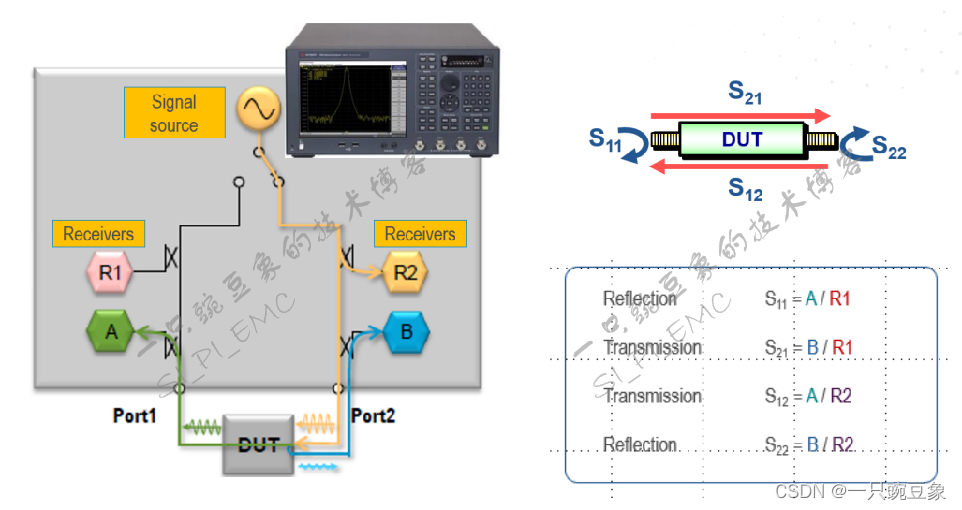
如何正确理解和获取S参数

S参数是网络参数,定义了反射波和入射波之间的关系,给定频率的S参数矩阵指定端口反射波b的矢量相对于端口入射波a的矢量,如下所示:
b=S∙a
在此基础上,如下图所示,为一个常见的双端口网络拓扑图:
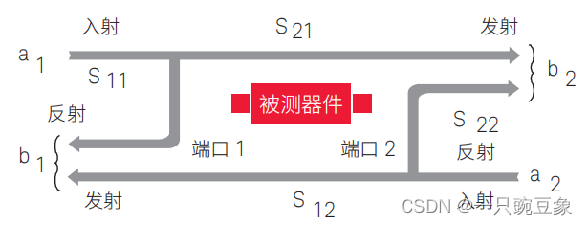
其S参数矩阵就可以表示如下:
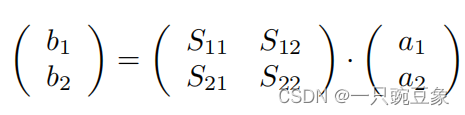
上图中矩阵下标的命名规则,可由下图进行定义描述:假设DUT为一段传输线,当传输线阻抗与端口阻抗不匹配时,会发生信号反射,一部分入射波能量会反射回输入端口,反射波和入射波的能量比值,称之为S11(回波损耗),另一部分入射波能量会沿着传输线继续向输出端传播,那么到达输出端的入射波与初始注入输入端的入射波的能量比值,称之为S21(插入损耗),当输入和输出端口发生互换时,即可得到S22和S12。
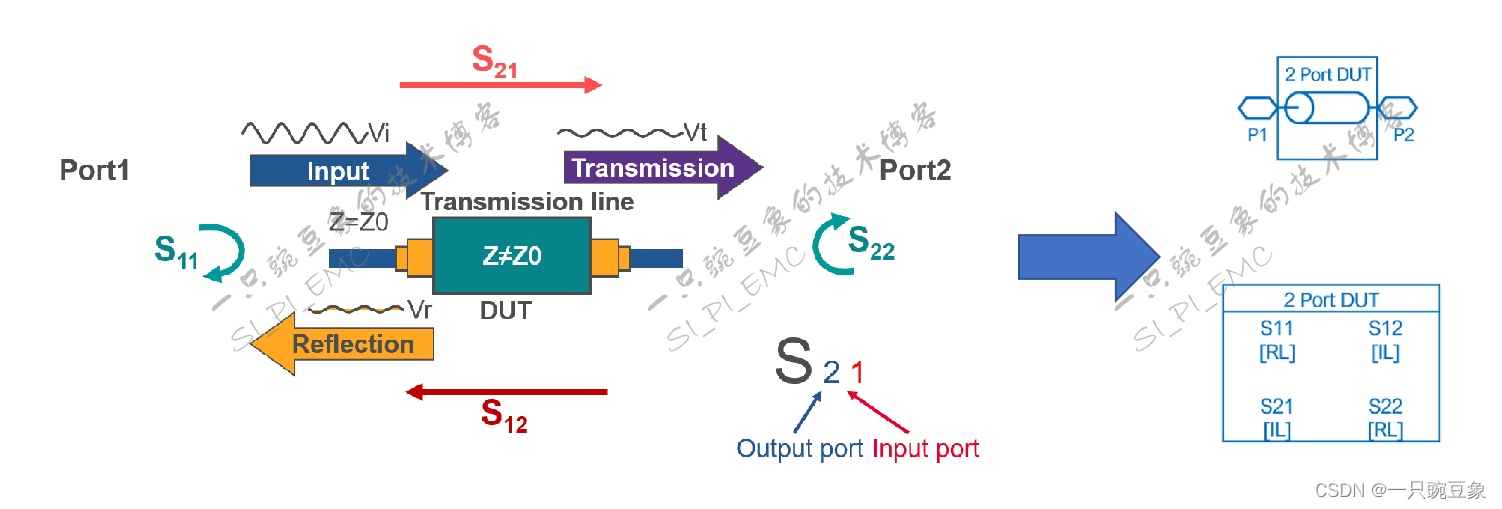
当双端口网络演变为普通的四端口网络时,两个独立运行的传输线之间,必然会由于分布参数的影响(图中的Cm和Lm)产生能量耦合效应,从而形成线间的串扰,并且,根据串扰传播的不同方向,会形成远端串扰(FEXT)和近端串扰(NEXT)的定义,那么,S参数会在双端口矩阵的基础之上,增加了端口到端口之间的能量串扰的定义描述。

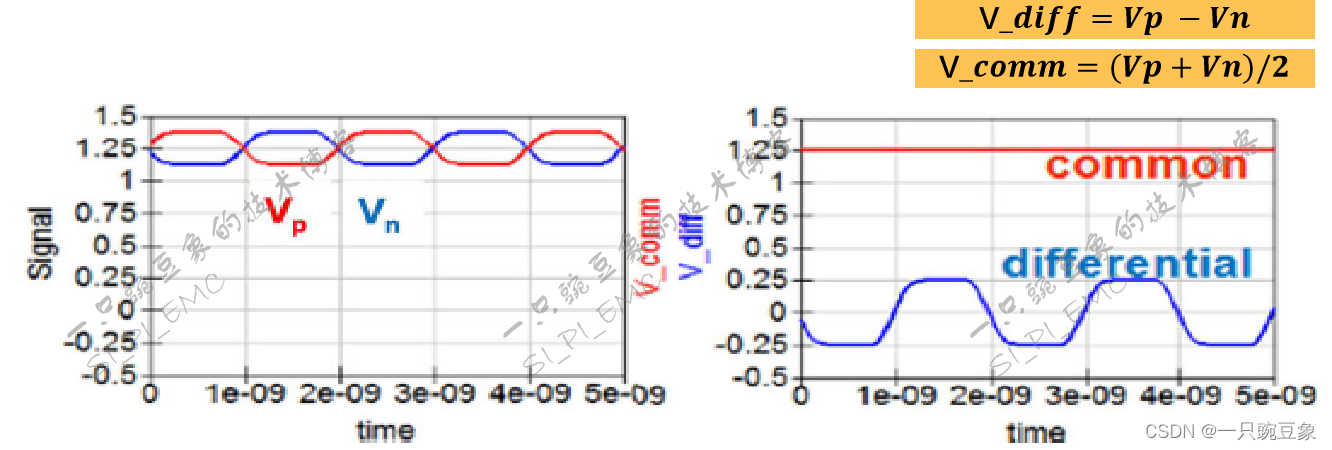
众所周知,为了实现更高速率的信号传输,差分传输系统会将有用信号叠加在一个直流偏置电压之上进行长距离的传输,以此达到将低电平变化的有用信号与地噪声之间进行隔离的效果,这种方式虽然有效,但导致了传输系统中存在两种能量分量:差模(Differential mode)和共模(Common mode),其定义如图所示的,对于工作而言,共模能量不是必须的,因此在终端,通常会使用隔直电容进行滤除,但如果“滤波”效果不理想时,共模能量还是会与差模能量一起流入到端口中,并且由于两种能量均来自于有用信号,进而导致了两种能量之间的转换。
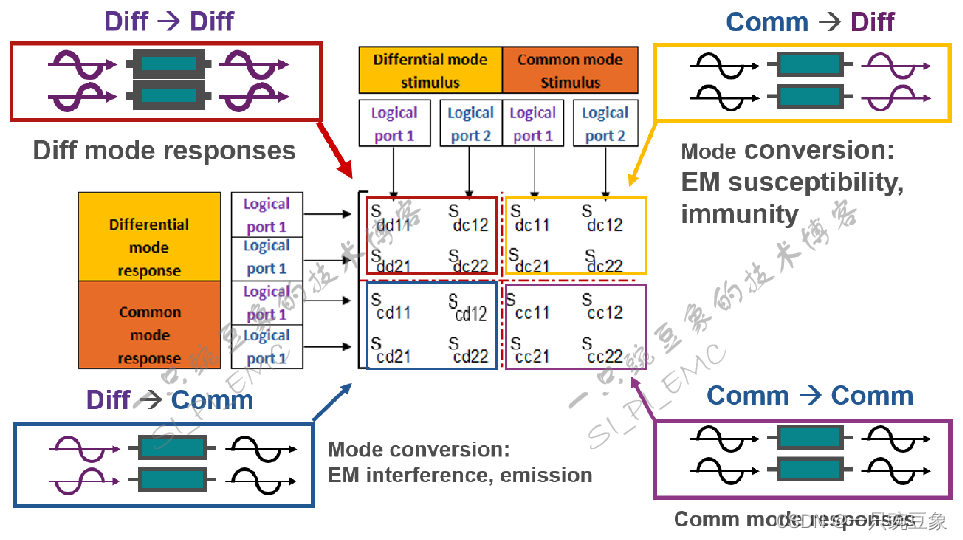
当把这种转换定义到S参数的端口矩阵中时,会形成如下的混合模式S参数矩阵,拓扑图看起来虽然略显复杂,但可以将其理解为是普通四端口网络的“强化版”:左上和右下分别是独立的差模和共模系统,左下和右上的串扰部分则被模式能量转换所替代。
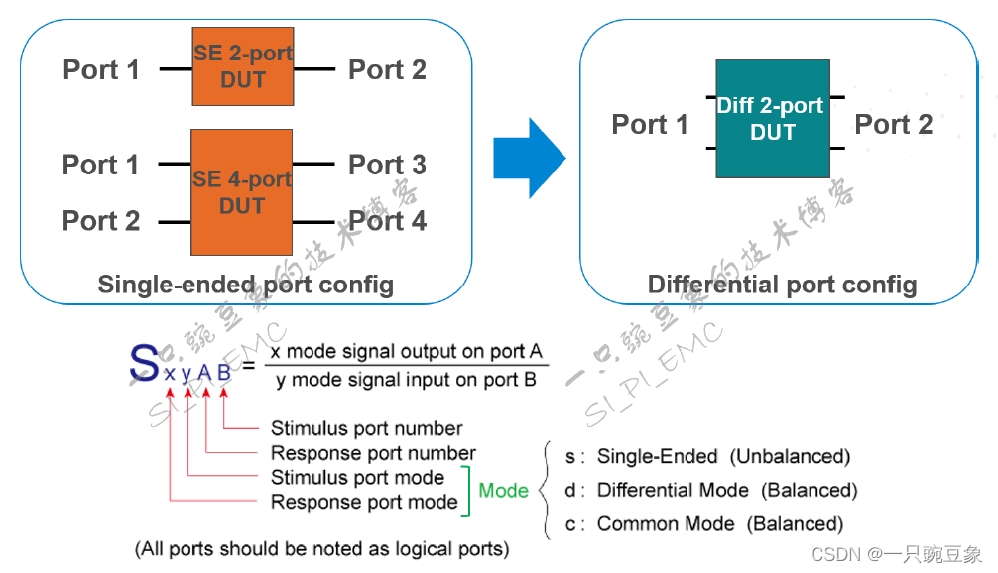
差分系统的矩阵下标的具体定义如下图所示,需要注意的,是其中s和d的区别:当DUT系统的port 1和port 2之间满足互易性(即结构对称)时,称之为差分平衡模式--d;当不满足互易性(即结构非对称)时,称之为单端非平衡模式--s,即s就可以表征差分结构中的不对称现象。
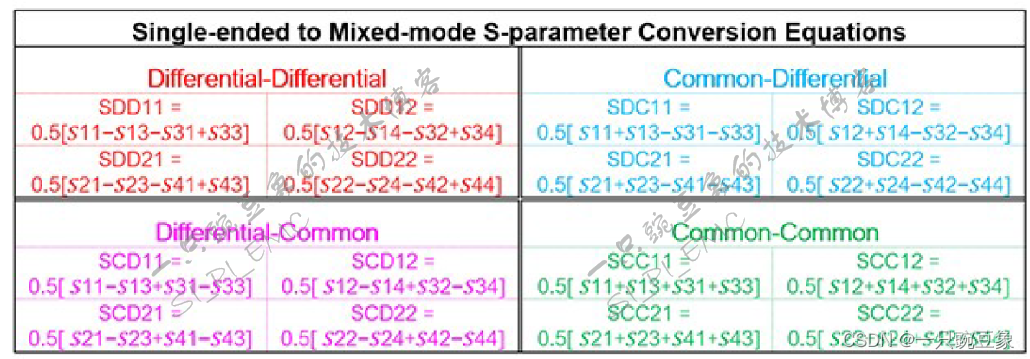
如上所述,因为差分四端口的S参数是由双端口S参数逐步演化而来,因此,在数学中,其各分量均可以从单端S参数推导而来,其具体关系如下图的公式矩阵所示,在实际的仿真和测试中,软件和测量设备也是通过获取单端S参数矩阵再进行运算得到混合S参数矩阵的,并非直接获取。
以一个简单的仿真举例说明上述公式的应用,对一段3米的USB线缆提取S参数,有以下两种方式:
方式1,直接提取单端四端口的S参数,再以上述计算公式的方式获取混合模式S参数;
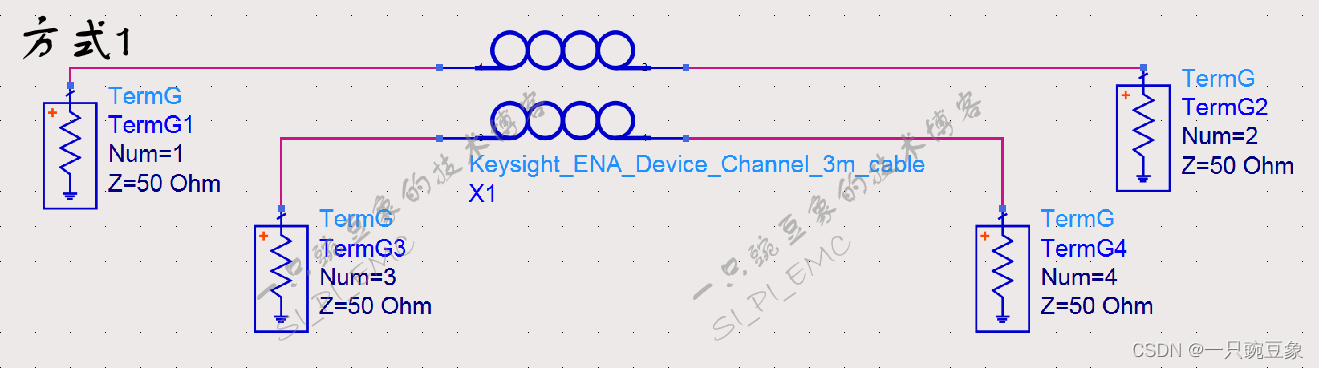
方式2,利用仿真软件中自带的模式转换器(Balun4Port),自动获取混合模式S参数。

其中,方式1在进行S参数计算时,一定要分清楚各个单端端口的摆放顺序,并分别获取如下的四组参数的计算公式:

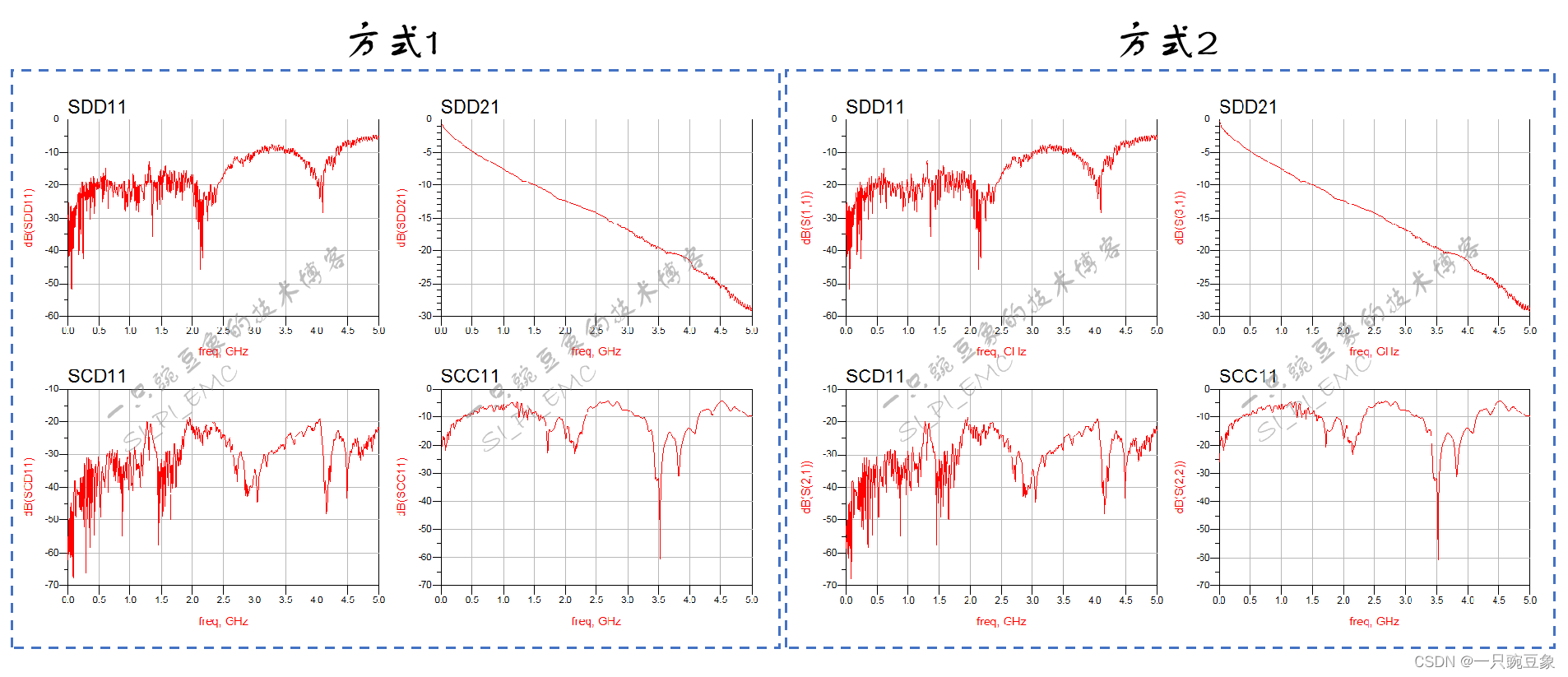
最后的结果显示,两种方式提取的混合S参数结果,几乎一模一样,并看不出明显的差异,从而说明了公式提取的准确性。
有了上述关于S参数的系统概念,再返回来查看网络分析仪的工作原理,即便描述非常简单,相信你的理解也将更为深刻!!!