深度学习入门笔记(八)可以不断思考的模型:RNN与LSTM
8.1 循环神经网络RNN
之前学到的 CNN 和全连接,模型的输入数据之间是没有关联的,比如图像分类,每次输入的图片与图片之间就没有任何关系,上一张图片的内容不会影响到下一张图片的结果。但在自然语言处理领域,这就成了一个短板。
RNN因此出现,它是一类用于处理序列数据的神经网络。其基本单元结构如下
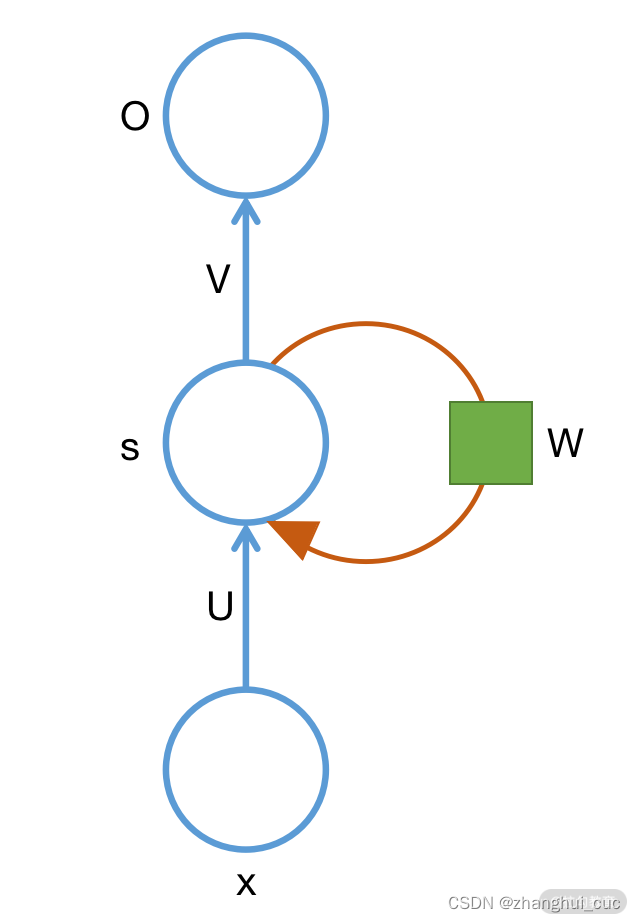
自底向上的三个蓝色的节点分别是输入层、隐藏层和输出层。U 和 V 分别是连接两个层的权重矩阵。如果不考虑右边的棕色环路的话,就是一个典型的全连接的网络。
将上面的环路展开,如下
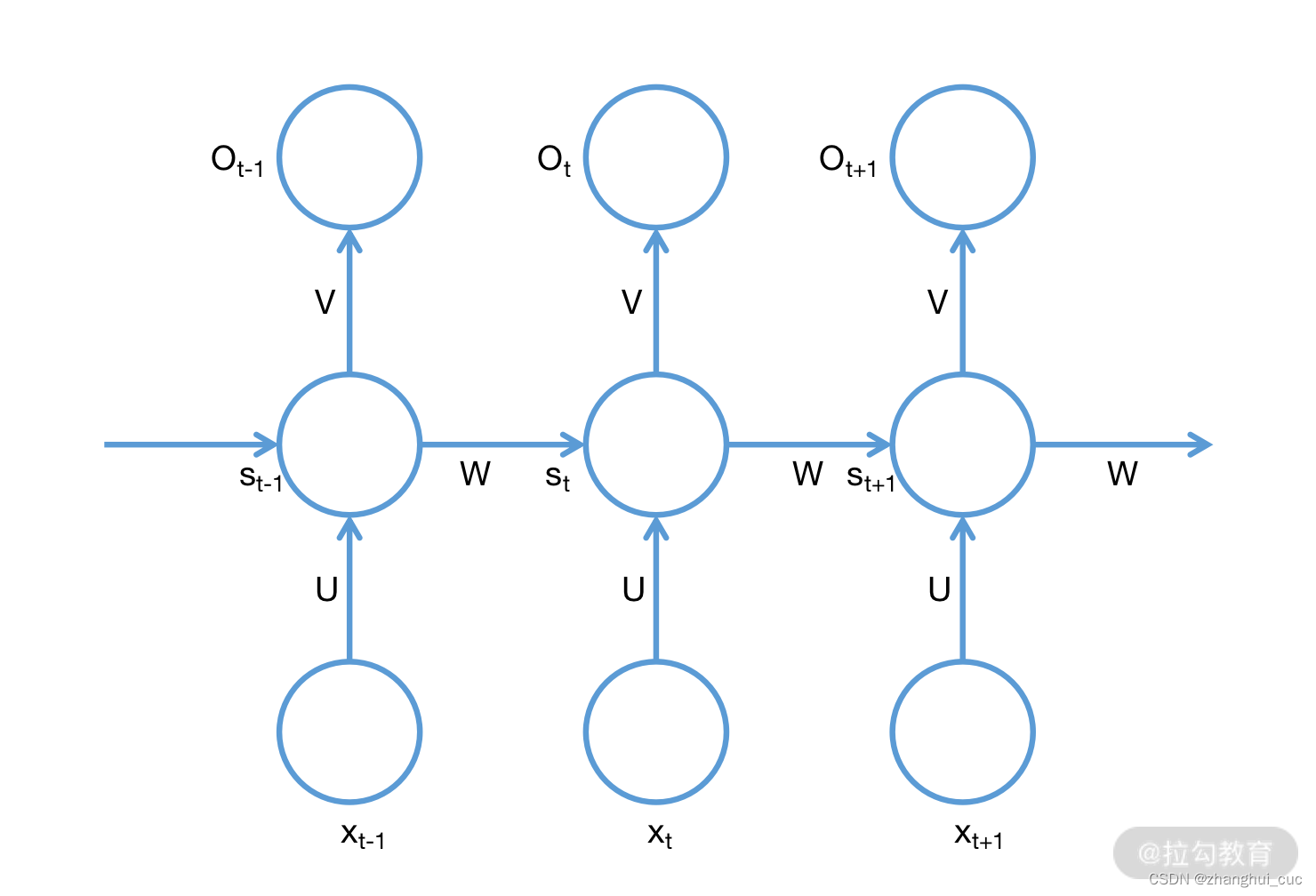
含义为:在 t 时刻,网络接受输入 Xt 和来自 t-1 时刻的隐藏层状态 St-1,并产生一个 t 时刻的隐藏层状态 St,以及 t 时刻的输出 Ot。其公式化的表示为:
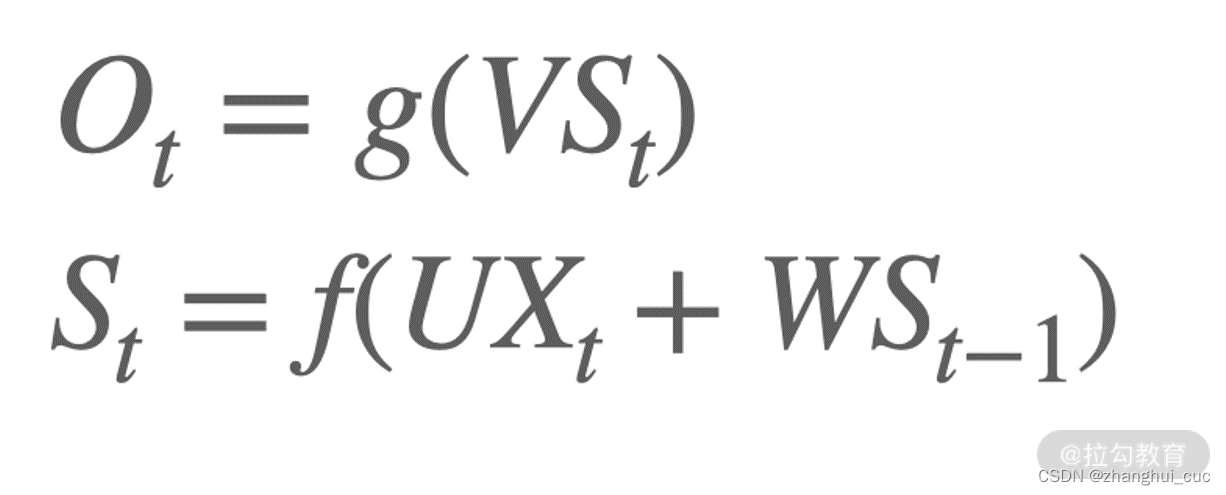
其中 g 和 f 是各自节点的激活函数。这里面需要注意的一点是,对于每一个时间 t,U、V、W 都是同一个,这非常类似上一章讲到的权值共享。
RNN 的权值共享主要出于两方面的考虑:
- 减少参数量,也减少计算量
- RNN 接受的输入是可变长的,如果不进行权值共享,那每个 W 都不同,我们无法提前预知需要多少个 W,实现上的计算就会非常困难。
以上是典型的RNN结构。
8.1.1 变体:双向RNN(BiRNN)
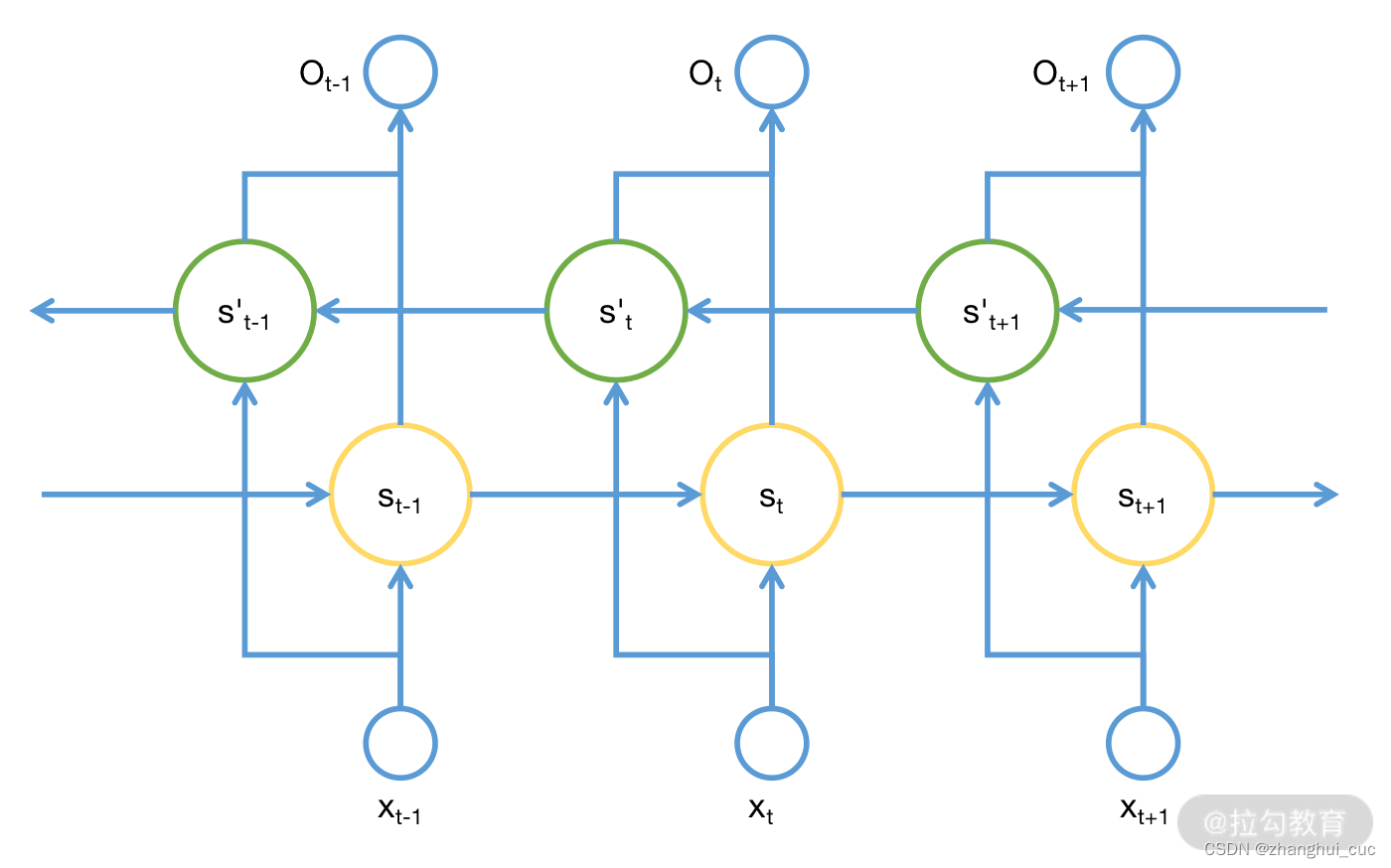
相比于 RNN,BiRNN 维持了两个方向的状态。正向计算和反向计算不共享权重,也就是说 U、V、W 分别有两个,以对应不同的方向。其公式化的表示就变成了如下的形式:
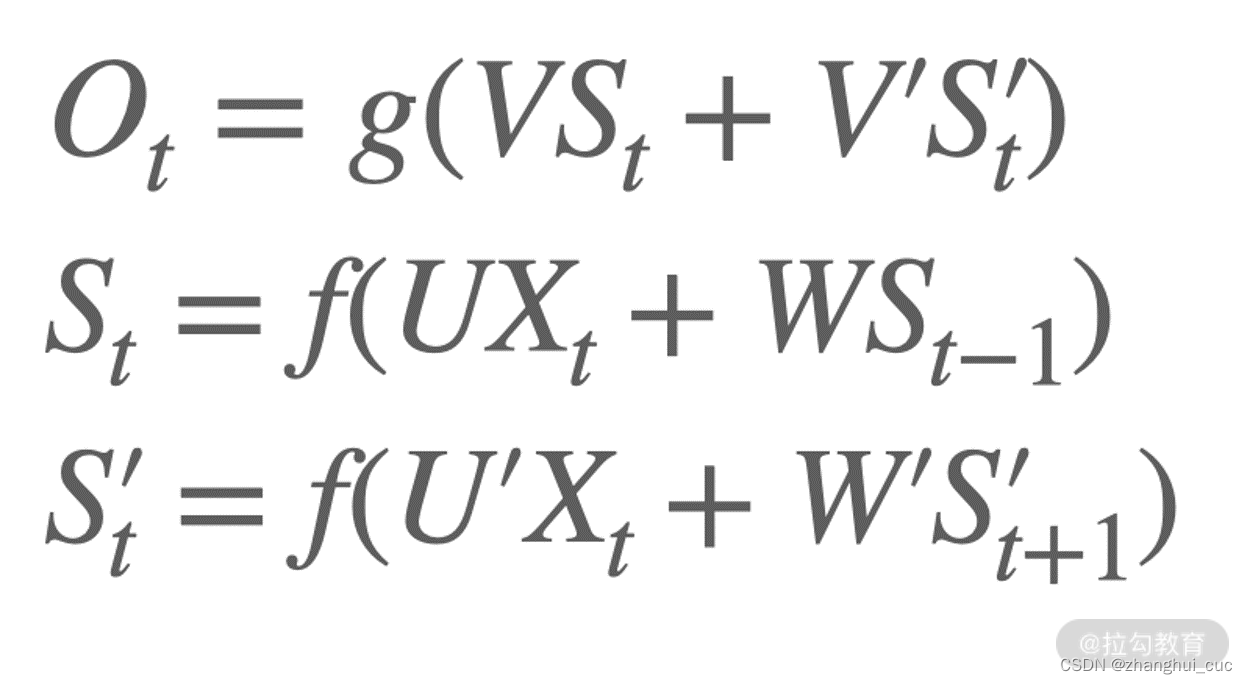
8.1.2 变体:深度RNN
前面介绍的结构中,隐藏层只有一层,但在实际的使用中,也经常会增加隐藏层的数量,即为深度RNN,能够捕获和关联更多的前后信息以提升效果。
8.2 RNN 的梯度消失与爆炸
我们尝试求 RNN 的梯度,首先明确函数关系,如下所示:
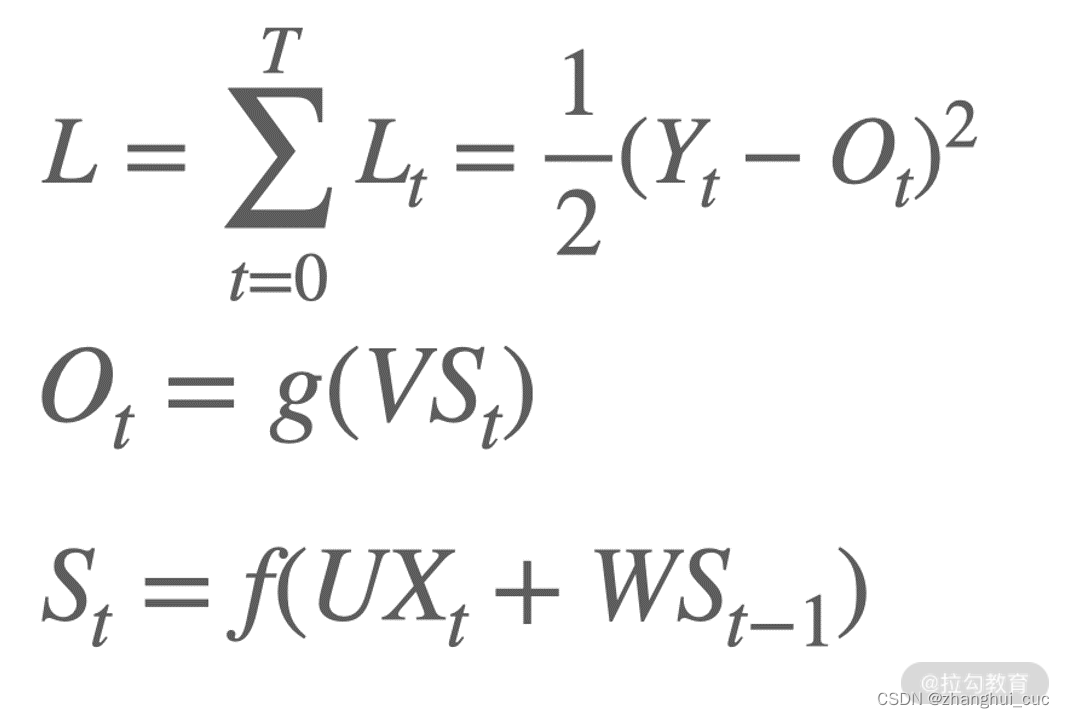
求梯度实际上是求 W、V、U 的偏导数。我们以 L 对 W 在 t 时刻求偏导数为例,推导过程如下:
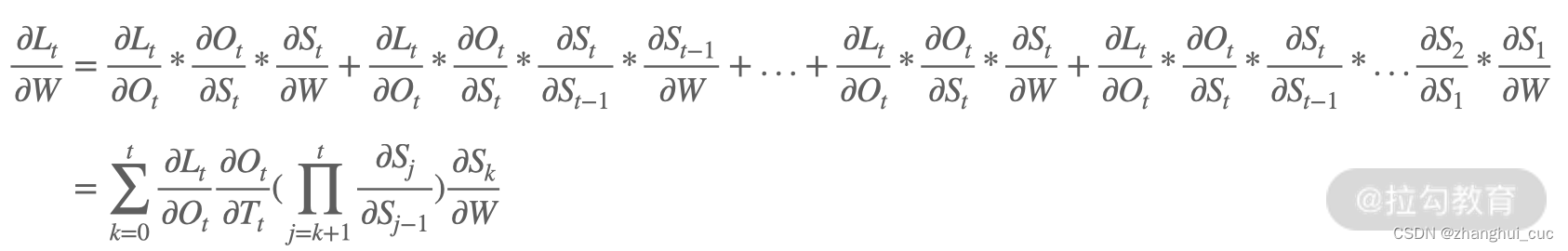
可以发现,L 关于 W 的偏导数会随着序列的长度而产生长期依赖。
也就是指当前系统的状态,可能受很长时间之前系统状态的影响,这是RNN中无法解决的一个问题。
而且RNN 一般会使用 tanh 函数作为它的激活函数,而 tanh 的导数在 0-1 之间。如此一来,如果 W 也是在 0-1之间,随着 t 的增大,梯度计算中连续相乘就会变得很长,很多个在 0~1 之间的数相乘会逐渐接近 0。梯度接近 0 则意味着梯度消失了;反之如果 W 很大,则梯度也会变得非常大,进而产生梯度爆炸,这是一个很严重的问题。
这就是接下来要介绍的长短期记忆网络要解决的问题。
8.3 长短期记忆网络LSTM
针对RNN的问题,如果我们能让 RNN 在接受上一时刻的状态和当前时刻的输入时,有选择地记忆和删除一部分内容(或者说信息),问题就可以解决了,比如有一句话提及刚才吃了苹果,那么在此之前说的吃香蕉的内容就没那么重要,删除就好了。
LSTM结构如下
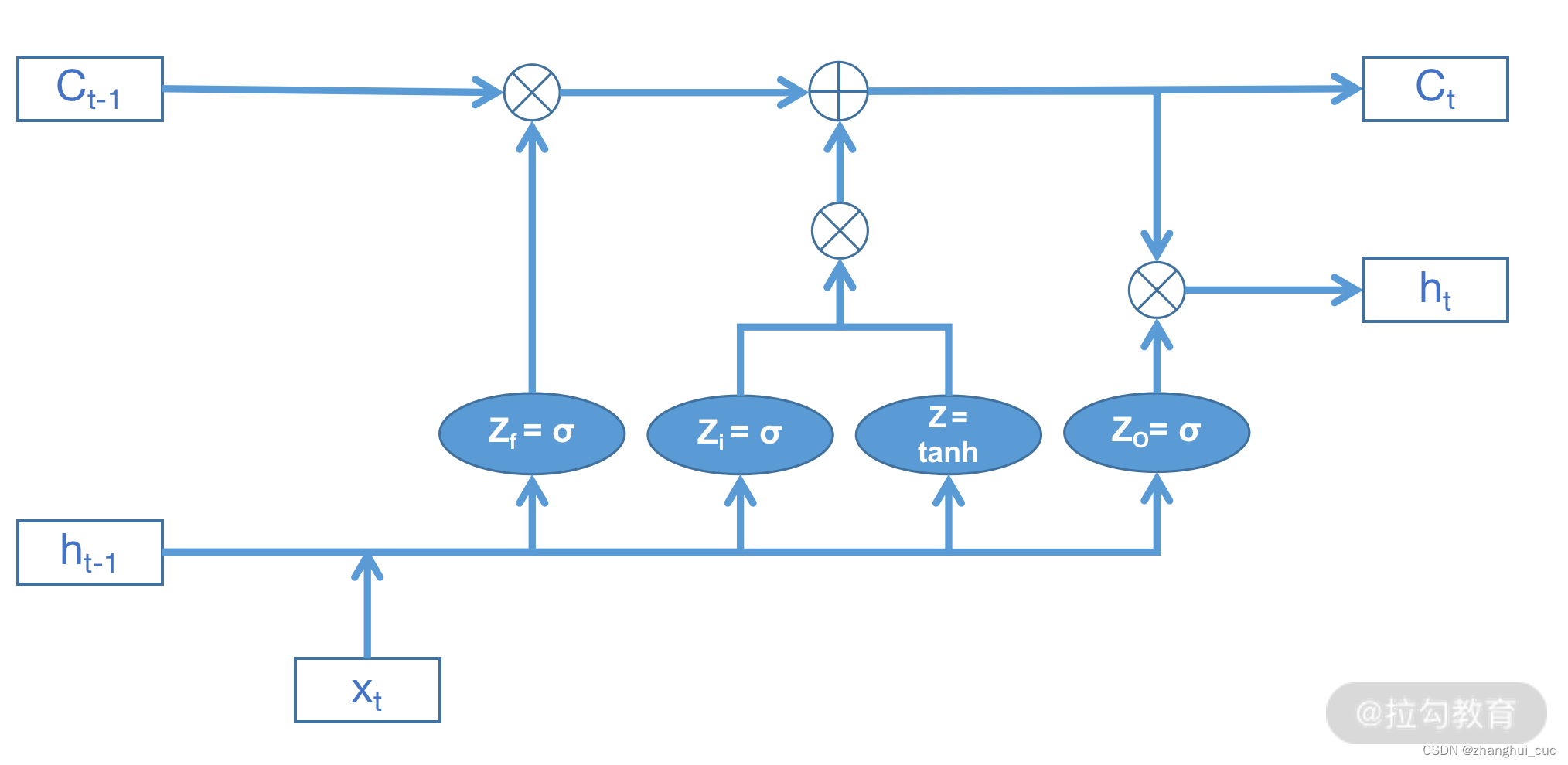
Ct-1表示上一时刻的细胞状态(cell state),ht-1则表示上一时刻的隐藏状态(hidden state)。
LSTM 独特的地方在于它内部使用了 3 个逻辑门来控制细胞的状态,分别是遗忘门、输入门和输出门,并对应了忘记、选择、更新、输出这 4 个不同的阶段,从而有选择性地保留或删除信息。
忘记阶段
刚才说过,对于上一时刻的状态我们如果能够选择性地记忆就好了。LSTM 中就使用了 Zf这个逻辑门来实现相应的功能,这个逻辑门实际上是一个 Sigmoid 单元,我们称为遗忘门。Sigmoid 可以将输入映射在 0~1 之间,得到的值再与 Ct-1相乘,这样就实现了对上一时刻状态 Ct-1的控制,即哪些信息保留或者删除多少。遗忘门的公式化表示为:
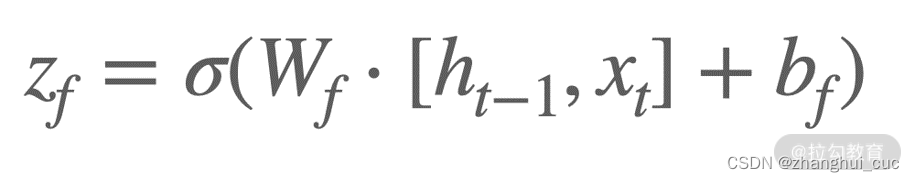
选择阶段
忘记阶段用来选择性保留或者删除上一时刻的内容,选择阶段决定给当前时刻的细胞状态添加哪些新的信息。
这个阶段包括 2 个环节:首先是利用 ht-1和 xt通过 1 个 Sigmoid 单元决定更新哪些信息,然后利用 ht-1和 xt通过 1 个 tanh 层得到新的候选细胞信息,这些信息会根据计算的结果更新到细胞中。这个过程就是输入门,公式化表示为:
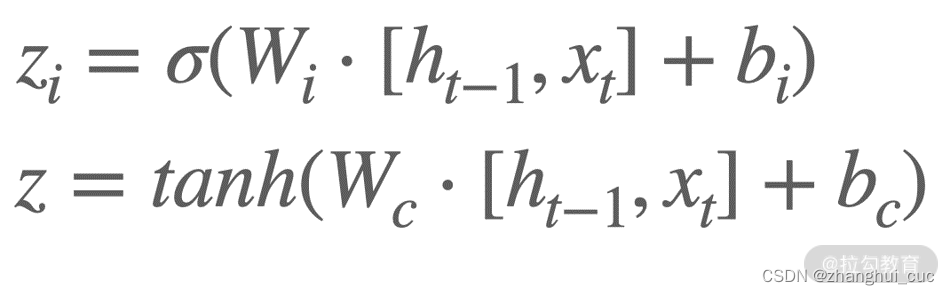
更新阶段
接下来就要对细胞状态 C 进行更新了。这个环节实际上就是把前 2 个环节得到的结果与对应的信息相乘后再加起来,其公式化表示如下:
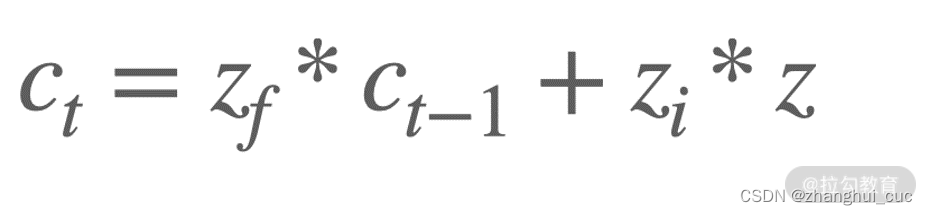
zf 和 zi 分别控制了上个阶段和当前阶段要保留多少内容,ct-1 和 zi 则是上个阶段和当前阶段的内容本身。
输出阶段
更新完细胞的状态,就到了最终的输出环节。ht-1 和 xt 这 2 个信息经过一个叫输出门的 Sigmoid 逻辑单元后,与经过 tanh 后被缩放到-1~1 之间的细胞状态 Ct 信息相乘,就得到了当前时刻的隐藏状态 ht。得到 ht 之后,就能得到当前时刻的输出 y 了。ht 的计算过程如下:
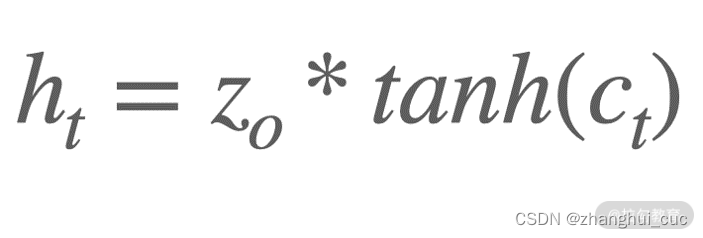
LSTM依然有明显缺点:
- 并行化困难:LSTM 的本质是一个递归的训练过程,随着实际问题的愈发复杂,这个缺点就会越来越致命。
- 梯度消失。LSTM 虽然在一定程度上缓解了 RNN 的问题,但是对于长序列的情况,仍有可能会出现梯度消失。
- LSTM 在计算的时候需要的资源较多。
所以在NLP领域,LSTM逐渐被现在大热的Transformer取代。后面我们也会对Transformer展开介绍。
