C++ 贪心 区间问题 最大不相交区间数

给定 N
个闭区间 [ai,bi]
，请你在数轴上选择若干区间，使得选中的区间之间互不相交（包括端点）。

输出可选取区间的最大数量。

输入格式
第一行包含整数 N
，表示区间数。

接下来 N
行，每行包含两个整数 ai,bi
，表示一个区间的两个端点。

输出格式
输出一个整数，表示可选取区间的最大数量。

数据范围
1≤N≤105
,
−109≤ai≤bi≤109
输入样例：
3
-1 1
2 4
3 5
输出样例：
2
首先这样选出来的的区间是没有交集的。

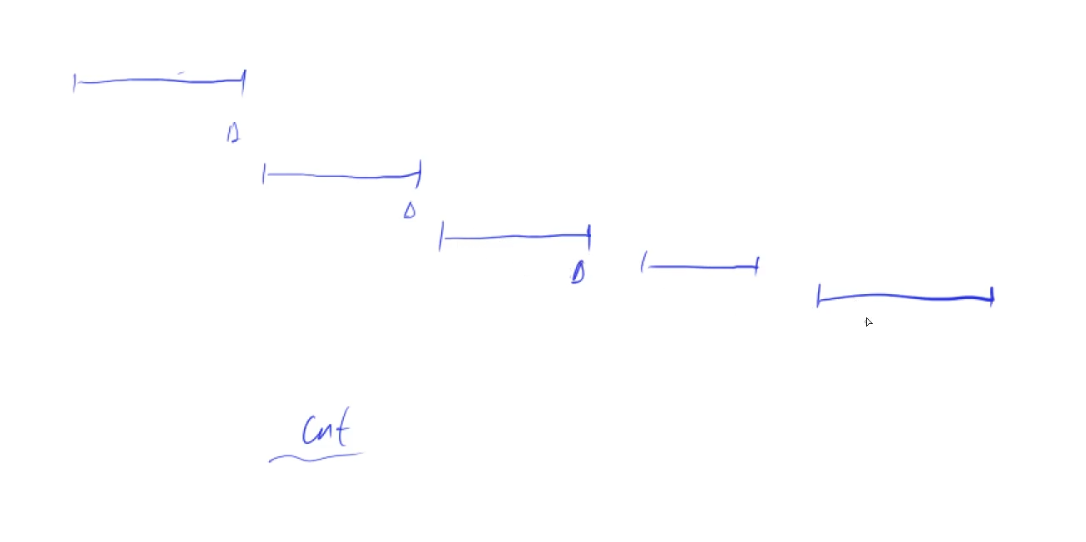
（1）这种选法一定是一种可行的选法。Ans≥cnt
（2）根据上一题C++ 贪心 区间问题 区间选点得出先选择的点覆盖掉了所有的区间。假如Ans > cnt，则至少还存在1个这样的区间可以选择，产生矛盾。则Ans ≤cnt。
证毕。

代码是一样的：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n;

struct Range
{
    int l, r;
    bool operator< (Range w)
    {
        return r < w.r;
    }
}range[N];

int main ()
{
    scanf("%d", &n);
    for(int i = 0; i < n; i ++ )
    {
        int l, r;
        scanf("%d%d", &l, &r);
        range[i] = {l, r};
    }
    
    sort(range, range + n);
    
    int res = 0, ed = -2e9; // res是答案，ed是上一个点的下标，因为一开始的时候一个点都没有选，赋值为负无穷
    for(int i = 0; i < n; i ++ ) // 枚举所有的区间
    {
        if(range[i].l > ed) // 如果说当前区间的左端点严格大于上一个选出来的右端点，就更新点
        {
            res ++;
            ed = range[i].r;
        }
    }
    
    printf("%d\n", res);
    
    return 0;
}