力扣231. 2 的幂（数学，二分查找，位运算）

Problem: 231. 2 的幂

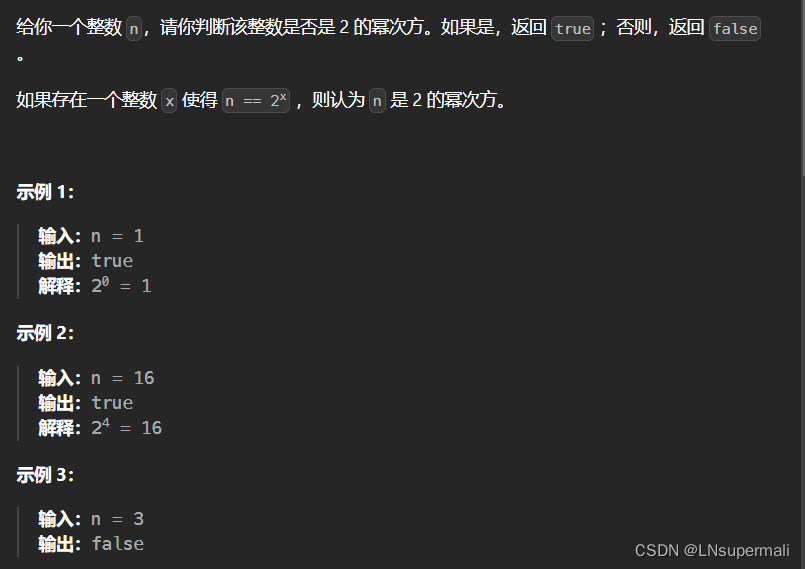
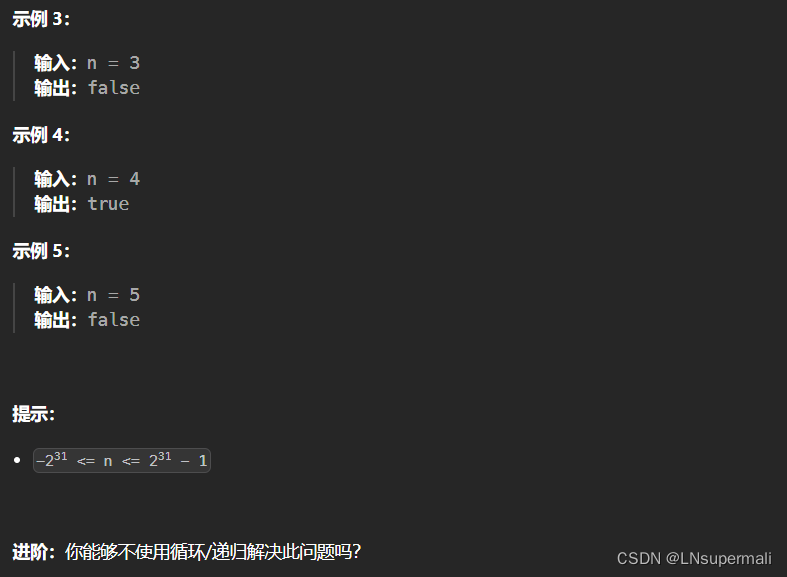
题目描述

思路即解法

思路1：位运算

1.易验证2的幂为正数；
2.易得2的幂用二进制表示只能有一个位为数字1
3.即将其转换为二进制统计其二进制1的个数

思路2：数学

当给定数n大于1时，每次当n模2等于0时（此时是2的幂）每次将n除以2最后判断n是否为1

思路3：二分查找

我们从0到$n$开始二分查找，每次取出当前的中间数mid，当$2^{\text{mid}}$,等于$n$时则返回true，否则继续二分查找；

复杂度

思路1：
时间复杂度:

$O(1)$

空间复杂度:

$O(1)$

思路2：
时间复杂度:

$O(1)$；因为在int范围内2的最大的幂为$2^{\text{30}}$

空间复杂度:

$O(1)$

思路：
时间复杂度:

$O(logn)$

空间复杂度:

$O(1)$

Code

思路1：

class Solution {
public:
    /**
     * Bit operation
     * @param n Given number
     * @return bool
     */
    bool isPowerOfTwo(int n) {
        if (n < 0) {
            return false;
        }
        int mask = 1;
        int count = 0;
        for (int i = 0; i < 32; ++i) {
            if ((n & mask) != 0) {
                count++;
            }
            mask <<= 1;
        }
        if (count == 1) {
            return true;
        }
        return false;
    }
};

思路2：

class Solution {
public:
    /**
     * Math
     * @param n Given number
     * @return bool
     */
    bool isPowerOfTwo(int n) {
        if (n < 0) {
            return false;
        }
        if (n > 1) {
            while (n % 2 == 0) {
                n /= 2;
            }
        }
        return n == 1 ? true : false;
    }
};
  

思路3：

class Solution {
public:
    /**
     * Binary Search
     * @param n Given number
     * @return bool
     */
    bool isPowerOfTwo(int n) {
        if (n < 1) {
            return false;
        }
        int start = 0;
        int end = n;
        while (start <= end) {
            int mid = start + (end - start) / 2;
            double result = (double)(pow(2, mid));
            if (result == n) {
                return true;
            } else if (result > n) {
                end = mid - 1;
            } else {
                start = mid + 1;
            }
        }
        return false;
    }
};