四、机器学习基础概念介绍

1_机器学习基础概念

机器学习一般可以分为训练和测试两个步骤。
训练：让模型学习数据的特点。
测试：让模型对新的数据进行预测，对比预测结果与实际结果之间的差异。
训练集：这批数据是供模型学习使用。
测试集：这批数据是供模型测试使用。
一般情况训练集和测试集是完全不相同的，训练集和测试集发生重叠是一个严重错误！

机器学习分类

1）按照学习方式

• 有监督学习：训练数据包含了数据本身及其对应的标签。每个训练数据都有一个明确的标识或结果。
• 无监督学习：训练数据只包含数据本身，不包含对应的标签。例如通过聚类算法对很多段EEG信号进行聚类分析。模型能够自主的学习到一些数据的特点。（通常缺乏先验知识，因此难以对数据进行标注或者标注成本太高）
• 半监督学习：部分训练数据有标签，部分训练数据没有标签。
• 强化学习：强化学习的标签可以不是一个明确的标识或结果。 一般是一个反馈或者奖励。

2）按照算法的原理

• 传统的机器学习(不包含任何人工神经网络结构，此文章的重点)
• 深度学习

1.1 有监督学习

监督学习一般解决两个问题：分类和回归
1） 分类和回归是做什么的

• 无论是分类还是回归，其本质都是对输入进行预测，都是有监督学习。
• 分类是根据输出得到一个分类的类别，而回归是根据输出得到一个具体的值。

2）分类和回归的区别

• 分类问题的输出的物体所属的类别，而回归问题的输出是物体的值。
• 分类问题的输出是离散值（0，1，2，3,…），回归问题输出的是连续值（36.7,36.8,…）
• eg:输入是一堆气象数据：
  如果输出是具体的天气情况：雨天？晴天？阴天？ —分类—
  如果输出是具体的温度？ —回归—

3）有监督学习有哪些

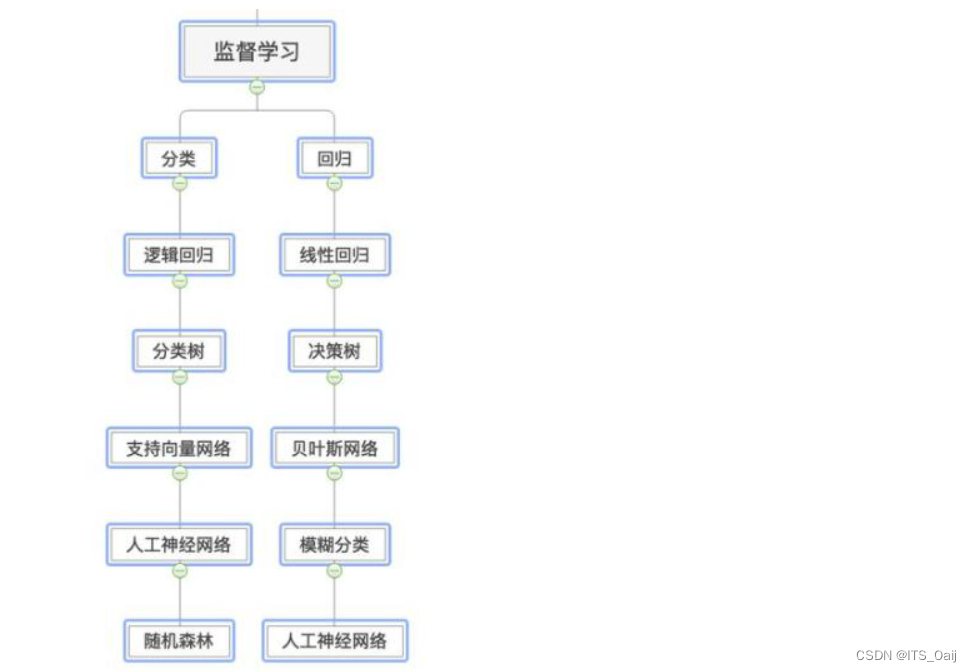
1.2 无监督学习

无监督学习一般解决两个问题：聚类和降维
1）聚类

• 在无监督学习中，数据不会带有任何标签。将这些无标签数据分成N个分开点集（称为簇）的算法，就被称为聚类算法。
• 常用聚类算法：K均值聚类和层次聚类
• 聚类和分类的区别：分类是有标签的，每个物体有其具体的明确的归属。而聚类是没有标签的，根据算法不同可能会得到不通过的结果。

2）降维

• 采用某种映射方法,将原高维空间中的数据点映射到低维度的空间中。
• 降维是对数据本身处理，不需要标签。
• 常用降维算法：PCA、张量分解。

2_有监督机器学习—常见评估方法

常见的评估方法有：留出法、校验验证法和自助法

数据集的划分

• 第一种：训练集和测试集（不建议适用）
• 第二种：训练集、验证集和测试集（正确的数据集划分方法）

训练集——学生的课本；学生 根据课本里的内容来掌握知识。
验证集——作业，通过作业可以知道 不同学生学习情况、进步的速度快慢。
测试集——考试，考的题是平常都没有见过，考察学生举一反三的能力。

正确做法： 在训练集上训练模型，在验证集上评估模型（对模型进行参数调整），最后在测试集上测试模型。

2.1 留出法

• 将数据集D分割为两个互斥的集合：训练集S和测试集T。
• 其中训练集S还可以进一步划分为训练集S1和验证集V。
• 数据集划分完毕后，直接在训练集S上训练模型，在验证集S1上评估模型，在测试集T上测试模型即可。

一般情况下，会选择20%左右的数据作为测试集。
缺点：数据选择随机，结果的方差比较大

2.2 校验验证法（重点方法）

校验验证法：能充分利用数据集，但不适用于特别大的数据集

• 一般分为：简单交叉验证，留一法交叉验证和K折交叉验证
• 其中，K折交叉验证（单独流出测试集）（该方法为常用方法，Sklearn的默认方法）

简单交叉验证

• 将样本全部打乱，随机的将样本数据集分为互斥的两个部分：训练集和测试集。其中训练集还可以划分为训练集和验证集。
• 通过训练集训练模型，通过验证集选择模型参数，在测试集上评估模型的分类率。
• 接着重新把样本数据打乱，重新划分训练集和测试集。重复上述过程若干次，此时将会得到若千个分类率。
• 选择最大的分类率作为最终分类率。

等价于将留出法重复n次，通常用于模型预筛，可作为论文中探讨模型选择的一部分。

K折交叉验证（单独流出测试集）（常用方法/Sklearn的默认方法）

• 将样本全部打乱，随机从样本数据集划分出互斥的两部分：训练集和测试集。从训练集D分类K大小相似的互斥子集。
• 每次选用K-1个子集作为训练集，余下的那个子集作为验证集。这样就得到了K组训练/验证集，从而可以进行 K次训练和验证，可以返回K个模型。
• 在测试集上分别对K个模型进行测试得到分类率，最终K次测试中分类率的均值作为最终分类率。

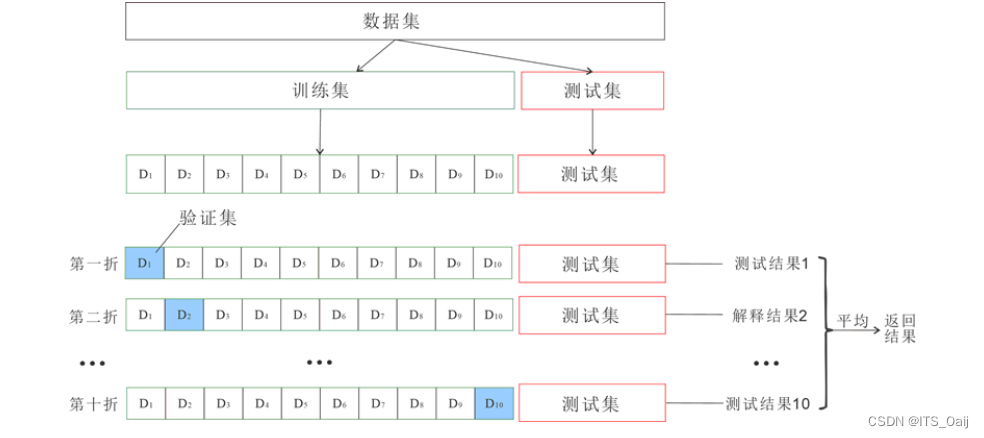k为几就是几折交叉验证，通常五折/十折。

k折交叉验证（不单独留出测试集）

• 单独留出测试集的交叉验证会在进行交叉验证前单独留出测试集，后续所有的交叉验证都会最终在测试集上进行测试。
• 而不单独留出测试集的折交叉验证不会单独留出测试集，训练集、验证集和测试集将一会通过“交叉”产生。
• 数据量比较多，10折。10000个样本，

留一法交叉验证

• 当K折交叉验证中的K与样本个数N相等时，此时该验证方法被称为“留一法”。
• 理论上，留一法对数据的利用最为充分，其结果最接近实际的结果。如果样本数据比较大，会带来极大的计算量，因此留一法一般只适用于小样本量数据集。最终K个模型分类率的均值作为最终分类率。
• 注意：在神经科学领域，一般使用留一被试法
• 留一被试法：将同一个被试的所有的样本视为一个特定的集合，每次选择一个被试的样本作为测试集，其他被试的样本作为训练集。

Subject-wise交叉验证

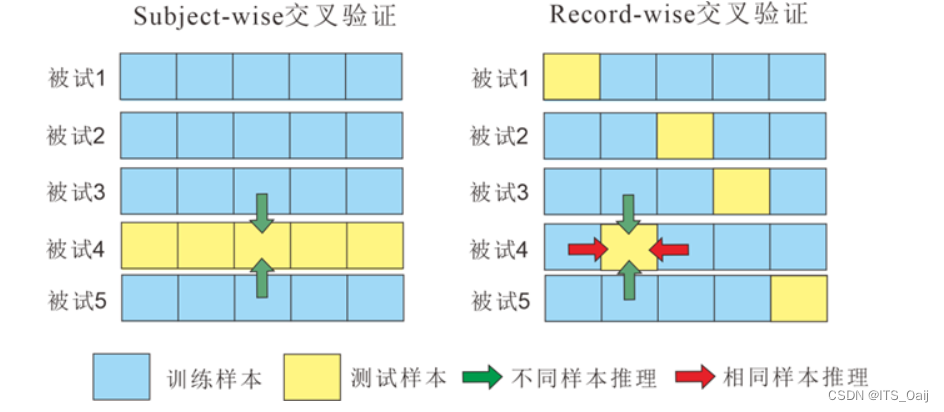
2.3 bootstrap自助法

3_ 有监督机器学习—学习评价指标

3.1 准确率（Accuracy）

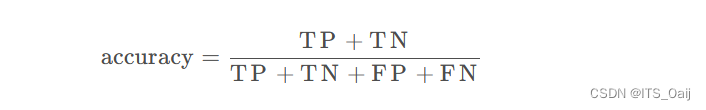
准确率能够清晰的判断我们模型的表现，但有一个严重的缺陷： 在正负样本不均衡的情况下，占比大的类别往往会成为影响 Accuracy 的最主要因素，此时的 Accuracy 并不能很好的反映模型的整体情况。
例如，一个测试集有正样本99个，负样本1个。模型把所有的样本都预测为正样本，那么模型的Accuracy为99%，看评价指标，模型的效果很好，但实际上模型没有任何预测能力。

混淆矩阵

TP = True Postive = 真阳性； FP = False Positive = 假阳性
FN = False Negative = 假阴性； TN = True Negative = 真阴性
比如我们一个模型对15个样本进行预测，然后结果如下。
真实值：0 1 1 0 1 1 0 0 1 0 1 0 1 0 0
预测值：1 1 1 1 1 0 0 0 0 0 1 1 1 0 1

3.2 精确率（Precision）

精度（precision, 或者PPV,，positive predictive value) = TP / (TP + FP)
在上面的例子中，精度=5/(5+4)= 0.556

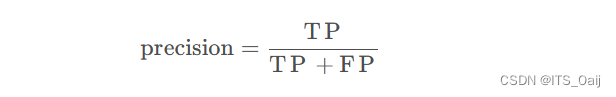
3.3 召回率（Recall）

·召回（recall，或者敏感度，sensitivity，真阳性率，TPR，True Positive Rate)= TP /(TP +FN)
在上面的例子中，召回=5/(5+2) = 0.714

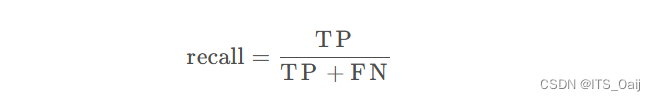
3.4 特异度（Specificity）

特异度（specificity，或者真阴性率，TNR，True Negative Rate) = TN / (TN + FP)
在上面的例子中，特异度 = 4 / (4+2) = 0.667

3.5 F1-值（F1-score）

F1-值(F1-score) = 2TP / (2TP+FP+FN)
精确率和召回率是一对矛盾的指标，因此需要放到一起综合考虑。F1-score是精确率和召回率的调和平均值。
相对于ACC的优势：能够同时表明模型对正负样本的预测能力
在上面的例子中，F1-值 = 25 / (25+4+2) = 0.625

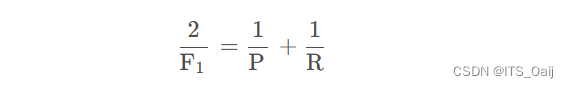
• 敏感度和特异度有何用？
  特异度(specificity)，TNR,即它反映筛检试验确定非病人的能力。
  敏感度(sensitivity，召回率)，TPR,即它反映筛检试验确定病人的能力。
  敏感度高=漏诊率低，特异度高=误诊率低。
  例如：核酸检测允许比较高的误诊率，但漏诊率低一定要很低。

3,6 ROC曲线

ROC曲线（横轴：FPR；纵轴：TPR）该曲线越接近左上角越好
TPR = TP / (TP+FN); 真阳率
FPR = FP / (FP + TN); 伪阳率

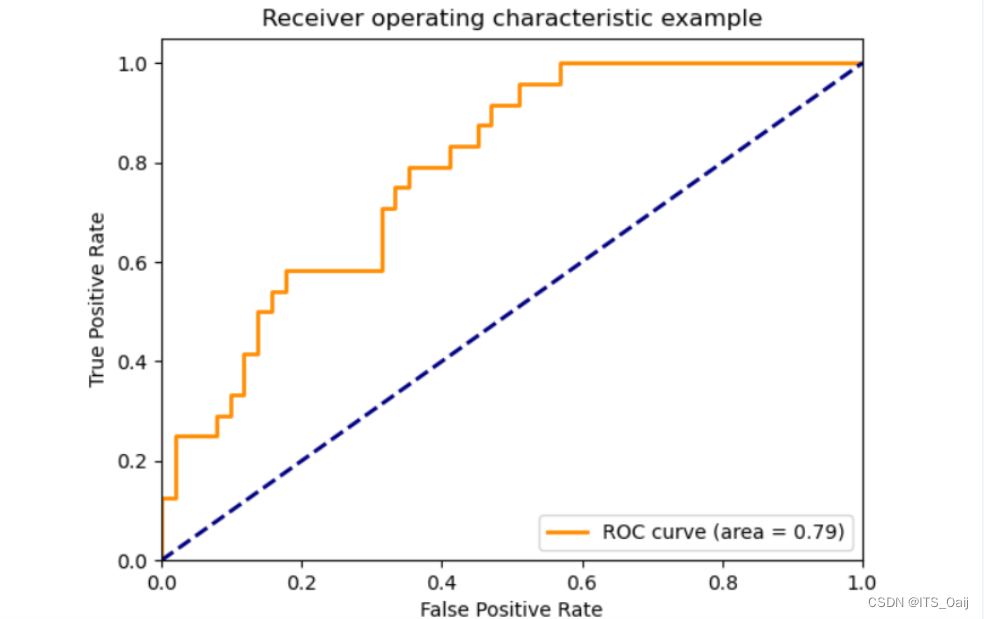
3.7 AUC面积

AUC（ROC与坐标轴围成图像的面积）
AUC = 1，是完美分类器。
AUC = [0.85, 0.95], 效果很好
AUC = [0.7, 0.85], 效果一般
AUC = [0.5, 0.7],效果较低，但用于预测股票已经很不错了
AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

3.8 PR曲线

（仅供了解，横轴是recall，纵轴是precision，越接近右上角越好）