Chapter7.1：频域分析法理论基础

该系列博客主要讲述Matlab软件在自动控制方面的应用，如无自动控制理论基础，请先学习自动控制系列博文，该系列博客不再详细讲解自动控制理论知识。
自动控制理论基础相关链接：https://blog.csdn.net/qq_39032096/category_10287468.html?spm=1001.2014.3001.5482
博客参考书籍：《MATLAB/Simulink与控制系统仿真》。

1.频域分析法理论基础

1.1 频率特性基本概念

1.1.1 频率特性概述

• 控制系统的频率特性反映的是系统对正弦输入信号的响应性能；
• 频域分析法可以通过试验直接求得频率特性来分析系统的品质，应用频率特性分析系统可以得出定性和定量的结论，并具有明显的物理含义；
• 采用频率特性作为数学模型来分析和设计系统的方法称为频率特性法，亦称频率响应法；
• 频率响应法的基本思想：把控制系统中的各个变量看成一些信号，这些信号又由很多不同频率的正弦信号合成，各个变量的运动就是系统对各个不同频率的信号的响应的总和；

1.1.2 频率特性定义

频率特性：指系统在正弦信号作用下，稳态输出与输入之比相对频率的关系特性；

频率特性函数：
$$G(\mathrm{j}\omega )=\frac{X_o(\mathrm{j}\omega )}{X_i(\mathrm{j}\omega )}=A(\omega ){\mathrm{e}}^{\mathrm{j}\phi (\omega )}$$
其中：$A(\omega )=\frac{X_o(\omega )}{X_i(\omega )}$称为幅频特性，$\phi (\omega )={\phi }_o(\omega )-{\phi }_i(\omega )$称为相频特性；

频率特性亦表示为：
$$G(\mathrm{j}\omega )=\frac{X_o(\mathrm{j}\omega )}{X_i(\mathrm{j}\omega )}=p(\omega )+\mathrm{j}\theta (\omega )$$
其中：$p(\omega )$为$G(\mathrm{j}\omega )$的实部，称为实频特性，$\theta (\omega )$为$G(\mathrm{j}\omega )$的虚部，称为虚频特性；

有如下关系：
$$\{\begin{array}{llc}& p(\omega )=A(\omega )\cos \phi (\omega )，& \theta (\omega )=A(\omega )\sin \phi (\omega )\\ & & \\ & A(\omega )=\sqrt{p^2(\omega )+{\theta }^2(\omega )}，& \phi (\omega )=\arctan \frac{\theta (\omega )}{p(\omega )}\end{array}$$
当输入为非正弦周期信号，其输入可利用傅里叶级数展开成正弦波的叠加，其输出为相应的正弦波的叠加；此时系统频率特性定义为系统输出量的傅氏变换与输入量的傅氏变换之比；

1.1.3 频域分析法特点

• 适用于各环节、开环和闭环系统的性能分析。

  运用奈奎斯特稳定判据，通过作图方法，可以根据系统开环频率特性分析闭环系统的稳定性及性能，不必求解系统的特征根，从而避免直接求解微分方程的困难；

• 频率特性有明确的物理意义。

  很多元部件频率特性可以用实验方法确定，对于机理复杂或机理不明难以写出微分方程的元部件或系统，在实验室中采用信号发生器和精密测量仪器，可以测出其频率特性；

• 频域性能指标和时域性能指标有确定的对应关系。

  对于二阶系统，频率特性与时域过渡过程性能指标有确定的对应关系，对于高阶系统，通过把系统参数和结构的变化与时域过渡过程指标联系起来，存在着近似的对应关系；

• 频率设计可兼顾动态响应和噪声抑制两方面的要求。

  当系统在某些频率范围内存在严重的噪声时，应用频率分析法可以设计处能满意地抑制这些噪声的系统；

• 在校正方法中，频域分析法校正十分方便。

  当系统的性能指标以幅值裕度、相位裕度和误差系数等形式给出时，采用频率分析法来分析和设计系统十分方便；

• 频率法不能全面分析非线性系统。

  频率法主要应用于单输入单输出的线性定常系统的分析研究中，在多输入多输出的线性定常系统中也有应用；在非线性中只有某些局部典型的应用，不能对非线性系统进行全面的分析；

1.1.4 频域性能指标

• 谐振频率${\omega }_r$：表示幅频特性$A(\omega )$出现最大值时对应的频率；
• 谐振峰值$M_r$：表示幅频特性的最大值，$M_r$值大表明系统对频率的正弦信号反应强烈，即系统平稳性差，阶跃响应超调量大；
• 频带${\omega }_b$：表示幅频特性$A(\omega )$的幅值衰减到初始值的$0.707$倍对应的频率；${\omega }_b$大表明系统复现快速变化信号的能力强，失真小，即系统快速性好，阶跃响应上升时间短，调节时间短；
• 零频$A(0)$：表示频率$\omega =0$时的幅值；$A(0)$表示系统阶跃响应的终值，$A(0)$与$1$间的差反映系统的稳态精度，$A(0)$越接近$1$，系统精度越高；

1.2 频率特性的表示方法

1.2.1 极坐标图(Nyquist图)

• 系统频率特性表示：
  $$G(\mathrm{j}\omega )=A(\omega ){\mathrm{e}}^{\mathrm{j}\phi (\omega )}$$

• 用向量表示某一频率${\omega }_i$下的$G(\mathrm{j}{\omega }_i)$向量的长度$A({\omega }_i)$，向量极坐标角为$\phi ({\omega }_i)$，$\phi ({\omega }_i)$正方向取逆时针，选极坐标与直角坐标重合，极坐标的顶点在坐标原点，如下图所示：

  

• 频率特性$G(\mathrm{j}\omega )$是输入频率$\omega$的复变函数，当频率$\omega$由$0\to \infty$时，$G(\mathrm{j}\omega )$变化的曲线，即向量端点轨迹，称为极坐标图；

• 极坐标图中，当$\omega ={\omega }_i$时，在实轴上的投影即为实频特性$p({\omega }_i)$，在虚轴上的投影即为虚频特性；

1.2.2 对数坐标图(Bode图)

• $\mathrm{Bode}$图由对数幅频特性和对数相频特性组成，如下图所示：

  

• 对数幅频特性是频率特性的对数值$\mathrm{L}(\omega )=20\lg \mathrm{A}(\omega )$与频率$\omega$的关系曲线，对数相频特性是频率特性的相角$\phi (\omega )$与频率$\omega$的关系曲线；

• 对数幅频特性纵轴为$\mathrm{L}(\omega )=20\lg A(\omega )$，单位为$\mathrm{dB}$(分贝)，采用线性分度，$\mathrm{A}(\omega )$每增加$10$倍，$\mathrm{L}(\omega )$增加$20\mathrm{dB}$，横坐标采用对数分度，即横轴上的$\omega$取对数后为等分点；

• 对数相频特性横轴采用对数分度，纵轴采用线性分度，单位为°(度)；

• 对数坐标图($\mathrm{Bode}$图)的优点：

  • 将幅值相乘化为对数相加运算，极大地简化了系统频率特性的绘制工作；
  • 横轴采用对数分度，缩小了比例尺，扩大了频率视野，可以在较大的频段范围内表示系统频率特性；在一张$\mathrm{Bode}$图上，既可以绘制频率特性的中、高频段，也能绘制低频段，有利于系统的分析和设计；
  • 可以绘制渐近的对数幅频特性，亦可制作标准样板，绘制精确的对数频率特性；

1.2.3 对数幅相图(Nichols图)

• 对数幅相图亦称为$\mathrm{Nichols}$图，是将对数幅频特性和相频特性在角频率为参变量情况下合成为一张图；

• 对数幅相图如下所示：

  

• $\mathrm{Nichols}$图特点：纵轴为$\mathrm{L}(\omega )=20\lg \mathrm{A}(\omega )$，单位为$\mathrm{dB}$(分贝)，采用线性分度；横坐标采用对数分度，单位为°(度)，频率$\omega$为参变量；

1.3 典型环节的频率特性

1.3.1 典型环节

典型环节分为：最小相位环节和非最小相位环节；

最小相位环节：

• 比例环节：$K，(K>0)$；
• 惯性环节：$1/(Ts+1)，(T>0)$；
• 一阶微分环节：$Ts+1，(T>0)$；
• 振荡环节：$1/(s^2/{\omega }_n^2+2\zeta s/{\omega }_n+1)，({\omega }_n>0，0\le \zeta <1)$；
• 二阶微分环节：$s^2/{\omega }_n^2+2\zeta s/{\omega }_n+1，({\omega }_n>0，0\le \zeta <1)$；
• 积分环节：$1/s$；
• 微分环节：$s$；

非最小相位环节：

• 比例环节：$K，(K<0)$；
• 惯性环节：$1/(-Ts+1)，(T>0)$；
• 一阶微分环节：$-Ts+1，(T>0)$；
• 振荡环节：$1/(s^2/{\omega }_n^2-2\zeta s/{\omega }_n+1)，({\omega }_n>0，0<\zeta <1)$；
• 二阶微分环节：$s^2/{\omega }_n^2-2\zeta s/{\omega }_n+1，({\omega }_n>0，0<\zeta <1)$；

开环传递函数的典型环节分解可将开环系统表示为若干个典型环节的串联形式：
$$G(s)H(s)=\prod _{i=1}^N{G}_i(s)$$
设典型环节的频率特性为：
$$G_i(j\omega )=A_i(\omega ){\mathrm{e}}^{j{\phi }_i(\omega )}$$
则系统开环频率特性为：
$$G(j\omega )H(j\omega )=\left[\prod _{i=1}^N{A}_i(\omega )\right]{\mathrm{e}}^{j\left[{\sum }_{i=1}^N{\phi }_i(\omega )\right]}$$
系统开环幅频特性和开环相频特性为：
$$A(\omega )=\prod _{i=1}^N{A}_i(\omega )，\phi (\omega )=\sum _{i=1}^N{\phi }_i(\omega )$$
系统开环对数幅频特性为：
$$L(\omega )=20\lg A(\omega )=\sum _{i=1}^{N}20\lg A_i(\omega )=\sum _{i=1}^N{L}_i(\omega )$$

• 系统开环频率特性表现为组成开环系统的诸典型环节频率特性的合成；
• 系统开环对数频率特性，表现为诸典型环节对数频率特性叠加；

1.3.2 典型环节的频率特性

典型环节频率特性曲线的若干特点：

1. 非最小相位与对应的最小相位环节

   最小相位的比例环节$G(s)=K(K>0)$，简称比例环节，幅频和相频特性如下：
   $$A(\omega )=K，\phi (\omega )=0°$$
   非最小相位的比例环节$G(s)=-K(K>0)$，幅频和相频特性如下：
   $$A(\omega )=K，\phi (\omega )=-180°$$
   最小相位的惯性环节$G(s)=\frac{1}{Ts+1}，(T>0)$，幅频和相频特性为：
   $$A(\omega )=\frac{1}{\sqrt{1+T^2{\omega }^2}}，\phi (\omega )=-\arctan T\omega$$
   非最小相位的惯性环节$G(s)=\frac{1}{-Ts+1}，(T>0)$，幅频和相频特性为：
   $$A(\omega )=\frac{1}{\sqrt{1+T^2{\omega }^2}}，\phi (\omega )=\arctan T\omega$$

   • 最小相位惯性环节和非最小相位的惯性环节，幅频特性相同，相频特性符号相反，幅相曲线关于实轴对称；
   • 最小相位惯性环节和非最小相位惯性环节，对数幅频曲线相同，对数相频曲线关于0°线对称；
   • 上述两点特点，对于振荡环节和非最小相位振荡环节、一阶微分环节和非最小相位一阶微分环节、二阶微分环节和非最小相位二阶微分环节均适用；

2. 传递函数互为倒数的典型环节

   最小相位典型环节中，积分环节和微分环节、惯性环节和一阶微分环节、振荡环节和二阶微分环节的传递函数互为倒数，有如下关系：
   $$G_1(s)=\frac{1}{G_2(s)}$$
   设$G_1(j\omega )=A_1(\omega ){\mathrm{e}}^{j{\phi }_1(\omega )}$，则有：
   $$\{\begin{array}{ll}& {\phi }_2(\omega )=-{\phi }_1(\omega )\\ & \\ & L_2(\omega )=20\lg A_2(\omega )=20\lg \frac{1}{A_1(\omega )}=-L_1(\omega )\end{array}$$
   传递函数互为倒数的典型环节，对数幅频曲线关于0dB线对称，对数相频曲线关于0°线对称；此结论在非最小相位环节中亦适用；

3. 振荡环节和二阶微分环节

   振荡环节的传递函数为：
   $$G(s)=\frac{1}{(s/{\omega }_n{)}^2+2\zeta (s/{\omega }_n)+1}；{\omega }_n>0，0<\zeta <1$$
   振荡环节的频率特性：
   $$A(\omega )=\frac{1}{\sqrt{{\left(\begin{array}{c}1-\frac{{\omega }^2}{{\omega }_n^2}\end{array}\right)}^2+4{\zeta }^2\frac{{\omega }^2}{{\omega }_n^2}}}$$

   $$\phi (\omega )=-\arctan \frac{2\zeta \frac{\omega }{{\omega }_n}}{1-\frac{{\omega }^2}{{\omega }_n^2}}=\{\begin{array}{ll}& -\arctan \frac{2\zeta \frac{\omega }{{\omega }_n}}{1-\frac{{\omega }^2}{{\omega }_n^2}}，\omega \le {\omega }_n\\ & \\ & -\left(\begin{array}{c}180-\arctan \frac{2\zeta \frac{\omega }{{\omega }_n}}{\frac{{\omega }^2}{{\omega }_n^2}-1}\end{array}\right)，\omega >{\omega }_n\end{array}$$

   $\phi (0)=0°，\phi (\infty )=-180°$，相频特性曲线从0°单调减至-180°；当$\omega ={\omega }_n$时，$\phi ({\omega }_n)=-90°$，$A({\omega }_n)=\frac{1}{2\zeta }，$振荡环节与虚轴的交点为$-\mathrm{j}\frac{1}{2\zeta }$；

   $A(0)=1，A(\infty )=0$，求$A(\omega )$的极值，
   $$\frac{\mathrm{d}A(\omega )}{\mathrm{d}\omega }=\frac{-\left[-\frac{2\omega }{{\omega }_n^2}\left(1-\frac{{\omega }^2}{{\omega }_n^2}\right)+4{\zeta }^2\frac{\omega }{{\omega }_n^2}\right]}{{\left[{\left(1-\frac{{\omega }^2}{{\omega }_n^2}\right)}^2+4{\zeta }^2\frac{{\omega }^2}{{\omega }_n^2}\right]}^{\frac{3}{2}}}=0$$
   得谐振频率：
   $${\omega }_r={\omega }_n\sqrt{1-2{\zeta }^2}，0<\zeta \le \sqrt{2}/2$$
   谐振峰值：
   $$M_r=A({\omega }_r)=\frac{1}{2\zeta \sqrt{1-{\zeta }^2}}，0<\zeta \le \sqrt{2}/2$$
   当$0<\zeta <\frac{\sqrt{2}}{2}$时，
   $$\frac{\mathrm{d}{M}_r}{\mathrm{d}\zeta }=\frac{-(1-2{\zeta }^2)}{{\zeta }^2(1-{\zeta }^2{)}^{\frac{3}{2}}}<0$$
   ${\omega }_r，M_r$均为阻尼比$\zeta$的减函数$(0<\zeta \le \frac{\sqrt{2}}{2})$；当$0<\zeta <\frac{\sqrt{2}}{2}$时，且$\omega \in (0,{\omega }_r)$时，$A(\omega )$单调增；$\omega \in ({\omega }_r,\infty )$时，$A(\omega )$单调减；当$\frac{\sqrt{2}}{2}<\zeta <1$时，$A(\omega )$单调减；

   二阶微分环节的传递函数为振荡环节传递函数的倒数，按对称性可得二阶微分环节的对数频率曲线，有：
   $$\{\begin{array}{ll}& A(0)=1\\ & \phi (0)=0°\end{array}，\{\begin{array}{ll}& A({\omega }_n)=2\zeta \\ & \phi ({\omega }_n)=90°\end{array}，\{\begin{array}{ll}& A(\infty )=\infty \\ & \phi (\infty )=180°\end{array}$$
   当阻尼比$\frac{\sqrt{2}}{2}<\zeta <1$时，$A(\omega )$从1单调增至$\infty$；当阻尼比$0<\zeta <\frac{\sqrt{2}}{2}$，且$\omega \in (0,{\omega }_r)$时，$A(\omega )$从1单调减至
   $$\{\begin{array}{ll}& A({\omega }_r)=2\zeta \sqrt{1-{\zeta }^2}<1\\ & {\omega }_r=\omega \sqrt{1-2{\zeta }^2}\end{array}$$
   在$\omega \in ({\omega }_r,\infty )$时，$A(\omega )$单调增；

4. 对数幅频渐近特性曲线

   为简化惯性环节、一阶微分环节、振荡环节和二阶微分环节的对数幅频曲线的作图，常用低频和高频渐近线近似表示对数幅频曲线，称为对数幅频渐近特性曲线；

   惯性环节的对数幅频渐近特性为：
   $$L_a(\omega )=\{\begin{array}{ll}0,& \omega <\frac{1}{T}\\ -20\lg \omega T，& \omega >\frac{1}{T}\end{array}$$
   

   低频部分是零分贝线，高频部分是斜率为$-20dB/dec$的直线，两条直线交于$\omega =\frac{1}{T}$处，称频率$\frac{1}{T}$为惯性环节的交接频率；用渐近特性近似表示对数幅频特性存在误差：$\Delta L(\omega )=L(\omega )-L_a(\omega )$，在交接频率处误差最大，约为$-3\mathrm{dB}$；一阶微分环节和非最小相位一阶微分环节与惯性环节的对数幅频渐近特性曲线以$0\mathrm{dB}$线互为镜像；

   振荡环节的对数幅频特性为：
   $$L(\omega )=-20\lg \sqrt{{\left(1-\frac{{\omega }^2}{{\omega }_n^2}\right)}^2+4{\zeta }^2\frac{{\omega }^2}{{\omega }_n^2}}$$
   当$\omega <<{\omega }_n$时，$L(\omega )\approx 0$，低频渐近线为0dB线；当$\omega >>{\omega }_n$时，$L(\omega )=-40\lg \frac{\omega }{{\omega }_n}$，高频渐近线为过$({\omega }_n,0)$点，斜率为-40dB/dec的直线，振荡环节的交接频率为${\omega }_n$，对数幅频渐近特性为：
   $$L_a(\omega )=\{\begin{array}{ll}0,& \omega <{\omega }_n\\ -40\lg \frac{\omega }{{\omega }_n},& \omega >{\omega }_n\end{array}$$
   非最小相位振荡环节与振荡环节对数幅频渐近特性曲线相同，二阶微分环节和非最小相位二阶微分环节与振荡环节的对数幅频渐近特性曲线关于0dB线对称；

   半对数坐标系中的直线方程为：
   $$k=\frac{L_a({\omega }_2)-L_a({\omega }_1)}{\lg {\omega }_2-\lg {\omega }_1}$$
   其中：$[{\omega }_1,\lg ({\omega }_1)]、[{\omega }_2,\lg ({\omega }_2)]$为直线上的两点，$k(dB/dec)$为直线斜率；

1.3.3 开环幅相特性曲线

绘制概略开环幅相特性曲线的方法：

• 开环幅相特性曲线的起点$(\omega =0_{+})$和终点$(\omega =\infty )$；

• 开环幅相特性曲线与实轴的交点。设$\omega ={\omega }_x$时，$G(\mathrm{j}{\omega }_x)H(\mathrm{j}{\omega }_x)$的虚部为：
  $$\mathrm{Im}[G(\mathrm{j}{\omega }_x)H(\mathrm{j}{\omega }_x)]=0或\phi ({\omega }_x)=\angle [G(\mathrm{j}{\omega }_x)H(\mathrm{j}{\omega }_x)]=k\pi ，k=0,\pm 1，\pm 2，\dots$$
  其中：${\omega }_x$称为穿越频率；

  开环频率特性曲线与实轴交点坐标值为：
  $$\mathrm{Re}[G(\mathrm{j}{\omega }_x)H(\mathrm{j}{\omega }_x)]=G(\mathrm{j}{\omega }_x)H(\mathrm{j}{\omega }_x)$$

• 开环幅相特性曲线的变化范围(象限、单调性)；

绘制概略开环幅相特性曲线规律小结：

• 开环幅相特性曲线的起点，取决于比例环节$K$和系统积分或微分环节的个数$\nu$(系统型别)；

  • $\nu <0$，起点为原点；
  • $\nu =0$，起点为实轴上的点$K$处，$K$为系统开环增益，$K$有正负之分；
  • $\nu >0$，设$\nu =4k+i(k=0,1,2,\dots ;i=1,2,3,4)，$则$K>0$时为$i\times (-90°)$的无穷远处，$K<0$时为$i\times (-90°)-180°$的无穷远处；

• 开环幅相特性曲线的终点，取决于开环传递函数分子、分母多项式中最小相位环节和非最小相位环节的阶次和；

  设系统开环传递函数的分子、分母多项式的阶次分别为$m$和$n$，记除$K$外，分子多项式中最小相位环节的阶次和为$m_1$，非最小相位环节的阶次和为$m_2$，分母多项式中最小相位环节的阶次和为$n_1$，非最小相位环节的阶次和为$n_2$，则有：
  $$m=m_1+m_2,n=n_1+n_2$$

  $$\phi (\infty )=\{\begin{array}{ll}[(m_1-m_2)-(n_1-n_2)]\times 90°，& K>0\\ & \\ [(m_1-m_2)-(n_1-n_2)]\times 90°-180°,& K<0\end{array}$$

  当开环系统为最小相位系统时，若：
  $$\begin{array}{rlrl}& n=m,& & G(\mathrm{j}\infty )H(\mathrm{j}\infty )=K^{\ast }\\ & & & \\ & n>m,& & G(\mathrm{j}\infty )H(\mathrm{j}\infty )=0\angle [(n-m)\times (-90°)]\end{array}$$
  其中：$K^{\ast }$为系统开环根轨迹增益；

• 若开环系统存在等幅振荡环节，重数$l$为正整数，即开环传递函数具有如下形式：
  $$G(s)H(s)=\frac{1}{(\frac{s^2}{{\omega }_n^2}+1{)}^l}{G}_1(s)H_1(s)$$
  $G_1(s)H_1(s)$不含$\pm \mathrm{j}{\omega }_n$的极点，则当$\omega$趋于${\omega }_n$时，$A(\omega )$趋于无穷，而：
  $$\begin{array}{rl}& \phi ({\omega }_{n^{-}})\approx {\phi }_1({\omega }_n)=\angle [G_1(j{\omega }_n)H_1(j{\omega }_n)]\\ & \\ & \phi ({\omega }_{n^{+}})\approx {\phi }_1({\omega }_n)-l\times 180°\end{array}$$
  即$\phi (\omega )$在$\omega ={\omega }_n$附近，相角突变$-l\times 180°$；

1.3.4 开环对数频率特性曲线

系统开环对数幅频渐近特性：
$$L_a(\omega )=\sum _{i=1}^N{L}_{a_i}(\omega )$$
对于任意的开环传递函数，按典型环节分解，将组成系统的典型环节分为三部分：

• $\frac{K}{s^{\nu }}$或$\frac{-K}{s^{\nu }}(K>0)$；
• 一阶环节，包括惯性环节、一阶微分环节及对应的非最小相位环节，交接频率为$\frac{1}{T}$；
• 二阶环节，包括振荡环节、二阶微分环节及对应的非最小相位环节，交接频率为${\omega }_n$；

记${\omega }_{\min }$为最小交接频率，称$\omega <{\omega }_{\min }$的频率范围为低频段；

开环对数幅频渐近特性曲线绘制步骤：

1. 开环传递函数典型环节分解；

2. 确定一阶环节、二阶环节的交接频率，将各交接频率标注在半对数坐标图的$\omega$轴上；

3. 绘制低频段渐近特性线：在$\omega <{\omega }_{\min }$频段内，开环系统幅频渐近特性的斜率取决于$\frac{K}{{\omega }^{\nu }}$，因而直线斜率为$-20\nu dB/dec$；获得低频渐近线，需要确定直线上的一点，方法如下：

   • 方法1：在$\omega <{\omega }_{\min }$范围内，任选一点${\omega }_0$，计算$L_a({\omega }_0)=20\lg K-20\nu \lg {\omega }_0$；
   • 方法2：取频率为特定值${\omega }_0=1$，则$L_a(1)=20\lg K$；
   • 方法3：取$L_a({\omega }_0)$为特殊值0，有$\frac{K}{{\omega }_0^{\nu }}=1$，则${\omega }_0=K^{\frac{1}{\nu }}$；

   过点$({\omega }_0,L_a({\omega }_0))$在$\omega <{\omega }_{\min }$范围内可作斜率为-20$\nu$dB/dec的直线；

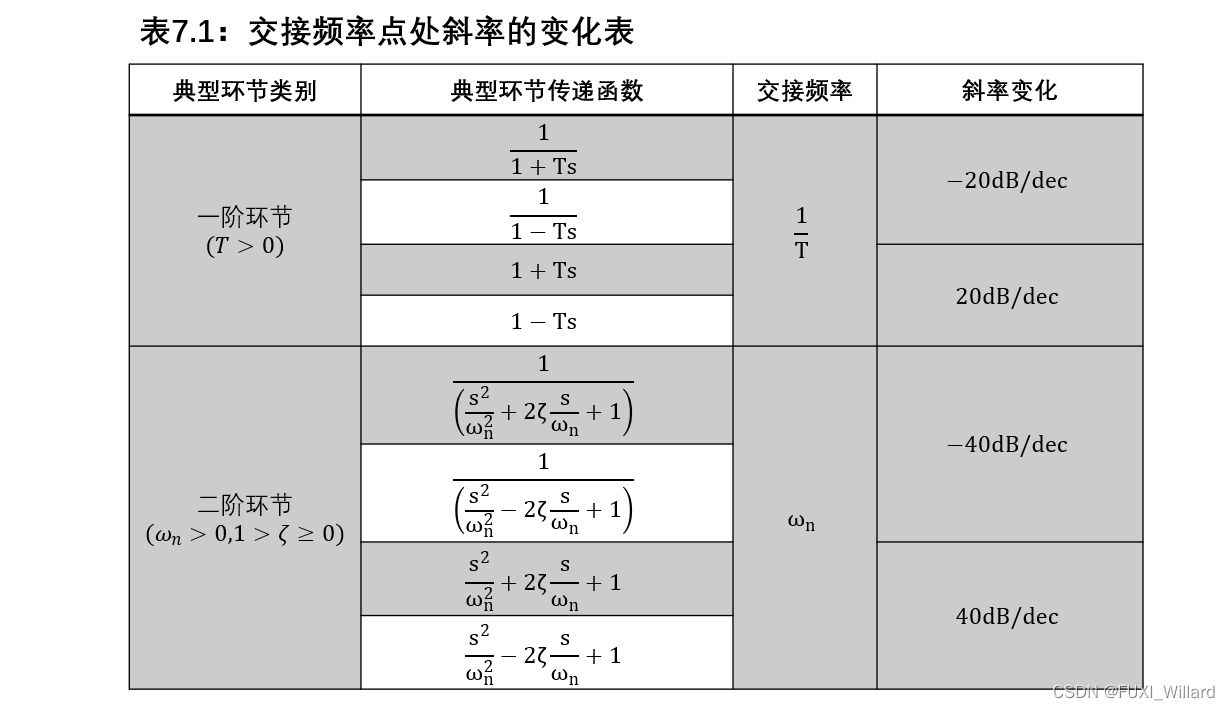
4. 作$\omega \ge {\omega }_{\min }$频段渐近特性线；在每个交接频率点处，斜率发生变化，变化规律取决于该交接频率对应的典型环节的种类，当系统的多个环节具有相同交接频率时，该交接频率点处斜率的变化应为各个环节对应的斜率变化值的代数和；

交接频率点处斜率的变化表：

1.3.5 延迟环节和延迟系统

输出量经恒定延时后不失真地复现输入量变化的环节称为延迟环节；含有延迟环节的系统称为延迟系统；

延迟环节的输入输出时域表达式为：
$$c(t)=1(t-\tau )r(t-\tau )$$
其中：$\tau$为延迟时间；

延迟环节的传递函数为：
$$G(s)=\frac{C(s)}{R(s)}={\mathrm{e}}^{-\tau s}$$
延迟环节的频率特性为：
$$G(j\omega )={\mathrm{e}}^{-\mathrm{j}\tau \omega }=1\cdot \angle (-57.3\tau \omega )$$

1.4 开环和闭环频率特性的性能分析

1.4.1 开环对数频率特性与时域响应的关系

1. 低频段分析。

   • 低频段：指$\mathrm{L}(\omega )=20\lg |G(\mathrm{j}\omega )|$的渐近线在第一个转折频率前的频段，这一频段的特性完全由积分环节和开环放大倍数决定；

   • 低频对数幅频特性为：
     $$L_d(\omega )=20\lg K-20\nu \lg \omega$$
     其中：$K$为开环放大倍数，$\nu$为开环传递函数中积分环节个数；

   • 低频段的频率特性决定系统的稳态性能；

2. 中频段分析。

   • 中频段：指开环对数幅频特性曲线在开环截止频率${\omega }_c$附近($0dB$附近)的区段，这一频段特性集中反映了闭环系统动态响应的平稳性和快速性；
   • 时域响应的动态特性主要取决于中频段的形状；
   • 反映中频段形状的三个参数：开环截止频率${\omega }_c$、中频段斜率、中频段宽度；
   • 开环对数幅频特性中频段斜率最好为$-20dB/dec$，且希望长度尽可能长，以确保系统有足够的相角裕度；当中频段的斜率为$-40dB/dec$时，中频段占据的频率范围不宜过长，否则相角裕度很小；若中频段斜率更小，系统则难以稳定；
   • 截止频率${\omega }_c$越高，系统复现信号能力越强，系统快速性越好；

3. 高频段分析。

   • 高频段：指开环对数幅频特性曲线在中频段以后的频段，高频段的形状主要影响时域响应的起始段；
   • 进行系统分析时，可将高频段进行近似处理，即用一个小惯性环节来等效多个小惯性环节，等效的小惯性环节的时间常数等于被替代的多个小惯性环节的时间常数之和；
   • 系统开环对数幅频特性在高频段的幅值，直接反映系统对高频干扰信号的抑制能力；高频部分的幅值越低，系统的抗干扰能力越强；

4. 良好系统的各频段形状。

   • 低频段要有一定的高度和斜率；
   • 中频段斜率最好为$-20dB/dec$，且具有足够的宽度；
   • 高频段采用迅速衰减的特性，以抑制不必要的高频干扰；

1.4.2 开环频率特性与时域响应的关系

典型二阶系统的频域指标和时域指标相互转换公式：
$$\begin{array}{rl}& {\omega }_c=\sqrt{\sqrt{1+4{\zeta }^4}-2{\zeta }^2}{\omega }_n，\gamma ({\omega }_c)=\arctan \frac{2\zeta }{\sqrt{\sqrt{1+4{\zeta }^4}-2{\zeta }^2}}\end{array}$$
高阶系统的频域指标和时域指标相互转换公式：
$$\begin{array}{rl}& {\sigma }_p=0.16+0.4\left(\frac{1}{\sin \gamma }-1\right)，35°\le \gamma \le 90°\\ & \\ & t_s=\frac{\pi }{{\omega }_c}\left[2+1.5\left(\frac{1}{\sin \gamma }-1\right)+2.5{\left(\frac{1}{\sin \gamma }-1\right)}^2\right]\end{array}$$

1.4.3 闭环频率特性与时域响应的关系

典型二阶系统闭环传递函数为：
$$\Phi (s)=\frac{{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}$$
可得系统闭环频率特性为：
$$\Phi (\mathrm{j}\omega )=\frac{{\omega }_n^2}{(\mathrm{j}\omega {)}^2+\mathrm{j}2\zeta {\omega }_n\omega +{\omega }_n^2}$$
系统闭环幅频特性为：
$$M(\omega )=\frac{{\omega }_n^2}{\sqrt{({\omega }_n^2-{\omega }^2{)}^2+(2\zeta {\omega }_n\omega {)}^2}}$$
系统闭环相频特性为：
$$\phi (\omega )=-\arctan \frac{2\zeta {\omega }_n\omega }{{\omega }_n^2-{\omega }^2}$$
二阶系统的谐振峰值$M_r$与时域超调量${\sigma }_p$间的关系为：
$${\sigma }_p={\mathrm{e}}^{-\zeta \pi /\sqrt{1-{\zeta }^2}}\times 100\%，M_r=\frac{1}{2\zeta \sqrt{1-{\zeta }^2}}$$

• 谐振峰值$M_r$仅与阻尼比$\zeta$有关，超调量${\sigma }_p$亦仅取决于阻尼比$\zeta$；

• $\zeta$越小，$M_r$增加得越快，超调量${\sigma }_p$亦很大，超过$40\%$，此时系统一般不符合瞬态响应指标要求；

• 当$0.4<\zeta <0.707$时，$M_r$与${\sigma }_p$变化趋势基本一致，此时谐振峰值$M_r=1.2～1.5$，超调量${\sigma }_p=20\%～30\%$,系统响应结果较为理想；

• 当$\zeta >0.707$时，无谐振峰值，$M_r$与$\sigma \%$对应关系不再存在，因此在设计中一般$\zeta$取值在$0.4～0.7$之间；

• 二阶系统谐振频率${\omega }_r$与峰值时间$t_p$间的关系：
  $$t_p{\omega }_r=\frac{\pi \sqrt{1-2{\zeta }^2}}{\sqrt{1-{\zeta }^2}}$$

• 当$\zeta$为常数时，谐振频率${\omega }_r$与峰值时间$t_p$成反比，${\omega }_r$值越大，$t_p$越小，系统时间响应越快；

• 二阶系统闭环截止频率${\omega }_b$与过渡过程时间$t_s$间的关系：
  $${\omega }_b{t}_s=\frac{3～4}{\zeta }\sqrt{1-2{\zeta }^2+\sqrt{2-4{\zeta }^2+4{\zeta }^4}}$$

• 当阻尼比$\zeta$给定后，闭环截止频率${\omega }_b$与过渡过程时间$t_s$成反比，${\omega }_b$越大，系统响应速度越快；