字节跳动后端工程师实习生笔试题-c++
字节跳动后端工程师实习生笔试题链接
笔试题
- 1. 最大映射
- 2. 木棒拼图
- 3. 魔法权值
- 4. 或与加
1. 最大映射
有 n 个字符串,每个字符串都是由 A-J 的大写字符构成。现在你将每个字符映射为一个 0-9 的数字,不同字符映射为不同的数字。这样每个字符串就可以看做一个整数,唯一的要求是这些整数必须是正整数且它们的字符串不能有前导零。现在问你怎样映射字符才能使得这些字符串表示的整数之和最大?
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 32M,其他语言64M
输入描述:
每组测试用例仅包含一组数据,每组数据第一行为一个正整数 n , 接下来有 n 行,每行一个长度不超过 12 且仅包含大写字母 A-J的字符串。 n 不大于 50,且至少存在一个字符不是任何字符串的首字母。
输出描述:
输出一个数,表示最大和是多少。
示例1
输入例子:
2
ABC
BCA
输出例子:
1875
有时间找了一份笔试题做做,结果还是一言难尽,这些编程题的题目都需要深刻的去理解,不然忽略一小段话,一个小细节,都会让自己在电脑面前怀疑半天,刷了一些算法题,能力提升没提升不知道,反正心里承受能力是一定会提升的,行了,下面看看这份笔试题。
-
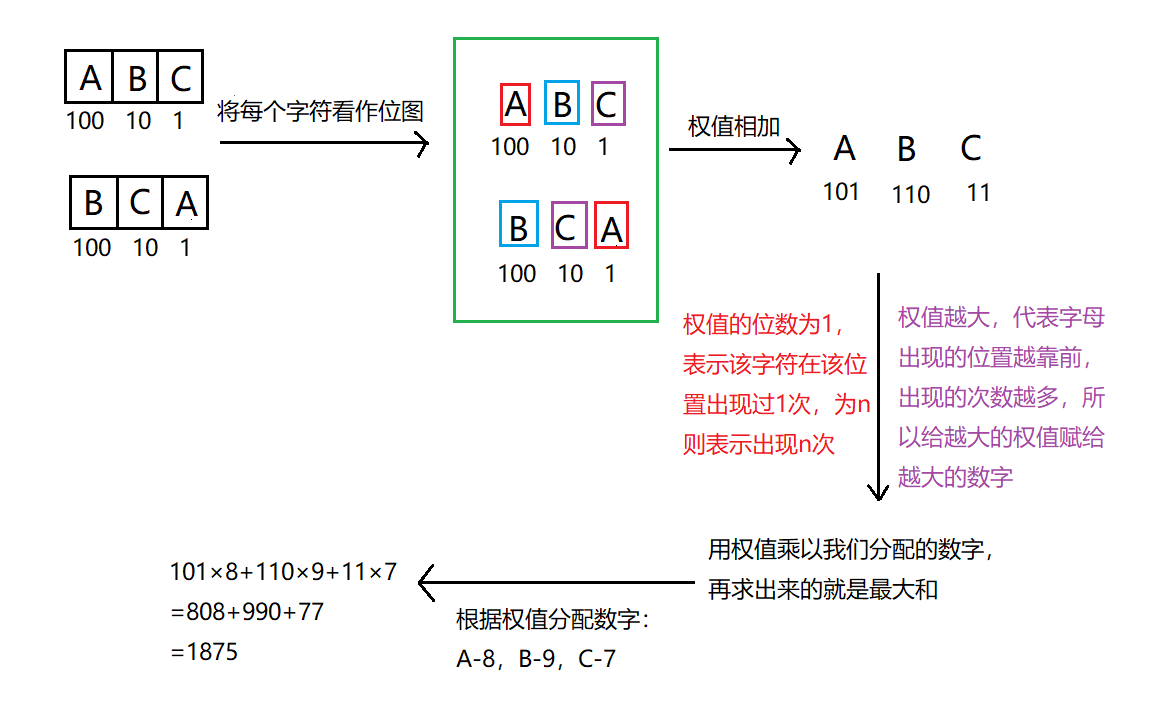
题目解析:这道题的输入是n条字符串,字符串为A-J,映射为0-9,不同字符映射为不同的数字,如示例1:可以将ABC映射为987,则BCA就为879,和为1866;或者将ABC映射为897,则BCA就为978,和为1875;或者将ABC映射为789,则BCA就为897,和为1696,最大值为1875,所以输出最大值即可。还有最重要的一个条件:且它们的字符串不能有前导零, 意思就是字符串的首字母不能赋值为0,输入描述中也说过,至少存在一个字符不是任何字符串的首字母,题目大致意思也就这些。
-
解题思路:我当时看完题目一想,好吧不会,我承认我是菜狗。不会怎么办呢?百度呗,看了某位佬的思路和解法,这位佬将这道题也只写了一半,没有将字符串不能有前导零考虑在内,但有了思路,接下来就自己思考思考吧,不然就会变得越来越菜。大致思路,要求得最大和与字符出现的位置和次数有关,对于某一字符串来说,越排在前面的字符,它所占的权值就越大,所以可以对字符串的位置设置权值,如1,10,100,1000…等,权重有那么多种,为什么要设置为1,10,100,1000…这种,这种设置对于后续来说方便计算,结合下图来看:由下图知,最后我们只需将权值与分配的数字相乘就可以得到最大和。
-
代码如下:
#include <iostream>
#include <string>
#include <algorithm>
#include <cmath>
using namespace std;
int main()
{
int n;
cin >> n;
string str;
long long MAX = 0, A[10] = {0};
while (n--)
{
cin >> str;
for (int i = str.length() - 1; i >= 0; i--)
{
A[str[i] - 'A'] += pow(10, str.length() - i - 1);
}
}
sort(A, A + 10);
for (int i = 0; i <= 9; i++)
{
MAX += (A[i] * i);
}
cout << MAX;
}
上述代码没有考虑到它们的字符串不能有前导零这一条件,所以20个样例过了17个,然后思考怎么设置零不能出现在最前面的位置,试着思考思考。用set?map?unordered_map?用这类容器将出现的首字符记录下来,解决应该可以解决,我没想到,因为还需要对权重进行排序,而上述容器是不能排序的,又或者说他们是已经排好序的,所以我直接再用一个数组hash来记录首字母的出现情况,给权重排序时顺便给hash也排序,因为需要对他们一一对应,完整代码如下:
#include <iostream>
#include <vector>
#include <string>
#include <math.h>
#include <algorithm>
#include <set>
using namespace std;
int main()
{
long long ret = 0;
int n = 0;
cin >> n;
string str;
long long weight[10] = { 0 }; // weight用来记录权重
int ch[10] = { 0 }, hash[10] = { 0 }; // hash用来记录哪个字母是首字母,ch用来记录数字分配给哪个字母,hash和ch搭配起来使用
for (int i = 0; i < 10; ++i)
ch[i] = i; // 首先就将0给A,1给B...i表示哪个数字,ch[i]表示哪个字母
for (int i = 0; i < n; ++i)
{
cin >> str;
int size = str.size();
for (int i = size - 1; i >= 0; --i)
{
weight[str[i] - 'A'] += pow(10, size - i - 1);
if (i == 0)
hash[str[i] - 'A'] = 1; // 记录哪个字母是在首位出现的
}
}
// 对权值和对应的字母排序
for (int i = 0; i < 10; ++i)
{
for (int j = i + 1; j < 10; ++j)
{
if (weight[i] > weight[j])
{
swap(weight[i], weight[j]);
swap(ch[i], ch[j]);
}
}
}
int i = 1;
while (hash[ch[0]]) // hash[ch[0]]表示分配0的字母是否在字符串的首位出现
{
swap(weight[i], weight[0]);
swap(ch[i], ch[0]);
++i;
}
for (int i = 0; i < 10; ++i)
ret += i * weight[i];
cout << ret;
return 0;
}
当然还有别的解法,欢迎各位佬分享自己的心得,可以互相交流交流。
2. 木棒拼图
有一个由很多木棒构成的集合,每个木棒有对应的长度,请问能否用集合中的这些木棒以某个顺序首尾相连构成一个面积大于 0 的简单多边形且所有木棒都要用上,简单多边形即不会自交的多边形。
初始集合是空的,有两种操作,要么给集合添加一个长度为 L 的木棒,要么删去集合中已经有的某个木棒。每次操作结束后你都需要告知是否能用集合中的这些木棒构成一个简单多边形。
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 32M,其他语言64M
输入描述:
每组测试用例仅包含一组数据,每组数据第一行为一个正整数 n 表示操作的数量(1 ≤ n ≤ 50000)
,接下来有n行,每行第一个整数为操作类型 i (i ∈ {1,2}),第二个整数为一个长度 L(1 ≤ L
≤1,000,000,000)。如果 i=1 代表在集合内插入一个长度为 L 的木棒,如果 i=2 代表删去在集合内的一根长度为
L的木棒。输入数据保证删除时集合中必定存在长度为 L 的木棒,且任意操作后集合都是非空的。
输出描述:
对于每一次操作结束有一次输出,如果集合内的木棒可以构成简单多边形,输出 “Yes” ,否则输出 “No”。
示例1
输入例子:
5
1 1
1 1
1 1
2 1
1 2
输出例子:
No
No
Yes
No
No
- 题目解析:这道题的意思简单明了,有一个集合,这个集合存放正整数,这些正整数代表着多边形的边,可以向这个集合插入或者删除数据,如果这些边可以组成一个多边形,那么输出Yes,否则输出No,每次插入或者删除都需要输出,并且将要删除的边一定是在这个集合中的。
- 解题思路:第一次读完题后,完全没思路,这根本和leetcode中的算法题不一样,而且经过第一道题的铺垫,觉得这道题应该很高大上,因为与多边形有关,所以往难的方向猜,一定有某位数学家得出通过边的长短来计算能否构成多边形的公式,脑海中出现一位数学家坐在木质凳子上用一根笔在纸上留下绚丽多彩的一笔,但我肯定不知道这个公式,以为这道题又要寄了;为了这道题不寄,我明白我必须要做出一些行动来尝试尝试,我就往简单的方向猜,提到能否构成多边形,通常做的最多的就是判断三条边能否构成一个三角形,而想要三条边构成一个三角形,那么只需要三条边中的最长边小于另外两边之和,那么判断构成多边形的条件是不是只要最长的边小于其余的边之和即可? 我不知道,所以就尝试尝试呗。分析,其余边之和大于最长边的长度,那么其余边就可以将最长边给围起来,其余边之和比最长边越长,那么所围的面积就越大,其余边之和比最长边小,那么就围不在一起,就不能构成多边形。
- 代码如下,(代码有些丑陋,有优化的地方欢迎指出。曾经看到一个视频,视频中的人说,代码对于程序员来说是隐私,就好比是我们穿着内裤的颜色,代码写的差我认,但你不能看我“内裤”的颜色)
#include <iostream>
#include <map>
using namespace std;
void print(map<long long, int> &hash, long long &sum, int &size)
{
if (size < 3)
cout << "No" << endl;
else if (size >= 3)
{
int max_len = (--hash.end())->first; // 每次取出最长的边
int tmp = sum - max_len;
if (tmp > max_len)
cout << "Yes" << endl;
else
cout << "No" << endl;
}
}
int main()
{
int n = 0, size = 0;
map<long long, int> hash;
long long sum = 0;
cin >> n;
while (n--)
{
int op = 0, len = 0;
cin >> op >> len;
if (op == 1)
{
sum += len;
hash[len]++;
++size;
print(hash, sum, size);
}
else if (op == 2)
{
sum -= len;
hash[len]--;
if (hash[len] == 0)
hash.erase(len);
--size;
print(hash, sum, size);
}
}
return 0;
}
3. 魔法权值
给出 n 个字符串,对于每个 n 个排列 p,按排列给出的顺序(p[0] , p[1] … p[n-1])依次连接这 n 个字符串都能得到一个长度为这些字符串长度之和的字符串。所以按照这个方法一共可以生成 n! 个字符串。
一个字符串的权值等于把这个字符串循环左移 i 次后得到的字符串仍和原字符串全等的数量,i 的取值为 [1 , 字符串长度]。求这些字符串最后生成的 n! 个字符串中权值为 K 的有多少个。
注:定义把一个串循环左移 1 次等价于把这个串的第一个字符移动到最后一个字符的后面。
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 32M,其他语言64M
输入描述:
每组测试用例仅包含一组数据,每组数据第一行为两个正整数 n, K , n 的大小不超过 8 , K 不超过 200。接下来有 n行,每行一个长度不超过 20 且仅包含大写字母的字符串。
输出描述:
输出一个整数代表权值为 K 的字符串数量。
示例1
输入例子:
3 2
AB
RAAB
RA
输出例子:3
- 题目解析:这道题的意思还是有些难理解的,接下来分析一下,有n个字符串,这n个字符串可以通过不同的排列组成新的字符串,会有n*(n-1)*(n-2)*…*2*1个新的字符串,然后就是这个权值,将组成新的字符串向左移动 i 位 (i 的取值为 [1 , 字符串长度]),如果移动后的字符串等于移动前的字符串,那么这个字符串的权值就+1,输出组合后权值为 K 的新字符串的个数,题目的是、大致意思就这些。
- 解题思路:要组成新的字符串,全排列的算法就可以算出(知道的就用递归做,不知道的建议先学习一下全排列);组成新的字符串后,那就开始向左移动,要是单纯的将新的字符串进行移动,那么太耗时了,所以不建议,有另一个思路就是将新的字符串加等于本身的字符串,然后只需要将寻找的区间往后滑动即可,不善于表达,如下图所示:
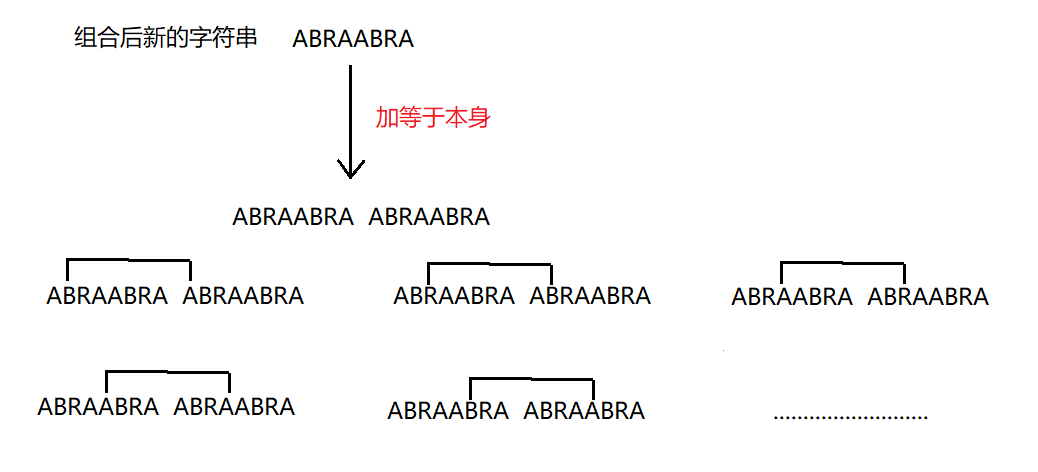
- 代码如下:
#include <iostream>
#include <vector>
#include <string>
using namespace std;
int n = 0, k = 0, ret = 0;
bool check[10]; // 检查该数据的位置是否使用,true表示使用,false表示未使用
vector<string> combstr; // 组合后的字符串数组
vector<string> path; // 已选取的字符串
// 全排列算法
void dfs(vector<string>& nums)
{
if (path.size() == n)
{
string comb;
for (auto& str : path)
comb += str;
combstr.push_back(comb);
// 顺便处理combstr
combstr[combstr.size() - 1] += combstr[combstr.size() - 1];
return;
}
for (int i = 0; i < n; ++i)
{
if (!check[i])
{
check[i] = true;
path.push_back(nums[i]); // 选取该位置的字符串
dfs(nums);
check[i] = false;
path.pop_back();
}
}
}
int main()
{
cin >> n >> k;
vector<string> nums(n);
int len = 0;
for (int i = 0; i < n; ++i)
{
cin >> nums[i];
len += nums[i].size();
}
dfs(nums);
for (int i = 0; i < combstr.size(); ++i)
{
string prostr = combstr[i].substr(0, len); // 原始字符串
int count = 0;
for (int j = 1; j <= len; ++j) // 取值为[1, 字符串长度]
{
string tmp = combstr[i].substr(j, len);
if (prostr == tmp)
++count;
}
if (count == k)
++ret;
}
cout << ret << endl;
// 检查组合后的字符串是否正确
//for (int i = 0; i < combstr.size(); ++i)
// cout << combstr[i] << endl;
return 0;
}
4. 或与加
给定 x, k ,求满足 x + y = x | y 的第 k 小的正整数 y 。 | 是二进制的或(or)运算,例如 3 | 5 = 7。
比如当 x=5,k=1时返回 2,因为5+1=6 不等于 5|1=5,而 5+2=7 等于 5 | 2 = 7。
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 32M,其他语言64M
输入描述:
每组测试用例仅包含一组数据,每组数据为两个正整数 x , k。 满足 0 < x , k ≤ 2,000,000,000。
输出描述:
输出一个数y。
示例1
输入例子:
5 1
输出例子:
2
- 题目解析:这道题的题意清晰明了,但是做法肯定不是从1开始暴力求解,这样耗时非常高,所以用别的方法解决;题目中出现与或等逻辑算术,那么就要向二进制的方向思考,1 | 0 = 1, 1 | 1 = 1,所以只要找x的二进制为0的位置,在二进制为0的位置加1就不会向前进位,这样x + y = x | y;还有一个问题是找第k个,假设x为10,二进制为1010,我们可以在0的位置插入1,插入1后如:0001,0100,0101这3种,只看x为0的位置,那么上述是0的位置为1,10,11,如果k=1,那么y=0001;如果k=2,那么y=0100;如果k=3,那么y=0101;如果k=4,那么y=10000…所以我们可以将k的二进制位放在x二进制为0的位置上,其余位置附0即可,如下图所示:

2. 代码如下:
#include <iostream>
#include <vector>
using namespace std;
int main()
{
long long x = 0, k = 0;
cin >> x >> k;
vector<int> binary; // 存放k二进制位的数组
while (k)
{
binary.push_back(k % 2);
k /= 2;
}
long long tmp = 1;
long long y = 0;
int count = 0;
while (count < binary.size())
{
while (x % 2)
{
x /= 2;
tmp *= 2;
}
if (binary[count] == 1)
{
y += tmp;
}
x /= 2;
tmp *= 2;
++count;
}
cout << y << endl;
return 0;
}
