动态规划

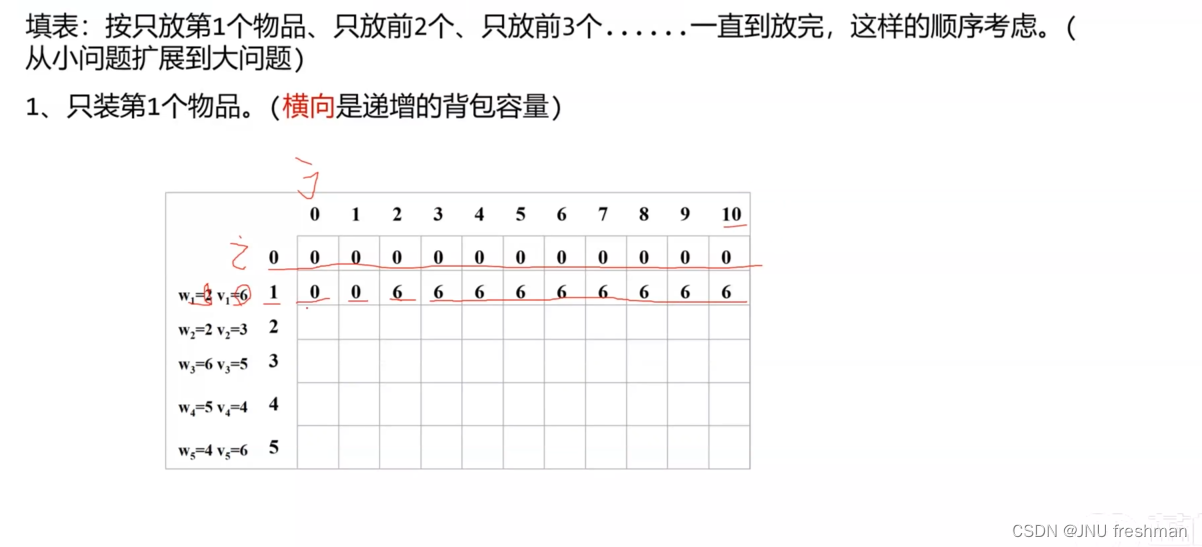
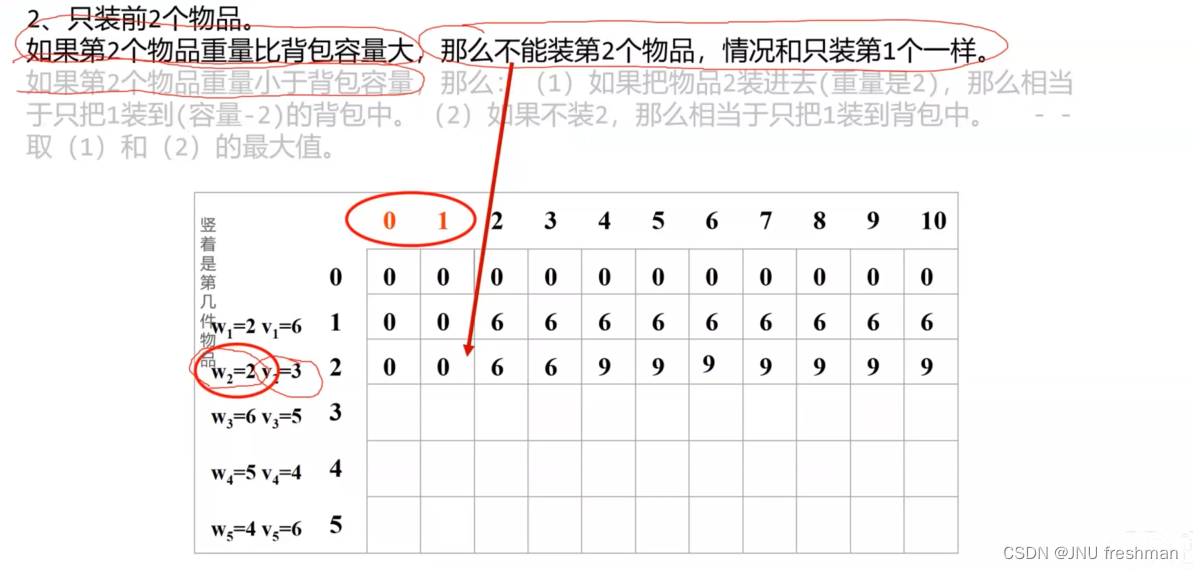
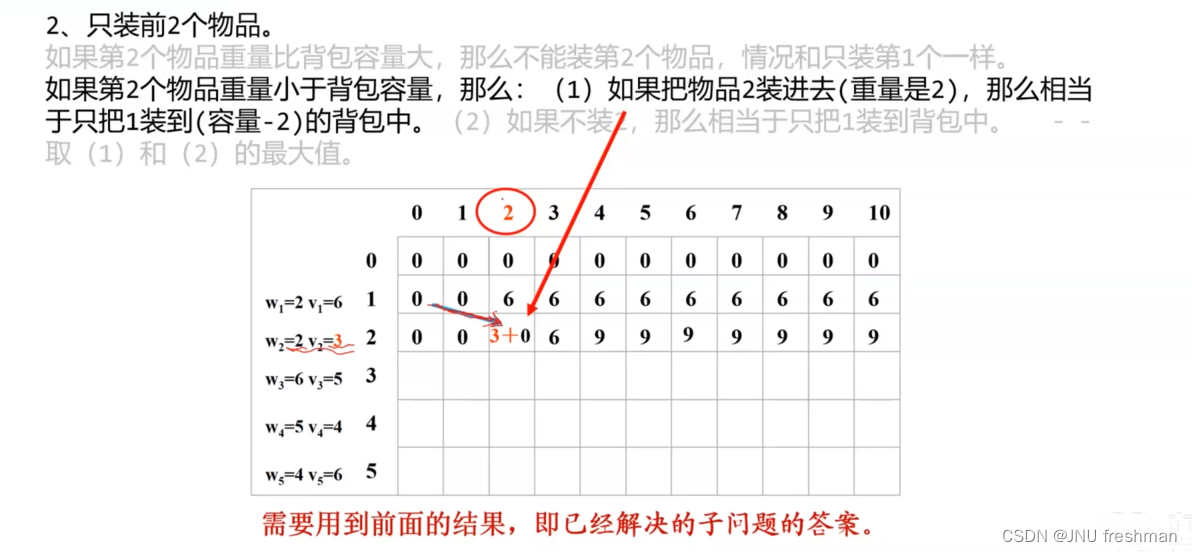
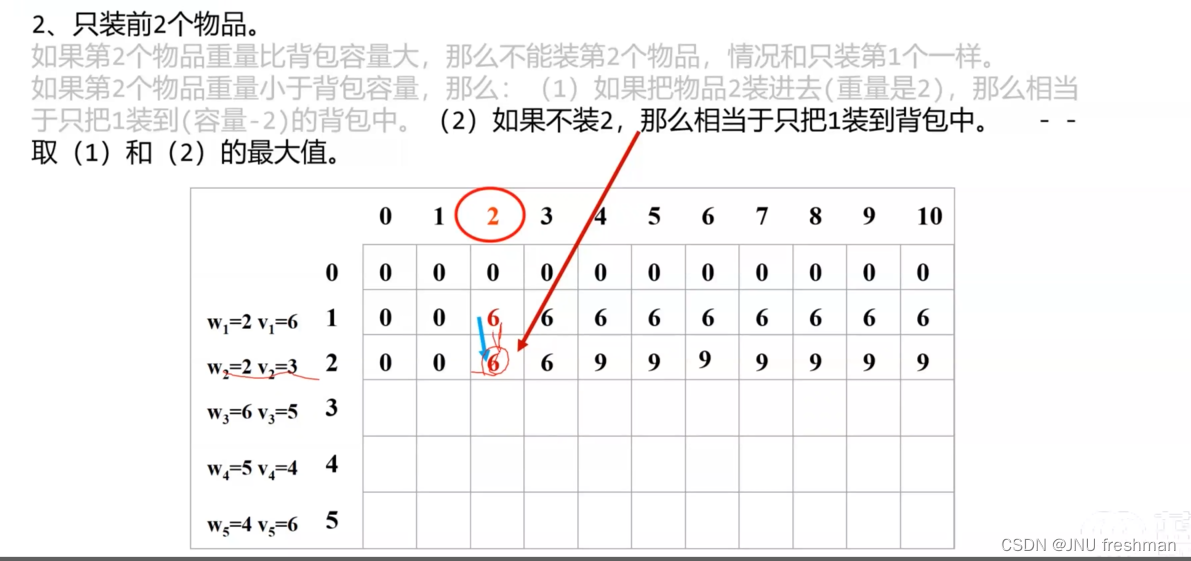
01背包

由于不能拆开，那就是DP 问题，如果能拆开，那就是贪心问题

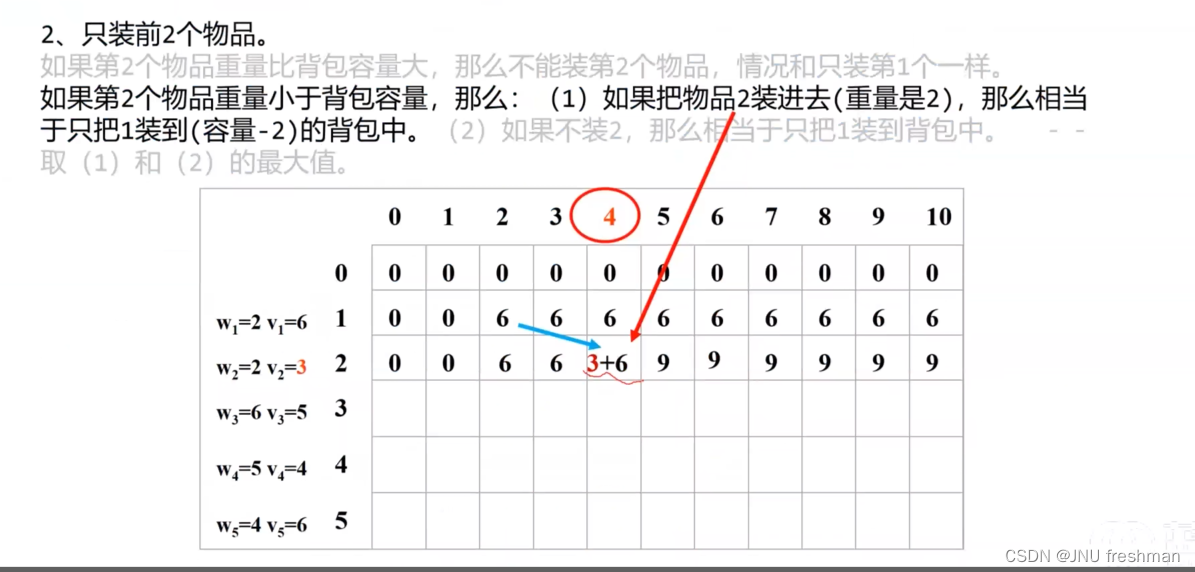
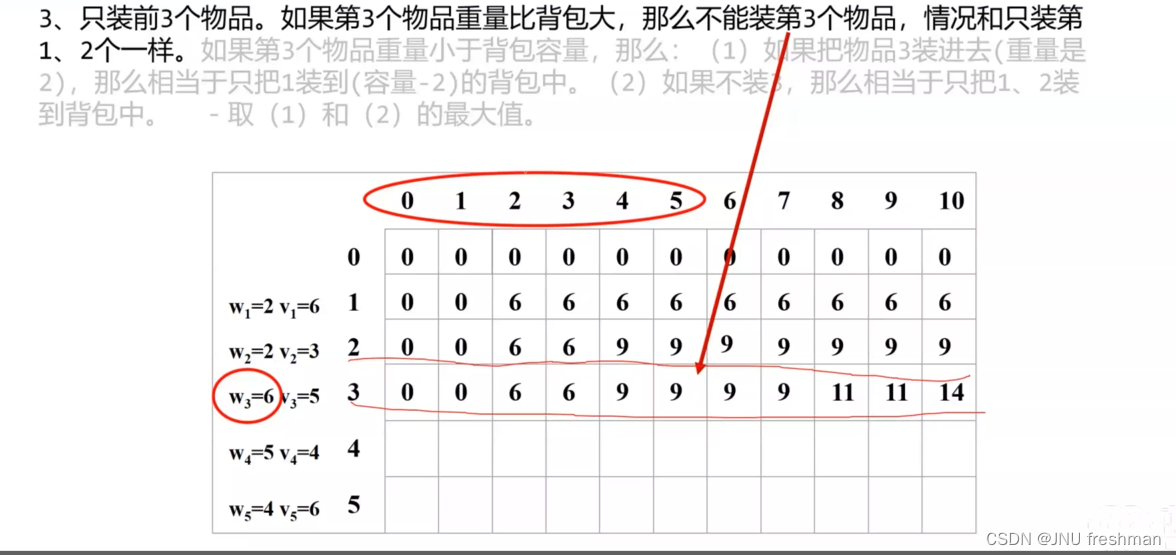
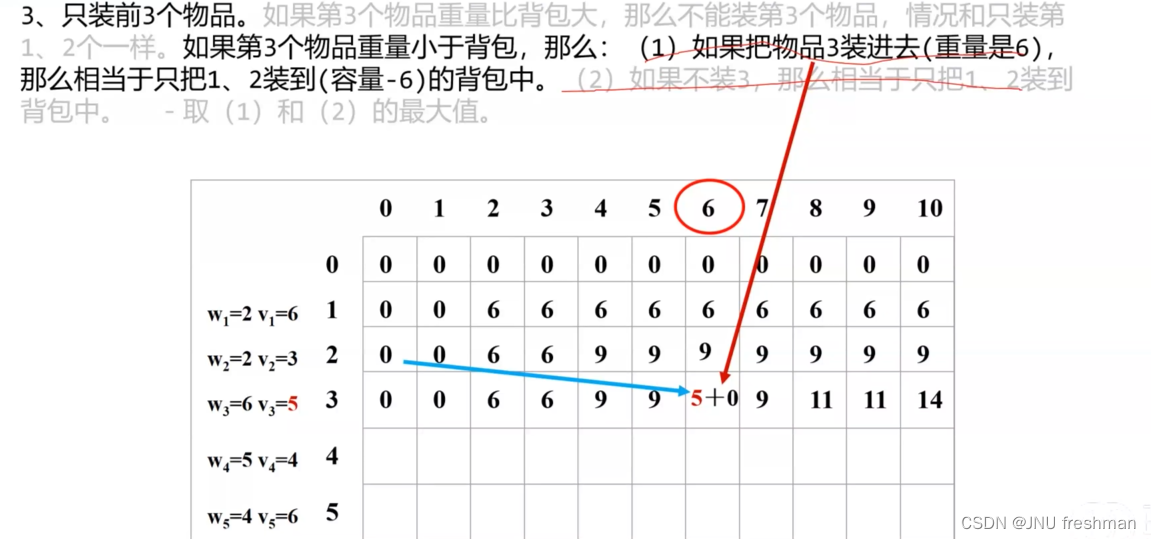
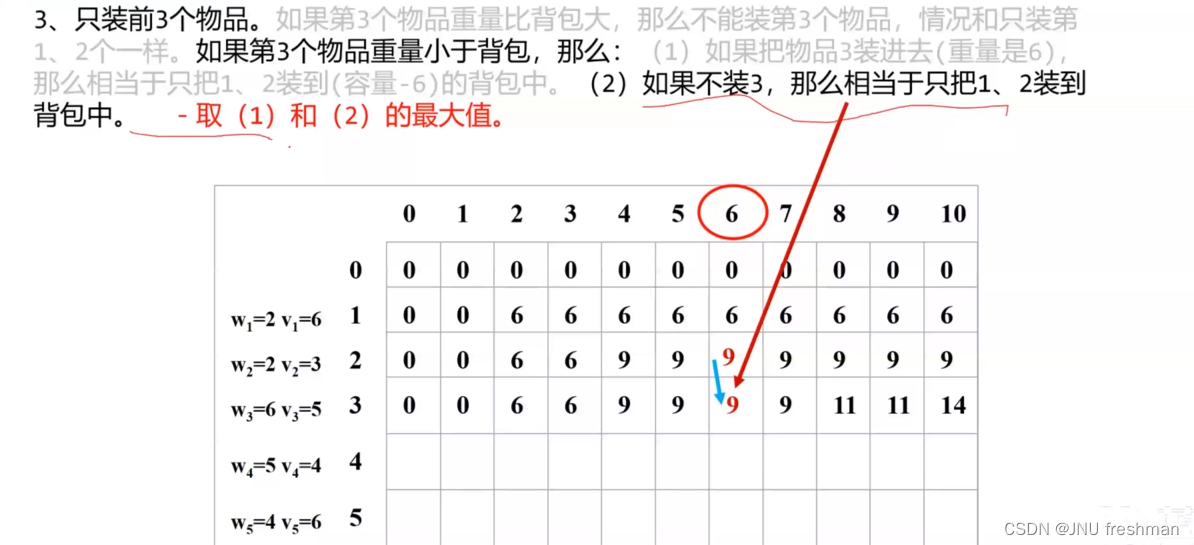
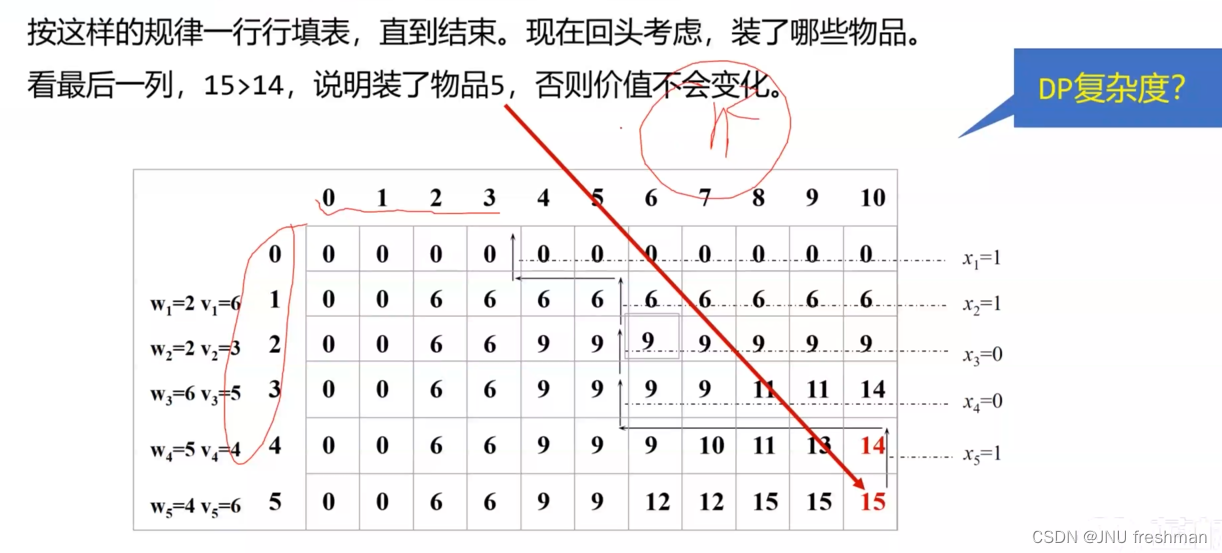
小练一下

import os
import sys

# 请在此输入您的代码

N,V = map(int,input().split())

w = []
v = []
w.append(0)
v.append(0)

for i in range(N):
  a,b = map(int,input().split())
  w.append(a)
  v.append(b)

dp = [[0]*(V+1) for _ in range(N+1)]

for i in range(1,N+1):# 取出第i 个物品
  for j in range(V+1):

    if j-w[i]<0:
      dp[i][j]=dp[i-1][j]
    else:
      dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])

print(dp[N][V])

• 可以对空间进行优化：只用添加两个变量来存储new,old 就是利用滚动数组，两个数组即可解决

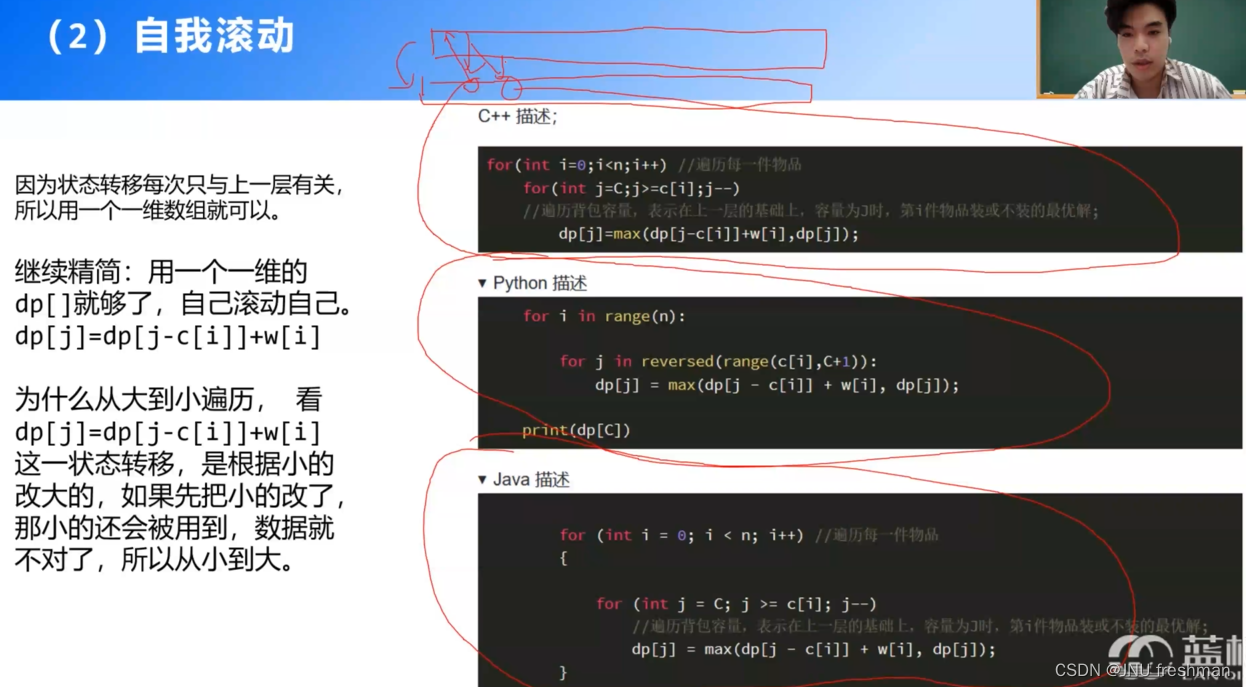
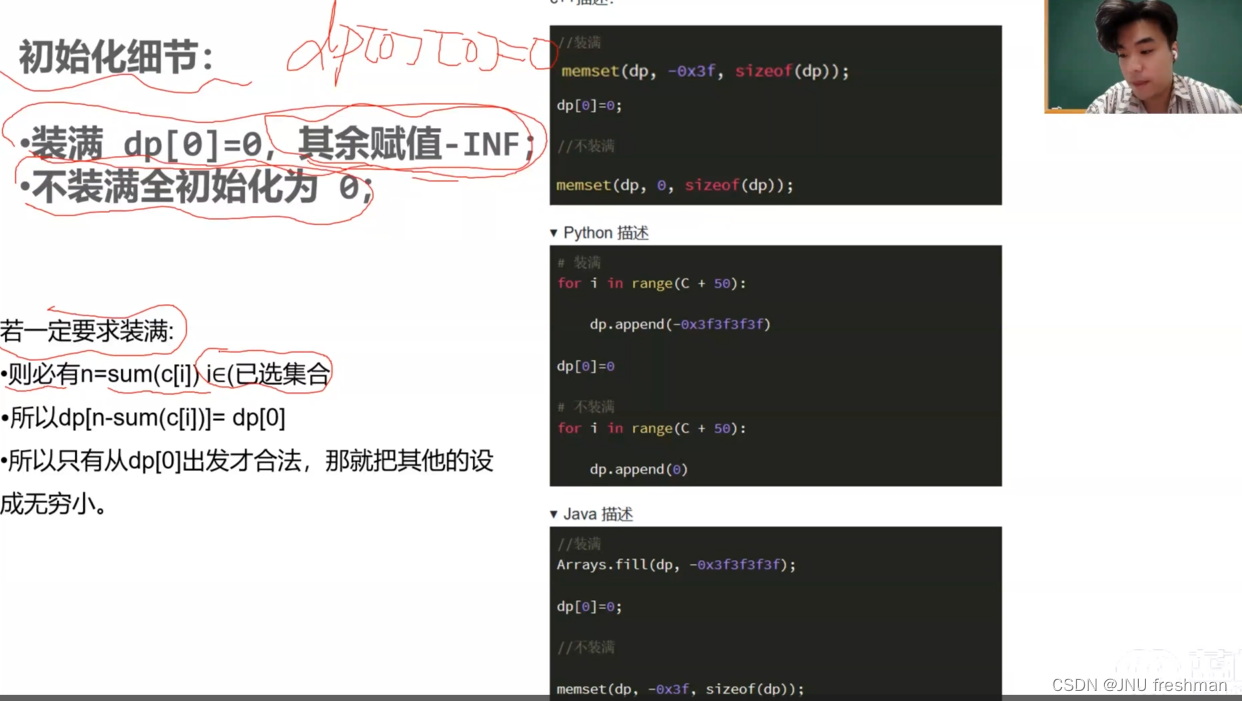
import os
import sys

V = int(input())#####箱子容量
n = int(input())####物品数量
l = [0]####各自体积
for i in range(n):####输入体积
  l.append(int(input()))
dp = [[0 for j in range(V+1)]for i in range(n+1)]

for i in range(1,n+1):###
  for j in range(1,V+1):####
    if j < l[i]:####
      dp[i][j] = dp[i-1][j]
    else:
      dp[i][j]=max(dp[i-1][j],dp[i-1][j-l[i]]+l[i])###
print(V-dp[n][V])

同样的思路：还是用二维数组存储，dp[i][j]表示 前i 个物体在空间j 的情况下，所能放的空间的大小

网格图上的DP