算法刷题总结 (二) 回溯与深广搜算法
算法总结2 回溯与深广搜算法
- 一、理解回溯算法
- 1.1、回溯的概念
- 1.2、回溯法的效率
- 1.3、回溯法问题分类
- 1.4、回溯法的做题步骤
- 二、经典问题
- 2.1、组合问题
- 2.1.1、77. 组合 - 值不重复
- 2.1.2、216.组合总和III - 值不重复且等于目标值
- 2.1.3、17. 电话号码的字母组合 - 双层回溯
- 2.1.4、39. 组合总和 - 可复选同一值
- 2.1.5、40.组合总和II - 不可复选同一值,但有重复元素
- 2.1.6、练习
- 22. 括号生成
- 2.2、分割问题
- 2.2.1、131. 分割回文串 - 回溯附加条件
- 2.2.2、93.复原IP地址 - 回溯附加条件
- 2.3、子集问题
- 2.3.1、78. 子集 - 整棵遍历数
- 2.3.2、90. 子集 II - 乱序+重复元素+去重复值
- 2.4、排列问题
- 2.4.1、46.全排列
- 2.4.2、47.全排列 II
- 2.5、应用型类似问题
- 2.5.1、491.递增子序列 (和子集问题很像)- 非排序+重复元素+去重
- 2.5.2、332.重新安排行程(和2.1.3、17. 电话号码的字母组合 很像)
- 2.6、棋盘问题
- 2.6.1、HJ43 迷宫问题
- 2.6.2、51. N 皇后
- 2.6.3、37. 解数独
- 三、深搜DFS与广搜BFS
- 3.1、岛屿问题
- 200. 岛屿数量
- 1. 深度优先搜索DFS
- 2. 广度优先搜索 BFS
- 1254. 统计封闭岛屿的数目
- 1.深度优先搜索DFS
- 2.广度优先搜索
- 3.深度优先/广度优先 去除边界连通面积
- 1020.飞地的数量
- 695. 岛屿的最大面积
- 1.深度优先搜索DFS
- 2.广度优先搜索 BFS
- 1905. 统计子岛屿
- 130. 被围绕的区域
- 417. 太平洋大西洋水流问题
- 3.2、集合划分问题(等用于回溯的问题)
- 698. 划分为k个相等的子集
- 473. 火柴拼正方形
- 2305. 公平分发饼干
- 1723. 完成所有工作的最短时间
- 3.3、其他问题
- 547. 省份数量
- 参考

一、理解回溯算法
回溯与深广搜有相似的做法和理解,所以把他们放在同一个文章之中,文章看似篇幅很长,实际上,题目都是相似的,顺着章节来可以很快的掌握这个算法内容,以后碰到这样的相似题目,会很快想出思路。
1.1、回溯的概念
回溯是递归的纵横拓展,主要是递归(纵)+局部暴力枚举(横)。所以可以从递归和暴力两个方面来拆解回溯问题。
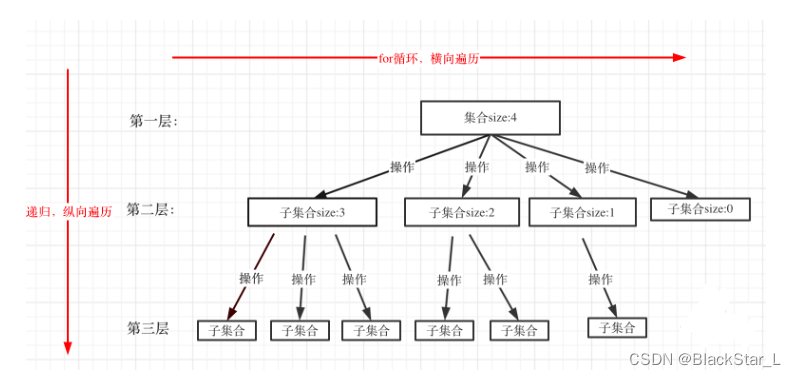
由上图可知,回溯法的所有问题都可以抽象为树形结构,集合的大小构成了树的宽度,递归深度构成了树的深度(N叉树)。因为递归有终止条件,所以树的高度会有限,同时递归的最终结果会呈现在叶子节点上。
1.2、回溯法的效率
从上一节的概念可知,回溯=递归+暴力搜索,所以它并不是一个特别高效的算法,即便再做一些剪枝优化下,依旧改变不了它的整体就是穷举的特性。
但即便这个算法效率不高,它的使用依旧很广泛,因为很多问题除了穷举,实在就是没有别的解决办法了,具体可以看看下一章的例题感受下。
1.3、回溯法问题分类
回溯法主要解决以下五种问题:
| 问题 | 描述 |
|---|---|
| 组合问题 | N个数里面按一定规则找出k个数的集合 |
| 切割问题 | 一个字符串按一定规则有几种切割方式 |
| 子集问题 | 一个N个数的集合里有多少符合条件的子集 |
| 排列问题 | N个数按一定规则全排列,有几种排列方式 |
| 棋盘问题 | N皇后,解数独,迷宫等等 |
1.4、回溯法的做题步骤
回溯法三部曲:
- 回溯函数的模板,返回值以及参数
这里回溯函数起名为backtracking,回溯算法中函数返回值一般为空。
对于参数的话,很难提前确定下来,一般是先写逻辑,然后需要什么参数,就填什么参数。
def backtracking(参数):
- 回溯函数终止条件
什么时候达到了终止条件,树中就可以看出,一般来说搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。
if 终止条件:
保存结果
return
- 回溯搜索的遍历过程
# 横向遍历。一个节点有多少个孩子就执行多少次
for i in [本层集合中的元素(树中及节点孩子的数量就是集合的大小)]:
处理节点
# 纵向遍历,自己调用自己实现递归
backtracking(路径,选择列表)
回溯,撤销处理结果
总结:
def backtracking(参数):
if 终止条件:
存放结果
return
for i in [本层集合中的元素(树中及节点孩子的数量就是集合的大小)]:
处理节点
# 纵向遍历,自己调用自己实现递归
backtracking(路径,选择列表)
回溯,撤销处理结果
二、经典问题
2.1、组合问题

2.1.1、77. 组合 - 值不重复
力扣题目链接
1.使用函数:
itertools库下的combinations组合函数,与之对应的是permutations排列函数。
from itertools import combinations
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
l = [i+1 for i in range(n)]
res = combinations(l, k)
return list(res)
2.回溯法:
从题目可以知道,k=2两层循环解决,k=3三层循环,但是题目的k是变动的,也就是for循环的层数是需要是变动的,那么回溯法就用递归来解决层数嵌套,每递归一次就是一层for循环,一个简单的过程如下:
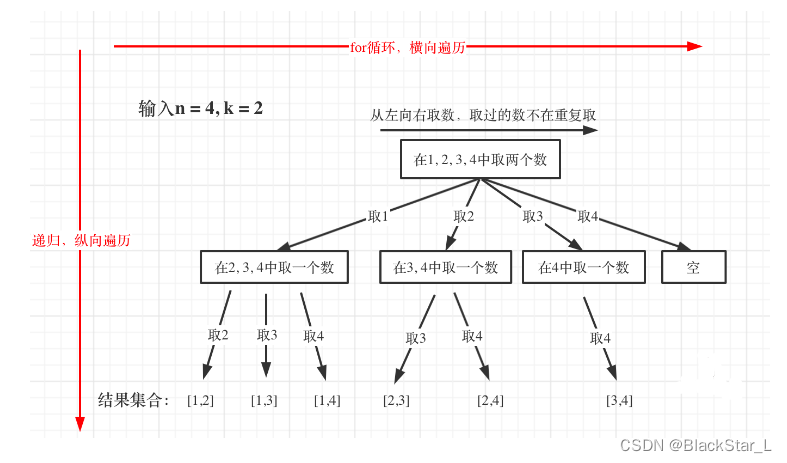
n相当于树的宽度,k相当于树深度的
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
# 存放符合条件结果的集合
result = []
# 存放符合条件单一结果
path = []
# startIndex来记录下一层递归,搜索的起始位置
def backtracking(n, k, startIndex):
if len(path)==k:
# 这里注意要添加一个path的拷贝,直接append为原址
# path最后会被pop,结果为空值
result.append(path[:])
return
for i in range(startIndex, n+1):
path.append(i)
backtracking(n, k, i+1)
path.pop()
backtracking(n, k, 1)
return result
加上剪枝操作(当path为固定长度时):
如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了,那么就没有必要搜索了。那么后面这些部分可以剪掉,如下,只用更改循环的终止条件改变范围就行。
# 这里
# n - (k-len(path))+1恰好满足最后一个长度到结尾
# 再往右就不满足了
# n = 4, k = 2, 当len(path) = 1 时
# 4 - (2 - 1) +1 = 4,从startindex到4都是可以取的
endIndex = n - (k-len(path))+1
for i in range(startIndex, endIndex+1):
path.append(i)
backtracking(n, k, i+1)
path.pop()
当然,这个剪枝是针对,有固定长度k才可取。
综上为:
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
# 存放符合条件结果的集合
result = []
# 存放符合条件单一结果
path = []
# startIndex来记录下一层递归,搜索的起始位置
def backtracking(n, k, startIndex):
if len(path)==k:
result.append(path[:])
return
# n = 4, k = 2, 当len(path) = 1 时
# 4 - (2 - 1) +1 = 4,从startindex到4都是可以取的
endIndex = n - (k-len(path))+1
for i in range(startIndex, endIndex+1):
path.append(i)
backtracking(n, k, i+1)
path.pop()
backtracking(n, k, 1)
return result
2.1.2、216.组合总和III - 值不重复且等于目标值
力扣题目链接
1.使用函数:
from itertools import combinations
class Solution:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
res = []
l = combinations([i+1 for i in range(9)], k)
for i in list(l):
if sum(i)==n:
res.append(i)
return res
2.回溯搜索:
class Solution:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
res = []
path = []
def backtracking(ind):
if len(path)==k:
if sum(path)==n:
res.append(path[:])
return
# 剪枝1,同前面的原理
endindex = 9-(k-len(path))+1
for i in range(ind, endindex+1):
path.append(i)
# 剪枝2,和大了就不继续回溯,这个放前面,backtracking下第一行也行
if sum(path)<=n:
backtracking(i+1)
path.pop()
backtracking(1)
return res
加上两次剪枝:
class Solution:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
path = []
res = []
def backtracking(k, n, startIndex):
# 剪枝1,大于目标值,再遍历也没意义,直接去掉
if sum(path)>n:
return
if len(path)==k and sum(path)==n:
res.append(path[:])
return
# 剪枝2,需要搭配剪枝1,否则k-len(path)会为负数,循环次数反而会增加
endIndex = 9 - (k-len(path))+1
for i in range(startIndex, endIndex+1):
path.append(i)
backtracking(k, n, i+1)
path.pop()
backtracking(k, n, 1)
return res
本题与77.组合 加了元素总和的限制,同样的,把问题抽象为树形结构,按照回溯算法的步骤走,最后给出剪枝的优化。

2.1.3、17. 电话号码的字母组合 - 双层回溯
力扣题目链接
回溯法1,从digits的角度:
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
d = {'2':'abc', '3':'def', '4':'ghi', '5':'jkl', '6':'mno', '7':'pqrs','8':'tuv','9':'wxyz'}
# 存储根节点
path = []
# 存储最终结果
res = []
# 回溯数字
def backtracking(digits):
if len(digits)==0:
# 去除空值,非空则添加字符串
if path:
res.append(''.join(path[:]))
return
# 循环取一个数字对应的字母
for i in d[digits[0]]:
# 存一个该数字的字母
path.append(i)
# 去除第一个数字,后面的数字串
backtracking(digits[1:])
path.pop()
backtracking(digits)
return res
回溯法2:从index的角度:
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
alphas = {"2":"abc","3":"def","4":"ghi","5":"jkl","6":"mno","7":"pqrs",
"8":"tuv","9":"wxyz"}
path = []
res = []
def backtracking(ind):
if len(path)==len(digits):
if path:
res.append(''.join(path[:]))
return
for a in alphas[digits[ind]]:
path.append(a)
backtracking(ind+1)
path.pop()
backtracking(0)
return res
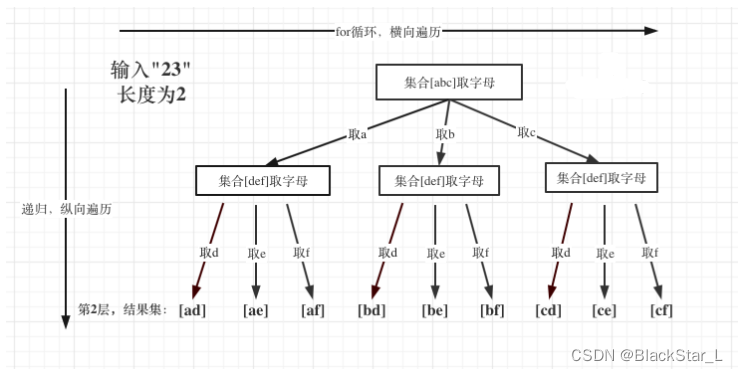
注意:输入1 * #按键等等异常情况。代码中最好考虑这些异常情况,但题目的测试数据中应该没有异常情况的数据,但是要知道会有这些异常,如果是现场面试中,就一定要考虑到。
2.1.4、39. 组合总和 - 可复选同一值
力扣题目链接
回溯法1,candidates角度:
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
path = []
res = []
def backtracking(candidates):
# 大于目标值直接返回空
if sum(path)>=target:
if sum(path)==target and sorted(path) not in res:
# 值存进去之前,提前排序,便于去重
res.append(sorted(path[:]))
return
# 循环整个列表(注意这里会产生重复结果,只是顺序不同)
for i in candidates:
path.append(i)
backtracking(candidates)
path.pop()
backtracking(candidates)
return res
回溯法2,index角度:
这里加上循环的起始索引,并引入一个su_m变量去存储每一步的sum。
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
path = []
res = []
def backtracking(candidates, su_m, startIndex):
# 因为循环进行了优化,所以这里判断会简单许多
if su_m>=target:
if su_m==target:
res.append(path[:])
return
# [2,3,5,7], 7
# 这种循环索引而不是列表值,会优先考虑重复
# 所以不会出现[2,3,2]和[3,2,2]这种重复的排列
# 优先[2,2,2,2]得不到target开始pop
for i in range(startIndex, len(candidates)):
su_m += candidates[i]
path.append(candidates[i])
# 这里起始索引为i,因为可以重复使用
backtracking(candidates, su_m, i)
# 回溯要减去值
su_m -= candidates[i]
path.pop()
backtracking(candidates, 0, 0)
return res
这里还可以简化下:
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
res = []
path = []
def backtracking(ind):
if sum(path)==target:
res.append(path[:])
return
for i in range(ind, len(candidates)):
path.append(candidates[i])
if sum(path)<=target:
backtracking(i)
path.pop()
# 这里直接一个index即可
backtracking(0)
return res
回溯1会产生排列,要去重,而回溯2只产生组合。
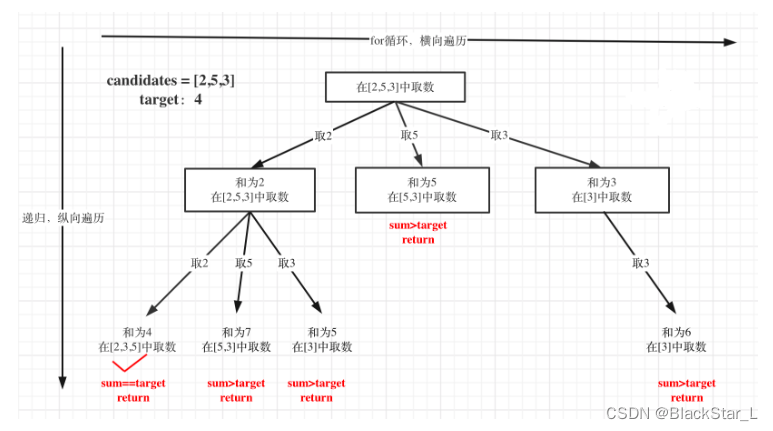
剪枝优化:
当判断sum > target后,就没有必要进入下一层递归。
对总集合排序之后,如果下一层的sum(就是本层的 sum + candidates[i])已经大于target,就可以结束本轮for循环的遍历。
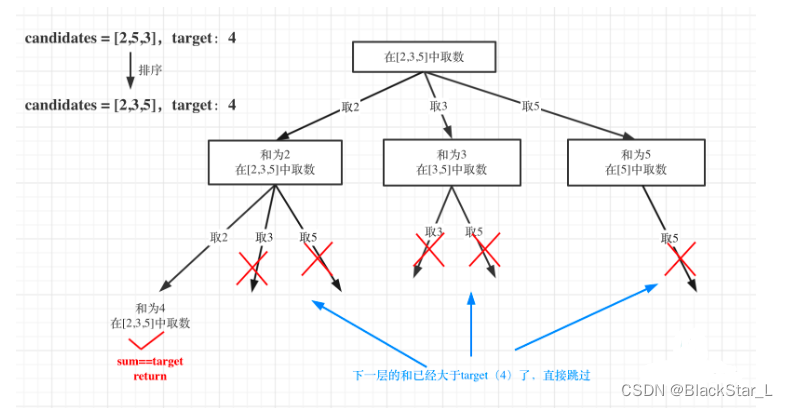
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
path = []
res = []
def backtracking(candidates, su_m, startIndex):
if su_m==target:
res.append(path[:])
return
for i in range(startIndex, len(candidates)):
# 排序后,小的值的和都大于target,后续大的无序继续
# 不排序,结果会出问题
if su_m + candidates[i]> target:
return
su_m += candidates[i]
path.append(candidates[i])
backtracking(candidates, su_m, i)
su_m -= candidates[i]
path.pop()
# 注意要排序
candidates.sort()
backtracking(candidates, 0, 0)
return res
2.1.5、40.组合总和II - 不可复选同一值,但有重复元素
力扣题目链接
本题的难点在于:集合(数组candidates)有重复元素,但还不能有重复的组合。
回溯法1(超时):
把所有组合求出来,去除重复的。
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
path = []
res = []
def backtracking(candidates, su_m, startIndex):
# 这里会有重复的,如[1,1,2,5,6,7,10],8
# 第一个1与第二个1意义不同,[1,2,5] 和 [1,2,6], [1,7]和[1,7]
# 但对结果来说相同。
if su_m == target and path[:] not in res:
res.append(path[:])
return
for i in range(startIndex, len(candidates)):
if su_m + candidates[i]>target:
return
su_m += candidates[i]
path.append(candidates[i])
backtracking(candidates, su_m, i+1)
su_m -= candidates[i]
path.pop()
candidates.sort()
backtracking(candidates, 0, 0)
return res
这里会有重复的,如[1,1,2,5,6,7,10],8。
第一个1与第二个1意义不同,[1,2,5] 和 [1,2,6], [1,7]和[1,7],但对结果来说相同。
所以,只需要第一次的1就可以,同一树层,第一次出现的重复元素会遍历到后面的重复元素,记一次就行,树层的其他相同的直接去掉。
把所有组合求出来,再去重,这么做很容易超时,所以要在搜索的过程中就去掉重复组合。
回溯法2(使用startIndex去重):
既然求结果去重会超时,那么就需要在求的过程中提前去重。
这里直接使用startIndex进行判断去重,同一个树层(for循环内)和上一个元素相等则continue跳过。
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
path = []
res = []
def backtracking(startIndex):
# 这里会有重复的,如[1,1,2,5,6,7,10]
# 第一个1与第二个1意义不同,但对结果来说相同
if sum(path) == target:
res.append(path[:])
return
for i in range(startIndex, len(candidates)):
# 只是用索引来判断重复。这里注意不是i>0
# 因为每一层的元素有更新,得从startIndex开始
# 否则i>0则不存在重复元素了
if i>startIndex and candidates[i] == candidates[i-1]:
continue
su_m += candidates[i]
path.append(candidates[i])
if sum(path)<=target:
backtracking(i+1)
su_m -= candidates[i]
path.pop()
candidates.sort()
backtracking(0)
return res
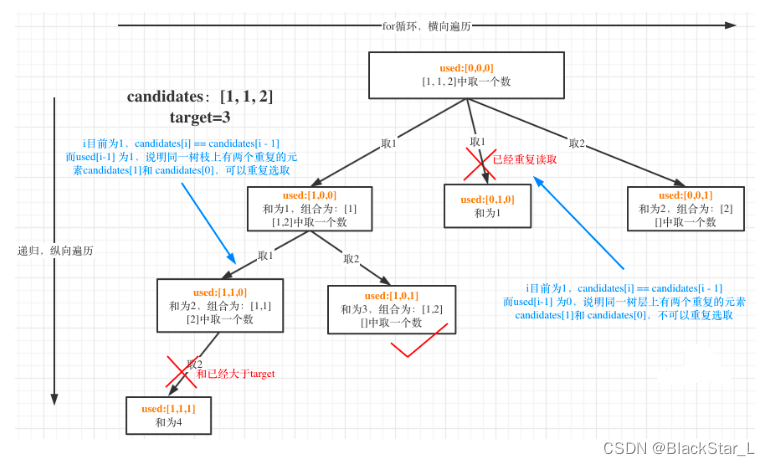
回溯法3(新建used数组去重):
used[i - 1] == true,说明同一树枝candidates[i - 1]使用过,纵向
used[i - 1] == false,说明同一树层candidates[i - 1]使用过,横向
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
path = []
res = []
used = [False] * len(candidates)
def backtracking(startIndex):
# 这里会有重复的,如[1,1,2,5,6,7,10]
# 第一个1与第二个1意义不同,但对结果来说相同
if sum(path) == target:
res.append(path[:])
return
for i in range(startIndex, len(candidates)):
# 上个相同节点没使用过,为False,可以判断为同一树层,则跳过
# 上个相同节点使用过,为True,可以判断为同一树枝,不跳
# 这里注意不同于前面i>startIndex
# 本来i>0不允许任何重复,但used[i-1]==False,表示同一层,从这个相同点开始,(前面一个相同点已经回溯成False了)
if i>0 and candidates[i] == candidates[i-1] and used[i-1]==False:
continue
used[i]=True
path.append(candidates[i])
if sum(path)<=target:
backtracking(i+1)
# 回溯,为了下一轮for loop
used[i]=False
su_m -= candidates[i]
path.pop()
candidates.sort()
backtracking(0)
return res
2.1.6、练习
22. 括号生成
22. 括号生成
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
res = []
path = []
def backtracking(l, r):
if l==n and r==n:
res.append(''.join(path))
if l<n:
path.append('(')
backtracking(l+1,r)
path.pop()
if r<l:
path.append(')')
backtracking(l,r+1)
path.pop()
backtracking(0,0)
return res

2.2、分割问题
2.2.1、131. 分割回文串 - 回溯附加条件
力扣题目链接
回溯+双指针:
class Solution:
def partition(self, s: str) -> List[List[str]]:
res = []
path = []
# 判断回文的函数
# 正反序
# def isPalindrome(s, start, end):
# if s[start:end+1] == s[start:end+1][::-1]:
# return True
# return False
# 双指针
def isPalindrome(s, start, end):
while start<end:
if s[start] != s[end]:
return False
start+=1
end-=1
return True
def backtracking(s, startIndex):
if startIndex>= len(s):
res.append(path[:])
return
for i in range(startIndex, len(s)):
# 判断是否为回文,是再添加到path
# 不是回文,则切割失败,后续操作跳过
if isPalindrome(s, startIndex, i):
path.append(s[startIndex:i+1])
else:
continue
backtracking(s, i+1)
path.pop()
backtracking(s, 0)
return res
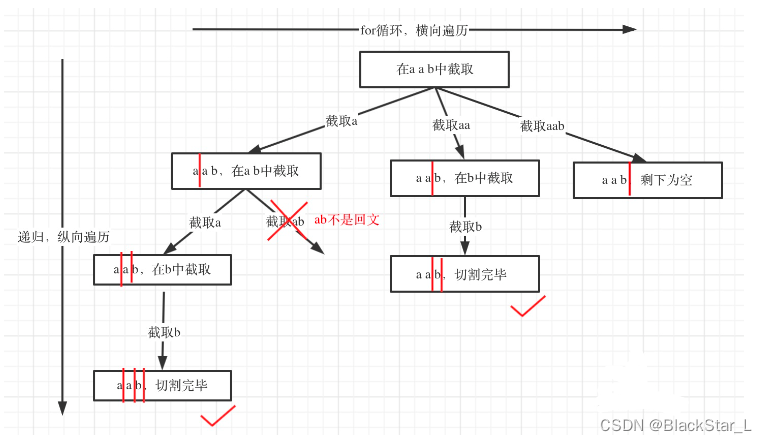
回溯+正反序:
class Solution:
def partition(self, s: str) -> List[List[str]]:
res = []
path = []
def backtracking(ind):
if ind==len(s):
res.append(path[:])
for i in range(ind, len(s)):
if s[ind:i+1]!=s[ind:i+1][::-1]:
continue
path.append(s[ind:i+1])
backtracking(i+1)
path.pop()
backtracking(0)
return res

2.2.2、93.复原IP地址 - 回溯附加条件
力扣题目链接
回溯法1, 使用index:
思路同上一题,切割成4份为终止标准,结合startIndex判断是否遍历完整字符串,将合法的结果用’.'拼接即可。
class Solution:
def restoreIpAddresses(self, s: str) -> List[str]:
res = []
path = []
# 判断是否合法
# 1. 0-255 之间,闭区间
# 2. 当长度大于1时(或不为0),首位不能为0
def isValid(s, start, end):
if 0<=int(s[start:end+1])<=255 and \
(s[start:end+1]=='0' or s[start:end+1].lstrip('0')==s[start:end+1]):
# 首位不能为0,则去除首位的0后还是原来的字符串则首位无0
return True
return False
def backtracking(startIndex):
# 终止条件为截取了4段
if len(path)==4:
# 截取4段,并且索引到了尾部,即取了所有字符
if startIndex == len(s):
# 将结果用.拼接起来
res.append('.'.join(path[:]))
return
# 遍历字符串
for i in range(startIndex, len(s)):
if isValid(s, startIndex, i) and len(path)<=4:
path.append(s[startIndex:i+1])
backtracking(i+1)
path.pop()
backtracking(0)
return res
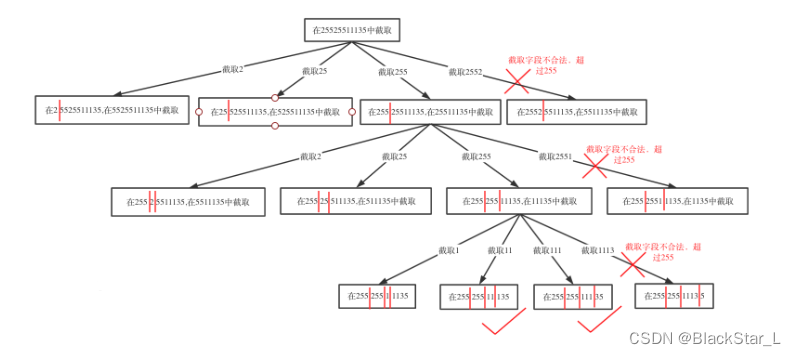
回溯法2,使用string:
class Solution:
def restoreIpAddresses(self, s: str) -> List[str]:
res=[]
path=[]
def isvalid(string):
if len(string)==len(str(int(string))) and 0<=int(string)<=255:
return True
return False
def dfs(s):
if len(path)==4 and s:
return False
if len(path)==4 and not s:
res.append('.'.join(path[:]))
return
for i in range(len(s)):
if isvalid(s[:i+1]):
path.append(s[:i+1])
dfs(s[i+1:])
path.pop()
dfs(s)
return res

2.3、子集问题
2.3.1、78. 子集 - 整棵遍历数
力扣题目链接
注:幂集就是集合的所有子集。
回溯法:
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
res = []
path = []
def backtracking(nums, startIndex):
# 子集就是遍历整个树
res.append(path[:])
if startIndex == len(nums):
return
for i in range(startIndex, len(nums)):
path.append(nums[i])
backtracking(nums, i+1)
path.pop()
backtracking(nums, 0)
return res
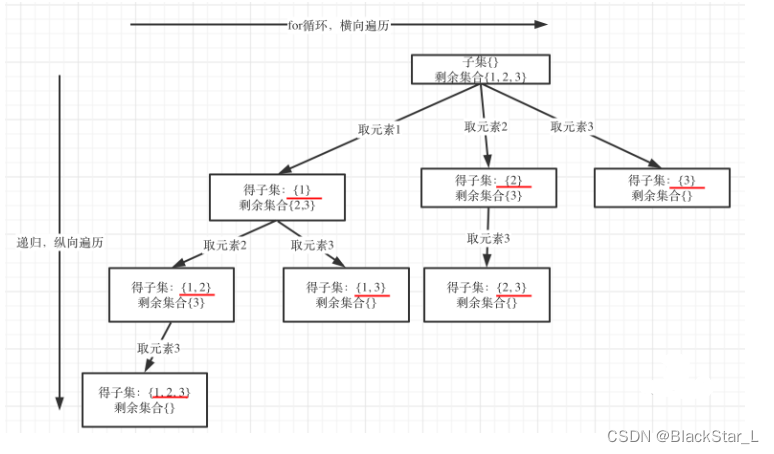
从上图可知,求取子集问题,不需要任何剪枝,因为子集就是要遍历整棵树。
2.3.2、90. 子集 II - 乱序+重复元素+去重复值
力扣题目链接
思路同 40. 数组总和 II,即去重,去掉同一树层的重复节点。
回溯法:
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
res = []
path = []
def backtracking(startIndex):
res.append(path[:])
if startIndex == len(nums):
return
for i in range(startIndex, len(nums)):
# 同一树层,相似的则先去掉
if i>startIndex and nums[i]==nums[i-1]:
continue
path.append(nums[i])
backtracking(i+1)
path.pop()
# 需要排序,便于把相似的排到一起
nums.sort()
backtracking(0)
return res

注意: 一定要对元素进行排序,这样我们才方便通过相邻的节点来判断是否重复使用了。
子集题做完建议试试 2.6.1、491.递增子序列
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
res = []
path = []
def backtracking(ind):
res.append(path[:])
if ind==len(nums):
return
# 每一层标记重复
used = set()
for i in range(ind, len(nums)):
# 有重复的跳过,前面已经遍历过
if nums[i] in used:
continue
# 按层添加
used.add(nums[i])
path.append(nums[i])
backtracking(i+1)
path.pop()
# nums.sort()
backtracking(0)
return res

2.4、排列问题
排列是有序的,也就是说 [1,2] 和 [2,1] 是两个集合,这和之前分析的子集以及组合所不同的地方。
2.4.1、46.全排列
力扣题目链接
回溯法1,数组截断传递:
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
res = []
path = []
def backtracking(nums):
# 每次传入的nums是变动的,逐渐变为空,所以不能len(path)==len(nums)
if not nums:
res.append(path[:])
return
# 从索引0开始,因为每次都要取到所有数
for i in range(len(nums)):
path.append(nums[i])
# 去掉被选中的nums[i],选取其他段拼在一起
backtracking(nums[:i]+nums[i+1:])
path.pop()
backtracking(nums)
return res
回溯法2,used数组:
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
res = []
path = []
# 创建一个flag数组,保存结果,是否使用过
used_list = [False]*len(nums)
def backtracking(nums, used_list):
# 每次传入的nums是固定的,则len(path)==len(nums)
if len(path) == len(nums):
res.append(path[:])
return
for i in range(len(nums)):
# 已经使用过,则去重
if used_list[i]==True:
continue
used_list[i] = True
path.append(nums[i])
backtracking(nums, used_list)
used_list[i] = False
path.pop()
backtracking(nums, used_list)
return res
回溯法3,去掉used:
最简单的写法,因为无重复元素,所以path可以代替used_list。
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
res = []
path = []
def backtracking(nums):
# 每次传入的nums是固定的,则len(path)==len(nums)
if len(path) == len(nums):
res.append(path[:])
return
for i in range(len(nums)):
# 因为本题为无重复元素,所以path内的元素是唯一的
if nums[i] in path:
continue
path.append(nums[i])
backtracking(nums)
path.pop()
backtracking(nums)
return res
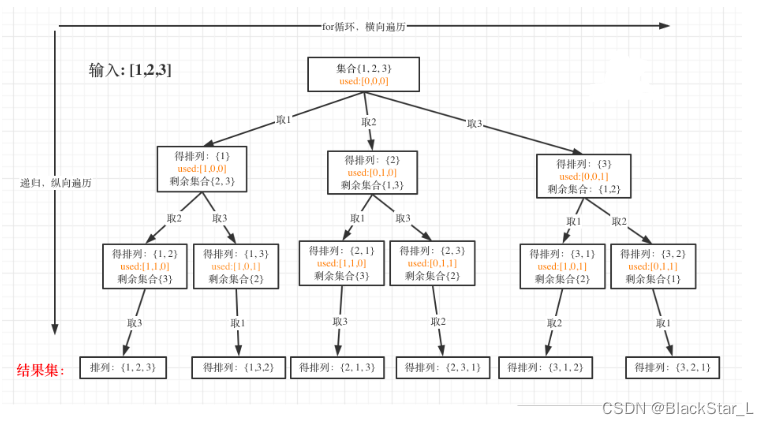
可以看出元素1在[1,2]中已经使用过了,但是在[2,1]中还要在使用一次1,所以处理排列问题就不用使用startIndex了。
排列问题的不同:
每层都是从0开始搜索而不是startIndex
需要used数组记录path里都放了哪些元素了
2.4.2、47.全排列 II
力扣题目链接
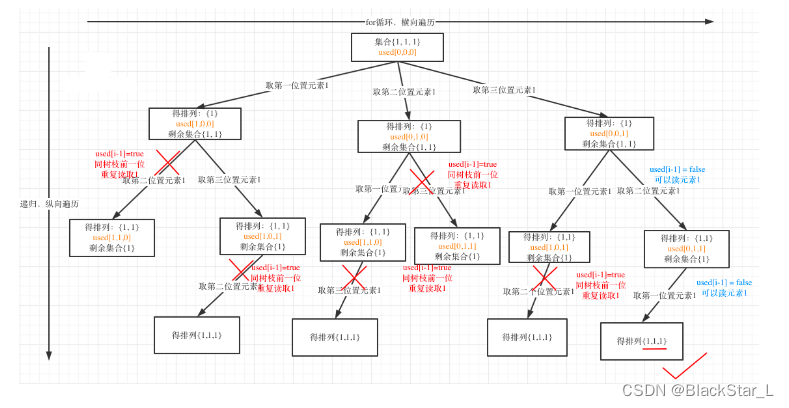
这里必须使用used_list布尔列表,一个是原来的作用,即判断使用使用过;另一个是判断,在同一层,和此元素相同的值之前是否使用过。使用过直接跳过,否则是相同的操作结果。
class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
res = []
path = []
used_list = [False]*len(nums)
def backtracking(nums, used_list):
if len(nums) == len(path):
res.append(path[:])
return
for i in range(len(nums)):
# 每次递归,都是所有元素
# 1.该元素自身被使用过,continue
if used_list[i] == True:
continue
# 2.该元素同一层有之前有重复,则只算一次,则这一次continue
# used_list[i-1]==True表示同一层之前使用过
# 同一层去重效率高,即取False效率比True高
if (i>0 and nums[i]==nums[i-1]) and used_list[i-1]==False:
continue
used_list[i] = True
path.append(nums[i])
backtracking(nums, used_list)
used_list[i] = False
path.pop()
nums.sort()
backtracking(nums, used_list)
return res

2.5、应用型类似问题
2.5.1、491.递增子序列 (和子集问题很像)- 非排序+重复元素+去重
力扣题目链接
本题求自增子序列,是不能对原数组经行排序的,排完序的数组都是自增子序列了,所以不能使用之前的去重逻辑!
回溯法+集合去重:
#深度遍历中每一层都会有一个全新的usage_list用于记录本层元素是否重复使用
class Solution:
def findSubsequences(self, nums: List[int]) -> List[List[int]]:
res = []
path = []
def backtracking(startIndex):
if len(path)>=2:
res.append(path[:])
if startIndex==len(nums):
return
# 这里要放在内部,因为每一层子树都要去重
# 用来记录非重复的元素,用来去重判断
used_list = set()
# 单层递归逻辑
# 深度遍历中每一层都会有一个全新的usage_list用于记录本层元素是否重复使用
for i in range(startIndex, len(nums)):
# 这个去重只能判断排序后相邻的数组
# 所以像[4,7,6,7]在这里不可用
#if i>startIndex and if nums[i] == nums[i-1]:
# continue
# path非空,且后一个小于前一个,即小于path的最后一个元素
# 或者 同一树层后面重复出现,不同于前面的相邻重复出现
if (path and nums[i]<path[-1]) or nums[i] in used_list:
continue
used_list.add(nums[i])
path.append(nums[i])
backtracking(i+1)
path.pop()
backtracking(0)
return res
回溯法+哈希表去重:
class Solution:
def findSubsequences(self, nums: List[int]) -> List[List[int]]:
res = []
path = []
def backtracking(nums, startIndex):
if len(path)>=2:
res.append(path[:])
if startIndex==len(nums):
return
# 使用哈希表去重,也就是数组或列表
used_list = [False] * 201 # 使用列表去重,题中取值范围[-100, 100]
for i in range(startIndex, len(nums)):
if (path and nums[i]<path[-1]) or used_list[nums[i]+100]==True:
continue
# +100,将-100 - 100变为0 - 200
used_list[nums[i]+100] = True
path.append(nums[i])
backtracking(nums, i+1)
path.pop()
backtracking(nums, 0)
return res
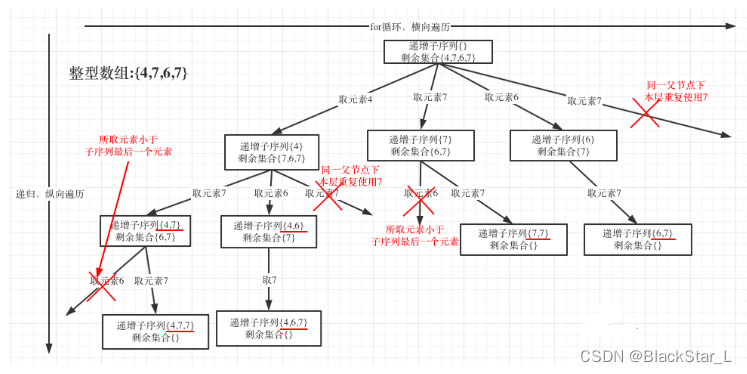
在图中可以看出,同一父节点下的同层上使用过的元素就不能在使用了。与前面的同一层相邻重复的不同。

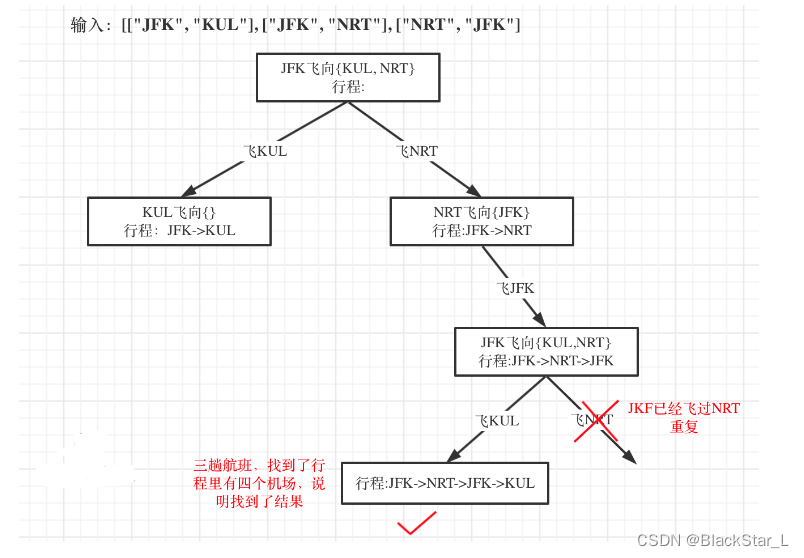
2.5.2、332.重新安排行程(和2.1.3、17. 电话号码的字母组合 很像)
力扣题目链接
这一题可参考 2.1.3、17. 电话号码的字母组合 - 双层回溯,自己创建映射进行遍历回溯,只不过,电话号码里面,是寻找所有组合,每个数字对于字母的选择是所有,而且能重复选择;而行程里面,每个地点对应的地点列表里,有效的只有部分,并且在选择了某地点后,下一次的地点列表需要将其去除。如何将其去除这是一个难点。
回溯法1(普通解法,超时):
class Solution:
def findItinerary(self, tickets: List[List[str]]) -> List[str]:
res = []
path = []
used_list = [False]*len(tickets)
def backtracking(tickets):
if len(path) == len(tickets):
res.append(path[:])
return
# 每次遍历整个list,前面的通用解法,但对于这一题,这样会超时
for i in range(len(tickets)):
if used_list[i] == True:
continue
if i>0 and tickets[i] == tickets[i-1] and used_list[i-1]==True:
continue
if (path and (path[-1][-1]==tickets[i][0])) or (not path and tickets[i][0] == 'JFK'):
used_list[i] = True
path.append(tickets[i])
backtracking(tickets)
used_list[i] = False
path.pop()
backtracking(tickets)
# 将结果按字典排序
final = sorted(res)[0]
r = []
# 所有list只取第一个值,加上最后一个list取最后一个值
for i in range(len(final)):
r.append(final[i][0])
if i == len(final)-1:
r.append(final[i][1])
return r
回溯法2:
重新设置tickets为一个新的对象进行简化处理,这样就无需遍历整个tickets。
class Solution:
def findItinerary(self, tickets: List[List[str]]) -> List[str]:
res = []
path = ['JFK']
# 创建一个空字典,值为空list
ticket_dict = defaultdict(list)
for item in tickets:
ticket_dict[item[0]].append(item[1])
# 排序1 提前排序 或者在内部排序
for t in ticket_dict:
ticket_dict[t].sort()
'''
tickets_dict里面的内容是这样的
{'JFK': ['SFO', 'ATL'], 'SFO': ['ATL'], 'ATL': ['JFK', 'SFO']})
'''
# 根据字典的key去延伸到value再对应到下一个key......以此类推
def backtracking(start_point):
if len(path) == len(tickets)+1:
return True
# 内部排序,咱们使用外面的排序方法,只用遍历一次
# ticket_dict[start_point].sort()
for _ in ticket_dict[start_point]:
# 取出一个值,选择一个落地点
end_point = ticket_dict[start_point].pop(0)
path.append(end_point)
# 只要找到一个就可以直接返回了,这里设置成bool
# 并且path直接为正确结果,跳过path.pop()还原
if backtracking(end_point):
return True
path.pop()
ticket_dict[start_point].append(end_point)
backtracking('JFK')
return path
做回溯相关问题时,先思考以下几点:
排列或组合?有无序?是否有重复元素?有什么不同,需要什么或不需要什么?
总结如下:
| 回溯问题 | 组合 | 排列 | 幂集 |
|---|---|---|---|
| 回溯函数参数 | 使用startIndex,每进一层(startIndex, len(nums)),即找startIndex后面的元素进行组合,防止重复值。 | 任意参数。有重复组合值,只是排列不同,startIndex无意义,使用used布尔列表,为True则表示访问过,去掉。 | 同组合 |
| 额外变量 | 只需startIndex即可 / used布尔list / 同一层的used集合 | used布尔list | 同组合 |
| 遍历顺序 | 从startInde开始搜索:(startIndex, len(nums)) | 从头开始搜索(len(nums) | 同组合 |
| 有重复元素+无序/有序 | (无序则先进行排序)下面三种不同方法排除重复组合,直接continue: [1] i>startIndex and nums[i]==nums[i-1] ;[2] i>0 and nums[i]==nums[i-1] and nums[i-1]=False ;[3] 同一层 used=set() ,nums[i] in used,used只有append无pop。 | (无序则先进行排序)除了自身是否使用过进行判断,其余判断同前面组合,对同一层是否重复使用进行判断。 | 同组合 |
| 无重复元素+无序/有序 | (无需排序)常规回溯写法 | (无需排序)常规回溯写法+used判断/path代替used | 同组合 |
| 结果 | 同长度组合 | 同长度排列 | (不同长度)节点上所有元素。当数组无重复元素,幂集的结果大小为 2 数组长度 2^{数组长度} 2数组长度。 |
注意: 这是常规解法,对本文章以及很多特定其他解法没有包含进去,等算法达到了一定的水平可以自行创造。

2.6、棋盘问题

2.6.1、HJ43 迷宫问题
华为机试牛客网链接
回溯法:
# 字符串转数字和迷宫
h, w = map(int, input().split())
maze = []
for i in range(h):
maze.append(list(map(int, input().split())))
# 初始化
# 起点
result = [(0, 0)]
# 走过的路径进行标记,防止回溯死循环
maze[0][0] = 3
# 判断该点是否合法
# 1.范围,2.路或墙
def isVaild(x, y):
if 0 <= x < h and 0 <= y < w and maze[x][y] == 0:
return True
return False
# 回溯
def backtracking(x, y):
# 打印每一步的坐标点
# print(x,y)
# 终止条件,到达右下角终点
if x == h - 1 and y == w - 1:
# result.append((x, y))
return result
"""
回溯前,从第一个方向开始
第一个条件先判断下一步是否合法
合法再进行深度优先搜索
1.同时对走过的路径进行标记为3
2.将坐标加入到result结果中
搜索成功,1和2成立
搜索失败,进行回溯:
1. 将走过的路径进行回溯,但不能改为原值0,可改为2,另一个值,或者不改也可以
2. 将result进行回溯,pop退出结果
选择下一个方向
如果四个方向都失败,则返回False,说明该方向的深度优先无法走到终点
"""
# 下
if isVaild(x + 1, y):
result.append((x + 1, y))
maze[x + 1][y] = 3
if backtracking(x + 1, y):
return True
# 回溯
result.pop()
maze[x + 1][y] = 2
# 上
if isVaild(x - 1, y):
result.append((x - 1, y))
maze[x - 1][y] = 3
if backtracking(x - 1, y):
return True
# 回溯
result.pop()
maze[x - 1][y] = 2
# 左
if isVaild(x, y - 1):
result.append((x, y - 1))
maze[x][y - 1] = 3
if backtracking(x, y - 1):
return True
# 回溯
result.pop()
maze[x][y - 1] = 2
# 右
if isVaild(x, y + 1):
result.append((x, y + 1))
maze[x][y + 1] = 3
if backtracking(x, y + 1):
return True
# 回溯
result.pop()
maze[x][y + 1] = 2
# 上下左右都不行,则返回False
return False
backtracking(0, 0)
print(result)
print(maze)
测试输入:
h,w = map(int, '5 5'.split())
maze = []
deal = ['0 1 0 0 0', '0 1 1 1 0', '0 0 0 0 0','0 1 1 1 0','0 0 0 1 0']
for i in deal:
maze.append(list(map(int, i.split())))
"""
[[0, 1, 0, 0, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 0, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 1, 0]]
"""
结果:
0 0
1 0
2 0
3 0
4 0
4 1
4 2
2 1
2 2
2 3
2 4
3 4
4 4
[(0, 0), (1, 0), (2, 0), (2, 1), (2, 2), (2, 3), (2, 4), (3, 4), (4, 4)]
[[3, 1, 0, 0, 0],
[3, 1, 1, 1, 0],
[3, 3, 3, 3, 3],
[2, 1, 1, 1, 3],
[2, 2, 2, 1, 3]]

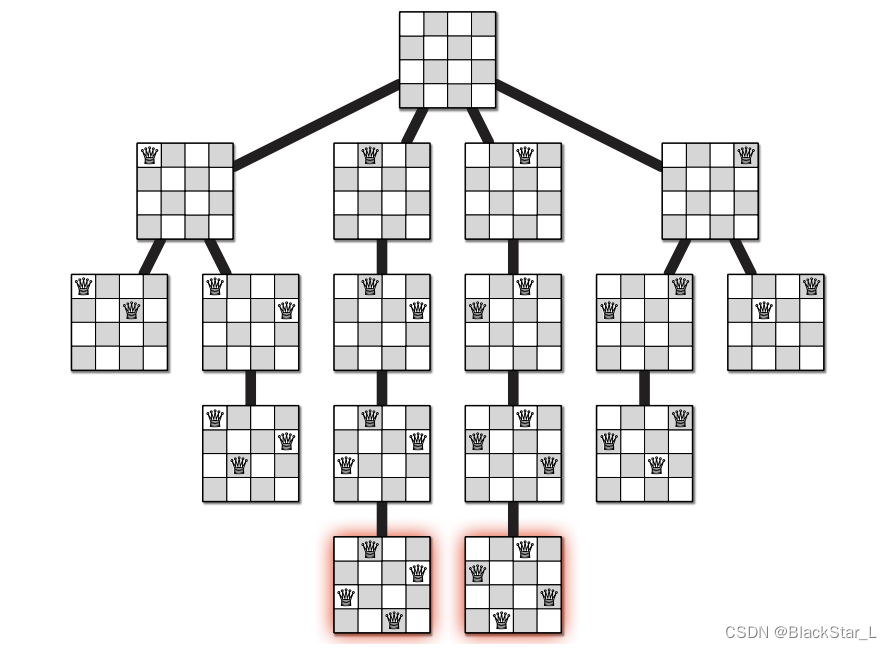
2.6.2、51. N 皇后
力扣题目链接
回溯法:
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
res = []
board = [['.']*n for _ in range(n)]
# 判断是否合法
def isVaild(board, row, col):
# 1. 判断同一列是否冲突
for i in range(row+1):
if board[i][col] == 'Q':
return False
# 2.判断左上是否冲突
tmp_row = row
tmp_col = col
while 0<=tmp_row<n and 0<=tmp_col<n:
if board[tmp_row][tmp_col]== 'Q':
return False
tmp_row-=1
tmp_col-=1
# 3.判断右上是否冲突
tmp_row = row
tmp_col = col
while 0<=tmp_row<n and 0<=tmp_col<n:
if board[tmp_row][tmp_col]== 'Q':
return False
tmp_row-=1
tmp_col+=1
return True
# 每一行进行遍历
def backtracking(row, board):
if row == n:
tmp = []
for i in board:
tmp.append(''.join(i))
res.append(tmp)
return
# 每一行的每一列进行选取
for col in range(n):
if not isVaild(board, row, col):
continue
board[row][col] = 'Q'
# 进入下一行
backtracking(row+1, board)
board[row][col] = '.'
backtracking(0, board)
return res
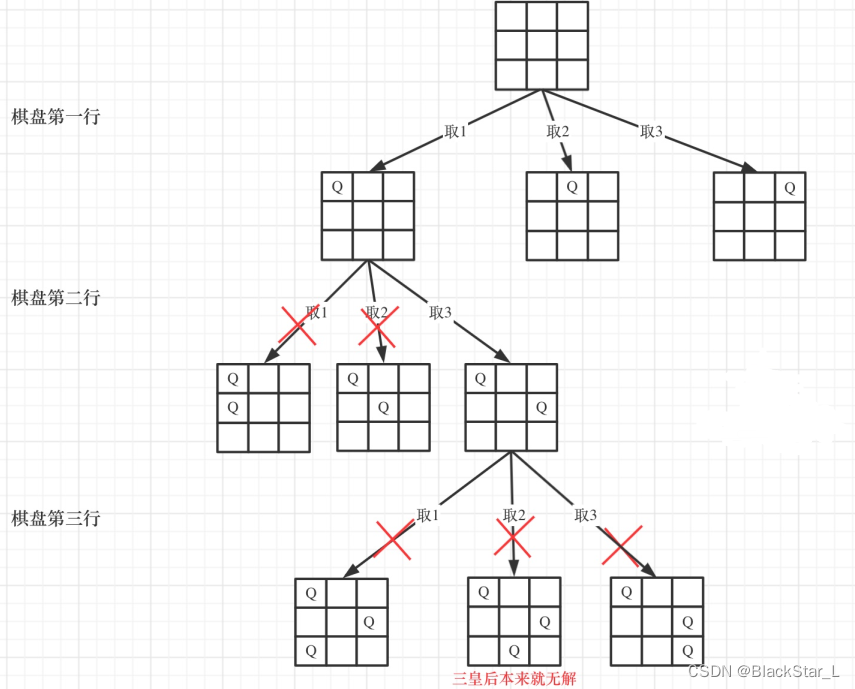
皇后们的约束条件:
- 不能同行
- 不能同列
- 不能同斜线
符合条件则继续下一行,否则同行的下一列。
这题是hard题其实难度并不大,当做 2.1.3、17. 电话号码的字母组合 和 332.重新安排行程 来做,每一行为索引进行遍历,内部每一列进行遍历回溯。
难点在于判断条件,即约束条件上是否有Q。我们一般拆成4个部分,横,竖,正斜,反斜,但实际上,横无需判断,因为每一行的行为树根,这个只会按顺序递增,而由此引出子树列才需要回溯,只会产生一个Q。并且斜左下与斜右下也无需遍历,因为一定为空,一定没有Q,因为还没遍历到那个位置,所以咱们的判断以该点为水平线的上面部分为区间即可,这样可以降低复杂度。

2.6.3、37. 解数独
力扣题目链接
回溯法:
class Solution:
def solveSudoku(self, board: List[List[str]]) -> None:
"""
Do not return anything, modify board in-place instead.
"""
def isVaild(row, col, val, board):
# 判断同一行是否冲突
for i in range(9):
if board[row][i] == str(val):
return False
# 判断同一列是否冲突
for i in range(9):
if board[i][col] == str(val):
return False
# 判断同一宫是否冲突
start_row = (row//3)*3
start_col = (col//3)*3
for i in range(start_row, start_row+3):
for j in range(start_col, start_col+3):
if board[i][j] == str(val):
return False
return True
# 若有解返回True,无解返回False
def backtracking(board):
# 这里遍历完即是终止条件
# 遍历整个表,行和列
for i in range(len(board)):
for j in range(len(board[0])):
# 若空格内已经有数字,则跳过
if board[i][j] != '.':
continue
# 逐渐填入1-10
for k in range(1, 10):
# 有效则继续递归
if isVaild(i, j, k, board):
board[i][j] = str(k)
if backtracking(board):
return True
# 回溯
board[i][j] = '.'
# 若数字1-9都不能成功填入空格,返回False无解
return False
# 有解,说明已经填满了,到了最后一步,所有的board[i][j] != '.'
return True
backtracking(board)
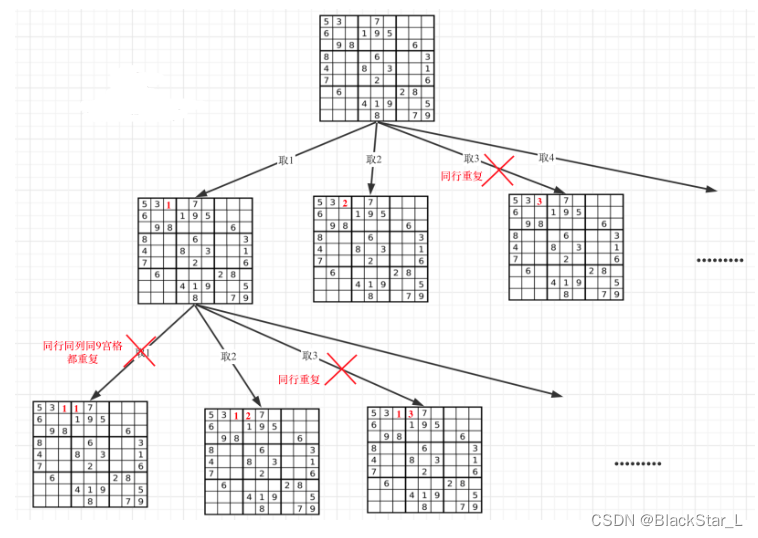
N皇后问题是因为每一行每一列只放一个皇后,只需要一层for循环遍历一行,递归来来遍历列,然后一行一列确定皇后的唯一位置。
本题就不一样了,本题中棋盘的每一个位置都要放一个数字,并检查数字是否合法,解数独的树形结构要比N皇后更宽更深。
这里需要的是一个二维的递归(也就是两个for循环嵌套着递归),这个二维的递归与下一章中的深搜与广搜有很深的联系,如果你能理解其一,对这题或者下一章的题目的理解都非常的简单。
一个for循环遍历棋盘的行,一个for循环遍历棋盘的列,一行一列确定下来之后,递归遍历这个位置放9个数字的可能性。如果一行一列确定下来了,这里尝试了9个数都不行,说明这个棋盘找不到解决数独问题的解。
判断棋盘是否合法有如下三个维度:
- 同行是否重复
- 同列是否重复
- 9宫格里是否重复
同时,一定要注意,最后的两层循环之外,需要return True,因为棋盘都填满了,这是满足结果的,需要传回布尔True给if backtracking()去判断,从而继续return True,防止后续的回溯而还原结果,导致即便搜到了结果,因为回溯还原了,最后board还是原来的空的。
同时,题目要求只有一个结果时,我们把backtracking当做布尔if去判断,通过return True防止回溯。
当题目要求有多个结果时,我们就当普通的backtracking为一行,回溯前将结果通过path存到res中。
三、深搜DFS与广搜BFS
深广搜问题相比回溯问题,少了退回的操作,但思路大致相似,所以该类型题目会更加容易。
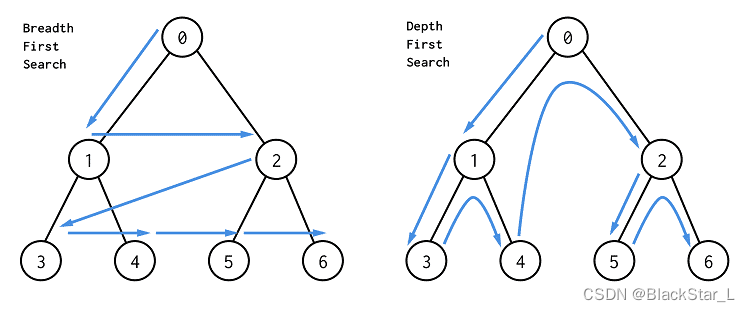
3.1、岛屿问题
基本上,能用dfs做的题目也能用bfs来做,所以可以尝试用这两种方法去解题。这样对该类型算法的理解会更加深刻。

200. 岛屿数量
200. 岛屿数量
非常常规和经典的DFS和BFS题目。
1. 深度优先搜索DFS
dfs题目的模板与回溯法类似,但是没有退回操作,因为都是有效操作。
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
# 避免重复,将结果存进来,或者grid[i][j]=0遍历过变成湖泊避免死循环
grid_set = set()
res = 0
def dfs(i, j):
for x, y in (i+1, j), (i-1, j), (i, j+1), (i, j-1):
if 0<=x<len(grid) and 0<=y<len(grid[0]) and grid[x][y]=='1' and (x,y) not in grid_set:
# 遍历过的结果存到grid_set
grid_set.add((x,y))
# 将符合条件的(x,y)继续迭代
dfs(x,y)
for i in range(len(grid)):
for j in range(len(grid[0])):
# 为陆地,并且没被遍历过
if grid[i][j]=='1' and (i,j) not in grid_set:
res+=1
grid_set.add((i,j))
dfs(i,j)
return res
因为整个地图给到我们,我们不用将结果存起来去判断重复,直接遍历过的变成 0 湖泊就行了,那么少一个grid_set的空间以及搜索时间,效率会提高:
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
res = 0
def dfs(i, j):
grid[i][j]='0' # 这里改成非'1'的任何值都可以
for x, y in (i+1, j), (i-1, j), (i, j+1), (i, j-1):
if 0<=x<len(grid) and 0<=y<len(grid[0]) and grid[x][y]=='1':
# 将符合条件的(x,y)继续迭代
dfs(x,y)
for i in range(len(grid)):
for j in range(len(grid[0])):
# 为陆地,并且没被遍历过
if grid[i][j]=='1':
res+=1
dfs(i,j)
return res
2. 广度优先搜索 BFS
from collections import deque
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
res = 0
for i in range(len(grid)):
for j in range(len(grid[0])):
# 为陆地,并且没被遍历过
if grid[i][j]=='1':
res+=1
grid[i][j]=='0'
# 用队列代替列表存储,加快速度
neighbors = deque([(i,j)])
# 从一个点开始向周围扩散,广度优先,扩散到完成,退出,找下一个点
while neighbors:
# 从左起点开始取所有点
# 为什么从左开始?先搜索完该点的第一外层
# 随后第二外层等等依次继续
xi, yj = neighbors.popleft()
# 后面的代码同dfs,但是内部没有嵌套dfs,也就不会无限的深度找,而是找一次,即外层一圈即可。
for x, y in (xi+1, yj), (xi-1, yj), (xi, yj+1), (xi, yj-1):
if 0<=x<len(grid) and 0<=y<len(grid[0]) and grid[x][y]=='1':
neighbors.append((x, y))
grid[x][y]='0'
return res
1254. 统计封闭岛屿的数目
1254. 统计封闭岛屿的数目
求封闭的个数,那么分为非封闭与封闭岛屿,需要在搜索的过程中对不符合条件的进行标记,被标记上的岛屿总数不会+1。
1.深度优先搜索DFS
遍历所有面积,去除与边界连通的面积,即边界位置有1岛屿的。
class Solution:
def closedIsland(self, grid: List[List[int]]) -> int:
row = len(grid)
col = len(grid[0])
res = 0
def dfs(i, j):
# 同样,遍历过的点进行标注,防止死循环或重复遍历
grid[i][j]=1
for x, y in (i+1, j), (i-1, j), (i, j+1), (i, j-1):
if 0<=x<row and 0<=y<col and grid[x][y]==0:
# 有不符合条件的点,该面积标注为0,即不合理
if x==0 or x==row-1 or y==0 or y==col-1:
nonlocal flag
flag=0
dfs(x, y)
for i in range(1, row-1):
for j in range(1, col-1):
flag = 1
if grid[i][j]==0:
dfs(i, j)
# 符合条件,无边界为0或row、col长度的面积则合理
if flag:
res+=1
return res
2.广度优先搜索
from collections import deque
class Solution:
def closedIsland(self, grid: List[List[int]]) -> int:
row = len(grid)
col = len(grid[0])
res = 0
for i in range(1, row-1):
for j in range(1, col-1):
flag = 1
if grid[i][j]==0:
grid[i][j]=1
# 同样使用队列代替列表加速
neighbors = deque([(i, j)])
while neighbors:
xi, yj = neighbors.popleft()
for x, y in (xi+1, yj),(xi-1, yj),(xi,yj+1),(xi,yj-1):
if 0<=x<row and 0<=y<col and grid[x][y]==0:
# 判断条件,不符合条件的标记为0
if x==0 or x==row-1 or y==0 or y==col-1:
flag = 0
# 添加下一圈点以及避免重复进行相反值标记
neighbors.append((x,y))
grid[x][y]=1
# 符合条件,无边界为0或row、col长度的面积则合理
if flag:
res+=1
return res
3.深度优先/广度优先 去除边界连通面积
class Solution:
def countSubIslands(self, grid1: List[List[int]], grid2: List[List[int]]) -> int:
row = len(grid1)
col = len(grid1[0])
res = 0
# 常规dfs
def dfs(i,j):
grid2[i][j]=0
for x, y in (i+1,j),(i-1,j),(i,j+1),(i,j-1):
if 0<=x<row and 0<=y<col and grid2[x][y]==1:
dfs(x ,y)
# 求B在A中的子集,B有A没有的点,延伸的面积全部变成0
for i in range(row):
for j in range(col):
if grid1[i][j]==0 and grid2[i][j]==1:
dfs(i,j)
# 最后剩下的grid2中的1的岛屿即A的子集
for i in range(row):
for j in range(col):
if grid2[i][j]==1:
res+=1
dfs(i,j)
return res
1020.飞地的数量
1020.飞地的数量
这题同上思路,不过不是统计面积,无需再dfs,而是统计为1的格子数量,那么直接遍历即可。
class Solution:
def numEnclaves(self, grid: List[List[int]]) -> int:
row = len(grid)
col = len(grid[0])
res = 0
# 同上
def dfs(i,j):
grid[i][j]=0
for x, y in (i+1,j),(i-1,j),(i,j+1),(i,j-1):
if 0<=x<row and 0<=y<col and grid[x][y]==1:
dfs(x,y)
for i in range(row):
if grid[i][0]==1:
dfs(i,0)
if grid[i][col-1]==1:
dfs(i,col-1)
for j in range(col):
if grid[0][j]==1:
dfs(0,j)
if grid[row-1][j]==1:
dfs(row-1,j)
# 统计图上都是1的格子数量
for i in range(1, row-1):
for j in range(1, col-1):
if grid[i][j]==1:
res+=1
return res
广度优先的写法也很简单,同上。
695. 岛屿的最大面积
695. 岛屿的最大面积
同前面,将所有面积计算出来,每次max最大的即可。
1.深度优先搜索DFS
class Solution:
def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
row = len(grid)
col = len(grid[0])
# 保存最大的结果
max_area = 0
def dfs(i,j):
grid[i][j]=0
# 这里是关键,每遍历一个点,面积+1
nonlocal area
area+=1
for x, y in (i+1, j),(i-1,j),(i,j+1),(i,j-1):
if 0<=x<row and 0<=y<col and grid[x][y]==1:
dfs(x,y)
for i in range(row):
for j in range(col):
if grid[i][j]==1:
area = 0
dfs(i,j)
# 取最大的面积
max_area = max(max_area, area)
return max_area
2.广度优先搜索 BFS
from collections import deque
class Solution:
def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
row = len(grid)
col = len(grid[0])
max_area = 0
for i in range(row):
for j in range(col):
if grid[i][j]==1:
area = 0
grid[i][j]=0
neighbors = deque([(i,j)])
while neighbors:
xi, yj = neighbors.popleft()
# 面积+1
area+=1
for x, y in (xi+1, yj), (xi-1, yj), (xi, yj+1),(xi,yj-1):
if 0<=x<row and 0<=y<col and grid[x][y]==1:
neighbors.append((x,y))
grid[x][y]=0
max_area = max(area, max_area)
return max_area
1905. 统计子岛屿
1905. 统计子岛屿
class Solution:
def countSubIslands(self, grid1: List[List[int]], grid2: List[List[int]]) -> int:
row = len(grid1)
col = len(grid1[0])
res = 0
def dfs(i,j):
grid2[i][j]=0
for x, y in (i+1,j),(i-1,j),(i,j+1),(i,j-1):
if 0<=x<row and 0<=y<col and grid2[x][y]==1:
dfs(x ,y)
# 求B在A中的子集,B有A没有的点,延伸的面积全部变成0
for i in range(row):
for j in range(col):
if grid1[i][j]==0 and grid2[i][j]==1:
dfs(i,j)
# 最后剩下的grid2中的1的岛屿即A的子集
for i in range(row):
for j in range(col):
if grid2[i][j]==1:
res+=1
dfs(i,j)
return res
广度优先的写法也很简单,同上。
130. 被围绕的区域
130. 被围绕的区域
class Solution:
def solve(self, board: List[List[str]]) -> None:
row = len(board)
col = len(board[0])
def dfs(i,j):
board[i][j]='Z'
for x, y in (i+1, j),(i-1, j),(i, j+1),(i,j-1):
if 0<=x<row and 0<=y<col and board[x][y]=='O':
dfs(x,y)
# 两竖边界
for i in range(row):
if board[i][0]=='O':
dfs(i,0)
if board[i][col-1]=='O':
dfs(i,col-1)
# 两横边界
for j in range(col):
if board[0][j]=='O':
dfs(0,j)
if board[row-1][j]=='O':
dfs(row-1,j)
for i in range(row):
for j in range(col):
if board[i][j]=='O':
board[i][j]='X'
if board[i][j]=='Z':
board[i][j]='O'
广度优先的写法也很简单,同上。
417. 太平洋大西洋水流问题
417. 太平洋大西洋水流问题
这题也是需要判断区域的四个边界,以此为判断能否流出两种河流的结果。
除此之外,该题的图内的值不可更改,所以需要另外创建visited去存储访问过的点,visited可以为图大小的二维数组,也可以为set集合或者list列表。
class Solution:
def pacificAtlantic(self, heights: List[List[int]]) -> List[List[int]]:
row = len(heights)
col = len(heights[0])
res = []
def dfs(i,j):
visited.add((i,j))
if i==0 or j==0:
nonlocal sign_pacific
sign_pacific = 1
if i==row-1 or j==col-1:
nonlocal sign_atlantic
sign_atlantic = 1
if sign_pacific and sign_atlantic:
return True
for x,y in (i+1, j),(i-1,j),(i,j+1),(i,j-1):
if 0<=x<row and 0<=y<col:
if heights[x][y]<=heights[i][j] and (x,y) not in visited:
dfs(x, y)
for i in range(row):
for j in range(col):
sign_pacific = 0
sign_atlantic = 0
# 不能改变原图的值,所以避免重复值,则需要新创建一个图
visited = set()
dfs(i,j)
if sign_pacific and sign_atlantic:
res.append([i,j])
return res
3.2、集合划分问题(等用于回溯的问题)
698. 划分为k个相等的子集
698. 划分为k个相等的子集
要划分相等子集,首先要判断能否划分,即能否被k整除,能的话再继续下一步判断。
k个子集相当于k个桶,将nums的物品依次丢入到这k个桶中去,每一个可能放可能不放复杂度为 O ( k n ) O(k^n) O(kn)相当于暴力搜索。
按序深搜每个物品放入每个桶中,能放入该桶,则深搜下一个物品,不能则回溯,放入下一个桶中。如果每个桶都不能放,则退出了k个桶的循环return False。
class Solution:
def canPartitionKSubsets(self, nums: List[int], k: int) -> bool:
target = sum(nums)
if target%k:
return False
target //=k
# 优化1,将nums物品按照从大道小排序,可减少搜搜复杂度。
# 如果物品大小大于背包,4个桶装不下,可以直接False
# 等于背包则直接放入而装满,进行下一个
nums.sort(reverse=True)
bucket = [0]*k
def dfs(ind):
if ind==len(nums):
return True
for i in range(k):
# 优化2,如果桶的大小相同,当放一个物品放不下时,放另一个相等大小的桶也一样放不下,则直接跳过不一样大小的桶进行dfs
if i>0 and bucket[i]==bucket[i-1]:
continue
# 优化3(这里没更改),if bucket[i]+nums[ind]<=target:再继续后面的
# 把 if bucket[i]<=target and dfs(ind+1): 拆开
bucket[i]+=nums[ind]
if bucket[i]<=target and dfs(ind+1):
return True
bucket[i]-=nums[ind]
return False
return dfs(0)
473. 火柴拼正方形
473. 火柴拼正方形
class Solution:
def makesquare(self, matchsticks: List[int]) -> bool:
target = sum(matchsticks)
if target%4:
return False
target //=4
bucket = [0]*4
matchsticks.sort(reverse=True)
def backtracking(ind):
if ind==len(matchsticks):
return True
for i in range(4):
if i>0 and bucket[i]==bucket[i-1]:
continue
bucket[i]+=matchsticks[ind]
if bucket[i]<=target and backtracking(ind+1):
return True
bucket[i]-=matchsticks[ind]
return False
return backtracking(0)
2305. 公平分发饼干
2305. 公平分发饼干
以cookies =[8,15,10,20,8]和k=2为例
相当于吧所有的方法找出来:
[61, 0]
[53, 8]
[41, 20]
[33, 28]
[51, 10]
[43, 18]
[31, 30]
[23, 38]
[46, 15]
[38, 23]
[26, 35]
[18, 43]
[36, 25]
[28, 33]
[16, 45]
[8, 53]
去找bucket里的最大值,整体的最小值:
res = min(res, max(bucket))
因为复杂度很高,再进行剪枝
import math
class Solution:
def distributeCookies(self, cookies: List[int], k: int) -> int:
# 因为可能无法均分,所以这里不去设置target值,而是设置一个变动的res
# res逐渐变小,但是是bucket里的最大值
# target = sum(cookies)
# target = math.ceil(target/k)
# 从最大值开始,找最小值,因为小就接近于均分
res = float('inf')
# 优化1
cookies.sort(reverse=True)
bucket = [0]*k
def backtracking(ind):
if ind==len(cookies):
# print(bucket)
nonlocal res
res = min(res, max(bucket))
return
for i in range(k):
# 优化2
if i>0 and bucket[i]==bucket[i-1]:
continue
# 优化3 剪枝,有桶大于res,直接去掉
if bucket[i]+cookies[ind]<res:
bucket[i]+=cookies[ind]
backtracking(ind+1)
bucket[i]-=cookies[ind]
backtracking(0)
return res

1723. 完成所有工作的最短时间
1723. 完成所有工作的最短时间
class Solution:
def minimumTimeRequired(self, jobs: List[int], k: int) -> int:
res = float('inf')
bucket = [0]*k
jobs.sort(reverse=True)
def backtracking(ind):
if ind==len(jobs):
nonlocal res
res = min(res, max(bucket))
return True
for i in range(k):
if i>0 and bucket[i]==bucket[i-1]:
continue
if bucket[i]+jobs[ind]<res:
bucket[i]+=jobs[ind]
backtracking(ind+1)
bucket[i]-=jobs[ind]
return False
backtracking(0)
return res
3.3、其他问题
547. 省份数量
547. 省份数量
这题是以一个表来展现相邻,这与岛的相邻不同,不能直接判表中的1相邻,实际上咱们每一行站在列的角度,行的列不相交,则不会直接相邻,可能间接相邻,需要深度搜索,若相交则一定相邻。当然这只是个思考判断方法,具体做题是另一种思路。
这里行与列一定相等,把坐标表示为城市名字。
遍历每一行,即从第一个城市开始探索与其相邻的城市,第一行是与0节点相连的所有其他城市,值为1则对其显示的列坐标城市,转到对应的行再进行深度搜索,寻找与其相邻的城市,重复该步骤,并且用visited进行存储,已经存在则无需重复再搜。
class Solution:
def findCircleNum(self, isConnected: List[List[int]]) -> int:
row = len(isConnected)
col = len(isConnected[0])
res = 0
def dfs(i):
visited.add(i)
for j in range(row):
if j not in visited and isConnected[i][j]==1:
dfs(j)
visited = set()
for i in range(row):
if i not in visited:
dfs(i)
res+=1
print(visited)
return res
深广搜问题相比回溯问题更加的简单,并且都有相似且固定的模板,相信你通过这篇文章,能对回溯与深广搜有了较为深刻的学习和认识!
参考
Fairly Nerdy
carlprogramming
