当前位置：首页 > article >正文

代码随想录刷题记录-27 图论 (4)拓扑排序

article 2025/1/15 12:59:24

一、拓扑排序精讲

题目：117. 软件构建

拓扑排序的背景

本题是拓扑排序的经典题目。

拓扑排序是经典的图论问题。

先说说拓扑排序的应用场景。

大学排课，例如先上A课，才能上B课，上了B课才能上C课，上了A课才能上D课，等等一系列这样的依赖顺序。问给规划出一条完整的上课顺序。

拓扑排序在文件处理上也有应用，我们在做项目安装文件包的时候，经常发现复杂的文件依赖关系， A依赖B，B依赖C，B依赖D，C依赖E 等等。

如果给出一条线性的依赖顺序来下载这些文件呢？

有录友想上面的例子都很简单啊，我一眼能给排序出来。

那如果上面的依赖关系是一百对呢，一千对甚至上万个依赖关系，这些依赖关系中可能还有循环依赖，你如何发现循环依赖呢，又如果排出线性顺序呢。

所以拓扑排序就是专门解决这类问题的。

概括来说，给出一个有向图，把这个有向图转成线性的排序就叫拓扑排序。

当然拓扑排序也要检测这个有向图是否有环，即存在循环依赖的情况，因为这种情况是不能做线性排序的。

所以拓扑排序也是图论中判断有向无环图的常用方法。

总结，拓扑排序应用于以下场景：

（1）处理依赖关系，把一个有向图转成线性的排序。

（2）判断有向无环图。

模拟过程

用本题的示例来模拟这一过程：

1、找到入度为0 的节点，加入结果集

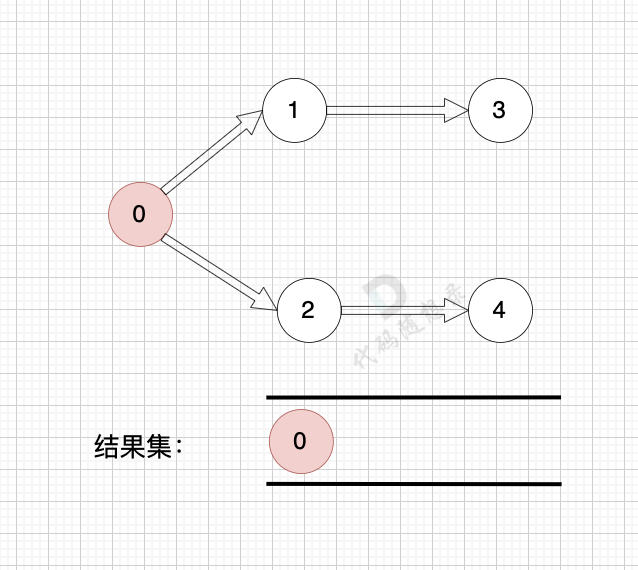
2、将该节点从图中移除

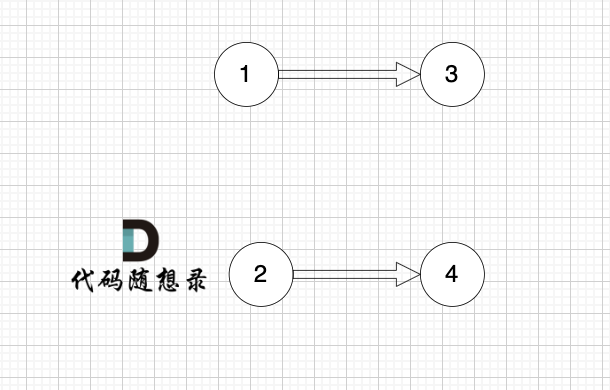
1、找到入度为0 的节点，加入结果集

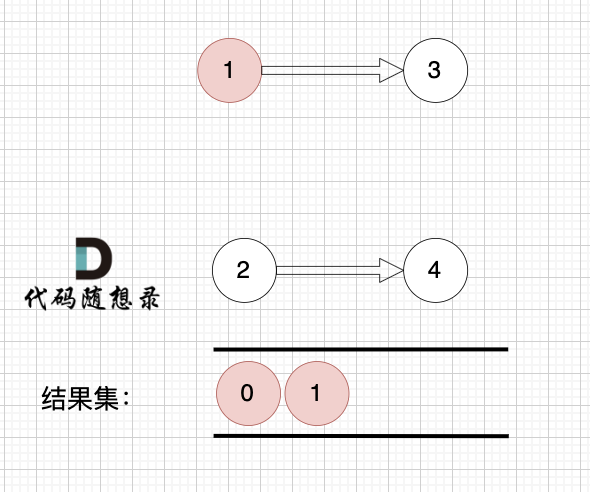
这里大家会发现，节点1 和节点2 入度都为0，选哪个呢？

选哪个都行，所以这也是为什么拓扑排序的结果是不唯一的。

2、将该节点从图中移除

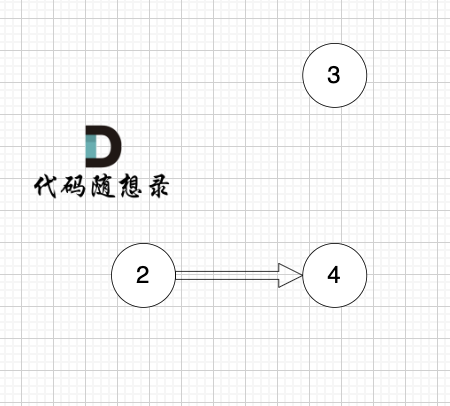
1、找到入度为0 的节点，加入结果集

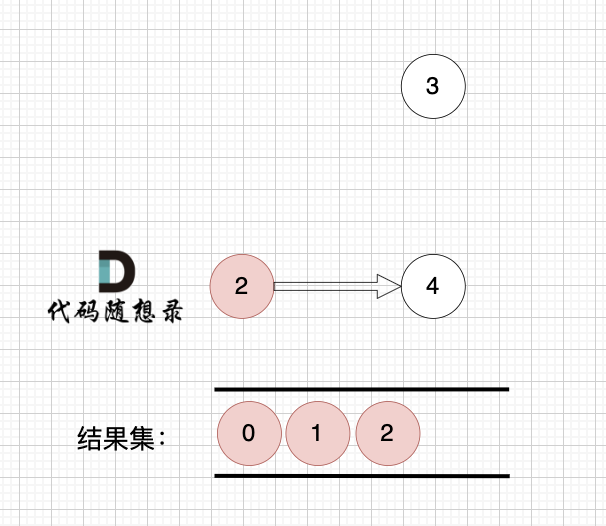
节点2 和节点3 入度都为0，选哪个都行，这里选节点2

2、将该节点从图中移除

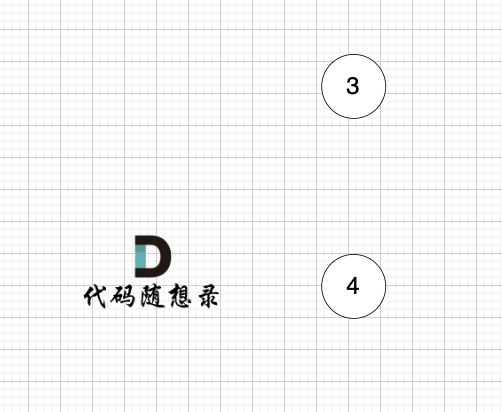
后面的过程一样的，节点3 和节点4，入度都为0，选哪个都行。

最后结果集为： 0 1 2 3 4 。当然结果不唯一的。

判断有环

如果有有向环怎么办呢？例如这个图：

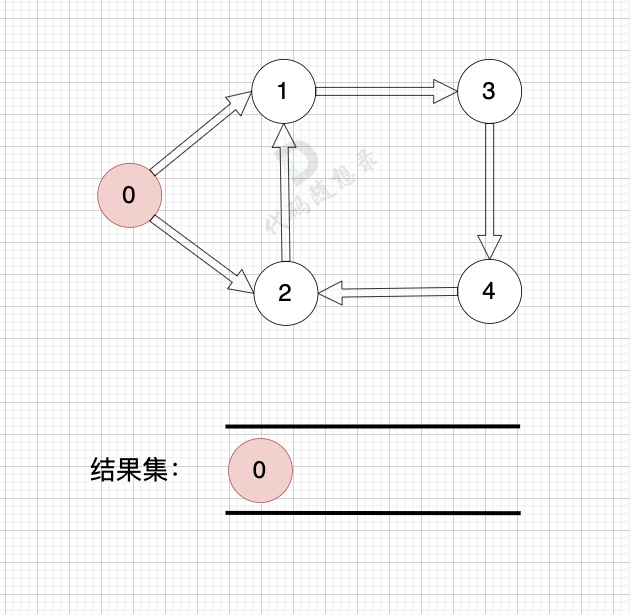
这个图，我们只能将入度为0 的节点0 接入结果集。

之后，节点1、2、3、4 形成了环，找不到入度为0 的节点了，所以此时结果集里只有一个元素。

那么如果我们发现结果集元素个数不等于图中节点个数，我们就可以认定图中一定有有向环。

这也是拓扑排序判断有向环的方法。

通过以上过程的模拟大家会发现这个拓扑排序好像不难，还有点简单。

写代码

理解思想后，确实不难，但代码写起来也不容易。

为了每次可以找到所有节点的入度信息，我们要在初始化的时候，就把每个节点的入度和每个节点的依赖关系做统计。

代码如下：

cin >> n >> m;
vector<int> inDegree(n, 0); // 记录每个文件的入度
vector<int> result; // 记录结果
unordered_map<int, vector<int>> umap; // 记录文件依赖关系

while (m--) {
    // s->t，先有s才能有t
    cin >> s >> t;
    inDegree[t]++; // t的入度加一
    umap[s].push_back(t); // 记录s指向哪些文件
}

找入度为0 的节点，我们需要用一个队列放存放。

因为每次寻找入度为0的节点，不一定只有一个节点，可能很多节点入度都为0，所以要将这些入度为0的节点放到队列里，依次去处理。

代码如下：


queue<int> que;
for (int i = 0; i < n; i++) {
    // 入度为0的节点，可以作为开头，先加入队列
    if (inDegree[i] == 0) que.push(i);
}

开始从队列里遍历入度为0 的节点，将其放入结果集。


while (que.size()) {
    int  cur = que.front(); // 当前选中的节点
    que.pop();
    result.push_back(cur);
    // 将该节点从图中移除 

}

这里面还有一个很重要的过程，如何把这个入度为0的节点从图中移除呢？

首先我们为什么要把节点从图中移除？

为的是将该节点作为出发点所连接的边删掉。

删掉的目的是什么呢？

要把该节点作为出发点所连接的节点的入度减一。

如果这里不理解，看上面的模拟过程第一步：

这事节点1 和节点2 的入度为 1。

将节点0删除后，图为这样：

那么节点0 作为出发点所连接的节点的入度就都做了减一的操作。

此时节点1 和节点 2 的入度都为0，这样才能作为下一轮选取的节点。

所以，我们在代码实现的过程中，本质是要将该节点作为出发点所连接的节点的入度减一就可以了，这样好能根据入度找下一个节点，不用真在图里把这个节点删掉。

该过程代码如下：


while (que.size()) {
    int  cur = que.front(); // 当前选中的节点
    que.pop();
    result.push_back(cur);
    // 将该节点从图中移除 
    vector<int> files = umap[cur]; //获取cur指向的节点
    if (files.size()) { // 如果cur有指向的节点
        for (int i = 0; i < files.size(); i++) { // 遍历cur指向的节点
            inDegree[files[i]] --; // cur指向的节点入度都做减一操作
            // 如果指向的节点减一之后，入度为0，说明是我们要选取的下一个节点，放入队列。
            if(inDegree[files[i]] == 0) que.push(files[i]); 
        }
    }

}

最后代码如下：

#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
using namespace std;
int main() {
    int m, n, s, t;
    cin >> n >> m;
    vector<int> inDegree(n, 0); // 记录每个文件的入度

    unordered_map<int, vector<int>> umap;// 记录文件依赖关系
    vector<int> result; // 记录结果

    while (m--) {
        // s->t，先有s才能有t
        cin >> s >> t;
        inDegree[t]++; // t的入度加一
        umap[s].push_back(t); // 记录s指向哪些文件
    }
    queue<int> que;
    for (int i = 0; i < n; i++) {
        // 入度为0的文件，可以作为开头，先加入队列
        if (inDegree[i] == 0) que.push(i);
        //cout << inDegree[i] << endl;
    }
    // int count = 0;
    while (que.size()) {
        int  cur = que.front(); // 当前选中的文件
        que.pop();
        //count++;
        result.push_back(cur);
        vector<int> files = umap[cur]; //获取该文件指向的文件
        if (files.size()) { // cur有后续文件
            for (int i = 0; i < files.size(); i++) {
                inDegree[files[i]] --; // cur的指向的文件入度-1
                if(inDegree[files[i]] == 0) que.push(files[i]);
            }
        }
    }
    if (result.size() == n) {
        for (int i = 0; i < n - 1; i++) cout << result[i] << " ";
        cout << result[n - 1];
    } else cout << -1 << endl;


}

本题的Java代码：

import java.util.*;
import java.util.List;


public class Main {

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        int[] inDegree = new int[n];
        Map<Integer,List<Integer>> map = new HashMap<>();
        for(int i = 0 ; i < n ; i++){
            map.put(i,new ArrayList<>());
        }
        for(int i = 0 ; i < m ; i++){
            int s = scanner.nextInt();
            int t = scanner.nextInt();
            inDegree[t]++;
            map.get(s).add(t);
        }
        Queue<Integer> queue = new ArrayDeque<>();
        for(int i = 0 ; i < n ; i++){
            if(inDegree[i] == 0){
                queue.add(i);
            }
        }
        List<Integer> result = new ArrayList<>();
        while(!queue.isEmpty()){
            int node = queue.remove();
            result.add(node);
            List<Integer> nextNodes = map.get(node);
            for(Integer nextNode : nextNodes){
                inDegree[nextNode]--;
                if(inDegree[nextNode] == 0){
                    queue.add(nextNode);
                }
            }
        }
        if(result.size() == n){
            for(int i = 0 ; i < result.size() - 1 ; i++){
                System.out.print(result.get(i) + " ");
            }
            System.out.println(result.get(result.size()-1));
        }else{
            System.out.println("-1");
        }


    }

}

注意本题的编号从0开始。

查看全文

http://www.kler.cn/a/289947.html