【AI】Pytorch_模型构建
建议点赞收藏关注!持续更新至pytorch大部分内容更完。
本文已达到10w字,故按模块拆开,详见目录导航。
整体框架如下
数据及预处理
模型及其构建
损失函数及优化器
本节目录
- 模型
- 线性回归
- 逻辑回归
- LeNet
- AlexNet
- 构建模块
- 组织复杂网络
- 初始化网络参数
- 梯度消失 or 梯度爆炸
- 定义网络层
- 卷积层
- 池化层
- 线性层(全连接层)
- 激活函数层
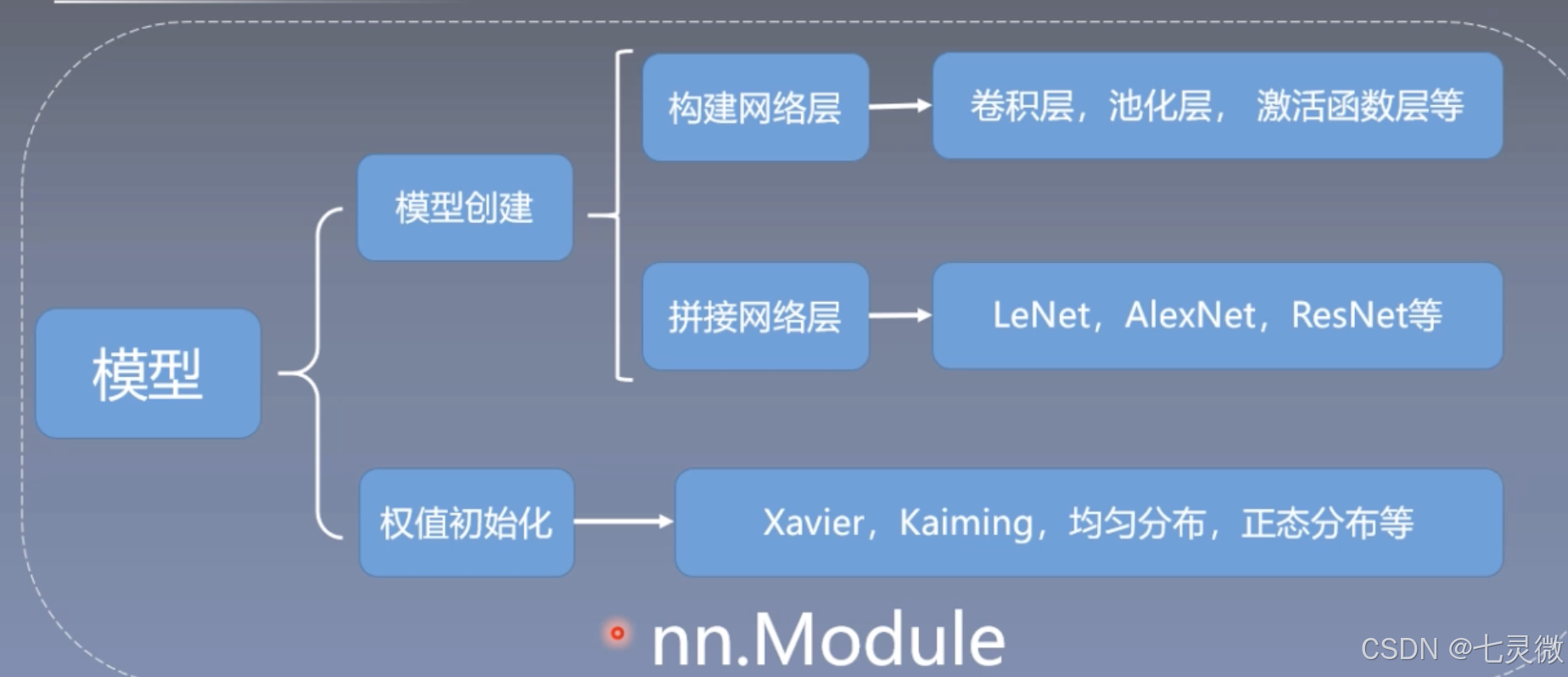
模型
模型训练基本步骤:数据->模型->损失函数->优化器->迭代训练
线性回归
1.确定模型:y=wx+b 关系是线性的,需要求解w,b
2.选择损失函数 MSE均方差

3.求解梯度并更新w,b
w=w-LRw.grad 加上梯度的负方向 即减梯度正方向
b=b-LRw.grad
# -*- coding:utf-8 -*-
"""
@brief : 一元线性回归模型
"""
import torch
import matplotlib.pyplot as plt
torch.manual_seed(10)
lr = 0.05 # 学习率
# 创建训练数据
x = torch.rand(20, 1) * 10 # x data (tensor), shape=(20, 1)
y = 2*x + (5 + torch.randn(20, 1)) # y data (tensor), shape=(20, 1)
#torch.randn(20, 1)是一些噪声
# 构建初始化线性回归参数
w = torch.randn((1), requires_grad=True)
b = torch.zeros((1), requires_grad=True)
for iteration in range(1000):
# 前向传播
wx = torch.mul(w, x)#w*x
y_pred = torch.add(wx, b)#y_pred是预测值=w*x+b
# 计算 MSE loss
loss = (0.5 * (y - y_pred) ** 2).mean()
#0.5这里是为了消掉求导中的系数2
# 反向传播 得到梯度
loss.backward()
# 更新参数 即减掉lr * grad梯度
b.data.sub_(lr * b.grad)
w.data.sub_(lr * w.grad)
# 清零张量的梯度 20191015增加
w.grad.zero_()
b.grad.zero_()
# 绘图
if iteration % 20 == 0:
plt.cla() # 防止社区版可视化时模型重叠
plt.scatter(x.data.numpy(), y.data.numpy())
plt.plot(x.data.numpy(), y_pred.data.numpy(), 'r-', lw=5)
plt.text(2, 20, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color': 'red'})
plt.xlim(1.5, 10)
plt.ylim(8, 28)
plt.title("Iteration: {}\nw: {} b: {}".format(iteration, w.data.numpy(), b.data.numpy()))
plt.pause(0.5)
if loss.data.numpy() < 1:#loss小于1时停止迭代
break
plt.show()
逻辑回归
注意:是线性的二分类模型
模型表达式:y=f(wx+b), f(x)=1/(1+e^-x),f(x)成为sigmoid函数 又叫logistic函数,它会将输入的数据映射到0~1之间(概率)

如何二分类?通常将阈值设置为0.5,超过0.5为1,不足0.5为0

逻辑回归又名 对数几率回归,这里的几率对应y/(1-y)
ln[y/(1-y)]=wx+b 公式与逻辑回归表达式可以互相得到
对数回归:表达式lny=wx+b
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
torch.manual_seed(10)
# ============================ step 1/5 生成数据 ============================
sample_nums = 100
mean_value = 1.7
bias = 1
n_data = torch.ones(sample_nums, 2)
x0 = torch.normal(mean_value * n_data, 1) + bias # 类别0 数据 shape=(100, 2)
#normal(mean,std)
y0 = torch.zeros(sample_nums) # 类别0 标签 shape=(100)
x1 = torch.normal(-mean_value * n_data, 1) + bias # 类别1 数据 shape=(100, 2)
y1 = torch.ones(sample_nums) # 类别1 标签 shape=(100)
train_x = torch.cat((x0, x1), 0)
train_y = torch.cat((y0, y1), 0)
# ============================ step 2/5 选择模型 ============================
class LR(nn.Module):
def __init__(self):
super(LR, self).__init__()
self.features = nn.Linear(2, 1)
self.sigmoid = nn.Sigmoid()
def forward(self, x):#前向传播
x = self.features(x)
x = self.sigmoid(x)
return x
lr_net = LR() # 实例化逻辑回归模型
# ============================ step 3/5 选择损失函数 ============================
loss_fn = nn.BCELoss()#二分类交叉熵
# ============================ step 4/5 选择优化器 ============================
lr = 0.01 # 学习率
optimizer = torch.optim.SGD(lr_net.parameters(), lr=lr, momentum=0.9)
#SGD随机梯度下降法
'''
关于momentum
SGD(Stochastic Gradient Descent,随机梯度下降)是一种常用的优化算法,用于训练机器学习模型。 Momentum 是SGD的一种变体,它引入了一个动量项(momentum term),目的是为了加速收敛并减少震荡。简单来说,Momentum会在每一次更新方向上考虑历史的梯度信息,而不是仅仅基于当前的梯度。
这个动量项会让模型偏向于沿之前梯度的方向移动,如果之前的方向是有利的,那么在后续迭代中会保持这种趋势,有助于避免陷入局部最优。
'''
# ============================ step 5/5 模型训练 ============================
for iteration in range(1000):
# 前向传播:将数据输入给模型
y_pred = lr_net(train_x)
# 计算 loss
loss = loss_fn(y_pred.squeeze(), train_y)
# 反向传播
loss.backward()
# 更新参数
optimizer.step()
# 清空梯度
optimizer.zero_grad()
# 绘图
if iteration % 20 == 0:
mask = y_pred.ge(0.5).float().squeeze() # 以0.5为阈值进行分类
correct = (mask == train_y).sum() # 计算正确预测的样本个数
acc = correct.item() / train_y.size(0) # 计算分类准确率
plt.scatter(x0.data.numpy()[:, 0], x0.data.numpy()[:, 1], c='r', label='class 0')
plt.scatter(x1.data.numpy()[:, 0], x1.data.numpy()[:, 1], c='b', label='class 1')
w0, w1 = lr_net.features.weight[0]
w0, w1 = float(w0.item()), float(w1.item())
plot_b = float(lr_net.features.bias[0].item())
plot_x = np.arange(-6, 6, 0.1)
plot_y = (-w0 * plot_x - plot_b) / w1
plt.xlim(-5, 7)
plt.ylim(-7, 7)
plt.plot(plot_x, plot_y)
plt.text(-5, 5, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color': 'red'})
plt.title("Iteration: {}\nw0:{:.2f} w1:{:.2f} b: {:.2f} accuracy:{:.2%}".format(iteration, w0, w1, plot_b, acc))
plt.legend()
plt.show()
plt.pause(0.5)
if acc > 0.99:
break
LeNet
conv1->pool1->conv2->pool2->fc1->fc2->fc3

forward:从左往右的顺序,前向传播;反之为backward
AlexNet


features部分是卷积池化
classfier部分是全联接
Alexnet是分组卷积,原因是受制于硬件,因为它用了两个GPU进行训练。如上图结构所示,一张图片分成上下两组卷积进行,直到最后全连接时上下两组才连接起来。
class AlexNet(nn.Module):
def __init__(self, num_classes: int = 1000, dropout: float = 0.5) -> None:
super().__init__()
_log_api_usage_once(self)
self.features = nn.Sequential(
nn.Conv2d(3, 64, kernel_size=11, stride=4, padding=2),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Conv2d(64, 192, kernel_size=5, padding=2),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Conv2d(192, 384, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(384, 256, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(256, 256, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2),
)
self.avgpool = nn.AdaptiveAvgPool2d((6, 6))
self.classifier = nn.Sequential(
nn.Dropout(p=dropout),
nn.Linear(256 * 6 * 6, 4096),#全连接
nn.ReLU(inplace=True),
nn.Dropout(p=dropout),
nn.Linear(4096, 4096),
nn.ReLU(inplace=True),
nn.Linear(4096, num_classes),
)
def forward(self, x: torch.Tensor) -> torch.Tensor:
x = self.features(x)
x = self.avgpool(x)
x = torch.flatten(x, 1)
x = self.classifier(x)
return x
# 4 AlexNet
alexnet = torchvision.models.AlexNet()
构建模块
构建模块需要构建子模块(在__init__()),拼接子模块(在forward())。
所有的模型、网络层都是继承nn.Module

nn.Module总结:
- 一个module可以包含多个子module,比如说convNd,pool都是一个module,区别在于这种子module的module属性为空,即它们没有子模块了
- 一个module相当于一个运算,必须实现forward()
- 每个module都有8个字典管理它的属性;例如,执行module的init创建self.conv2时就会进入__setattr__判断传参类型,如果是parameter则加入到parameters字典中,其key==[该参数],如果是module则加入到modules字典中,其key==[conv2];(细节可以通过源码debug来查看)
nn.Module的属性有

以下是与hooks有关的字典:

class LeNet(nn.Module):
def __init__(self, classes):
super(LeNet, self).__init__()#这里实现了调用父类的init()
self.conv1 = nn.Conv2d(3, 6, 5)
#这些都可以debug之后step in 看一下它继续往哪个代码底层执行,了解代码原理
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16*5*5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, classes)
def forward(self, x):
out = F.relu(self.conv1(x))
out = F.max_pool2d(out, 2)
out = F.relu(self.conv2(out))
out = F.max_pool2d(out, 2)
out = out.view(out.size(0), -1)
out = F.relu(self.fc1(out))
out = F.relu(self.fc2(out))
out = self.fc3(out)
return out
def initialize_weights(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.xavier_normal_(m.weight.data)
if m.bias is not None:
m.bias.data.zero_()
elif isinstance(m, nn.BatchNorm2d):
m.weight.data.fill_(1)
m.bias.data.zero_()
elif isinstance(m, nn.Linear):
nn.init.normal_(m.weight.data, 0, 0.1)
m.bias.data.zero_()
# -*- coding: utf-8 -*-
"""
# @file name : create_module.py
# @brief : 学习模型创建学习
"""
import os
BASE_DIR = os.path.dirname(os.path.abspath(__file__))
import numpy as np
import torch
import torch.nn as nn
from torch.utils.data import DataLoader
import torchvision.transforms as transforms
import torch.optim as optim
from matplotlib import pyplot as plt
path_lenet = os.path.abspath(os.path.join(BASE_DIR, "..", "..", "model", "lenet.py"))
path_tools = os.path.abspath(os.path.join(BASE_DIR, "..", "..", "tools", "common_tools.py"))
assert os.path.exists(path_lenet), "{}不存在,请将lenet.py文件放到 {}".format(path_lenet, os.path.dirname(path_lenet))
assert os.path.exists(path_tools), "{}不存在,请将common_tools.py文件放到 {}".format(path_tools, os.path.dirname(path_tools))
import sys
hello_pytorch_DIR = os.path.abspath(os.path.dirname(__file__)+os.path.sep+".."+os.path.sep+"..")
sys.path.append(hello_pytorch_DIR)
from model.lenet import LeNet
from tools.my_dataset import RMBDataset
from tools.common_tools import set_seed
set_seed() # 设置随机种子
rmb_label = {"1": 0, "100": 1}
# 参数设置
MAX_EPOCH = 10
BATCH_SIZE = 16
LR = 0.01
log_interval = 10
val_interval = 1
# ============================ step 1/5 数据 ============================
split_dir = os.path.abspath(os.path.join(BASE_DIR, "..", "..", "data", "rmb_split"))
if not os.path.exists(split_dir):
raise Exception(r"数据 {} 不存在, 回到lesson-06\1_split_dataset.py生成数据".format(split_dir))
train_dir = os.path.join(split_dir, "train")
valid_dir = os.path.join(split_dir, "valid")
norm_mean = [0.485, 0.456, 0.406]
norm_std = [0.229, 0.224, 0.225]
train_transform = transforms.Compose([
transforms.Resize((32, 32)),
transforms.RandomCrop(32, padding=4),
transforms.ToTensor(),
transforms.Normalize(norm_mean, norm_std),
])
valid_transform = transforms.Compose([
transforms.Resize((32, 32)),
transforms.ToTensor(),
transforms.Normalize(norm_mean, norm_std),
])
# 构建MyDataset实例
train_data = RMBDataset(data_dir=train_dir, transform=train_transform)
valid_data = RMBDataset(data_dir=valid_dir, transform=valid_transform)
# 构建DataLoder
train_loader = DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)
valid_loader = DataLoader(dataset=valid_data, batch_size=BATCH_SIZE)
# ============================ step 2/5 模型 ============================
net = LeNet(classes=2)
net.initialize_weights()
# ============================ step 3/5 损失函数 ============================
criterion = nn.CrossEntropyLoss() # 选择损失函数
# ============================ step 4/5 优化器 ============================
optimizer = optim.SGD(net.parameters(), lr=LR, momentum=0.9) # 选择优化器
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=10, gamma=0.1) # 设置学习率下降策略
# ============================ step 5/5 训练 ============================
train_curve = list()
valid_curve = list()
for epoch in range(MAX_EPOCH):
loss_mean = 0.
correct = 0.
total = 0.
net.train()
for i, data in enumerate(train_loader):
# forward
inputs, labels = data
outputs = net(inputs)
# backward
optimizer.zero_grad()
loss = criterion(outputs, labels)
loss.backward()
# update weights
optimizer.step()
# 统计分类情况
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).squeeze().sum().numpy()
# 打印训练信息
loss_mean += loss.item()
train_curve.append(loss.item())
if (i+1) % log_interval == 0:
loss_mean = loss_mean / log_interval
print("Training:Epoch[{:0>3}/{:0>3}] Iteration[{:0>3}/{:0>3}] Loss: {:.4f} Acc:{:.2%}".format(
epoch, MAX_EPOCH, i+1, len(train_loader), loss_mean, correct / total))
loss_mean = 0.
scheduler.step() # 更新学习率
# validate the model
if (epoch+1) % val_interval == 0:
correct_val = 0.
total_val = 0.
loss_val = 0.
net.eval()
with torch.no_grad():
for j, data in enumerate(valid_loader):
inputs, labels = data
outputs = net(inputs)
loss = criterion(outputs, labels)
_, predicted = torch.max(outputs.data, 1)
total_val += labels.size(0)
correct_val += (predicted == labels).squeeze().sum().numpy()
loss_val += loss.item()
valid_curve.append(loss_val)
print("Valid:\t Epoch[{:0>3}/{:0>3}] Iteration[{:0>3}/{:0>3}] Loss: {:.4f} Acc:{:.2%}".format(
epoch, MAX_EPOCH, j+1, len(valid_loader), loss_val, correct / total))
train_x = range(len(train_curve))
train_y = train_curve
train_iters = len(train_loader)
valid_x = np.arange(1, len(valid_curve)+1) * train_iters*val_interval # 由于valid中记录的是epochloss,需要对记录点进行转换到iterations
valid_y = valid_curve
plt.plot(train_x, train_y, label='Train')
plt.plot(valid_x, valid_y, label='Valid')
plt.legend(loc='upper right')
plt.ylabel('loss value')
plt.xlabel('Iteration')
plt.show()
# ============================ inference ============================
BASE_DIR = os.path.dirname(os.path.abspath(__file__))
test_dir = os.path.join(BASE_DIR, "test_data")
test_data = RMBDataset(data_dir=test_dir, transform=valid_transform)
valid_loader = DataLoader(dataset=test_data, batch_size=1)
for i, data in enumerate(valid_loader):
# forward
inputs, labels = data
outputs = net(inputs)
_, predicted = torch.max(outputs.data, 1)
rmb = 1 if predicted.numpy()[0] == 0 else 100
print("模型获得{}元".format(rmb))
组织复杂网络
介绍容器containers,包装起来作为一个整体

可以利用sequential将LeNet划分成features,classifier两部分

可以发现sequential定义后的打印出来模型结构,里面不再是有name的,而是拿序号区分不同层的。所以要用字典形式构建,见下面代码中class LeNetSequential 和class LeNetSequentialOrderDict的区别。





# -*- coding: utf-8 -*-
"""
# @file name : module_containers.py
# @brief : 模型容器——Sequential, ModuleList, ModuleDict
"""
import torch
import torchvision
import torch.nn as nn
from collections import OrderedDict
# ============================ Sequential
class LeNetSequential(nn.Module):
def __init__(self, classes):
super(LeNetSequential, self).__init__()
self.features = nn.Sequential(
nn.Conv2d(3, 6, 5),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, 5),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2),)
self.classifier = nn.Sequential(
nn.Linear(16*5*5, 120),
nn.ReLU(),
nn.Linear(120, 84),
nn.ReLU(),
nn.Linear(84, classes),)
def forward(self, x):
x = self.features(x)#自己定义的sequential
x = x.view(x.size()[0], -1)
x = self.classifier(x)#自己定义的sequential
return x
class LeNetSequentialOrderDict(nn.Module):
def __init__(self, classes):
super(LeNetSequentialOrderDict, self).__init__()
self.features = nn.Sequential(OrderedDict({
'conv1': nn.Conv2d(3, 6, 5),
'relu1': nn.ReLU(inplace=True),
'pool1': nn.MaxPool2d(kernel_size=2, stride=2),
'conv2': nn.Conv2d(6, 16, 5),
'relu2': nn.ReLU(inplace=True),
'pool2': nn.MaxPool2d(kernel_size=2, stride=2),
}))
self.classifier = nn.Sequential(OrderedDict({
'fc1': nn.Linear(16*5*5, 120),
'relu3': nn.ReLU(),
'fc2': nn.Linear(120, 84),
'relu4': nn.ReLU(inplace=True),
'fc3': nn.Linear(84, classes),
}))
def forward(self, x):
x = self.features(x)
x = x.view(x.size()[0], -1)
x = self.classifier(x)
return x
# net = LeNetSequential(classes=2)
# net = LeNetSequentialOrderDict(classes=2)
#
# fake_img = torch.randn((4, 3, 32, 32), dtype=torch.float32)
#
# output = net(fake_img)
#
# print(net)
# print(output)
# ============================ ModuleList
class ModuleList(nn.Module):
def __init__(self):
super(ModuleList, self).__init__()
self.linears = nn.ModuleList([nn.Linear(10, 10) for i in range(20)])# # 输入特征数为10,输出特征数为10
def forward(self, x):
for i, linear in enumerate(self.linears):
x = linear(x)
return x
# net = ModuleList()
#
# print(net)
#
# fake_data = torch.ones((10, 10))
#
# output = net(fake_data)
#
# print(output)
# ============================ ModuleDict
class ModuleDict(nn.Module):
def __init__(self):
super(ModuleDict, self).__init__()
self.choices = nn.ModuleDict({
'conv': nn.Conv2d(10, 10, 3),
'pool': nn.MaxPool2d(3)
})
self.activations = nn.ModuleDict({
'relu': nn.ReLU(),
'prelu': nn.PReLU()
})
def forward(self, x, choice, act):
x = self.choices[choice](x)
x = self.activations[act](x)
return x
net = ModuleDict()
fake_img = torch.randn((4, 10, 32, 32))
output = net(fake_img, 'conv', 'relu')
print(output)
# 4 AlexNet
alexnet = torchvision.models.AlexNet()
初始化网络参数
梯度消失 or 梯度爆炸
消失原因:深层网络;不合适的损失函数
爆炸原因:权值初始化过大
解决方法:梯度剪切、权重正则化、激活函数改进、使用batchnorm、ResNet
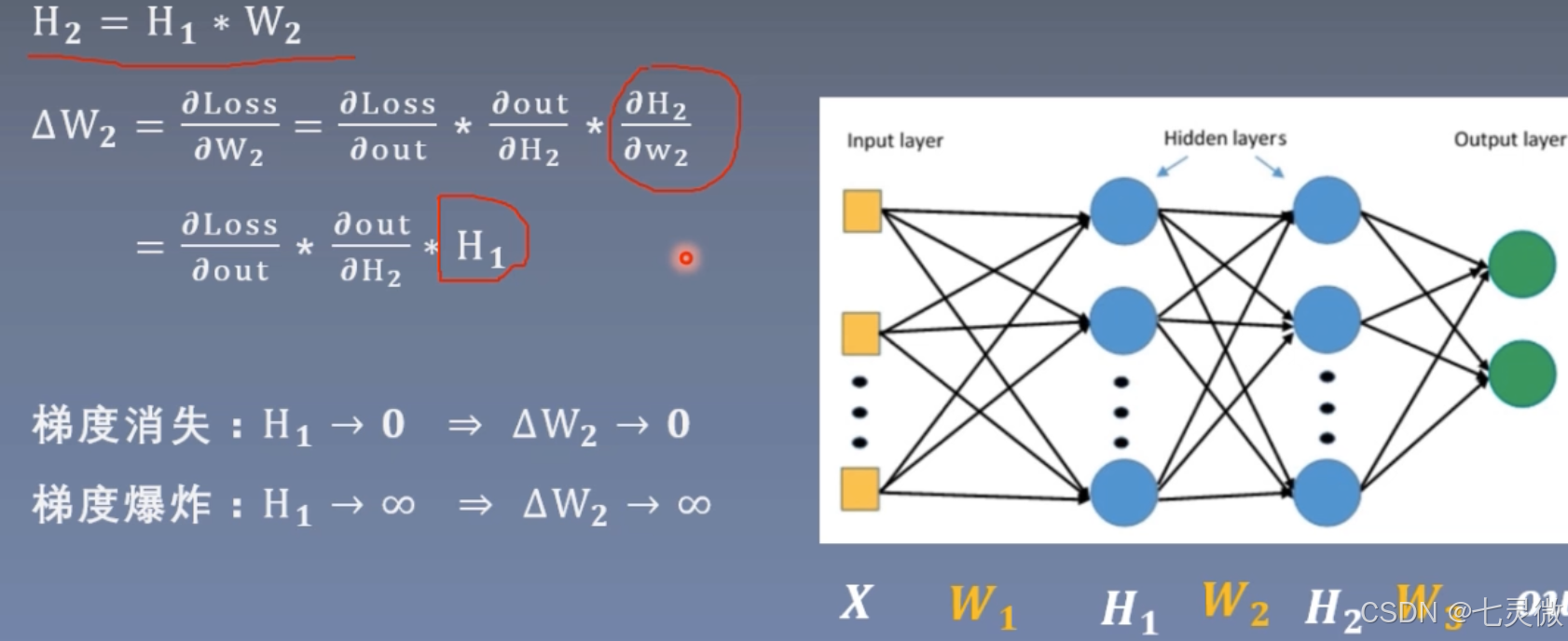
也就是说要控制网络层每一层输出不能太大,也不能太小。也就是说数据的方差不能过大过小,维持在1即可。

证明如下



红色圈起来的部分就是 想要让每次标准差std都稳定在1(左右),已知初始化D(xi)=1,则需要D(w)=1/n即可
通常Xavier 泽威尔采用均匀分布,如下图右边所示。

n_i是输入层的神经元个数,n_(i+1)是输出层的神经元个数。
当需要保持方差一致性(始终在1左右),则有上图公式推导。

这里的a是负半轴的斜率,第二行是变种relu
"""
总结 这里首先初始化标准差为1,后面在31层就会变成nan
# @file name : grad_vanish_explod.py
# @brief : 梯度消失与爆炸实验
"""
import os
import torch
import random
import numpy as np
import torch.nn as nn
from tools.common_tools import set_seed
set_seed(1) # 设置随机种子
class MLP(nn.Module):
def __init__(self, neural_num, layers):
super(MLP, self).__init__()
#构建100层线性层,每层有256个神经元
self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
self.neural_num = neural_num
def forward(self, x):
for (i, linear) in enumerate(self.linears):
x = linear(x)
#xavier x=torch.tanh(x)
#后面relu非饱和激活函数替换掉了饱和函数tanh等,用kaiming初始化替换掉对应的xavier初始化
x = torch.relu(x)
print("layer:{}, std:{}".format(i, x.std()))
#判断是否为nan
if torch.isnan(x.std()):
print("output is nan in {} layers".format(i))
break
return x
def initialize(self):
#遍历每一个模块modules
for m in self.modules():
if isinstance(m, nn.Linear):#判断模块是否为线性层
##初始值为标准正态分布,均值为0,标准差为1,但是每层的标准差会越来越大,发生std爆炸
nn.init.normal_(m.weight.data) #标准正态分布进行初始化
#均值为0,标准差为1,标准差会发生爆炸
#此时的初始化权值可以使每层的均值为0,std为1.
nn.init.normal_(m.weight.data, std=np.sqrt(1/self.neural_num))
#手动计算 Xavier
# a = np.sqrt(6 / (self.neural_num + self.neural_num))
'''
计算激活函数的增益,
即增益值是指张量的数据输入到激活函数之后标准差的变化上下限的绝对值。
例如对于0均值,1标准差的数据而言,经过激活函数tanh之后,标准差会减少5/3倍左右,如果对与经过激活函数后的数据进行增益变换(一般来说是乘上增益系数),可以使当前模块和激活函数连续作用后的输出张量元素分布服从一个比较合理的值。
'''
# tanh_gain = nn.init.calculate_gain('tanh')
# a *= tanh_gain
#设置均匀分布来初始化权值
# nn.init.uniform_(m.weight.data, -a, a)
#自动计算
nn.init.xavier_uniform_(m.weight.data, gain=nn.init.calculate_gain('tanh'))
#手动计算 这个是kaiming初始化,此时a==0
# nn.init.normal_(m.weight.data, std=np.sqrt(2 / self.neural_num))
#自动计算
nn.init.kaiming_normal_(m.weight.data)
flag = 0
# flag = 1
if flag:
layer_nums = 100 #100层神经网络
neural_nums = 256 #每一层神经元个数为256
batch_size = 16
net = MLP(neural_nums, layer_nums)
net.initialize() #初始化weight.data
inputs = torch.randn((batch_size, neural_nums)) # 输入数据设置为标准正态分布normal: mean=0, std=1
output = net(inputs)
print(output)
# ======================================= calculate gain =======================================
# flag = 0
flag = 1
if flag:
x = torch.randn(10000) #标准正态分布创建10000个数据点
out = torch.tanh(x)
gain = x.std() / out.std() #gain是一个变化比例 输入数据的标准差/输出数据的标准差
print('gain:{}'.format(gain))
tanh_gain = nn.init.calculate_gain('tanh')
print('tanh_gain in PyTorch:', tanh_gain)

nn.init.calculate_gain(nonlinearity,param=None)
'''
计算激活函数方差变化尺度 =输入数据的方差/经过激活函数后输出数据的方差
nonlinearity:激活函数名称
param:激活函数参数 如Leaky ReLU的Negative_slop
'''
定义网络层
卷积层



下图是一个三维卷积:利用二维卷积在一张图片的3个通道上进行,最后叠加起来。

padding:可以利用它保持特征图shape不变
dilation:空洞卷积
尺寸计算:


torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)
'''
(1)功能:对多个二维信号进行二维卷积;
(2)参数:
in_channels: 输入通道数;
out_channels: 输出通道数,等于卷积核的个数;
kernel_size: 卷积核的尺寸;
stride: 步长,stride步长是滑动时两个维度都一同滑动几个像素;
padding: 填充个数,保证输入和输出图像在尺寸上是匹配的;
dilation: 空洞卷积的大小;
groups: 分组卷积设置;
bias: 偏置;
'''
set_seed(3) # 设置随机种子 随机种子不一样,之后nn.init.xavier_normal_初始化也不一样,导致图片卷积后的效果不同。
# ================================= load img ==================================
path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), "lena.png")
img = Image.open(path_img).convert('RGB') # 0~255 RGB
# convert to tensor 张量
img_transform = transforms.Compose([transforms.ToTensor()])
img_tensor = img_transform(img)
# C*H*W to B*C*H*W 扩展成四维,增加batchsize维度
img_tensor.unsqueeze_(dim=0)
# ================================= create convolution layer ==================================
# ================ 2d
flag = 1
# flag = 0
if flag:
#图像是RGB具有三个通道,因此in_channels=3,设置一个卷积核来观察out_channels=1,卷积核为3*3
conv_layer = nn.Conv2d(3, 1, 3) # (in_channels, out_channels, 卷积核size)
#打印可以发现conv2d的_parameters字典中的weight.shape为[1,3,3,3]
#=(out_channels, in_channels , h, w) h,w是二维卷积核的尺寸
nn.init.xavier_normal_(conv_layer.weight.data)#初始化
# calculation
img_conv = conv_layer(img_tensor)
# ================================= visualization ==================================
print("卷积前尺寸:{}\n卷积后尺寸:{}".format(img_tensor.shape, img_conv.shape))
img_conv = transform_invert(img_conv[0, 0:1, ...], img_transform)
img_raw = transform_invert(img_tensor.squeeze(), img_transform)
plt.subplot(122).imshow(img_conv, cmap='gray')
plt.subplot(121).imshow(img_raw)
plt.show()
转置卷积(常用于图像分割)
但最好不要称其为反卷积,因为卷积与其是不可逆的运算,虽然前后图像相转置的,但是权值不可逆。

假设图像shape 44, kernel 33, padding=0,stride=1
正常卷积:首先,将输入图像44拉成161的向量,其中16是44所有的像素;1是1张图片。
然后,卷积核33会变成416的矩阵,其中16是33=9个权值通过补0得到16个数;,4是根据图像尺寸、padding、stride、dilation等计算得到的输出图像中像素的总个数。
最后,卷积核矩阵乘以图像矩阵得到41,然后再reshape为22的输出特征图。
转置卷积:就是在正常卷积之后22 再转置回去44
首先,将输入图像22拉成41的向量,其中4是22=4得到的输入图像中所有像素的个数,1是1张图片。
然后,卷积核33会变成164的矩阵,其中4是33=9中剔除多余的剩下的4个,16是根据图像尺寸、padding、stride、dilation等计算得到的输出图像中像素的总个数。
最后,卷积核矩阵乘以图像矩阵得到161,然后再reshape为44的输出特征图。


尺寸计算公式刚好和卷积是相逆的。
反卷积过后会有棋盘效应,可以看到处理后图像像棋盘一样。

nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1, padding_mode='zeros', device=None, dtype=None)
'''
参数同卷积参数
'''
# -*- coding: utf-8 -*-
"""
# @file name : nn_layers_convolution.py
# @brief : 学习卷积层
"""
import os
import torch.nn as nn
from PIL import Image
from torchvision import transforms
from matplotlib import pyplot as plt
from tools.common_tools import transform_invert, set_seed
set_seed(3) # 设置随机种子
# ================================= load img ==================================
path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), "lena.png")
img = Image.open(path_img).convert('RGB') # 0~255 RGB
# convert to tensor 张量
img_transform = transforms.Compose([transforms.ToTensor()])
img_tensor = img_transform(img)
# C*H*W to B*C*H*W 扩展成四维,增加batchsize维度
img_tensor.unsqueeze_(dim=0)
# ================================= create convolution layer ==================================
# ================ 2d
flag = 1
# flag = 0
if flag:
#图像是RGB具有三个通道,因此in_channels=3,设置一个卷积核来观察out_channels=1,卷积核为3*3
conv_layer = nn.Conv2d(3, 1, 3) # (in_channels, out_channels, 卷积核size)
#初始化
#weights:[1,3,3,3]=(out_channels, in_channels , h, w) h,w是二维卷积核的尺寸
nn.init.xavier_normal_(conv_layer.weight.data)
# calculation
img_conv = conv_layer(img_tensor)
# ================ transposed
# flag = 1
flag = 0
if flag:
conv_layer = nn.ConvTranspose2d(3, 1, 3, stride=2) #(in_channels, out_channels, 卷积核size)
nn.init.xavier_normal_(conv_layer.weight.data)
# calculation
img_conv = conv_layer(img_tensor)
# ================================= visualization ==================================
print("卷积前尺寸:{}\n卷积后尺寸:{}".format(img_tensor.shape, img_conv.shape))
img_conv = transform_invert(img_conv[0, 0:1, ...], img_transform)
img_raw = transform_invert(img_tensor.squeeze(), img_transform)
plt.subplot(122).imshow(img_conv, cmap='gray')
plt.subplot(121).imshow(img_raw)
plt.show()
2d卷积一般用于图片,3d卷积一般用于视频,当做3d卷积时,需要在原先shape中间插入一个D-deep,作为图片帧数
img_tensor.unsqueeze_(dim=2) # B*C*H*W to B*C*D*H*W
conv_layer = nn.Conv3d(3, 1, (3, 3, 3), padding=(1, 0, 0), bias=False)#(3,3,3)分别表示deep方向的kernel大小,shape
'''
如果padding[0]不为1的话,
则deep方向上只有原图片,但是原图片的shape转变成
1*3*1*512*512,batchsize*channel*deep*height*width
显然 图片shape的deep方向1<kernel deep方向的3 程序会报错
当padding[0]为1的话,相当于在原图像前后各添加一层0,这样就3 >=kernel的deep方向3,就不会报错了
'''
3d卷积是在三个方向上卷积

池化层
对信号收集总结,使数量多到少,有maxpool/avgpool
nn.MaxPool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)
'''
kernel_size: 池化核的尺寸;
stride: 步长,stride步长是滑动时滑动几个像素;通常与kernel_size一致,不会去重叠。
padding: 填充个数,保证输入和输出图像在尺寸上是匹配的;
dilation: 空洞卷积的大小;
ceil_mode:尺寸取整,ceil_mode设置为True则为尺寸向上取整,默认为False即尺寸向下取整;
return_indices:记录最大值像素所在的位置的索引,通常用于最大值反池化上采样时使用;
'''
set_seed(1) # 设置随机种子
# ================================= load img ==================================
path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), "lena.png")
img = Image.open(path_img).convert('RGB') # 0~255
# convert to tensor
#c:通道,h:高,w:宽
img_transform = transforms.Compose([transforms.ToTensor()])
img_tensor = img_transform(img)
img_tensor.unsqueeze_(dim=0) # C*H*W to B*C*H*W
# ================================= create convolution layer ==================================
# ================ maxpool
flag = 1
if flag:
#stride步长通常与池化窗口大小2*2一致,保证池化时不会发生重叠
maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2))
img_pool = maxpool_layer(img_tensor)
# ================================= visualization ==================================
print("池化前尺寸:{}\n池化后尺寸:{}".format(img_tensor.shape, img_pool.shape))
img_pool = transform_invert(img_pool[0, 0:3, ...], img_transform)
img_raw = transform_invert(img_tensor.squeeze(), img_transform)
plt.subplot(122).imshow(img_pool)
plt.subplot(121).imshow(img_raw)
plt.show()
池化后照片没有啥区别,所以 池化常用于冗余信息的剔除并减少计算量。
最大值反池化就是利用return_indices将原先池化后的元素放到新区域的对应索引上,其他区域为0

nn.MaxUnpool2d(kernel_size, stride=None, padding=0)
nn.AvgPool2d(kernel_size, stride=None, padding=0, ceil_mode=False, count_include_pad=True, divisor_override=None)
'''
ceil_mode:尺寸取整,ceil_mode设置为True则为尺寸向上取整,默认为False即尺寸向下取整;
count_include_pad:填充值是否用于计算;
divisor_override:除法因子,此时计算平均值时分母为divisor_override,本来是像素值的个数。
平均值池化的图像相较于最大值池化的图像较暗淡,
(像素越大越亮 偏白)
因为像素值较小,最大值池化图像取得是最大值,
平均值池化图像取得是平均值。
'''
set_seed(1) # 设置随机种子
# ================================= load img ==================================
path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), "lena.png")
img = Image.open(path_img).convert('RGB') # 0~255
# convert to tensor
#c:通道,h:高,w:宽
img_transform = transforms.Compose([transforms.ToTensor()])
img_tensor = img_transform(img)
img_tensor.unsqueeze_(dim=0) # C*H*W to B*C*H*W
# ================================= create convolution layer ==================================
# ================ max unpool
flag = 1
if flag:
# pooling
img_tensor = torch.randint(high=5, size=(1, 1, 4, 4), dtype=torch.float) #生成尺寸为1*1*4*4的整数[0, 5)均匀分布
maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2), return_indices=True)
img_pool, indices = maxpool_layer(img_tensor) #记录最大像素值的索引
# unpooling
#创建反池化层的输入,输入的尺寸与图片池化后的尺寸一致。
img_reconstruct = torch.randn_like(img_pool, dtype=torch.float) #标准正态分布
#构建反池化层(窗口、步长参数与池化层参数一一对应相等)
maxunpool_layer = nn.MaxUnpool2d((2, 2), stride=(2, 2))
#生成反池化后的图像
img_unpool = maxunpool_layer(img_reconstruct, indices)
print("raw_img:\n{}\nimg_pool:\n{}".format(img_tensor, img_pool))
print("img_reconstruct:\n{}\nimg_unpool:\n{}".format(img_reconstruct, img_unpool))
AdaptiveMaxPool2d和maxpooling层有什么区别呢?
Maxpool.
已知:input size, kernel, stride.
未知:Output size
AdaptiveMaxpool
已知 :input size, Output size
未知:kernel, stride
线性层(全连接层)
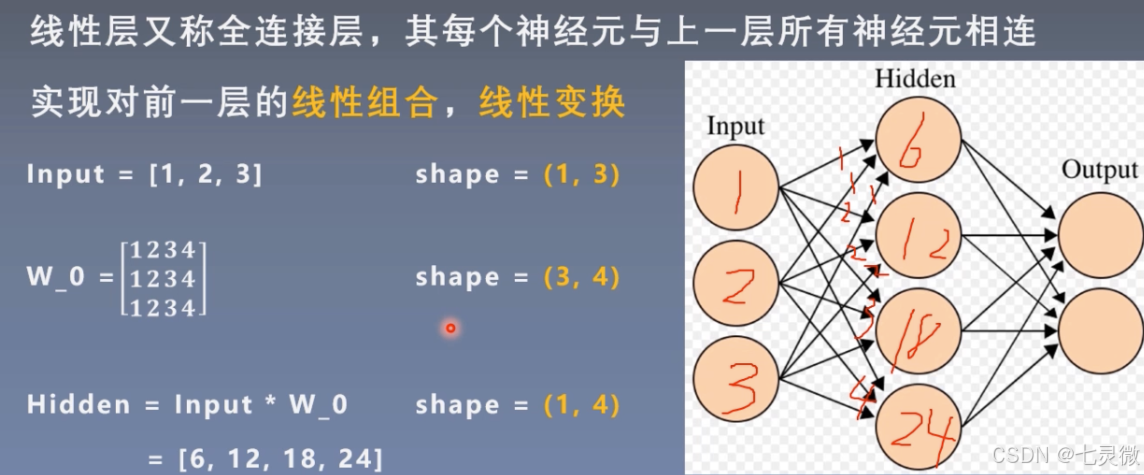
w_0第一行是input层第一个神经元传递给hidden层每个神经元的权值weight,同理…
如果有bias 还要加上bias。 y=wx+b
如果没有非线性激活函数,那么n层线性层==1层线性层
nn.Linear(in_features, out_features, bias=True, device=None, dtype=None)
'''
对一维信号(向量)进行线性组合;
参数:
in_features: 输入节点数;
in_features: 输出节点数;
bias: 是否需要偏置,默认为True;
'''
# ================ linear
flag = 1
if flag:
inputs = torch.tensor([[1., 2, 3]]) #1*3
linear_layer = nn.Linear(3, 4) #输入节点3个,输出节点4个
#w权值矩阵为4*3,每一行代表一个神经元与上一层神经元连接的权值。
linear_layer.weight.data = torch.tensor([[1., 1., 1.],
[2., 2., 2.],
[3., 3., 3.],
[4., 4., 4.]])
linear_layer.bias.data.fill_(0.5)
output = linear_layer(inputs)
print(inputs, inputs.shape)
print(linear_layer.weight.data, linear_layer.weight.data.shape)
#output=inputs*w^T+bias
print(output, output.shape) #输出的尺寸为1*4
激活函数层
- nn.Sigmoid
这个在逻辑回归里见过。

橙色曲线是其导数图像。
(1)多个网络层叠加后,导数范围会变得更小,甚至消失。
(2)输出不是0均值分布,破坏了数据分布。 - nn.Tanh

这个公式是怎么推导的?

导数<0时,网络非常深时,同样会梯度消失。 - nn.ReLu()修正线性单元

当多层网络不断使梯度叠加,会导致梯度爆炸;当累乘时可以缓解梯度消失。

nn.LeakyReLU(negative_slope=0.01, inplace=False)
LeakyReLU的slope参数0.01表示:负半轴0.01的斜率.

nn.PReLU(num_parameters=1, init=0.25, device=None, dtype=None)

num_parameters(整数):可学习参数 a 的数量,只有两种选择,要么定义成1,表示在所有通道上应用相同的 a进行激活,要么定义成输入数据的通道数,表示在所有通道上应用不同的 a进行激活,默认1。
init(float):a的初始值
输入数据的第二维度表示为通道维度,当输入维度小于2时,不存在通道维度,此时默认通道数为1
通过调用.weight方法来取出参数a
即使有多个 a,init也还是只能输入一个float类型的数
nn.RReLU(lower=0.125, upper=0.3333333333333333, inplace=False)
RReLU:斜率是随机的,符合均匀分布.
