【代码随想录训练营第42期 Day55打卡 - 图论Part5 - 并查集的应用
目录
一、并查集
适用范围
三大基本操作
二、经典题目
题目:卡码网 107. 寻找存在的路径
题目链接
题解:并查集
三、小结
一、并查集
适用范围
-
动态连通性问题:并查集可以判断两个节点是否在同一个连通分量中,这在处理网络连接、社交网络关系、图的连通性等场景中非常有用。
例如,在一个无向图中,可以快速判断两个顶点是否通过某些边相连。
-
图的简化:通过并查集,可以将一个图简化为若干个连通分量,每个连通分量可以看作一个超级节点,从而简化图的表示和分析。
-
网络延迟最小化:在网络中,通过并查集可以找到两点之间的最短路径,从而实现网络延迟的最小化。
-
等价类划分:并查集可以用于将元素划分为等价类,例如在编译原理中的符号表合并、类型检查等。
-
检测和处理成环问题:在某些问题中,需要检测是否存在环,并查集可以用于这类检测。
三大基本操作
1.初始化(Init):
初始化并查集,通常为每个元素创建一个单元素集合。
每个元素指向自己作为父节点,表示它是自己的集合的代表。
2.查找(Find):
查找元素所在的集合的代表(根节点)。
通常伴随着路径压缩优化,以加速后续的查找操作。
这里注意:路径压缩是指在查找一个节点的根节点时,将路径上的所有节点直接连接到根节点上。这样,下次查找这些节点时,可以直接到达根节点,而不需要再次遍历整个路径。
3.合并(Join或者Union):
将两个元素所在的集合合并为一个集合。
通常通过将一个集合的代表指向另一个集合的代表来实现。
并查集模板如下(几个基本操作):
void init() //初始化
{
for (int i = 1; i <= n; i++)
father[i] = i;
}
int find(int u) //查找
{
if (u != father[u])
father[u] = find(father[u]);
return father[u];
}
bool isSame(int u, int v) //判断两节点是否同一根节点(是否连通)
{
int rootu = find(u);
int rootv = find(v);
return rootu == rootv;
}
void join(int u, int v) //合并
{
int rootu = find(u);
int rootv = find(v);
if (rootu != rootv)
father[rootv] = rootu;
}
二、经典题目
题目:卡码网 107. 寻找存在的路径
题目链接
107. 寻找存在的路径 (kamacoder.com)
题目描述
给定一个包含 n 个节点的无向图中,节点编号从 1 到 n (含 1 和 n )。
你的任务是判断是否有一条从节点 source 出发到节点 destination 的路径存在。
输入描述
第一行包含两个正整数 N 和 M,N 代表节点的个数,M 代表边的个数。
后续 M 行,每行两个正整数 s 和 t,代表从节点 s 与节点 t 之间有一条边。
最后一行包含两个正整数,代表起始节点 source 和目标节点 destination。
输出描述
输出一个整数,代表是否存在从节点 source 到节点 destination 的路径。如果存在,输出 1;否则,输出 0。
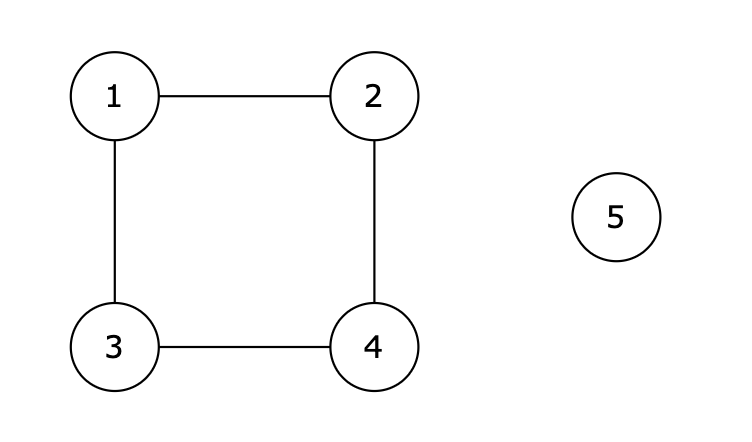
输入示例
5 4 1 2 1 3 2 4 3 4 1 4输出示例
1提示信息
数据范围:
1 <= M, N <= 100。
题解:并查集
这就是上边提到的适用范围的第一种:动态连通性问题 -- 判断两个顶点是否通过某些边相连。
其实就是模板的简单套用,最终只需要判断题目要求的节点 source 和节点 destination是否连通即可。
简述一下三大基本操作(含具体注释):
初始化:
// 并查集初始化
void init()
{
for (int i = 1; i <= n; i++) // 注意本题节点是从1到n
father[i] = i; // 初始化每个节点的父节点指向自己
}查找:
// 并查集里寻找该节点的根节点(带路径压缩)
int find(int u)
{
if (u != father[u]) // 如果当前节点不是根节点,就会递归地调用 find 函数来找到根节点,并将沿途的所有节点的父节点设置为根节点
father[u] = find(father[u]); // 路径压缩:将u的父节点设置为u的根节点
return father[u]; // 返回u的根节点
}合并:
// join 函数用于合并两个节点所在的集合:将v->u这条边加入并查集
void join(int u, int v)
{
int rootu = find(u); // u的根节点
int rootv = find(v); // v的根节点
if (rootu != rootv)
father[rootv] = rootu; // 将v-u这条边加入并查集:将节点 v 的根节点(也是 v 所在集合的代表)的父节点设置为 u 的根节点。这样,v 的根节点及其所有子节点(包括 v)现在都属于以 u 的根节点为代表的集合
}完整代码如下:
#include <bits/stdc++.h>
using namespace std;
int n; // 节点数量
vector<int> father = vector<int>(101, 0); // 并查集数据结构:节点编号从1到n,而题目节点个数最大为100 -- 故初始化大小101
// 并查集初始化
void init()
{
for (int i = 1; i <= n; i++) // 注意本题节点是从1到n
father[i] = i; // 初始化每个节点的父节点指向自己
}
// 并查集里寻找该节点的根节点(带路径压缩)
int find(int u)
{
if (u != father[u]) // 如果当前节点不是根节点,就会递归地调用 find 函数来找到根节点,并将沿途的所有节点的父节点设置为根节点
father[u] = find(father[u]); // 路径压缩:将u的父节点设置为u的根节点
return father[u]; // 返回u的根节点
}
// 判断u和v是否找到同一个根节点 -- 是否在同一个集合中
bool isSame(int u, int v)
{
int rootu = find(u);
int rootv = find(v);
return rootu == rootv;
}
// join 函数用于合并两个节点所在的集合:将v->u这条边加入并查集
void join(int u, int v)
{
int rootu = find(u); // u的根节点
int rootv = find(v); // v的根节点
if (rootu != rootv)
father[rootv] = rootu; // 将v-u这条边加入并查集:将节点 v 的根节点(也是 v 所在集合的代表)的父节点设置为 u 的根节点。这样,v 的根节点及其所有子节点(包括 v)现在都属于以 u 的根节点为代表的集合
}
int main()
{
int m, s, t, source, destination;
cin >> n >> m;
init(); // 初始化并查集
while (m--)
{
cin >> s >> t;
join(s, t); // 将s和t所在的集合合并(即将s-t这条边加入并查集)
}
cin >> source >> destination;
if (isSame(source, destination)) // 判断这两个节点是否在同一个集合中(是否连通)-- 有同一个根
cout << 1 << endl;
else
cout << 0 << endl;
}三、小结
并查集是一种常见的数据结构,在了解其基本操作的同时,更应该了解并查集是如何实现的,并且具有怎样的作用,这样才能加深对代码的理解。今天的打卡到此结束,后边会继续加油!