基于MATLAB/Simulink的模型降阶方法介绍

降阶建模ROM(Reduced order modeling) 和模型降阶MOR(Model order reduction) 是降低全阶高保真模型的计算复杂性，同时在令人满意的误差范围内保持预期保真度的技术。

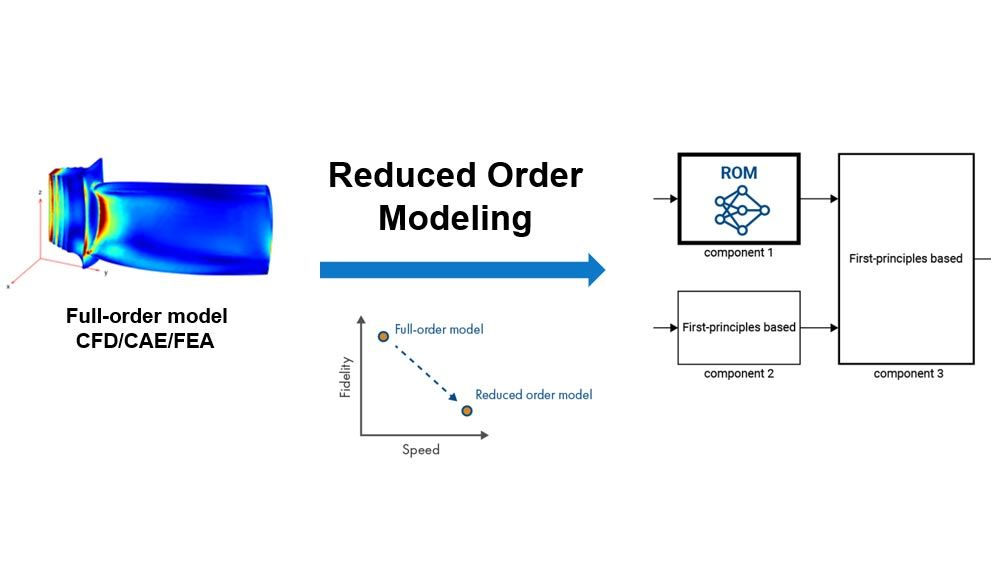
模型降阶技术可以解决科学计算邻域在建模仿真与工程应用中的几大痛点：

• 高保真模型计算量过高的问题（高精度CFD、CAE、FEA模型）
• 多尺度多物理场建模的问题（在气候模拟、航空航天）
• 反复求解迭代的问题（工程设计优化）
• 模型实时反馈的需求（系统的实时预测控制）

降阶建模或模型降阶技术的应用十分广泛，例如：

• 加速桌面系统仿真
• 硬件在环（HIL）测试
• 开发虚拟传感器
• 数字孪生
• 控制器的设计

模型降阶的方法

关于模型降阶方法的分类，没有一个完全统一或权威的定义，这主要是因为模型降阶是一个活跃的研究领域，新方法不断涌现，使得分类标准需要不断更新。

同时，模型降阶技术应用于多个学科，如工程学、物理学、计算机科学等，各学科可能有不同的分类方式。

此外，许多降阶方法结合了多种技术，难以严格划分到单一类别中。

对于MATLAB/Simulink而言，官方将构建降阶模型的方法分为以下几类：

1. 基于物理（Physics-Based)
2. 基于模型（Model-Based )
3. 线性化（Linearization）
4. 数据驱动的方法（Data-Driven ）

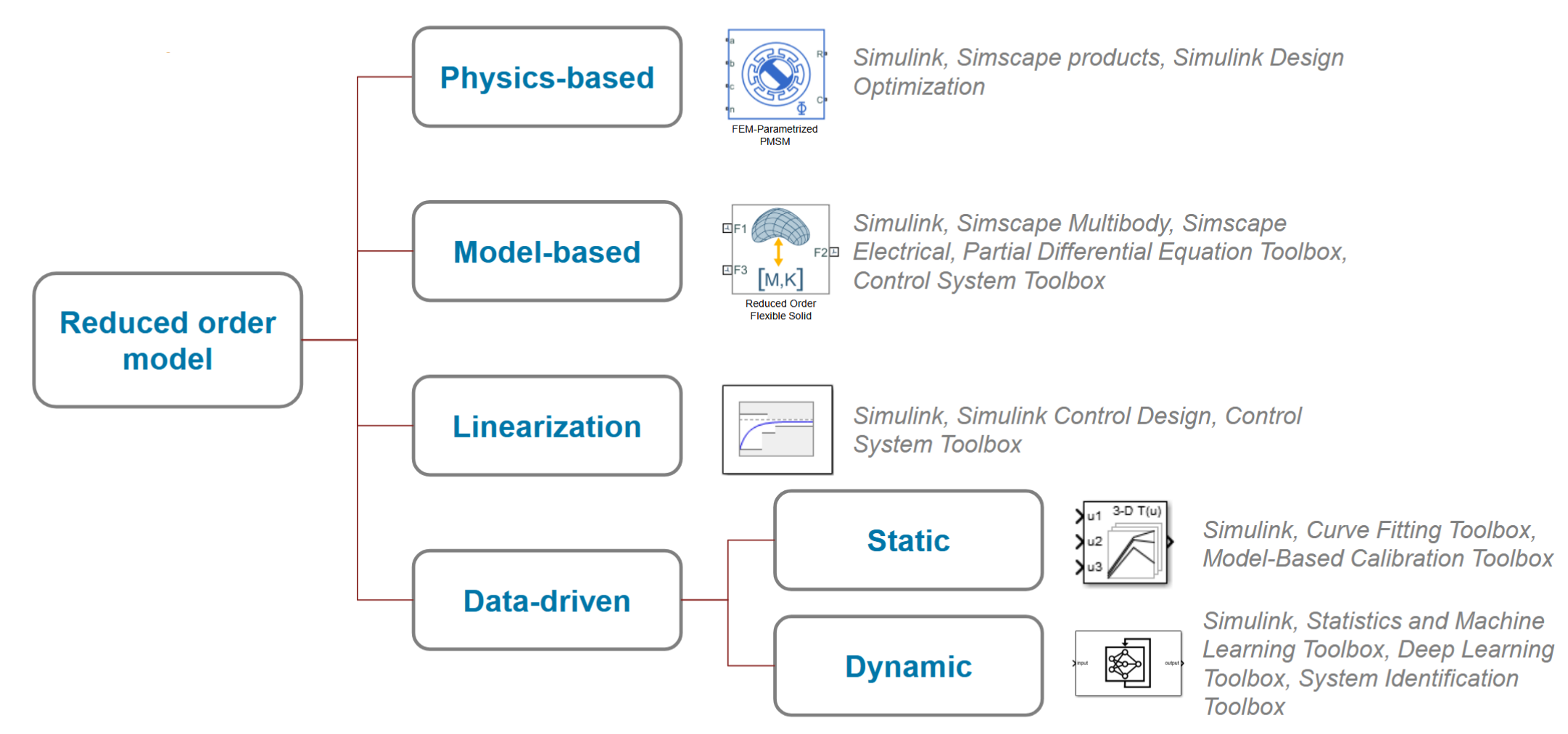
1. 基于物理的降阶

基于物理的降阶（Physics-Based Reduction）通过分析和简化物理模型来减少计算复杂性。

最常见的基于物理的降阶方法就是使用系统级的物理模型替代详细的元件级的物理模型，例如，将下图左侧的详细PMSM电机驱动模型，替换为PMSM电机驱动系统的降阶模型。

二者的差异在于：

• 系统级模型主要关注系统级特性（例如功率、扭矩、转速），适合初步系统设计和优化。

• 详细的（元件级）物理模型包含更多详细的电机参数（例如定子电阻、电感等）。

与之类似的，电池建模中的等效电路（Equivalent Circuit）模型也可看作是电化学(Single Particle)模型的基于物理的降阶。

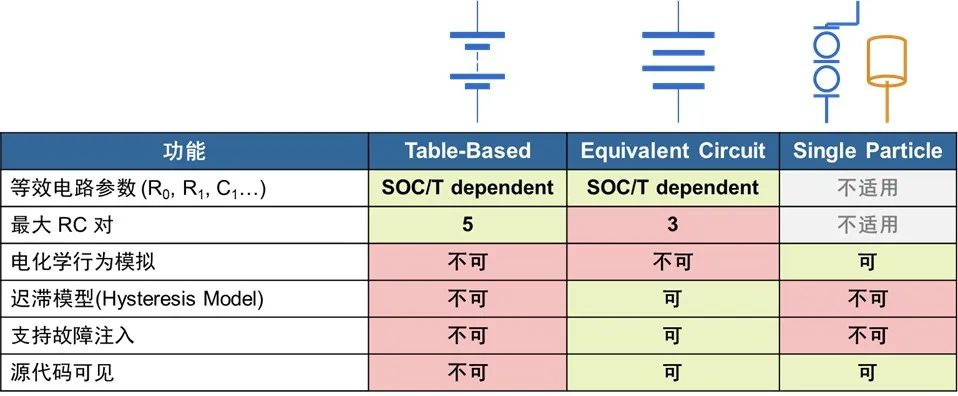
基于物理的降阶在流体、传热等邻域的应用也十分广泛。

2. 基于模型的降阶方法

基于模型（Model-Based )的降阶方法基于对系统的数学或物理建模。它利用已知的系统结构和动力学方程来创建一个简化但仍能捕捉系统主要特性的模型。

基于模型（Model-Based )的降阶方法一般有：

• Selection：消除目标频域范围外的特征。
• Approximation：找到并移除对目标输出影响小的特征。
• Simplification：通过取消零极点对或消除对整体模型响应没有影响的状态来精确降低模型阶数

基于模型的降阶方法能够保留系统的物理意义和结构，可以处理非线性系统，通常具有较好的外推性能。

其局限是需要对系统有深入的理解，而且可能难以处理高度复杂或未知结构的系统。

基于模型（Model-Based )的降阶方法与基于物理的方法（Physics-based）相比，两者都依赖于对系统的理论理解，但基于物理的方法更侧重于直接使用物理定律，而基于模型的方法可能包括更广泛的数学抽象。

3. 线性化

线性化（Linearization）是将非线性系统近似为线性系统的过程，通常是在某个工作点附近进行的小扰动假设下实现的，这是由于线性化通常通过泰勒级数展开来实现，保留一阶项而忽略高阶项，因此在工作点附近效果最佳，随着状态偏离工作点，模型精度会迅速下降。

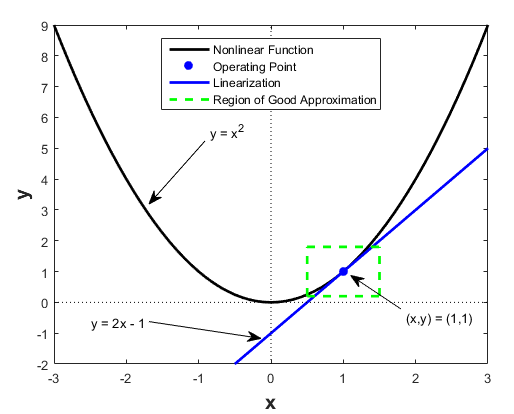
对于当工作点分布范围较大时，可以在多个工作点进行线性化，然后通过插值或切换来覆盖整个操作范围。

线性化在模型降阶中的主要应用是：

• 简化非线性系统：通过将复杂的非线性系统简化为线性系统，使得对系统的分析和控制设计变得更简单。
• 工作点分析：在特定的工作点处，线性化可以用来理解系统的局部动态特性。
• 用于控制器设计：线性化后的模型更易于使用线性控制理论进行设计，如PID控制、状态反馈等。

4. 数据驱动的降阶方法

在介绍数据驱动的模型降阶方法前，首先介绍一下两种不同的建模思路。

第一性原理建模（First-Principles Models） ：从基本的物理、化学、数学等科学原理出发构建模型。这种方法依赖于已知的理论、方程和领域知识，也就是所谓的白盒模型。

第一性原理建模的特点是：

• 有清晰的物理意义，可解释性强。
• 不需要数据工程
• 需要对应专业领域的知识
• 在某些情况下的复杂度过高难以建模。

数据驱动建模（Data-Driven Models） ：基于大量的历史数据或实时数据，利用统计学、机器学习、人工智能等技术直接从数据中学习系统规律和模式来进行建模，也就是黑盒模型。

数据驱动建模的特点是：

• 可解释性差。
• 可以充分利用现有的测试和仿真数据。
• 不需要太多专业领域的专知识。
• 需要大量的数据集。

第一性原理建模与数据驱动建模不是对立关系，二者可以同时存在，在实践中，很多有效的模型会同时结合这两种方法。

一般情况下，高保真的 FEA/CAE/CFD 模型都满足第一性原理建模的标准，这类模型可能需要数小时甚至数天的时间来模拟，因此难以适应硬件在环、控制器开发等场景。

数据驱动的模型降阶方法的核心思想就是使用原始高保真的第一性原理模型的输入输出数据来构建准确表示底层系统的降阶模型。

数据驱动的降阶模型可以是静态模型，也可以是动态模型。

静态模型用于没有时间依赖性的情况，仅需关注输入与输出的直接关系

动态模型则用于需要描述时间演化过程的系统，关注系统在时间上的动态响应。

4.1 基于数据驱动的静态模型降阶

基于数据驱动的静态（稳态）降阶方法包括：

4.1.1 曲线拟合

曲线拟合（Curve Fitting）是通过数学函数来近似描述一组数据点或复杂模型行为的方法。它试图找到一个相对简单的函数,能够最好地表示数据的整体趋势。

曲线拟合计算简单，易于实现，可以捕捉数据的主要趋势且结果易于理解和解释。但可能丢失重要的局部特征，在拟合范围之外的外推性能可能较差，选择合适的拟合函数形式需要经验和尝试。

曲线拟合在模型降阶中的应用包括：

• 简化复杂关系: 用简单的数学表达式替代复杂的模型关系。
• 参数减少: 大幅减少需要存储和计算的参数数量。
• 捕捉主要趋势: 保留数据或模型的主要特征,忽略次要细节。

曲线拟合的方法包括：

1. 多项式拟合
2. 指数拟合
3. 对数拟合
4. 幂律拟合
5. 非线性最小二乘法

4.1.2 查表

查表（Lookup Tables&Map图）的原理是预先计算并存储模型的输入-输出对应关系，将复杂的计算过程转化为简单的数据检索。

查表适用于输入范围有限的问题，可以极大提高运行时的计算速度，也可以处理难以用简单函数表达的复杂关系。但其可能需要大量内存存储表格数据，且精度受限于表格的分辨率，同时难以处理高维输入问题（维数灾难）。

在模型降阶中的应用包括：

• 计算简化: 将复杂的计算过程替换为快速的内存访问。
• 离散化: 对连续函数进行离散化,减少运行时计算。
• 实时性能提升: 特别适用于对计算速度要求高的实时系统。

4.1.3 主成分分析

主成分分析(PCA)是一种统计方法，通过正交变换将一组可能相关的变量转换为一组线性不相关的变量（主成分）。这些主成分按方差大小排序，保留最大方差的几个主成分可以大幅降低数据维度。

主成分分析可以显著降低数据维度，去除数据中的噪声和冗余，同时保留数据中的主要变化信息。但其建立在数据是线性可分的假设上，可能会丢失一些对任务重要但方差小的特征，对于在高维数据结果难以解释。

主成分分析在模型降阶中的应用包括：

• 降维: 大幅减少特征空间的维度。
• 特征选择: 识别并保留数据中最重要的特征。
• 去噪: 通过去除小方差的主成分,可以去除数据中的噪声。

4.1.4 特征提取

特征提取（Feature Extraction）是从原始数据中选择或构造最相关、最有信息量的特征的过程。它旨在减少数据的冗余,同时保留对特定任务最有用的信息。

特征提取可以大幅减少数据维度，提高模型的解释性和泛化能力，结合相关专业领域的知识，可以提取更有意义的特征。

但手动特征工程耗时且主观，自动特征提取方法（如深度学习）可能需要大量数据和计算资源。

特征提取在模型降阶中的应用：

• 维度降低: 从高维数据中提取关键信息,减少特征数量。
• 模型简化: 通过减少输入特征,简化模型结构。
• 性能提升: 通过选择最相关的特征,提高模型的性能和泛化能力。

特征提取的方法包括：

1. 基于过滤（Filter）的方法（如方差阈值、相关系数）
2. 基于包装（Wrapper）的方法（如递归特征消除）
3. 基于嵌入（Embedded）的方法（如L1正则化）
4. 自动编码器
5. 领域特定的特征工程

4.1.5 基于统计的机器学习方法

基于统计的机器学习模型可以用于模型降阶，其利用统计学原理来构建和训练模型以进行数据分析和预测。这类模型通过分析数据的概率分布和关系，来识别模式、提取特征并进行决策。

基于统计的机器学习模型包括：线性回归（Linear Regression）、逻辑回归（Logistic Regression）、朴素贝叶斯（Naive Bayes）、支持向量机（Support Vector Machine, SVM）、决策树（Decision Tree）、随机森林（Random Forest）等

4.2 基于数据驱动的动态模型降阶

可以使用以下技术开发动态 ROM：

4.2.1 非线性 ARX 模型

非线性 ARX 模型（Nonlinear ARX Models）通过使用非线性函数（如神经网络、核方法等）对输入和输出之间的关系进行建模，是一种用于动态系统的非线性建模方法。它们在模型降阶中的应用主要包括：

• 简化复杂系统的动态建模，通过捕捉系统的输入-输出关系。
• 提供一种数据驱动的方式来替代复杂的高维物理模型，适合实时性要求高的应用。
• 适合在系统辨识和控制应用中进行降阶处理，尤其是在不完全了解系统内部状态的情况下。

非线性ARX模型由模型回归量和输出函数组成，通过两阶段过程来预测未来值：

1. 模型将输入/输出信号转换为有限维度的回归量，这些回归量是基于信号的时间延迟值生成的特征。
2. 输出函数通过一个或多个映射对象将这些回归量映射到预测输出。每个映射对象可包含一个线性函数和一个非线性函数,它们作用于回归量以生成模型输出，并包含一个该输出的固定偏移量。

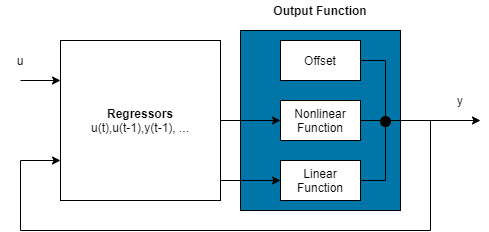
这种结构使得非线性ARX模型能够捕捉复杂的动态系统行为。

4.2.2 神经状态空间模型

神经状态空间模型（Neural State-Space Models）是一种非线性状态空间模型，其中状态转移和测量函数使用神经网络进行建模。

状态空间模型是使用状态方程和输出方程来表示动态系统的一种方式，状态方程是一组一阶常微分方程（ODEs）或差分方程，通常由第一性原理（白箱建模）推导而来。然而在实际应用中，由于缺乏先验知识或系统固有的复杂非线性动态特性，找到能准确描述系统的解析方程往往并非易事。

在这些情况下，通过神经网络表示非线性系统的状态方程和输出方程是一种有效的替代方案。

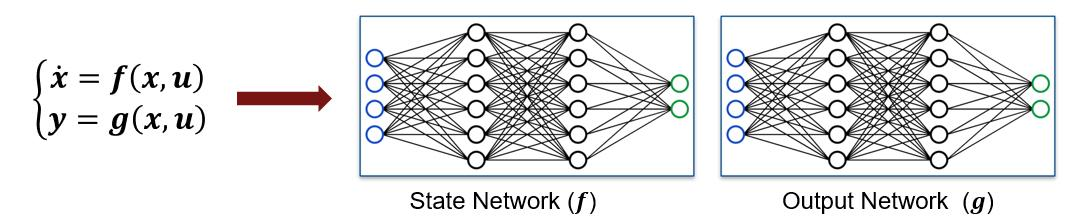
例如，对于连续时间非线性系统，可以使用多层感知器（MLP）网络来近似状态方程。网络的输入是 x 和 u，即系统状态向量和输入向量，网络的输出是 ẋ，即系统状态导数向量。

类似地，当存在非平凡的输出方程（即 y ≠ x）时，可以使用另一个 MLP 网络来近似它。对于这个网络，输入同样是 x 和 u，而网络输出是 y，即测量的系统输出。

4.2.3 长短期记忆网络（LSTM）

LSTM是一种特殊的循环神经网络(RNN)结构，在处理序列数据和时间序列预测方面表现出色。

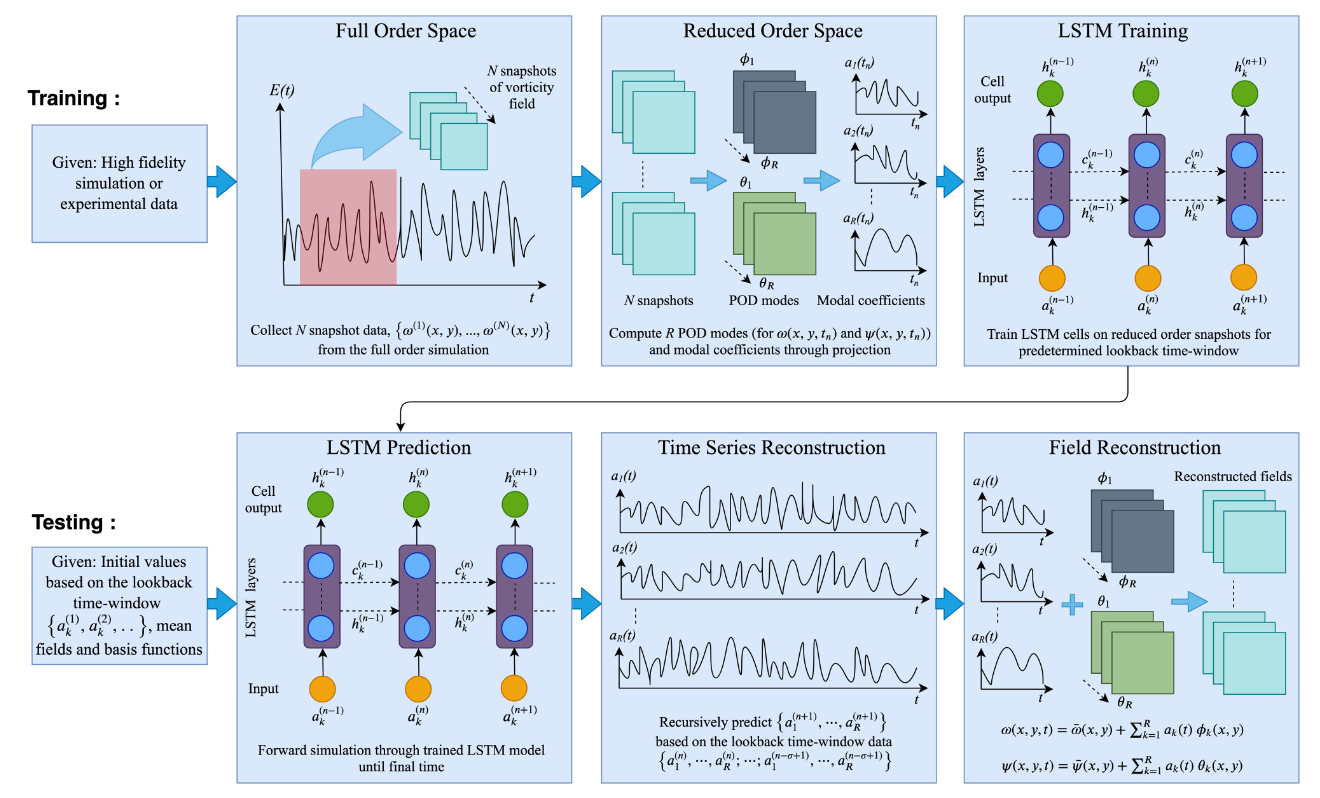
在模型降阶领域,LSTM主要有以下几个应用:

• 非线性动力系统降阶：LSTM通过学习非线性动力系统的低维表示，可以有效地重构和预测高维状态。这种方法特别适用于复杂的非线性系统，因为它能够捕捉到系统中隐含的非线性特征。
• 时间序列数据压缩：LSTM在处理高维时间序列数据时，能够提取重要的特征，这样就实现了数据的降维和压缩。这对于大数据分析和特征提取具有很大的实用价值。
• 参数化降阶模型：LSTM可以作为非线性映射工具，将高维系统状态映射到低维潜在空间，形成一个参数化的降阶模型。这种方法使得降阶模型可以更加灵活和准确地描述原始系统的动态。
• 与传统降阶方法结合：LSTM与传统的降阶方法（如POD）结合，可以弥补传统方法在非线性处理能力上的不足，提升降阶模型的精度和泛化能力。这种结合能够实现对复杂系统的更有效降阶。
• 自编码器结构：基于LSTM的自编码器结构能够学习数据的非线性低维表示，保留时间序列的时间相关性。这种方法特别适用于需要同时考虑时间依赖和降维的应用场景。

LSTM在模型降阶领域的应用充分利用了其处理序列数据和捕捉长期依赖的能力，同时保持了系统的动态特性

4.2.4 前馈神经网络

前馈神经网络（Feedforward Neural Networks）是一种人工神经网络,其中信息只向前传播,不存在循环或反馈。典型的FNN包含以下层:

• 输入层: 接收原始数据
• 隐藏层: 一个或多个,进行数据处理
• 输出层: 产生最终结果

每层由多个神经元(节点)组成，相邻层之间的神经元通过权重连接。

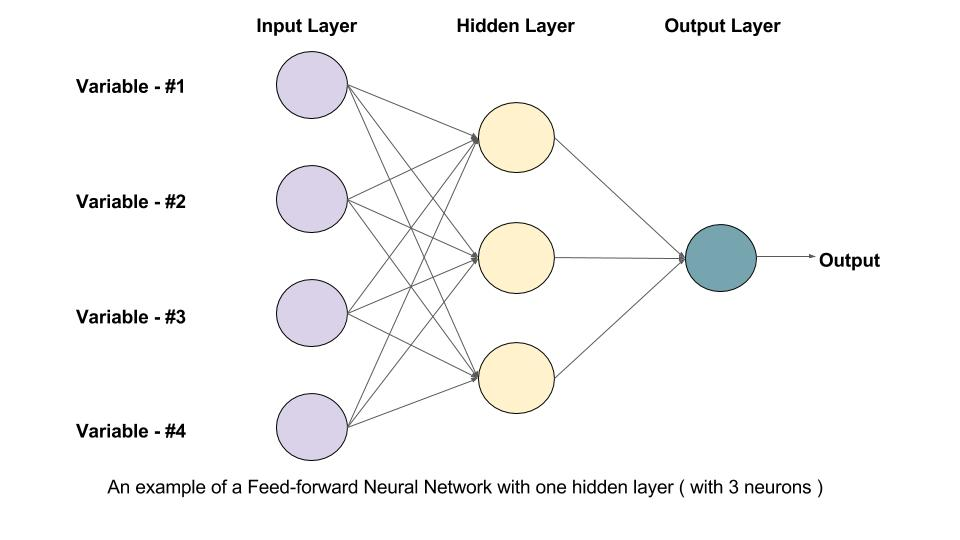
其工作原理为：

1. 前向传播: 数据从输入层开始，经过隐藏层,最后到达输出层。每个神经元接收上一层的输入，进行加权和，然后通过激活函数产生输出。
2. 激活函数: 常用的有ReLU，sigmoid，tanh等,引入非线性，使网络能够学习复杂的非线性关系。
3. 反向传播: 训练过程中，网络通过比较输出与目标值的差异(损失函数)，反向调整权重，最小化误差。
4. 优化算法: 如随机梯度下降(SGD)，用于更新权重，使网络逐步学习到输入和输出之间的映射关系。

FNN可用于模型降阶的原因：

• 非线性映射能力: FNN能够学习和表示复杂的非线性关系,这对于捕捉高维系统的非线性动态至关重要。
• 自动特征提取: 多层结构使FNN能够自动从原始高维数据中提取关键特征,无需手动设计特征提取器。
• 灵活性: FNN的结构(层数、每层神经元数)可以根据具体问题调整,适应不同复杂度的降阶任务。
• 端到端学习: FNN可以直接学习从高维输入到低维表示的映射,无需中间步骤。

此外，结合物理驱动的模型和数据驱动的 FNN，可以开发混合降阶方法。这种方法保留了物理模型的可靠性，同时利用 FNN 的灵活性和强大的非线性拟合能力，进一步提升模型的精度和计算效率。

4.2.5 神经常微分方程

神经常微分方程（Neural ODEs）是将神经网络与常微分方程(ODEs)相结合的一种深度学习模型，允许连续时间建模，并可以看作是具有无限多层的残差网络的极限。

神经常微分方程可以用于降低复杂动力系统模型的阶数，同时保持系统的关键动态特性，适合处理高维复杂系统。

它们的降阶应用包括：

• 提供连续时间系统的紧凑表示，可以高效地进行动态系统的降阶。
• 适合处理高维、复杂动态系统，能够在保持模型准确性的同时显著降低模型的复杂度。
• 在需要精确描述系统动态行为的场景中（如物理仿真、控制系统等）特别有用。

总结

此外还有类似POD、Krylov subspace、CGM、GMRES、PRIMA、SPRIM 等降阶方法。

这些方法大多用于不同领域的数值仿真、优化和模型简化，包括机械、电子、电磁等工程问题。

在MATLAB/Simulink中不但可以借助内置的各类工具箱实现模型降阶，也可以通过MORLAB这类第三方工具箱实现。

对于基于物理与模型的降阶而言，MATLAB对第三方CAE/CFD/FAE软件的兼容性在不断地提高，同时也支持最新的FMI/FMU模型的导入。

对于数据驱动的模型降阶，近年来新版本的MATLAB对PyTorch、TensorFlow、ONNX等框架的支持愈加完善，支持将最新的深度学习算法应用于模型降阶。