当前位置： 首页 > article >正文

数据结构不再难懂：带你轻松搞定图

article 2024/11/13 16:54:48

数据结构入门学习（全是干货）——图

1 图

1.1 什么是图

图是一种用于表示多对多关系的数学模型。它由一组顶点和一组边构成，用于描述事物之间的复杂关联。

  • 顶点：通常用 V (Vertex) 表示，代表事物或对象。
  • 边：通常用 E (Edge) 表示，代表顶点之间的连接。边可以是无向的（双向）或有向的（单向）。
    • 无向边：(v, w)，表示顶点 v 和 w 之间相互连接，没有方向性。
    • 有向边：<v, w>，表示从 v 到 w 有方向的连接。
图的抽象数据类型 (ADT)

  • 类型名称：图 (Graph)

  • 数据对象：G(V, E) 表示图由顶点集合 V 和边集合 E 构成。顶点集合不能为空，但边可以为空。

  • 操作：

    • 添加顶点和边。
    • 遍历图的所有顶点和边。
    • 查询图的属性，如顶点的度数、两顶点之间是否存在边等。
    
1. Graph Create()：建立并返回空图
2. Graph InsertVertex(Graph G, Vertex v)：将v插入G
3. Graph InsertEdge(Graph G, Edge e)：将e插入G;
4. void DFS(Graph G,Vertex v)：从顶点v出发深度优先遍历图G;
5. void BFS(Graph G,Vertex v)：从顶点v出发宽度优先遍历图G;
6. void ShortestPath(Graph G,Vertex v,int Dist[])：计算图G中顶点v到任意其他顶点的最短距离
7. void MST(Graph G)：计算图G的最小生成树
常见术语
  1. 无向图：没有方向的边连接顶点。
  2. 有向图：每条边都有方向，如箭头从一个顶点指向另一个顶点。
  3. 权重：边上标记的数字，通常表示该连接的成本、距离或权值。
  4. 网络：带权重的图称为网络。

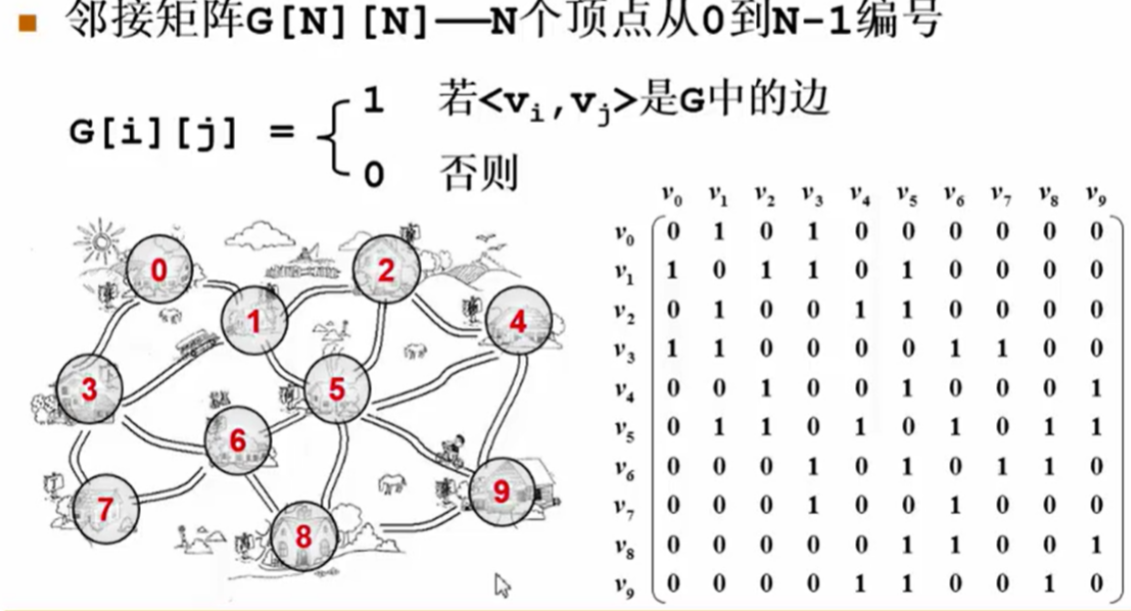
1.2 图的表示法——邻接矩阵

邻接矩阵是一种常用的表示图的方法，使用二维数组表示顶点之间的连接关系。

  • 无向图：邻接矩阵是对称的。matrix[i][j] 表示顶点 i 和顶点 j 之间是否有边。
  • 有向图：矩阵的行和列代表了方向关系，matrix[i][j] 表示从顶点 i 到顶点 j 是否有边。

怎么在程序中表示一个图

邻接矩阵的优缺点

  • 优点：

    • 直观、简单，易于理解和实现。
    • 检查任意两个顶点间是否有边十分方便。
    • 快速找到某一顶点的邻接点和计算顶点的度（有向图中分为出度和入度）。

  • 缺点：

    • 对于稀疏图（顶点多而边少），邻接矩阵会浪费大量存储空间。
    • 对稀疏图，统计边的数量会比较耗时。

1.3 图的表示法——邻接表

邻接表是另一种表示图的方法，适用于稀疏图。

  • 每个顶点对应一个链表，链表中的节点存储的是该顶点的所有邻接点。
  • 无向图：每条边 (v, w) 会在 v 和 w 的链表中各自存储一次。
  • 有向图：每条有向边 <v, w> 只会在 v 的链表中存储。

邻接表的优缺点

  • 优点：

    • 更适合存储稀疏图，节省空间。
    • 找出一个顶点的所有邻接点非常高效。
    • 适合计算顶点的度。

  • 缺点：

    • 检查任意两个顶点是否相邻需要遍历链表，效率不如邻接矩阵。
    • 不能快速统计边的数量。

2 图的遍历

图的遍历就是访问图中每个顶点一次，遍历过程中要确保每个顶点只访问一次。图的遍历通常有两种主要方法：深度优先搜索 (DFS) 和广度优先搜索 (BFS)。

2.1 图的遍历——深度优先搜索 (DFS)

深度优先搜索是一种递归的遍历方法，沿着图中的一条路径一直走到底，再回溯到上一层节点，继续沿另一条路径遍历，直至遍历所有顶点。

DFS 算法步骤：
  1. 从某个顶点开始，标记为已访问。
  2. 递归访问该顶点的未访问邻接点，直到所有邻接点都被访问。
  3. 回溯到上一个顶点，重复上述过程，直到遍历完所有顶点。

DFS 的实现可以用递归或显示栈来管理回溯过程。

void DFS(Vertex V)//从迷宫的节点出来
{
    visited[V] = true;//给每个节点一个变量，true相当于灯亮了，false则是熄灭状态
    for(V的每个邻接点W)//视野看得到的灯
        if(!visited[W])//检测是否还有没点亮的
            DFS(W);//递归调用
}

//类似树的先序遍历
若有N个顶点、E条边，时间复杂度是
    用邻接表存储图，有O(N+E)//对每个点访问了一次，每条边也访问了一次
    用邻接矩阵存储图，有O(N²)//V对应的每个邻接点W都要访问一遍
DFS 的时间复杂度：
  • 对于使用邻接表存储的图，时间复杂度为 O(V + E)，其中 V 是顶点数，E 是边数。
  • 对于使用邻接矩阵存储的图，时间复杂度为 O(V^2)。

2.2 图的遍历——广度优先搜索 (BFS)

广度优先搜索是一种层次遍历方法，从某个顶点出发，依次访问所有距离该顶点为一层的节点，然后再访问下一层节点，直到所有节点都被访问。

BFS 算法步骤：

void BFS(Vertex V)
{
    visited[V] = true;
    Enqueue(V,Q);//压到队列里
    while(!IsEmpty(Q)){
        V = Dequeue(Q);//每次循环弹出一个节点
        for(V的每个邻接点W)
            if(!visited[W]){//没有访问过的去访问将其压入队列中
                visited[W] = true;
                Enqueue(W,Q);
            }
    }
}
  1. 从某个顶点开始，标记为已访问并将其加入队列。
  2. 从队列中取出顶点，访问它的所有未访问的邻接点，并将这些邻接点加入队列。
  3. 重复上述过程，直到队列为空，表示所有顶点都已访问。
BFS 的时间复杂度：
  • 对于使用邻接表存储的图，时间复杂度为 O(V + E)。
  • 对于使用邻接矩阵存储的图，时间复杂度为 O(V^2)。

2.3 为什么需要两种遍历方法？

  • DFS：适用于需要尽可能深入遍历的情况，特别是当需要探索路径时，比如解决迷宫问题。
  • BFS：适用于需要层次遍历的情况，如寻找最短路径等。

2.4 图不连通怎么办？

在遍历图时，如果图不连通，意味着某些顶点无法通过一条路径到达其他顶点。此时，需要对每个连通分量分别进行遍历。

连通的相关概念：
  • 连通图：在无向图中，任意两个顶点之间都有路径。
  • 连通分量：无向图中的极大连通子图。
  • 回路：从一个顶点出发，经过若干条边回到起始顶点的路径。

在遍历非连通图时，可以使用 DFS 或 BFS 多次遍历，每次从未访问的顶点开始，直到遍历完所有连通分量。

3 应用实例：拯救 007

在这个应用实例中，可以通过图的遍历（DFS 或 BFS）来模拟 007 从一个顶点逃脱到另一个顶点的场景。目标是从起始顶点开始，找到一条通往安全点的路径。


void Save007(Graph G)
{
    for(each V in G){
        if(!visited[V] && FirstJump(V)){//这个FirstJump(V)是007第一跳有没有可能从孤岛跳到V上有没有可能，有且没踩过就跳上去
            answer = DFS(V);//or BFS(V)
            if(answer == YES) break;0
        }
    }
    if(answer == YES) output("Yes");
    else output("No");
}
DFS 解决方案：
  1. 以起点作为图中的一个顶点。
  2. 使用 DFS 递归地查找逃脱路径。
  3. 如果找到了逃脱路径，输出路径；如果没有找到，则输出“没有路径”。

void DFS(Vertex V)
{
    visited[V] = true;//表示鳄鱼头踩过了
    if(IOsSafe(V)) answer = YES;
    else{
    for(each W in G )
        if(!visited[W] && Jump(V,W)){//可以从V jump跳到这个w上面，作用是算V到W之间的距离是不是小于007可以跳跃最大距离
          answer = DFS(W);//递归 
            if(answer == YES) break;
        }
    }
        return answer;
}
BFS 解决方案：
  1. 从起点开始，使用队列存储每个可能的逃脱路径。
  2. 广度优先地寻找最短逃脱路径。
  3. 输出找到的路径，如果没有找到，输出“没有路径”。

4 应用实例：六度空间理论

六度空间理论 (Six Degrees of Separation) 表示在一个社交网络中，任意两个人之间通过不超过六个人的中间连接，就可以建立联系。

社交网络图：
  1. 将社交网络建模为一个无向图，顶点表示人，边表示两个人之间的社交联系。
  2. 通过图的遍历（如 BFS）计算每个人到其他人的最短路径，验证六度空间理论的正确性。
  3. 计算符合六度空间理论的顶点数量占总顶点数量的百分比。
算法思路
1.对每个节点进行广度优先搜索
2.搜索过程中累计访问的节点数
3.需要记录"层"数,仅计算6层以内的节点数
    
void SDS()
{
    for(each V in G){
        count += BFS(V);
        Output = (count/N);
    }
}

//结合最初的BFS
    void BFS(Vertex V)
{
    visited[V] = true;count = 1;
    Enqueue(V,Q);//压到队列里
    while(!IsEmpty(Q)){
        V = Dequeue(Q);//每次循环弹出一个节点
        for(V的每个邻接点W)
            if(!visited[W]){//没有访问过的去访问将其压入队列中
                visited[W] = true;
                Enqueue(W,Q);count++;
            }
    }return count;
}

5 小白专场：如何用 C 语言建立图

在 C 语言中，图的实现通常使用邻接矩阵或邻接表来存储顶点和边的关系。

5.1 邻接矩阵实现

邻接矩阵的结构：
typedef struct {
    int VertexNum;
    int EdgeNum;
    int Matrix[MAXV][MAXV]; // 邻接矩阵
} MGraph;
初始化图：
MGraph* CreateGraph(int VertexNum) {
    MGraph *Graph = (MGraph *)malloc(sizeof(MGraph));
    Graph->VertexNum = VertexNum;
    Graph->EdgeNum = 0;
    
    for (int i = 0; i < VertexNum; i++) {
        for (int j = 0; j < VertexNum; j++) {
            Graph->Matrix[i][j] = 0; // 初始化无边的图
        }
    }
    
    return Graph;
}
插入边：
void InsertEdge(MGraph *Graph, int v1, int v2, int weight) {
    Graph->Matrix[v1][v2] = weight; // 插入边 v1 -> v2
    Graph->EdgeNum++;
}

5.2 邻接表实现

邻接表的结构：
typedef struct AdjVNode {
    int AdjV;
    struct AdjVNode *Next;
} AdjVNode;

typedef struct VNode {
    AdjVNode *FirstEdge;
} VNode, AdjList[MAXV];

typedef struct {
    AdjList G;
    int VertexNum;
    int EdgeNum;
} LGraph;
初始化邻接表：
LGraph* CreateGraph(int VertexNum) {
    LGraph *Graph = (LGraph *)malloc(sizeof(LGraph));
    Graph->VertexNum = VertexNum;
    Graph->EdgeNum = 0;
    
    for (int i = 0; i < VertexNum; i++) {
        Graph->G[i].FirstEdge = NULL;
    }
    
    return Graph;
}
插入边：
void InsertEdge(LGraph *Graph, int v1, int v2) {
    AdjVNode *NewNode = (AdjVNode *)malloc(sizeof(AdjVNode));
    NewNode->AdjV = v2;
    NewNode->Next = Graph->G[v1].FirstEdge;
    Graph->G[v1].FirstEdge = NewNode;
    Graph->EdgeNum++;
}

通过邻接矩阵和邻接表两种方式，可以高效地存储和操作图结构，并进一步应用到图的遍历和各种图算法的实现中。


http://www.kler.cn/a/313337.html

相关文章：

  • C++组合复用中，委托的含义与作用
  • 洞察鸿蒙生态，把握开发新机遇
  • 7天用Go从零实现分布式缓存GeeCache（学习）（3）
  • 【Python TensorFlow】进阶指南（续篇一）
  • 【Elasticsearch入门到落地】1、初识Elasticsearch
  • Redis主从复制（replication）
  • linux-L6 linux管理服务的启动、重启、停止、重载、查看状态命令
  • EmguCV学习笔记 VB.Net 12.3 OCR
  • OpenAI GPT o1技术报告阅读（4）- 填字游戏推理
  • 【Git 操作】Git 的基本操作
  • Elasticsearch：检索增强生成背后的重要思想
  • 【VUE3.0】动手做一套像素风的前端UI组件库---先导篇
  • 社团周报系统可行性研究-web后端框架对比-springboot，django，gin
  • Linux内核学习之 -- ARMv8中的Current宏
  • 自注意力与多头自注意力的区别
  • Go进阶概览 -【7.2 泛型的使用与实现分析】
  • 网络穿透：TCP 打洞、UDP 打洞与 UPnP
  • SAP HCM 组织增量解决方案
  • FSFP——专为蛋白质工程设计的少样本学习策略
  • SpringMVC1~~~
  • 回归预测 | Matlab实现SSA-HKELM麻雀算法优化混合核极限学习机多变量回归预测
  • 动手学深度学习（五）循环神经网络RNN
  • 吃透这本大语言模型入门指南，LLM就拿下了
  • 【Kubernetes】常见面试题汇总（二十八）
  • RedisTemplate操作ZSet的API
  • 《让手机秒变超级电脑！ToDesk云电脑、易腾云、青椒云移动端评测》