神经网络修剪实战
修剪神经网络是一个古老的想法,可以追溯到 1990 年(Yan Lecun 的最佳脑损伤工作)甚至更早。这个想法是,在网络中的众多参数中,有些是多余的,对输出的贡献不大。
如果你可以根据网络中神经元的贡献程度对它们进行排序,那么你就可以从网络中删除排名较低的神经元,从而得到一个更小、更快的网络。

NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - AI模型在线查看 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割
获得更快/更小的网络对于在移动设备上运行这些深度学习网络非常重要。
可以根据神经元权重的 L1/L2 平均值、它们的平均激活、神经元在某些验证集上不为零的次数和其他创造性方法进行排名。修剪后,准确度会下降(如果排名巧妙,希望不会下降太多),并且网络通常会经过更多训练以恢复。
如果我们一次修剪太多,网络可能会受到严重损坏,无法恢复。
因此,在实践中,这是一个迭代过程 - 通常称为“迭代修剪”:修剪/训练/重复。
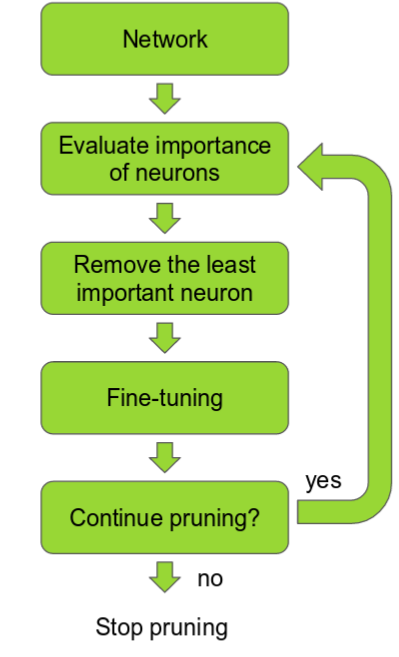
图片取自 [1611.06440 修剪卷积神经网络以实现资源高效推理]
1、听起来不错,为什么它不那么流行呢?
有很多关于修剪的论文,但我从未在现实生活中的深度学习项目中遇到过修剪。
考虑到在移动设备上运行深度学习的所有努力,这令人惊讶。我猜原因是以下几点:
- 到目前为止,排名方法还不够好,导致准确率下降太大。
- 实施起来很麻烦。
- 那些使用修剪的人,把它当作自己的秘密优势。
所以,我决定自己实施修剪,看看我是否能用它得到好的结果。
在这篇文章中,我们将介绍几种修剪方法,然后深入研究其中一种方法的实施细节。
我们将微调 VGG 网络以在 Kaggle Dogs vs Cats 数据集上对猫/狗进行分类,这代表了一种我认为在实践中非常常见的迁移学习。
然后我们将修剪网络,使其速度提高近 3 倍,并将大小缩小近 4 倍!
2、修剪目标:速度 vs. 尺寸
在 VGG16 中,90% 的权重位于完全连接的层中,但这些层仅占总浮点运算的 1%。
直到最近,大多数工作都集中在修剪完全连接的层上。通过修剪这些层,可以大大减小模型大小。
我们将重点介绍如何修剪卷积层中的整个过滤器。
但这也有减少内存的酷副作用。正如 [1611.06440 修剪卷积神经网络以实现资源高效推理] 论文中所观察到的,层越深,修剪的就越多。
这意味着最后一个卷积层将被大量修剪,并且其后的完全连接层中的许多神经元也将被丢弃!
在修剪卷积滤波器时,另一种选择是减少每个滤波器中的权重,或删除单个内核的特定维度。最终可能会得到稀疏的滤波器,但计算速度的提高并非易事。最近的研究提倡“结构化稀疏性”,即修剪整个滤波器。
这些论文中有几个表明了一件重要的事情,即通过训练然后修剪更大的网络,特别是在迁移学习的情况下,他们得到的结果比从头开始训练较小的网络要好得多。
现在让我们简要回顾一下几种方法。
- [1608.08710 修剪滤波器以实现高效的卷积网络]
在这项工作中,他们提倡修剪整个卷积滤波器。 修剪索引为 k 的滤波器会影响它所在的层和下一层。 下一层索引 k 处的所有输入通道都必须删除,因为修剪后它们将不再存在。
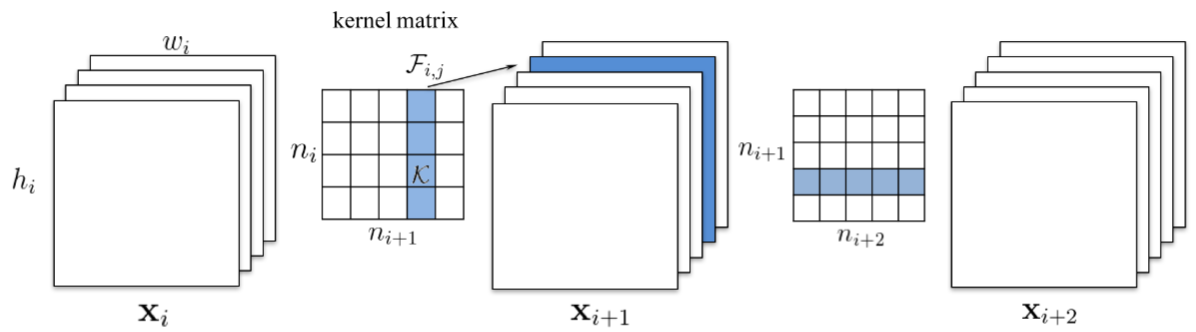
图片来自 [1608.08710 修剪过滤器以实现高效卷积网络]
如果下一层是全连接层,并且该通道的特征图大小为 MxN,则从全连接层中删除 MxN 个神经元。
这项工作中的神经元排名相当简单。它是每个过滤器权重的 L1 范数。
在每次修剪迭代中,他们对所有过滤器进行排名,在所有层中全局修剪排名最低的 m 个过滤器,重新训练并重复。
- [1512.08571 深度卷积神经网络的结构化修剪]
这项工作看起来很相似,但排名要复杂得多。他们保留一组 N 个粒子过滤器,它们代表要修剪的 N 个卷积过滤器。
当粒子所代表的过滤器未被屏蔽时,根据验证集上的网络准确度为每个粒子分配一个分数。然后根据新的分数对新的修剪掩码进行采样。
由于运行此过程很繁重,他们使用了一个小型验证集来测量粒子分数。
- [1611.06440 修剪卷积神经网络以实现资源高效推理]
这是 Nvidia 的一项非常酷的工作。
首先,他们将修剪问题表述为组合优化问题:选择权重 B 的子集,这样在修剪它们时网络成本变化将最小。

请注意他们如何使用绝对差异而不仅仅是差异。使用绝对差异可以确保修剪后的网络不会过多地降低网络性能,但也不应该增加网络性能。他们在论文中表明这会产生更好的结果,大概是因为它更稳定。
现在,所有排名方法都可以通过这个成本函数来判断。
- Oracle 修剪
VGG16 有 4224 个卷积滤波器。“理想”的排名方法将是强力的 - 修剪每个滤波器,然后观察在训练集上运行时成本函数如何变化。由于他们来自 Nvidia,并且可以使用数以亿计的 GPU,所以他们就是这么做的。这称为 oracle 排名 - 最小化网络成本变化的最佳排名。现在,为了衡量其他排名方法的有效性,他们计算了与 oracle 的 Spearman 相关性。令人惊讶的是,他们提出的排名方法(下文介绍)与 oracle 的相关性最高。
他们提出了一种新的神经元排名方法,该方法基于网络成本函数的一阶(意味着计算速度快)泰勒展开。
修剪滤波器 h 与将其归零相同。
当网络权重设置为 W 时,C(W, D) 是数据集 D 上的平均网络成本函数。现在我们可以将 C(W, D) 评估为 C(W, D, h = 0) 周围的扩展。它们应该非常接近,因为删除单个过滤器不会对成本产生太大影响。
h 的排名为 abs(C(W, D, h = 0) - C(W, D))。
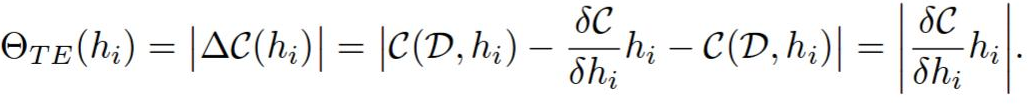
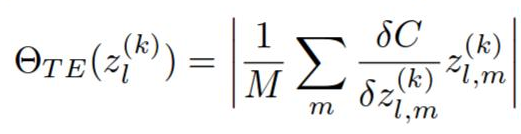
然后通过该层中排名的 L2 范数对每一层的排名进行归一化。我猜这是一种经验主义,我不确定为什么需要这样做,但它极大地影响了修剪的质量。
这个排名非常直观。我们本可以将激活和梯度都用作排名方法。如果它们中的任何一个很高,则意味着它们对输出很重要。将它们相乘可以让我们有一种在梯度或激活非常低或很高时丢弃/保留过滤器的方法。
这让我很疑惑——他们是否将修剪问题提出为最小化网络成本差异,然后提出泰勒扩展方法,还是相反,而网络成本差异预言是支持他们的新方法的一种方法?:-)
在论文中,他们的方法在准确性方面也优于其他方法,因此看起来预言是一个很好的指标。
无论如何,我认为这是一种比粒子过滤器更易于编码和测试的好方法,所以我们将进一步探索这一点!
3、使用泰勒标准排名修剪猫与狗分类器
假设我们有一个迁移学习任务,需要从相对较小的数据集中创建分类器。就像在这篇 Keras 博客文章中一样。
我们可以使用像 VGG 这样的强大的预训练网络进行迁移学习,然后修剪网络吗?
如果在 VGG16 中学习到的许多特征都是关于汽车、人和房屋的 - 它们对简单的狗/猫分类器的贡献有多大?
我认为这是一种非常常见的问题。
作为训练集,我们将使用来自 Kaggle Dogs vs Cats 数据集的 1000 张猫图像和 1000 张狗图像。作为测试集,我们将使用 400 张猫图像和 400 张狗图像。
首先让我们展示一些统计数据:
- 准确率从 98.7% 下降到 97.5%。
- 网络大小从 538 MB 减小到 150 MB。
- 在 i7 CPU 上,单个图像推理时间从 0.78 秒缩短至 0.277 秒,几乎缩短了 3 倍!
3.1 训练大型网络
我们将采用 VGG16,删除完全连接的层,并添加三个新的完全连接的层。我们将冻结卷积层,并仅重新训练新的完全连接的层。在 PyTorch 中,新层如下所示:
self.classifier = nn.Sequential(
nn.Dropout(),
nn.Linear(25088, 4096),
nn.ReLU(inplace=True),
nn.Dropout(),
nn.Linear(4096, 4096),
nn.ReLU(inplace=True),
nn.Linear(4096, 2))经过 20 个数据增强训练后,我们在测试集上获得了 98.7% 的准确率。
3.2 排序滤波器
要计算泰勒标准,我们需要对数据集执行前向+后向传递(如果数据集太大,则对数据集的较小部分执行前向+后向传递。但由于我们只有 2000 张图像,因此我们使用这个)。
现在我们需要以某种方式获取卷积层的梯度和激活。在 PyTorch 中,我们可以在梯度计算上注册一个钩子,因此当它们准备就绪时会调用回调:
for layer, (name, module) in enumerate(self.model.features._modules.items()):
x = module(x)
if isinstance(module, torch.nn.modules.conv.Conv2d):
x.register_hook(self.compute_rank)
self.activations.append(x)
self.activation_to_layer[activation_index] = layer
activation_index += 1现在我们在 self.activations 中有了激活,当梯度准备就绪时,将调用 compute_rank:
def compute_rank(self, grad):
activation_index = len(self.activations) - self.grad_index - 1
activation = self.activations[activation_index]
values = \
torch.sum((activation * grad), dim = 0).\
sum(dim=2).sum(dim=3)[0, :, 0, 0].data
# Normalize the rank by the filter dimensions
values = \
values / (activation.size(0) * activation.size(2) * activation.size(3))
if activation_index not in self.filter_ranks:
self.filter_ranks[activation_index] = \
torch.FloatTensor(activation.size(1)).zero_().cuda()
self.filter_ranks[activation_index] += values
self.grad_index += 1这会将批次中的每个激活及其梯度逐点相乘,然后对于每个激活(即卷积的输出),我们在输出维度之外的所有维度上求和。
例如,如果批次大小为 32,特定激活的输出数量为 256,该激活的空间大小为 112x112,因此激活/梯度形状为 32x256x112x112,则输出将是一个 256 大小的向量,表示此层中 256 个滤波器的排名。
现在我们有了排名,我们可以使用最小堆来获取 N 个排名最低的滤波器。与 Nvidia 论文中在每次迭代中使用 N=1 不同,为了更快地获得结果,我们将使用 N=512!这意味着每次修剪迭代,我们都将从 4224 个卷积滤波器的原始数量中删除 12%。
低排名滤波器的分布很有趣。大部分被修剪的滤波器都来自更深的层。以下是第一次迭代后被修剪的滤波器:
| 层编号 | 修剪掉的滤波器数量 |
|---|---|
| Layer 0 | 6 |
| Layer 2 | 1 |
| Layer 5 | 4 |
| Layer 7 | 3 |
| Layer 10 | 23 |
| Layer 12 | 13 |
| Layer 14 | 9 |
| Layer 17 | 51 |
| Layer 19 | 35 |
| Layer 21 | 52 |
| Layer 24 | 68 |
| Layer 26 | 74 |
| Layer 28 | 73 |
3.3 微调并重复
在此阶段,我们解冻所有层并重新训练网络 10 个时期,这足以在此数据集上获得良好的结果。然后我们回到步骤 1,使用修改后的网络并重复。
这是我们付出的真正代价 - 这是用于训练网络的时期数的 50%,在一次迭代中。在这个玩具数据集中,我们可以侥幸逃脱,因为数据集很小。如果你对一个巨大的数据集这样做,你最好有很多 GPU。
4、结束语
我认为修剪是一种被忽视的方法,它将得到更多的关注和在实践中的使用。我们展示了如何在玩具数据集上获得良好的结果。我认为深度学习在实践中解决的许多问题与这个问题类似,在有限的数据集上使用迁移学习,因此它们也可以从修剪中受益。
原文链接:神经网络修剪实践 - BimAnt
