图论系列(dfs)9.25

一、主题空间
 

场地由若干主题空间与走廊组成，场地的地图记作由一维字符串型数组 grid，字符串中仅包含 "0"～"5" 这 6 个字符。地图上每一个字符代表面积为 1 的区域，其中 "0" 表示走廊，其他字符表示主题空间。相同且连续（连续指上、下、左、右四个方向连接）的字符组成同一个主题空间。

假如整个 grid 区域的外侧均为走廊。请问，不与走廊直接相邻的主题空间的最大面积是多少？如果不存在这样的空间请返回 0。

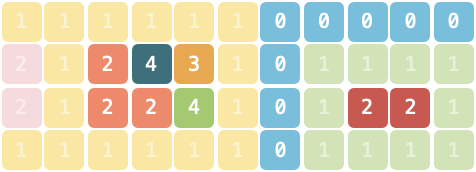
输入：grid = ["11111100000","21243101111","21224101221","11111101111"]

输出：3

解释：8 个主题空间中，有 5 个不与走廊相邻，面积分别为 3、1、1、1、2，最大面积为 3。

思路：

题目中要求不与走廊直接相邻的主题空间的最大面积。最外层和0都是走廊。

在dfs深搜的函数中:

第一种情况:如果x在第一行或者最后一行，或者y在第一列或者最后一列(这样就意味着与走廊直接相邻了)，count=-999999。

第二种情况:如果arr[x][y]=0,也代表与走廊直接相邻了，count=-999999;

        if (x == 0 || x == arr.length - 1 || y == 0 || y == arr[0].length - 1)
            count = -999999;

第三种情况: 相邻的点满足不与走廊相连，但是arr[x][y]!=target,这样count=-999999;

        if (x != 0) {
            if (arr[x - 1][y] == target) {
                count += dfs(x - 1, y, target);
            } else if (arr[x - 1][y] == 0) {
                count = -999999;
            }
        }

判断上下左右四个分支。(四叉树) 

代码：

class Solution {
    int[][] arr;
    public int largestArea(String[] grid) {
        arr = new int[grid.length][grid[0].length()];
        // 转换为int网格
        for (int i = 0; i < arr.length; i++) {
            String str = grid[i];
            for (int j = 0; j < arr[0].length; j++) {
                arr[i][j] = str.charAt(j) - '0';
            }
        }
        // dfs网格
        int res=0;
        for (int i = 1; i < arr.length; i++) {
            for (int j = 1; j < arr[0].length; j++) {
                if(arr[i][j]>0&&arr[i][j]<=5){
                    res=Math.max(res,dfs(i,j,arr[i][j]));
                }
            }
        }
        return res;
    }

    public int dfs(int x, int y, int target) {
        arr[x][y] = arr[x][y] * -1;
        int count = 1;
        // 先判断是否在边界
        if (x == 0 || x == arr.length - 1 || y == 0 || y == arr[0].length - 1)
            count = -999999;
        // 上边进行讨论
        if (x != 0) {
            if (arr[x - 1][y] == target) {
                count += dfs(x - 1, y, target);
            } else if (arr[x - 1][y] == 0) {
                count = -999999;
            }
        }
        // 下边进行讨论
        if (x != arr.length - 1) {
            if (arr[x + 1][y] == target) {
                count += dfs(x + 1, y, target);
            } else if (arr[x + 1][y] == 0) {
                count = -999999;
            }
        }
        // 左边进行讨论
        if (y != 0) {
            if (arr[x][y - 1] == target) {
                count += dfs(x, y - 1, target);
            } else if (arr[x][y - 1] == 0) {
                count = -999999;
            }
        }
        //
        if (y != arr[0].length-1) {
            if (arr[x][y + 1] == target) {
                count += dfs(x, y + 1, target);
            } else if (arr[x][y + 1] == 0) {
                count = -999999;
            }
        }
        return count;
    }
}

二、飞地的数量

给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个海洋单元格、1 表示一个陆地单元格。

一次 移动 是指从一个陆地单元格走到另一个相邻（上、下、左、右）的陆地单元格或跨过 grid 的边界。

返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。

示例 1：

输入：grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出：3
解释：有三个 1 被 0 包围。一个 1 没有被包围，因为它在边界上

思路:

我们可以将与边界相连的陆地都标记一下，因为与边界相连的陆地连通块是可以到达的。剩下的陆地就是无法到达边界的。

那么如何标记可以到达的陆地呢？我们可以遍历第一行、最后一行、第一列、最后一列的数，如果他们的值是1，就把值修改掉，然后继续dfs搜索。

代码：

class Solution {
    public int numEnclaves(int[][] grid) {
        //对第0行和第n-1行淹没
        for (int i = 0; i < grid[0].length; i++) {
            dfs(grid, 0, i);
            dfs(grid,grid.length-1,i);
        }
        //对第0列和第n-1列淹没
        for (int i = 0; i < grid.length; i++) {
            dfs(grid, i, 0);
            dfs(grid,i,grid[0].length-1);
        }
        int count=0;
        for(int i=0;i<grid.length;i++){
            for(int j=0;j<grid[0].length;j++){
                if(grid[i][j]==1)count++;
            }
        }
        return count;
    }

    public void dfs(int[][] grid,int x,int y){
        if(grid[x][y]==0)return;
        grid[x][y]=0;
        if(x>0)dfs(grid,x-1,y);
        if(x<grid.length-1)dfs(grid,x+1,y);
        if(y>0)dfs(grid,x,y-1);
        if(y<grid[0].length-1)dfs(grid,x,y+1);
    }
}