【算法题】221. 最大正方形-力扣(LeetCode)

【算法题】221. 最大正方形-力扣(LeetCode)

1.题目

下方是力扣官方题目的地址

221. 最大正方形

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例 1：

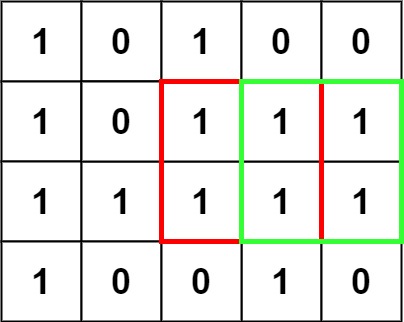
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

示例 2：

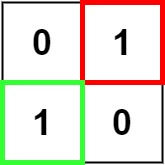
输入：matrix = [["0","1"],["1","0"]]
输出：1

示例 3：

输入：matrix = [["0"]]
输出：0

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 300
• matrix[i][j] 为 '0' 或 '1'

2.题解

思路

这题可以用动态规划来解决

这题的关键在于正确找到dp数组所代表的意义

一般的思路是想到用dp[i] [j]来表示这个区域中的最大正方形的边长。

不过我们仔细一想，这样子很难用动态规划来解决该问题。

所以我们不妨换个思路：

用dp[i] [j]代表以 (i,j) 为右下角，且只包含 1 的正方形的边长最大值。然后在dp[i] [j]中找到的最大值就是最大边长。

如果matrix[i] [j]=0的话，那么dp[i] [j] 为0；如果为1的话，那么至少也是1。至于能不能变大，就得向左上角扩伸。能够扩伸的前提是三个方向都需要能够扩伸，所以我们得取三个方向的dp的最小值，再加上一个1。

所以我们就可以得出状态转移方程：

dp[i][j]+=min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1

得出了转移方程，再考虑一些特殊值，这题 就可以解决了

Python代码

class Solution(object):
    def countSquares(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: int
        """
        n=len(matrix)
        m=len(matrix[0])
        ans=0
        dp=[[0]*m for _ in range(n)]
        for i in range(n):
            for j in range(m):
                if matrix[i][j]==1:
                    if i==0 or j==0:dp[i][j]=1  # 给特殊位置的“1”赋值
                    else:dp[i][j]+=min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1 # 正常位置的直接利用状态转移方程
                    ans+=dp[i][j]
        return ans

3.结语

本人资历尚浅，发博客主要是记录与学习，欢迎大佬们批评指教！大家也可以在评论区多多交流，相互学习，共同成长。