使用C++编写一个AVL的增删改查代码并附上代码解释
//qq460219753提供其他代码帮助
#include <iostream>
using namespace std;
struct Node
{
int data;
Node *left;
Node *right;
int height;
};
// 获取结点高度
int height(Node *node)
{
if (node == nullptr)
{
return 0;
}
return node->height;
}
// 获取两个数中较大的一个
int max(int a, int b)
{
return (a > b) ? a : b;
}
// 创建新结点
Node *newNode(int data)
{
Node *node = new Node();
node->data = data;
node->left = nullptr;
node->right = nullptr;
node->height = 1;
return node;
}
// 右旋操作
Node *rightRotate(Node *y)
{
Node *x = y->left;
Node *T2 = x->right;
// 进行旋转
x->right = y;
y->left = T2;
// 更新高度
y->height = max(height(y->left), height(y->right)) + 1;
x->height = max(height(x->left), height(x->right)) + 1;
// 返回新的根结点
return x;
}
// 左旋操作
Node *leftRotate(Node *x)
{
Node *y = x->right;
Node *T2 = y->left;
// 进行旋转
y->left = x;
x->right = T2;
// 更新高度
x->height = max(height(x->left), height(x->right)) + 1;
y->height = max(height(y->left), height(y->right)) + 1;
// 返回新的根结点
return y;
}
// 获取平衡因子
int getBalanceFactor(Node *node)
{
if (node == nullptr)
{
return 0;
}
return height(node->left) - height(node->right);
}
// 插入结点
Node *insert(Node *node, int data)
{
if (node == nullptr)
{
return newNode(data);
}
if (data < node->data)
{
node->left = insert(node->left, data);
}
else if (data > node->data)
{
node->right = insert(node->right, data);
}
else
{
return node;
}
// 更新高度
node->height = 1 + max(height(node->left), height(node->right));
// 获取平衡因子
int balanceFactor = getBalanceFactor(node);
// 左旋操作
if (balanceFactor > 1 && data < node->left->data)
{
return rightRotate(node);
}
// 右旋操作
if (balanceFactor < -1 && data > node->right->data)
{
return leftRotate(node);
}
// 左右旋操作
if (balanceFactor > 1 && data > node->left->data)
{
node->left = leftRotate(node->left);
return rightRotate(node);
}
// 右左旋操作
if (balanceFactor < -1 && data < node->right->data)
{
node->right = rightRotate(node->right);
return leftRotate(node);
}
// 返回不需要平衡的结点
return node;
}
// 获取最小值结点
Node *minValueNode(Node *node)
{
Node *current = node;
// 找到最左侧结点
while (current->left != nullptr)
{
current = current->left;
}
return current;
}
// 删除结点
Node *deleteNode(Node *root, int data)
{
if (root == nullptr)
{
return root;
}
// 寻找要删除的结点
if (data < root->data)
{
root->left = deleteNode(root->left, data);
}
else if (data > root->data)
{
root->right = deleteNode(root->right, data);
}
else
{
// 结点只有一个孩子结点或没有孩子结点
if ((root->left == nullptr) || (root->right == nullptr))
{
Node *temp = root->left ? root->left : root->right;
// 没有孩子结点的情况
if (temp == nullptr)
{
temp = root;
root = nullptr;
}
else
{
*root = *temp;
}
delete temp;
}
else
{
// 结点有两个孩子结点
Node *temp = minValueNode(root->right);
root->data = temp->data;
root->right = deleteNode(root->right, temp->data);
}
}
// 如果树中只有一个结点,则返回
if (root == nullptr)
{
return root;
}
// 更新高度
root->height = 1 + max(height(root->left), height(root->right));
// 获取平衡因子
int balanceFactor = getBalanceFactor(root);
// 左旋操作
if (balanceFactor > 1 && getBalanceFactor(root->left) >= 0)
{
return rightRotate(root);
}
// 右旋操作
if (balanceFactor < -1 && getBalanceFactor(root->right) <= 0)
{
return leftRotate(root);
}
// 左右旋操作
if (balanceFactor > 1 && getBalanceFactor(root->left) < 0)
{
root->left = leftRotate(root->left);
return rightRotate(root);
}
// 右左旋操作
if (balanceFactor < -1 && getBalanceFactor(root->right) > 0)
{
root->right = rightRotate(root->right);
return leftRotate(root);
}
// 返回不需要平衡的结点
return root;
}
// 查找结点
Node *search(Node *node, int data)
{
if (node == nullptr || node->data == data)
{
return node;
}
if (node->data < data)
{
return search(node->right, data);
}
return search(node->left, data);
}
// 中序遍历
void inorder(Node *root)
{
if (root != nullptr)
{
inorder(root->left);
cout << root->data << " ";
inorder(root->right);
}
}
int main()
{
Node *root = nullptr;
// 插入结点
root = insert(root, 10);
root = insert(root, 20);
root = insert(root, 30);
root = insert(root, 40);
root = insert(root, 50);
root = insert(root, 25);
// 中序遍历树
cout << "Inorder traversal of the AVL tree is: " << endl;
inorder(root);
cout << endl;
// 删除结点
root = deleteNode(root, 25);
// 中序遍历树
cout << "Inorder traversal of the AVL tree after deleting 25 is: " << endl;
inorder(root);
cout << endl;
return 0;
}
运行结果如下
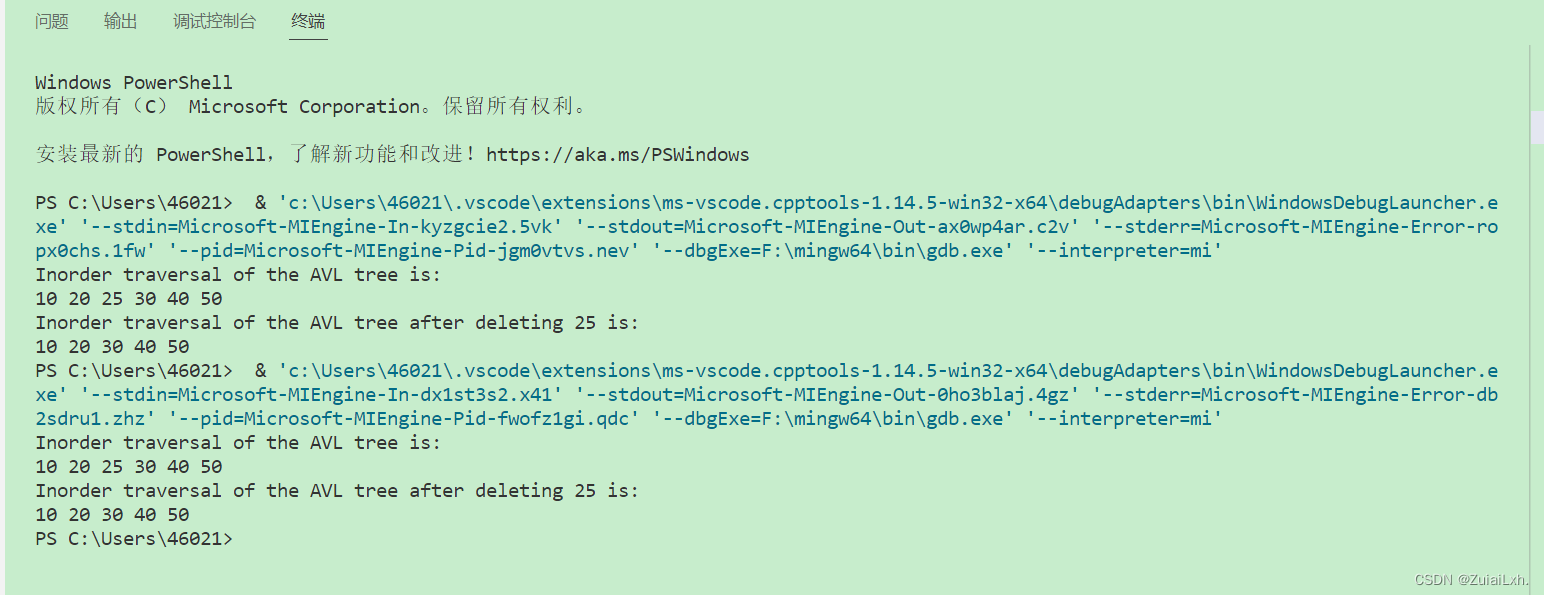
代码解释:
Node 结构体定义:定义了 AVL 树结点的数据结构。
height 函数:用于获取结点的高度,如果结点为空则返回 -1。
getBalanceFactor 函数:用于获取结点的平衡因子,平衡因子为左子树的高度减去右子树的高度。
leftRotate 函数:用于左旋操作。
rightRotate 函数:用于右旋操作。
insert 函数:用于插入结点。首先进行普通的二叉搜索树插入操作,然后对树进行平衡操作。
minValueNode 函数:用于获取 AVL 树中最小的结点。
deleteNode 函数:用于删除结点。首先进行普通的二叉搜索树删除操作,然后对树进行平衡操作。
search 函数:用于查找结点。
inorder 函数:用于中序遍历 AVL 树。
main 函数:创建 AVL 树,插入结点,进行中序遍历,删除结点,再次进行中序遍历。
