十二届蓝桥杯省赛c++(下)
1、

拿到题目一定要读懂题意,不要看到这题目就上来模拟什么闰年,一月的天数啥的。这个题目问你当天的时间,就说明年月日跟你都没关系,直接无视就好了。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
using namespace std;
#define ll long long//能开long long就开,避免爆数据
int main()
{
ll n;
cin >> n;
n /= 1000;//先把毫秒转化为秒
ll hour = (n / 60 / 60) % 24;//求出小时数,一定要记得取模
ll minute = (n % 3600 / 60) % 60;//分钟数
ll s = n % 3600 % 60;//秒数
if (hour < 10) cout << 0;//记得处理好零的输出
cout << hour << ':';
if (minute < 10) cout << 0;
cout << minute << ':';
if (s < 10) cout << 0;
cout << s;
return 0;
}2、
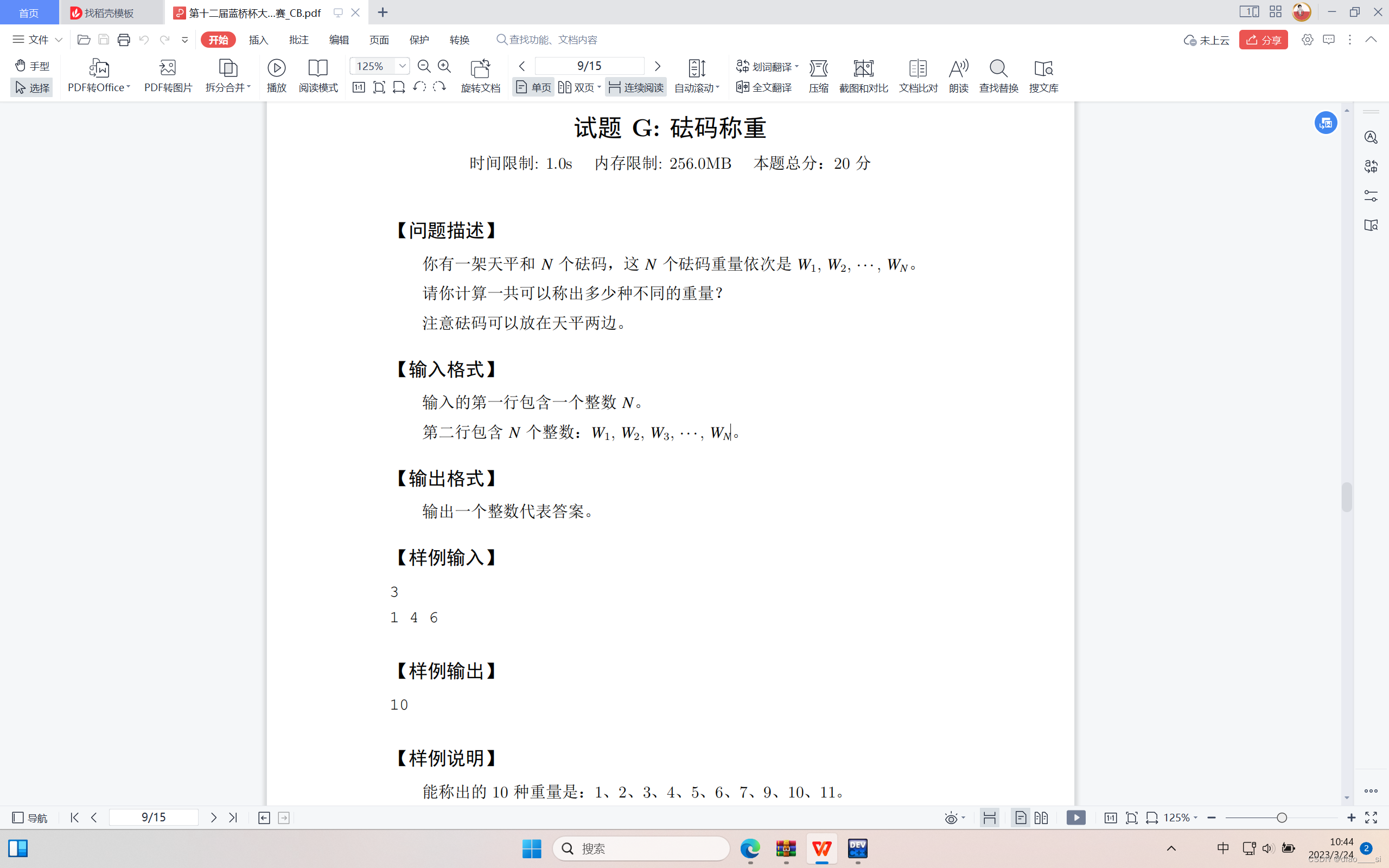
(1)动态规划:
闫氏dp分析法:
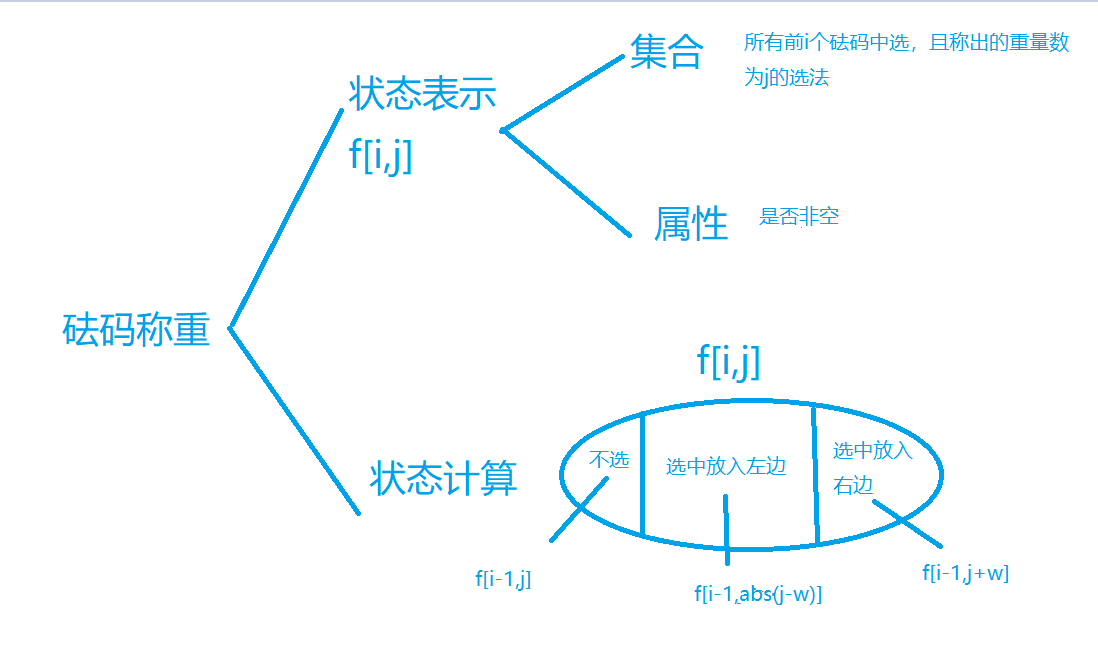
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
#define N 1010000
int f[150][N] ,n ,w[N] ,ans ,sum;
int main()
{
cin >> n;
for (int i = 1 ;i <= n ;i ++) cin >> w[i] ,sum += w[i];//拿sum存储砝码的重量之和
f[0][0] = 1;//初始化,零个砝码测出质量为0的方案有一个
for (int i = 1 ;i <= n ;i ++)
{
for (int j = 0 ;j <= sum ;j ++)
{
f[i][j] = f[i - 1][j];//第i个砝码没有用
f[i][j] += f[i - 1][abs(j - w[i])];//第i个砝码放左边
f[i][j] += f[i - 1][j + w[i]];//第i个砝码放右边
}
}
for (int i = 1 ;i <= sum ;i ++)
if (f[n][i]) ans ++;//如果有值,说明前n个砝码可以测出来重量为i的物品,答案加一
cout << ans;
return 0;
}(2)dfs暴力,拿一半分
如果这道题实在没时间做或者说想不到思路,那么我们就可以考虑暴力拿分
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
#define N 1010000
int n ,w[N] ,ans;
bool vis[N];
void dfs(int k ,int g)
{
if (k > n)
{
if (g > 0 && !vis[g])
{
ans ++;
vis[g] = true;
}
return;
}
dfs(k + 1 ,g);
dfs(k + 1 ,g + w[k]);
dfs(k + 1 ,abs(g - w[k]));
}
int main()
{
cin >> n;
for (int i = 1 ;i <= n ;i ++)
{
cin >> w[i];
}
dfs(0 ,0);
cout << ans;
return 0;
}3、
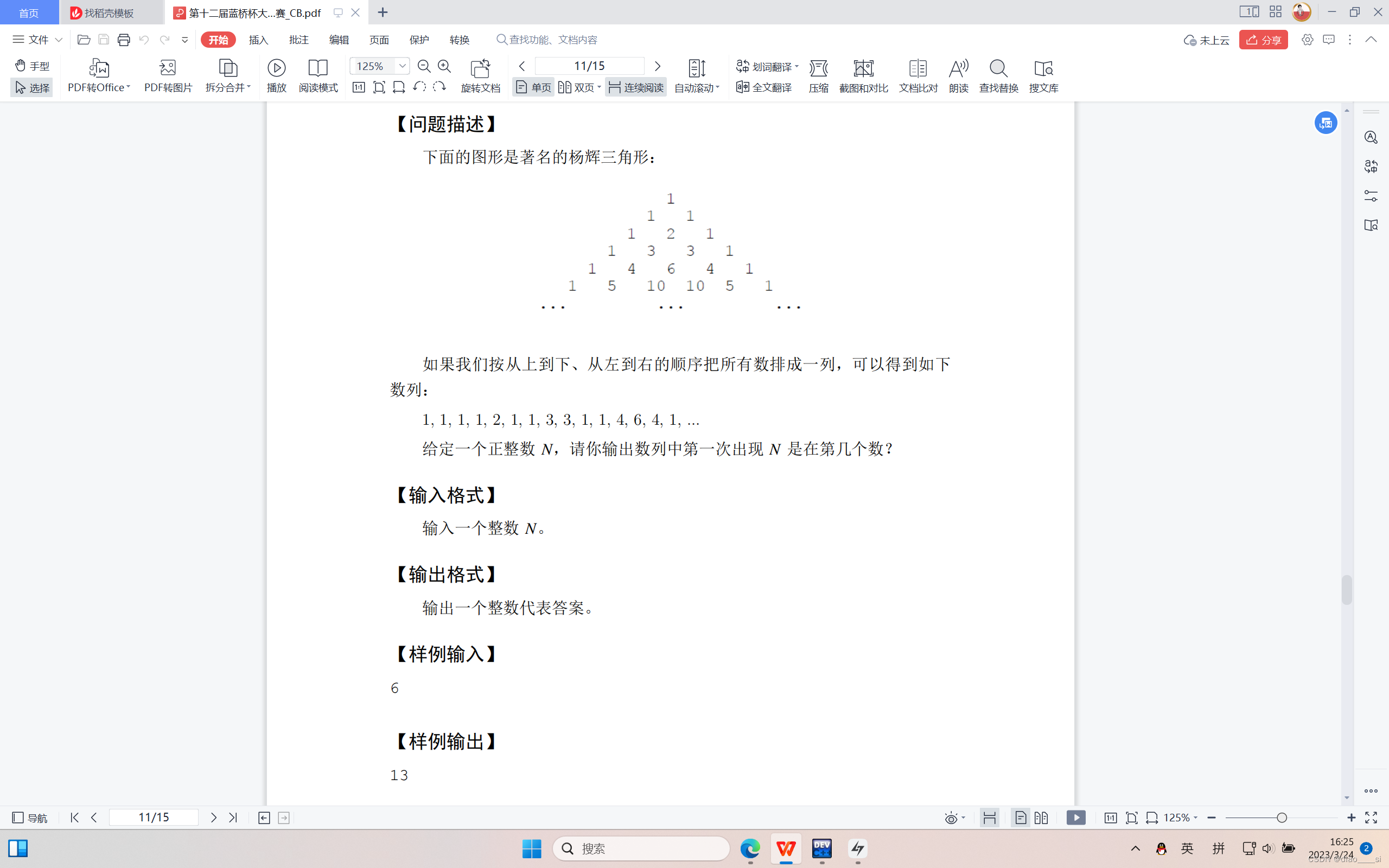
这一届的题目从这一题开始往后,难度就起来了。
1、先说暴力做法吧,可以拿四十分,直接预处理一千行
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1e3 + 10;
int n = 1000;
int a[N][N];
int main() {
a[1][1] = 1;
for (int i = 2; i <= n; i ++) // 预处理
for (int j = 1; j <= i; j ++)
a[i][j] = a[i - 1][j] + a[i - 1][j - 1];
int x; cin >> x;
int cnt = 0;
for (int i = 1; i <= n; i ++) // 枚举
for (int j = 1; j <= i; j ++) {
cnt ++;
if (a[i][j] == x) {
cout << cnt;
return 0;
}
}
return 0;
}
2、正解
关于这道题我们需要明白:杨辉三角其实就是组合数!如图:
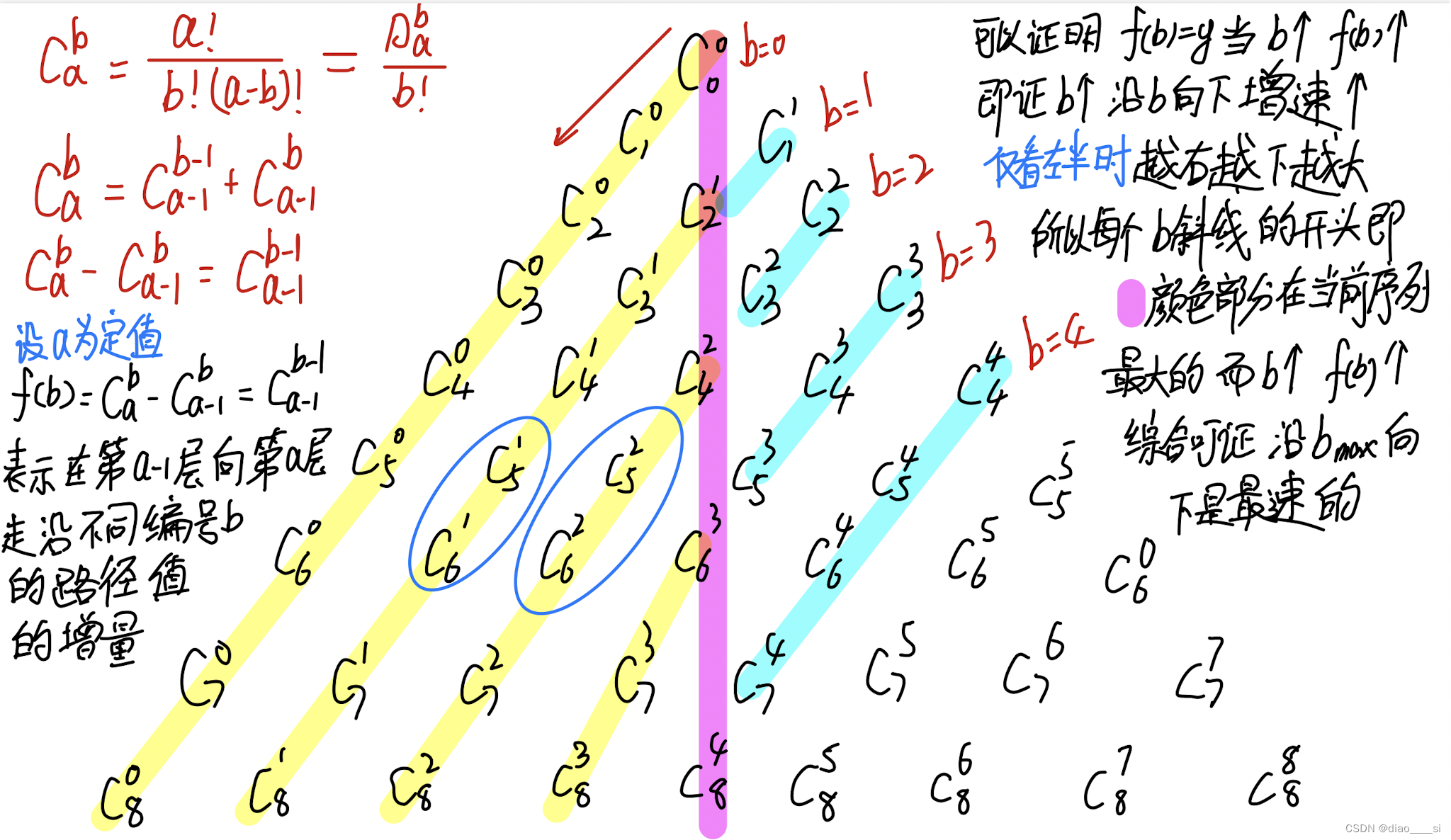
从图中我们可以观察出两个性质:
1、以中间的紫色分割线为界,左右两边的数值是相等的。那么右边存在的某一个值左边一定也存在,并且根据题目的排序方式来看左边相对而言更加靠前,也就是说某一个数N第一次一定是在左边先出现。因此,我们要找的结果一定是在左边部分中。
2、中间一列数从上往下是在递增的,每一横排从左往右也在递增,每一斜行从上往下也在递增。所以每个斜行都保持了单调性。
现在知道了这两个性质,我们可以想想怎么从左边中找到N。直接枚举的复杂度太高,不可取,而根据第二条中所提到的单调性,我们可以很自然的想到二分法。那么该如何二分?竖着?横着?这都不可取,因为不论是哪一种我们都无从下手。所以我们需要斜着来!每一个斜行从紫色部分开始,也就是C(k,2*k)的形式,到C(k ,n)结束(为什么从n结束?可以思考一下,倘若想不明白可以私信问我)。由于n最大1e9,C(34, 17) > 1e9, C(32, 16) < 1e9,因此只要枚举前16个斜行即可。
C(k, r)对应的顺序值为:(r + 1) * r / 2 + k + 1
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
using namespace std;
#define ll long long
ll n;
ll c(int a ,int b)
{
ll res = 1;
for (int i = a ,j = 1 ;j <= b ;i -- ,j ++)//求组合数的过程
{
res = res * i / j;
if (res > n) return res;//如果res已经大于n就不用在求了,肯定不是答案,直接返回。这样也可以避免爆数据
}
return res;
}
bool h(int k)
{
int l = 2 * k ,r = n;
while (l < r)
{
ll mid = (l + r) / 2;
if (c(mid ,k) >= n) r = mid;
else
l = mid + 1;
}
if (c(l ,k) != n) return false;
cout << 1ll * (l + 1) * l / 2 + k + 1;//如果找到了,输出位置
return true;
}
int main()
{
cin >> n;
for (int i = 16 ; ;i --)//枚举前十六个斜行
if (h(i)) break;
return 0;
}
4、
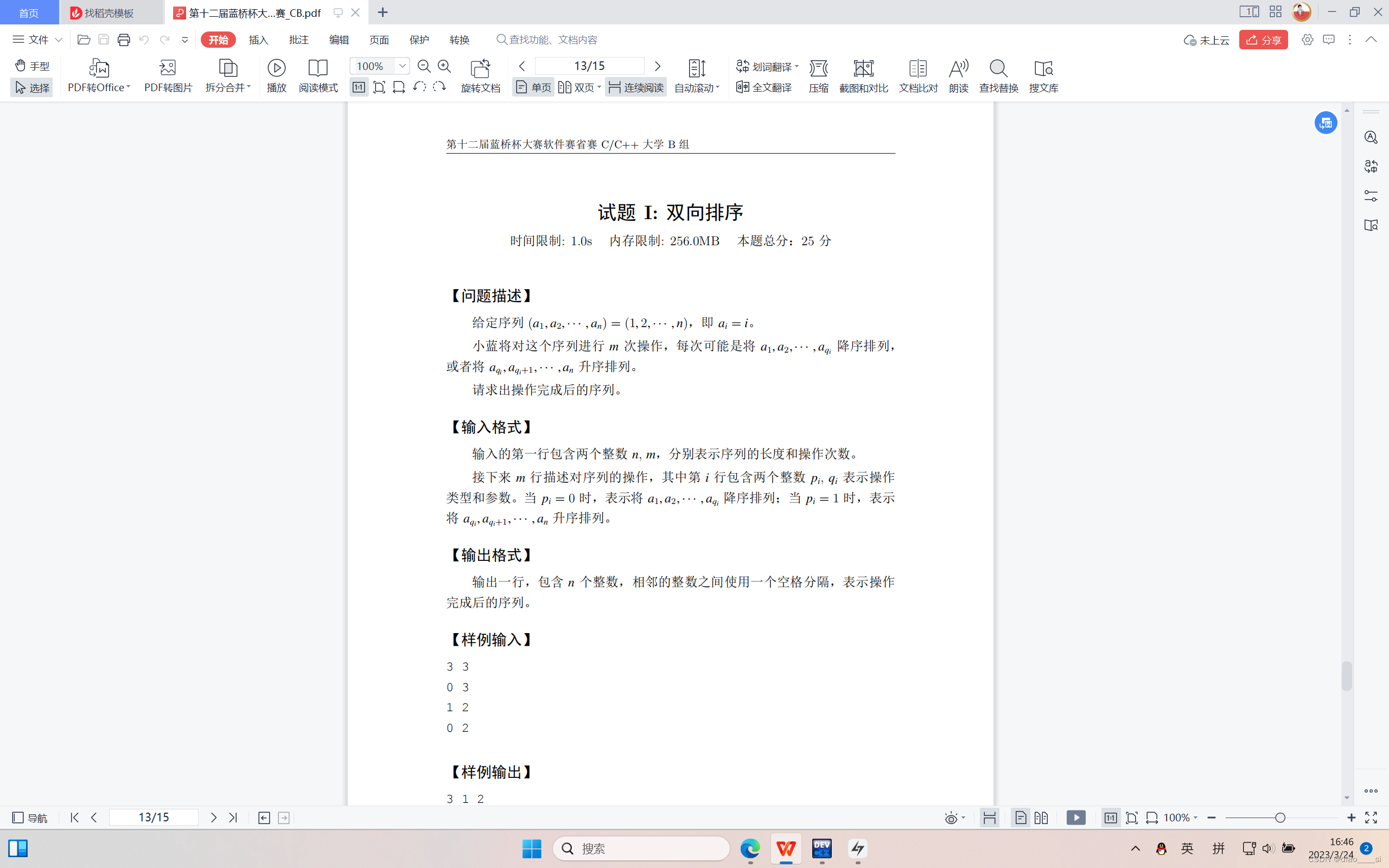
我也不会。。。
5、
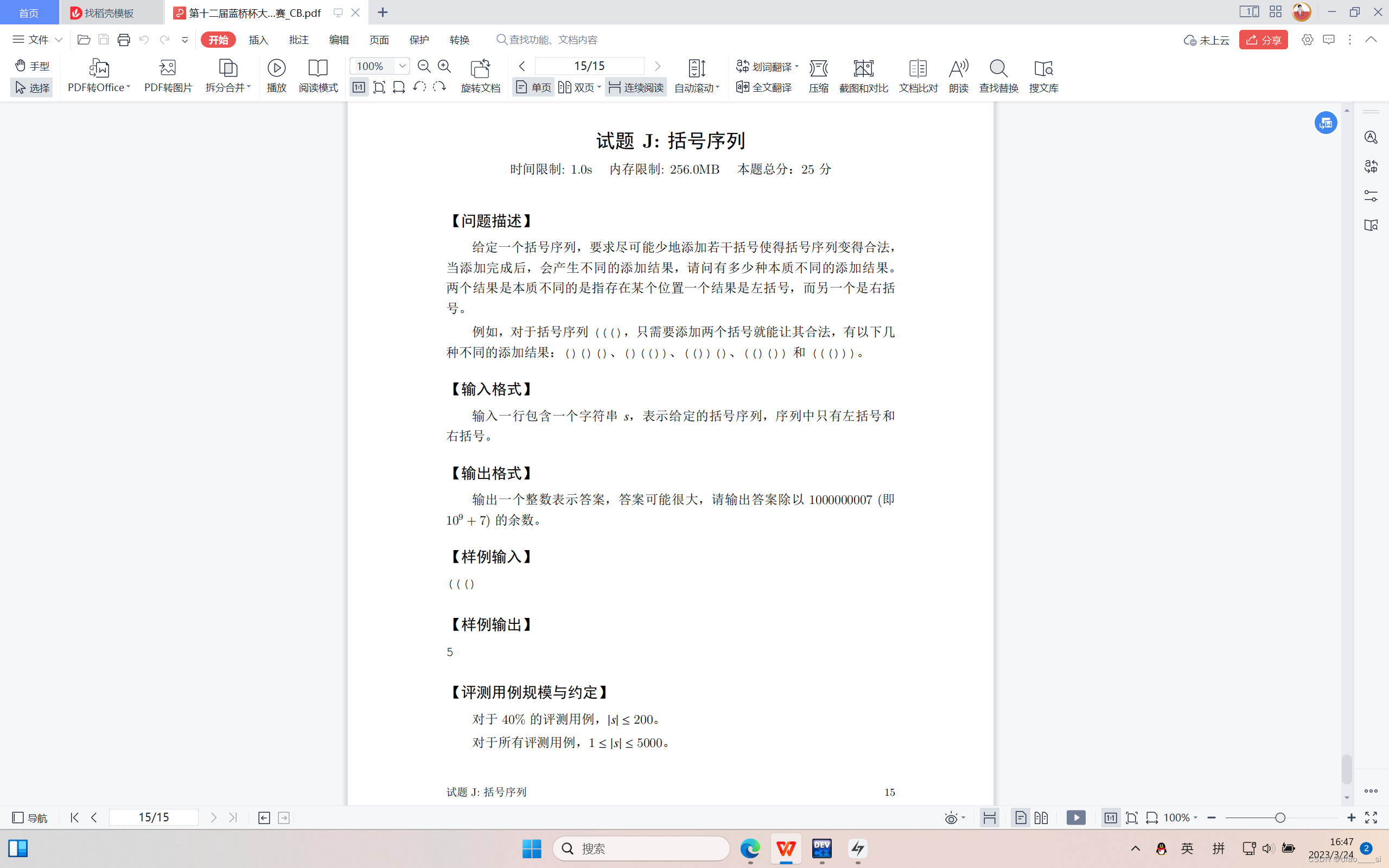
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
using namespace std;
#define ll long long
#define N 5500
const int mod = 1000000007;
ll f[N][N] ,len;
char s[N];
ll hu()
{
memset(f ,0 ,sizeof(f));
f[0][0] = 1;
for (int i = 1 ;i <= len ;i ++)
{
if (s[i] == '(')
{
for (int j = 1 ;j <= len ;j ++)
f[i][j] = f[i - 1][j - 1];
}
else
{
f[i][0] = (f[i - 1][0] + f[i - 1][1]) % mod;
for (int j = 1 ;j <= len ;j ++)
f[i][j] = (f[i - 1][j + 1] + f[i][j - 1]) % mod;
}
}
for (int i = 0 ;i <= len ;i ++)
if (f[len][i]) return f[len][i];
return -1;
}
int main()
{
scanf("%s" ,s + 1);
len = strlen(s + 1);
ll l = hu();
reverse(s + 1 ,s + len + 1);
for (int i = 1 ;i <= len ; i ++)
{
if (s[i] == '(') s[i] = ')';
else
s[i] = '(';
}
ll r = hu();
printf("%lld" ,l * r % mod);
return 0;
}
