51c深度学习~合集6
我自己的原文哦~ https://blog.51cto.com/whaosoft/12369516
#卷积神经网络压缩方法总结
本文介绍了卷积网络压缩的常见方法:低秩近似、剪枝与稀疏约束、参数量化、二值化网络、知识蒸馏和浅层/轻量网络。
我们知道,在一定程度上,网络越深,参数越多,模型越复杂,其最终效果越好。神经网络的压缩算法是,旨在将一个庞大而复杂的预训练模型(pre-trained model)转化为一个精简的小模型。按照压缩过程对网络结构的破坏程度,我们将模型压缩技术分为“前端压缩”和“后端压缩”两部分。
前端压缩,是指在不改变原网络结构的压缩技术,主要包括知识蒸馏、紧凑的模型结构涉及以及滤波器(filter)层面的剪枝等。
后端压缩,是指包括低秩近似、未加限制的剪枝、参数量化以及二值网络等,目标在于尽可能减少模型大小,会对原始网络结构造成极大程度的改造。
总结:前端压缩几乎不改变原有网络结构(仅仅只是在原模型基础上减少了网络的层数或者滤波器个数),后端压缩对网络结构有不可逆的大幅度改变,造成原有深度学习库、甚至硬件设备不兼容改变之后的网络。其维护成本很高。
1. 低秩近似
简单理解就是,卷积神经网络的权重矩阵往往稠密且巨大,从而计算开销大,有一种办法是采用低秩近似的技术将该稠密矩阵由若干个小规模矩阵近似重构出来,这种方法归类为低秩近似算法。
一般地,行阶梯型矩阵的秩等于其“台阶数”----非零行的行数。
低秩近似算法能减小计算开销的原理如下:

基于以上想法, Sindhwani 等人提出使用结构化矩阵来进行低秩分解的算法, 具体原理可自行参考论文。另一种比较简便的方法 是使用矩阵分解来降低权重矩阵的参数, 如 Denton 等人提出使用奇异值分解(Singular Value Decomposition, 简称 SVD)分解 来重构全连接层的权重。
1.1 总结
低秩近似算法在中小型网络模型上,取得了很不错的效果,但其超参数量与网络层数呈线性变化趋势,随着网络层数的增加与模型复杂度的提升,其搜索空间会急剧增大,目前主要是学术界在研究,工业界应用不多。
2. 剪枝与稀疏约束
给定一个预训练好的网络模型,常用的剪枝算法一般都遵从如下操作:
衡量神经元的重要程度。
移除掉一部分不重要的神经元,这步比前 1 步更加简便,灵活性更高。
对网络进行微调,剪枝操作不可避免地影响网络的精度,为防止对分类性能造成过大的破坏,需要对剪枝后的模型进行微调。对于大规模行图像数据集(如ImageNet)而言,微调会占用大量的计算资源,因此对网络微调到什么程度,是需要斟酌的。
返回第一步,循环进行下一轮剪枝。
基于以上循环剪枝框架,不同学者提出了不同的方法,Han等人提出首先将低于某个阈值的权重连接全部剪除,之后对剪枝后的网络进行微调以完成参数更新的方法,这种方法的不足之处在于,剪枝后的网络是非结构化的,即被剪除的网络连接在分布上,没有任何连续性,这种稀疏的结构,导致CPU高速缓冲与内存频繁切换,从而限制了实际的加速效果。
基于此方法,有学者尝试将剪枝的粒度提升到整个滤波器级别,即丢弃整个滤波器,但是如何衡量滤波器的重要程度是一个问题,其中一种策略是基于滤波器权重本身的统计量,如分别计算每个滤波器的 L1 或 L2 值,将相应数值大小作为衡量重要程度标准。
利用稀疏约束来对网络进行剪枝也是一个研究方向,其思路是在网络的优化目标中加入权重的稀疏正则项,使得训练时网络的部分权重趋向于 0 ,而这些 0 值就是剪枝的对象。
2.1 总结
总体而言,剪枝是一项有效减小模型复杂度的通用压缩技术,其关键之处在于如何衡量个别权重对于整体模型的重要程度。剪枝操作对网络结构的破坏程度极小,将剪枝与其他后端压缩技术相结合,能够达到网络模型最大程度压缩,目前工业界有使用剪枝方法进行模型压缩的案例。
3. 参数量化
相比于剪枝操作,参数量化则是一种常用的后端压缩技术。所谓“量化”,是指从权重中归纳出若干“代表”,由这些“代表”来表示某一类权重的具体数值。“代表”被存储在码本(codebook)之中,而原权重矩阵只需记录各自“代表”的索引即可,从而极大地降低了存储开销。这种思想可类比于经典的词包模型(bag-of-words model)。常用量化算法如下:
标量量化(scalar quantization)。
标量量化会在一定程度上降低网络的精度,为避免这个弊端,很多算法考虑结构化的向量方法,其中一种是乘积向量(Product Quantization, PQ),详情咨询查阅论文。
以PQ方法为基础,Wu等人设计了一种通用的网络量化算法:QCNN(quantized CNN),主要思想在于Wu等人认为最小化每一层网络输出的重构误差,比最小化量化误差更有效。

这三类基于聚类的参数量化算法,其本质思想在于将多个权重映射到同一个数值,从而实现权重共享,降低存储开销的目的。
3.1 总结
参数量化是一种常用的后端压缩技术,能够以很小的性能损失实现模型体积的大幅下降,不足之处在于,量化的网络是“固定”的,很难对其做任何改变,同时这种方法通用性差,需要配套专门的深度学习库来运行网络。
4. 二值化网络

def residual_unit(data, num_filter, stride, dim_match, num_bits=1):
"""残差块 Residual Block 定义
"""
bnAct1 = bnn.BatchNorm(data=data, num_bits=num_bits)
conv1 = bnn.Convolution(data=bnAct1, num_filter=num_filter, kernel=(3, 3), stride=stride, pad=(1, 1))
convBn1 = bnn.BatchNorm(data=conv1, num_bits=num_bits)
conv2 = bnn.Convolution(data=convBn1, num_filter=num_filter, kernel=(3, 3), stride=(1, 1), pad=(1, 1))
if dim_match:
shortcut = data
else:
shortcut = bnn.Convolution(data=bnAct1, num_filter=num_filter, kernel=(3, 3), stride=stride, pad=(1, 1))
return conv2 + shortcut4.1 二值网络的梯度下降
现在的神经网络几乎都是基于梯度下降算法来训练的,但是二值网络的权重只有±1,无法直接计算梯度信息,也无法进行权重更新。为解决这个问题,Courbariaux 等人提出二值连接(binary connect)算法,该算法采取单精度与二值结合的方式来训练二值神经网络(),这是第一次给出了关于如何对网络进行二值化和如何训练二值化神经网络的方法。过程如下:
权重 weight 初始化为浮点
前向传播 Forward Pass:-利用决定化方式(sign(x)函数)把 Weight 量化为 +1/-1, 以0为阈值- 利用量化后的 Weight (只有+1/-1)来计算前向传播,由二值权重与输入进行卷积运算(实际上只涉及加法),获得卷积层输出。
反向传播 Backward Pass:把梯度更新到浮点的 Weight 上(根据放松后的符号函数,计算相应梯度值,并根据该梯度的值对单精度的权重进行参数更新);训练结束:把 Weight 永久性转化为 +1/-1, 以便 inference 使用。
4.2 两个问题
网络二值化需要解决两个问题:如何对权重进行二值化和如何计算二值权重的梯度。

4.3 二值连接算法改进

可以看到的是权重二值化神经网络(BWN)和全精度神经网络的精确度几乎一样,但是与异或神经网络(XNOR-Net)相比而言,Top-1 和 Top-5 都有 10+% 的损失。
相比于权重二值化神经网络,异或神经网络将网络的输入也转化为二进制值,所以,异或神经网络中的乘法加法 (Multiplication and ACcumulation) 运算用按位异或 (bitwise xnor) 和数 1 的个数 (popcount) 来代替。
更多内容,可以看这两篇文章:
https://github.com/Ewenwan/MVision/tree/master/CNN/Deep_Compression/quantization/BNN
4.4 二值网络设计注意事项
不要使用 kernel = (1, 1) 的 Convolution (包括 resnet 的 bottleneck):二值网络中的 weight 都为 1bit, 如果再是 1x1 大小, 会极大地降低表达能力
增大 Channel 数目 + 增大 activation bit 数 要协同配合:如果一味增大 channel 数, 最终 feature map 因为 bit 数过低, 还是浪费了模型容量。同理反过来也是。
建议使用 4bit 及以下的 activation bit,过高带来的精度收益变小,而会显著提高 inference 计算量
5.知识蒸馏
本文只简单介绍这个领域的开篇之作-Distilling the Knowledge in a Neural Network,这是蒸 "logits"方法,后面还出现了蒸 "features" 的论文。想要更深入理解,中文博客可参考这篇文章-知识蒸馏是什么?一份入门随笔(https://zhuanlan.zhihu.com/p/90049906)。
知识蒸馏(knowledge distillation)(https://arxiv.org/abs/1503.02531),是迁移学习(transfer learning)的一种,简单来说就是训练一个大模型(teacher)和一个小模型(student),将庞大而复杂的大模型学习到的知识,通过一定技术手段迁移到精简的小模型上,从而使小模型能够获得与大模型相近的性能。

所以,可以知道 student 模型最终的损失函数由两部分组成:
第一项是由小模型(student 模型)的预测结果与大模型的“软标签”所构成的交叉熵(cross entroy);
第二项为小模型预测结果与普通类别标签的交叉熵。
这两个损失函数的重要程度可通过一定的权重进行调节,在实际应用中, T 的取值会影响最终的结果,一般而言,较大的 T 能够获得较高的准确度,T(蒸馏温度参数) 属于知识蒸馏模型训练超参数的一种。T 是一个可调节的超参数、T 值越大、概率分布越软(论文中的描述),曲线便越平滑,相当于在迁移学习的过程中添加了扰动,从而使得学生网络在借鉴学习的时候更有效、泛化能力更强,这其实就是一种抑制过拟合的策略。知识蒸馏的整个过程如下图:

student 模型的实际模型结构和小模型一样,但是损失函数包含了两部分,分类网络的知识蒸馏 mxnet 代码示例如下:
# -*-coding-*- : utf-8
"""
本程序没有给出具体的模型结构代码,主要给出了知识蒸馏 softmax 损失计算部分。
"""
import mxnet as mx
def get_symbol(data, class_labels, resnet_layer_num,Temperature,mimic_weight,num_classes=2):
backbone = StudentBackbone(data) # Backbone 为分类网络 backbone 类
flatten = mx.symbol.Flatten(data=conv1, name="flatten")
fc_class_score_s = mx.symbol.FullyConnected(data=flatten, num_hidden=num_classes, name='fc_class_score')
softmax1 = mx.symbol.SoftmaxOutput(data=fc_class_score_s, label=class_labels, name='softmax_hard')
import symbol_resnet # Teacher model
fc_class_score_t = symbol_resnet.get_symbol(net_depth=resnet_layer_num, num_class=num_classes, data=data)
s_input_for_softmax=fc_class_score_s/Temperature
t_input_for_softmax=fc_class_score_t/Temperature
t_soft_labels=mx.symbol.softmax(t_input_for_softmax, name='teacher_soft_labels')
softmax2 = mx.symbol.SoftmaxOutput(data=s_input_for_softmax, label=t_soft_labels, name='softmax_soft',grad_scale=mimic_weight)
group=mx.symbol.Group([softmax1,softmax2])
group.save('group2-symbol.json')
return grouptensorflow代码示例如下:
# 将类别标签进行one-hot编码
one_hot = tf.one_hot(y, n_classes,1.0,0.0) # n_classes为类别总数, n为类别标签
# one_hot = tf.cast(one_hot_int, tf.float32)
teacher_tau = tf.scalar_mul(1.0/args.tau, teacher) # teacher为teacher模型直接输出张量, tau为温度系数T
student_tau = tf.scalar_mul(1.0/args.tau, student) # 将模型直接输出logits张量student处于温度系数T
objective1 = tf.nn.sigmoid_cross_entropy_with_logits(student_tau, one_hot)
objective2 = tf.scalar_mul(0.5, tf.square(student_tau-teacher_tau))
"""
student模型最终的损失函数由两部分组成:
第一项是由小模型的预测结果与大模型的“软标签”所构成的交叉熵(cross entroy);
第二项为预测结果与普通类别标签的交叉熵。
"""
tf_loss = (args.lamda*tf.reduce_sum(objective1) + (1-args.lamda)*tf.reduce_sum(objective2))/batch_sizetf.scalar_mul 函数为对 tf 张量进行固定倍率 scalar 缩放函数。一般 T 的取值在 1 - 20 之间,这里我参考了开源代码,取值为 3。我发现在开源代码中 student 模型的训练,有些是和 teacher 模型一起训练的,有些是 teacher 模型训练好后直接指导 student 模型训练。
6. 浅层/轻量网络
浅层网络:通过设计一个更浅(层数较少)结构更紧凑的网络来实现对复杂模型效果的逼近, 但是浅层网络的表达能力很难与深层网络相匹敌。因此,这种设计方法的局限性在于只能应用解决在较为简单问题上。如分类问题中类别数较少的 task。
轻量网络:使用如 MobilenetV2、ShuffleNetv2 等轻量网络结构作为模型的 backbone可以大幅减少模型参数数量。
#不平衡数据集~建模の技巧和策略
这里讲述处理不平衡数据集和提高机器学习模型性能的各种技巧和策略,涵盖的一些技术包括重采样技术、代价敏感学习、使用适当的性能指标、集成方法和其他策略。都是py代码哦~~ 写的很狂飙~~
不平衡数据集是指一个类中的示例数量与另一类中的示例数量显著不同的情况。例如在一个二元分类问题中,一个类只占总样本的一小部分,这被称为不平衡数据集。类不平衡会在构建机器学习模型时导致很多问题。

不平衡数据集的主要问题之一是模型可能会偏向多数类,从而导致预测少数类的性能不佳。这是因为模型经过训练以最小化错误率,并且当多数类被过度代表时,模型倾向于更频繁地预测多数类。这会导致更高的准确率得分,但少数类别得分较低。
另一个问题是,当模型暴露于新的、看不见的数据时,它可能无法很好地泛化。这是因为该模型是在倾斜的数据集上训练的,可能无法处理测试数据中的不平衡。
在本文中,我们将讨论处理不平衡数据集和提高机器学习模型性能的各种技巧和策略。将涵盖的一些技术包括重采样技术、代价敏感学习、使用适当的性能指标、集成方法和其他策略。通过这些技巧,可以为不平衡的数据集构建有效的模型。
处理不平衡数据集的技巧
重采样技术是处理不平衡数据集的最流行方法之一。这些技术涉及减少多数类中的示例数量或增加少数类中的示例数量。
欠采样可以从多数类中随机删除示例以减小其大小并平衡数据集。这种技术简单易行,但会导致信息丢失,因为它会丢弃一些多数类示例。
过采样与欠采样相反,过采样随机复制少数类中的示例以增加其大小。这种技术可能会导致过度拟合,因为模型是在少数类的重复示例上训练的。
SMOTE是一种更高级的技术,它创建少数类的合成示例,而不是复制现有示例。这种技术有助于在不引入重复项的情况下平衡数据集。
代价敏感学习(Cost-sensitive learning)是另一种可用于处理不平衡数据集的技术。在这种方法中,不同的错误分类成本被分配给不同的类别。这意味着与错误分类多数类示例相比,模型因错误分类少数类示例而受到更严重的惩罚。
在处理不平衡的数据集时,使用适当的性能指标也很重要。准确性并不总是最好的指标,因为在处理不平衡的数据集时它可能会产生误导。相反,使用 AUC-ROC等指标可以更好地指示模型性能。
集成方法,例如 bagging 和 boosting,也可以有效地对不平衡数据集进行建模。这些方法结合了多个模型的预测以提高整体性能。Bagging 涉及独立训练多个模型并对它们的预测进行平均,而 boosting 涉及按顺序训练多个模型,其中每个模型都试图纠正前一个模型的错误。
重采样技术、成本敏感学习、使用适当的性能指标和集成方法是一些技巧和策略,可以帮助处理不平衡的数据集并提高机器学习模型的性能。
在不平衡数据集上提高模型性能的策略
收集更多数据是在不平衡数据集上提高模型性能的最直接策略之一。通过增加少数类中的示例数量,模型将有更多信息可供学习,并且不太可能偏向多数类。当少数类中的示例数量非常少时,此策略特别有用。
生成合成样本是另一种可用于提高模型性能的策略。合成样本是人工创建的样本,与少数类中的真实样本相似。这些样本可以使用 SMOTE等技术生成,该技术通过在现有示例之间进行插值来创建合成示例。生成合成样本有助于平衡数据集并为模型提供更多示例以供学习。
使用领域知识来关注重要样本也是一种可行的策略,通过识别数据集中信息量最大的示例来提高模型性能。例如,如果我们正在处理医学数据集,可能知道某些症状或实验室结果更能表明某种疾病。通过关注这些例子可以提高模型准确预测少数类的能力。
最后可以使用异常检测等高级技术来识别和关注少数类示例。这些技术可用于识别与多数类不同且可能是少数类示例的示例。这可以通过识别数据集中信息量最大的示例来帮助提高模型性能。
在收集更多数据、生成合成样本、使用领域知识专注于重要样本以及使用异常检测等先进技术是一些可用于提高模型在不平衡数据集上的性能的策略。这些策略可以帮助平衡数据集,为模型提供更多示例以供学习,并识别数据集中信息量最大的示例。
不平衡数据集的练习
这里我们使用信用卡欺诈分类的数据集演示处理不平衡数据的方法
import pandas as pd
import numpy as np
from sklearn.preprocessing import RobustScaler
from sklearn.linear\_model import LogisticRegression
from sklearn.model\_selection import train\_test\_split
from sklearn.metrics import accuracy\_score
from sklearn.metrics import confusion\_matrix, classification\_report,f1\_score,recall\_score,roc\_auc\_score, roc\_curve
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib import rc,rcParams
import itertools
import warnings
warnings.filterwarnings\("ignore", category\=DeprecationWarning\)
warnings.filterwarnings\("ignore", category\=FutureWarning\)
warnings.filterwarnings\("ignore", category\=UserWarning\)读取数据:
df \= pd.read\_csv\("creditcard.csv"\)
df.head\(\)
print\("Number of observations : " ,len\(df\)\)
print\("Number of variables : ", len\(df.columns\)\)
#Number of observations : 284807
#Number of variables : 31查看数据集信息:
df.info\(\)
\<class 'pandas.core.frame.DataFrame'\>
RangeIndex: 284807 entries, 0 to 284806
Data columns \(total 31 columns\):
\# Column Non-Null Count Dtype
\--- \------ \-------------- \-----
0 Time 284807 non\-null float64
1 V1 284807 non\-null float64
2 V2 284807 non\-null float64
3 V3 284807 non\-null float64
4 V4 284807 non\-null float64
5 V5 284807 non\-null float64
6 V6 284807 non\-null float64
7 V7 284807 non\-null float64
8 V8 284807 non\-null float64
9 V9 284807 non\-null float64
10 V10 284807 non\-null float64
11 V11 284807 non\-null float64
12 V12 284807 non\-null float64
13 V13 284807 non\-null float64
14 V14 284807 non\-null float64
15 V15 284807 non\-null float64
16 V16 284807 non\-null float64
17 V17 284807 non\-null float64
18 V18 284807 non\-null float64
19 V19 284807 non\-null float64
20 V20 284807 non\-null float64
21 V21 284807 non\-null float64
22 V22 284807 non\-null float64
23 V23 284807 non\-null float64
24 V24 284807 non\-null float64
25 V25 284807 non\-null float64
26 V26 284807 non\-null float64
27 V27 284807 non\-null float64
28 V28 284807 non\-null float64
29 Amount 284807 non\-null float64
30 Class 284807 non\-null int64
dtypes: float64\(30\), int64\(1\)
memory usage: 67.4 MB查看分类类别:
f,ax\=plt.subplots\(1,2,figsize\=\(18,8\)\)
df\['Class'\].value\_counts\(\).plot.pie\(explode\=\[0,0.1\],autopct\='\%1.1f\%\%',ax\=ax\[0\],shadow\=True\)
ax\[0\].set\_title\('dağılım'\)
ax\[0\].set\_ylabel\(''\)
sns.countplot\('Class',data\=df,ax\=ax\[1\]\)
ax\[1\].set\_title\('Class'\)
plt.show\(\)
rob\_scaler \= RobustScaler\(\)
df\['Amount'\] \= rob\_scaler.fit\_transform\(df\['Amount'\].values.reshape\(\-1,1\)\)
df\['Time'\] \= rob\_scaler.fit\_transform\(df\['Time'\].values.reshape\(\-1,1\)\)
df.head\(\)
创建基类模型:
X \= df.drop\("Class", axis\=1\)
y \= df\["Class"\]
X\_train, X\_test, y\_train, y\_test \= train\_test\_split\(X, y, test\_size\=0.20, random\_state\=123456\)
model \= LogisticRegression\(random\_state\=123456\)
model.fit\(X\_train, y\_train\)
y\_pred \= model.predict\(X\_test\)
accuracy \= accuracy\_score\(y\_test, y\_pred\)
print\("Accuracy: \%.3f"\%\(accuracy\)\)我们创建的模型的准确率评分为0.999。我们可以说我们的模型很完美吗?混淆矩阵是一个用来描述分类模型的真实值在测试数据上的性能的表。它包含4种不同的估计值和实际值的组合。

def plot\_confusion\_matrix\(cm, classes,
title\='Confusion matrix',
cmap\=plt.cm.Blues\):
plt.rcParams.update\(\{'font.size': 19\}\)
plt.imshow\(cm, interpolation\='nearest', cmap\=cmap\)
plt.title\(title,fontdict\=\{'size':'16'\}\)
plt.colorbar\(\)
tick\_marks \= np.arange\(len\(classes\)\)
plt.xticks\(tick\_marks, classes, rotation\=45,fontsize\=12,color\="blue"\)
plt.yticks\(tick\_marks, classes,fontsize\=12,color\="blue"\)
rc\('font', weight\='bold'\)
fmt \= '.1f'
thresh \= cm.max\(\)
for i, j in itertools.product\(range\(cm.shape\[0\]\), range\(cm.shape\[1\]\)\):
plt.text\(j, i, format\(cm\[i, j\], fmt\),
horizontalalignment\="center",
color\="red"\)
plt.ylabel\('True label',fontdict\=\{'size':'16'\}\)
plt.xlabel\('Predicted label',fontdict\=\{'size':'16'\}\)
plt.tight\_layout\(\)
plot\_confusion\_matrix\(confusion\_matrix\(y\_test, y\_pred\=y\_pred\), classes\=\['Non Fraud','Fraud'\],
title\='Confusion matrix'\)
非欺诈类共进行了56875次预测,其中56870次(TP)正确,5次(FP)错误。
非欺诈类共进行了56875次预测,其中56870次(TP)正确,5次(FP)错误。
欺诈类共进行了87次预测,其中31次(FN)错误,56次(TN)正确。
该模型可以预测欺诈状态,准确率为0.99。但当检查混淆矩阵时,欺诈类的错误预测率相当高。也就是说该模型正确地预测了非欺诈类的概率为0.99。但是非欺诈类的观测值的数量高于欺诈类的观测值的数量,这拉搞了我们对准确率的计算,并且我们更加关注的是欺诈类的准确率,所以我们需要一个指标来衡量它的性能。
选择正确的指标
在处理不平衡数据集时,选择正确的指标来评估模型的性能非常重要。传统指标,如准确性、精确度和召回率,可能不适用于不平衡的数据集,因为它们没有考虑数据中类别的分布。
经常用于不平衡数据集的一个指标是 F1 分数。F1 分数是精确率和召回率的调和平均值,它提供了两个指标之间的平衡。计算如下:
F1 = 2 * (precision * recall) / (precision + recall)
另一个经常用于不平衡数据集的指标是 AUC-ROC。AUC-ROC 衡量模型区分正类和负类的能力。它是通过绘制不同分类阈值下的TPR与FPR来计算的。AUC-ROC 值的范围从 0.5(随机猜测)到 1.0(完美分类)。
print\(classification\_report\(y\_test, y\_pred\)\)
precision recall f1\-score support
0 1.00 1.00 1.00 56875
1 0.92 0.64 0.76 87
accuracy 1.00 56962
macro avg 0.96 0.82 0.88 56962
weighted avg 1.00 1.00 1.00 56962返回对0(非欺诈)类的预测有多少是正确的。查看混淆矩阵,56870 + 31 = 56901个非欺诈类预测,其中56870个预测正确。0类的精度值接近1 (56870 / 56901)
返回对1 (欺诈)类的预测有多少是正确的。查看混淆矩阵,5 + 56 = 61个欺诈类别预测,其中56个被正确估计。0类的精度为0.92 (56 / 61),可以看到差别还是很大的
过采样
通过复制少数类样本来稳定数据集。
随机过采样:通过添加从少数群体中随机选择的样本来平衡数据集。如果数据集很小,可以使用这种技术。可能会导致过拟合。randomoverampler方法接受sampling_strategy参数,当sampling_strategy = ' minority '被调用时,它会增加minority类的数量,使其与majority类的数量相等。
我们可以在这个参数中输入一个浮点值。例如,假设我们的少数群体人数为1000人,多数群体人数为100人。如果我们说sampling_strategy = 0.5,少数类将被添加到500
y\_train.value\_counts\(\)
0 227440
1 405
Name: Class, dtype: int64
from imblearn.over\_sampling import RandomOverSampler
oversample \= RandomOverSampler\(sampling\_strategy\='minority'\)
X\_randomover, y\_randomover \= oversample.fit\_resample\(X\_train, y\_train\)采样后训练
model.fit\(X\_randomover, y\_randomover\)
y\_pred \= model.predict\(X\_test\)
plot\_confusion\_matrix\(confusion\_matrix\(y\_test, y\_pred\=y\_pred\), classes\=\['Non Fraud','Fraud'\],
title\='Confusion matrix'\)
应用随机过采样后,训练模型的精度值为0.97,出现了下降。但是从混淆矩阵来看,模型的欺诈类的正确估计率有所提高。
SMOTE 过采样:从少数群体中随机选取一个样本。然后,为这个样本找到k个最近的邻居。从k个最近的邻居中随机选取一个,将其与从少数类中随机选取的样本组合在特征空间中形成线段,形成合成样本。
from imblearn.over\_sampling import SMOTE
oversample = SMOTE\(\)
X\_smote, y\_smote = oversample.fit\_resample\(X\_train, y\_train\)使用SMOTE后的数据训练
model.fit\(X\_smote, y\_smote\)
y\_pred = model.predict\(X\_test\)
accuracy = accuracy\_score\(y\_test, y\_pred\)
plot\_confusion\_matrix\(confusion\_matrix\(y\_test, y\_pred=y\_pred\), classes=\['Non Fraud','Fraud'\],
title='Confusion matrix'\)
可以看到与基线模型相比,欺诈的准确率有所提高,但是比随机过采样有所下降,这可能是数据集的原因,因为SMOTE采样会生成心的数据,所以并不适合所有的数据集。
总结
在这篇文章中,我们讨论了处理不平衡数据集和提高机器学习模型性能的各种技巧和策略。不平衡的数据集可能是机器学习中的一个常见问题,并可能导致在预测少数类时表现不佳。
本文介绍了一些可用于平衡数据集的重采样技术,如欠采样、过采样和SMOTE。还讨论了成本敏感学习和使用适当的性能指标,如AUC-ROC,这可以提供更好的模型性能指示。
处理不平衡的数据集是具有挑战性的,但通过遵循本文讨论的技巧和策略,可以建立有效的模型准确预测少数群体。重要的是要记住最佳方法将取决于特定的数据集和问题,为了获得最佳结果,可能需要结合各种技术。因此,试验不同的技术并使用适当的指标评估它们的性能是很重要的。
#激流检测和定位的可解释深度学习
离岸流是一种强大的局部水流,沿着海岸移动并远离海岸。最近的研究表明,离岸流造成的溺水仍然是海滩安全的主要威胁。在决定指定巡逻区域的位置时,识别离岸流对于救生员来说很重要。当救生员不在巡逻时,公众在决定去哪里游泳时也需要信息。
在这里,新西兰国立水与大气研究所 (NIWA)的研究人员提出了一种人工智能 (AI) 算法,该算法既可以识别图像/视频中是否存在裂流,也可以定位裂流发生的位置。
虽然 AI 在裂流电流检测和定位方面取得了一些重大进展,但缺乏研究确保 AI 算法可以很好地推广到各种沿海环境和海洋条件。该研究使用了一种可解释的 AI 方法,即梯度加权类激活图 (Grad-CAM),这是一种用于非晶裂口电流检测的新方法。训练数据/图像多种多样,包含各种环境设置中的裂流,确保模型泛化。一个开放获取的离岸流空中目录被用于模型训练。
在这里,还通过应用各种随机图像变换(例如,透视、旋转变换和加性噪声)来增强航拍图像,这通过泛化显著提高了模型性能。为了考虑到不同的环境设置,一个包含雾、阴影和雨的综合生成的训练集也被添加到 rip 电流图像中,从而将训练数据集增加了大约 10 倍。可解释的 AI 显著提高了无界裂流检测的准确性,当对来自倾斜角度的冲浪相机的独立视频进行验证时,它可以在大约 89% 的时间内正确分类和定位裂流。新颖性还在于无需预定义边界框即可捕获非晶裂口电流结构的某些形状特征的能力,因此可以使用无人机等远程技术。
该研究以「Interpretable Deep Learning Applied to Rip Current Detection and Localization」为题,于 2022 年 11 月 18 日发布在《Remote Sensing》。
激流被定义为沿岸和远离海岸移动并穿过破碎带的强大的局部水流。由于质量和动量守恒,裂口电流形成。破浪将地表水推向海岸线。由于重力的作用,这些多余的水到达海岸线并流回开阔水域。水通过阻力最小的路线移动,因此,通常会在优先位置形成离岸流。这些包括沙洲中的局部起伏或断裂或没有或较低碎波的区域。离岸流的形成并不局限于海洋,当有足够的波浪能量时,也可以在大型湖泊中形成。有多种因素可以优先发展离岸流。这些包括海滩形态、波高、风向和潮汐。因此,一些海岸线比其他海岸线更容易受到离岸流的影响。由于预测形态的复杂性,大量研究采用概率预测方法。
据报道,离岸流对世界各地的海滩游客来说是最危险的安全风险,在澳大利亚,离岸流造成的死亡人数超过洪水、飓风和龙卷风的总和。根据季节和地点的不同,海滩给海滩游客带来了不同程度的风险。例如,大浪、强风和显着潮汐变化的裸露海滩通常会带来更大的风险。重要的研究工作也已投入到与离岸电流相关的危害的交流中。有研究强调了救生员在海滩上的重要性,也强调了直接调查和采访当前幸存者以获得对事件的人类行为方面的宝贵见解的重要性。
虽然裂流是一种众所周知的海洋现象,但许多海滩游客不知道如何可靠地识别和定位裂流。这也适用于救生员,由于他们通常从高度倾斜的角度观察海洋,他们同样可能难以识别某些离岸流,尤其是当海岸形态复杂或海洋气象条件迅速变化时。尽管有警告标志和教育活动,这个沿海过程仍然对海滩安全构成严重威胁,一些国家报告死亡人数增加。因此,用于有效识别和预测这一动态过程的新技术的研究和开发正在进行中。这些技术,旨在将海滩游客的安全从被动转变为预防,并且需要有效和明确的警告/通知传播。目的是准确预测和/或识别激流,以告知公众发生激流的位置,以便他们做出最安全的游泳地点的明智决定。
受欢迎的海滩通常有救生员巡逻,一些海滩还配备了摄像头。这些摄像机的功能可以用于安全、提供实时天气和海滩状况信息,或者在某些情况下用于监控沿海过程。30多年来,海岸图像一直被用于检测海浪特征、海滩和近岸形态,美国、英国、荷兰和澳大利亚以及新西兰的卡姆时代(Cam Era)等综合和半自动化系统已经开发完成。其他系统包括 HORUS、CoastalCOMS、KOSTASYSTEM、COSMOS、SIRENA、Beachkeeper 和 ULISES。
用于闪存撕裂警告的 Lifeguarding Operational Camera Kiosk System (LOCKS) 是另一个例子。虽然许多海滩使用单个或多个摄像头网络,但很少(如果有的话)海滩具有实时处理功能来识别裂缝等特征。因此,大多数离岸电流检测都是由救生员和海滩游客手动完成的。因此,任何激流预报或实时识别工具都可以帮助救生员和海滩游客进行与激流相关的救援和溺水。
虽然声学多普勒电流剖面仪 (ADCP)、浮动漂移器和染料等原位测量已用于研究和量化裂口电流,但这些既费时又昂贵,并且必须在发生裂口的地方使用。与图像处理技术相比,这使得它们在识别裂口方面用处不大,图像处理技术可以以低成本和低工作量观察大面积区域。
使用 AI 和其他图像和信号处理技术来分类和定位离岸电流也得到了显著的应用,例如,波浪破碎和海岸形态。图像和其他信号处理技术通常使用时间曝光图像,或简单地通过对一系列帧进行平均。该技术适用于存在波浪不突破裂口电流位置并因此在视觉上更暗的裂口电流。在这里,具有一致碎波的地方会呈现模糊的白色,而裂口的位置会显得更暗。
这些技术有几个限制。首先,由于对至少 10 分钟的时间进行平均,它无法检测和捕获非平稳的、快速变化的离岸电流,而这在冲浪救生的背景下是必需的。其次,自动推导离岸流的阈值存在重大挑战,离岸流的阈值随基础测深的变化而变化。此外,通过这种方法检测裂口电流没有一个万能的阈值(也由于环境光条件)。捕获单个图像帧之间运动的光流方法是另一种有前途的技术。该技术克服了通过时间平均检测快速变化的裂口电流的问题。然而,要使这种方法自动化也具有挑战性,因为该算法需要量化波浪作用、可能的离岸流和背景运动之间的差异。最近的研究表明,这些方法对海滩测深很敏感,因此裂流电流检测的阈值因位置而异。
这些方法常常导致许多误报。另外,由于计算限制,这些技术难以实时部署。然而,有团队确实提出了最近的研究,该研究利用固定的摄像机角度在冲浪区利用二维波平均电流(光流)。后来也有进一步发展,并且两项研究都可以捕获非晶裂口电流结构。还有团队使用图像增强策略来识别不同的海滩状态,其中 rip 通道的存在与特定类的存在相关联。
因此,启用更多与海滩相关的相关信息对于物理过程识别很有用。许多传统图像处理技术的解决方案是深度学习技术,例如卷积神经网络 (CNN)。虽然深度学习模型的训练速度可能相对较慢,但它们在实时环境中的部署和应用速度很快,这对于无人机技术和当前研究的部分设想未来计划也很有前景。

在最新的研究中,新西兰国立水与大气研究所 (NIWA)的研究人员研究了可解释人工智能的有用性,特别是在模型改进的背景下。研究人与通过 CNN 等深度学习技术进行监督学习的一些优势,以及它们从经验中学习和学习复杂的依赖关系和特征以导出一组模型权重/参数以产生最大准确度的能力。CNN 还需要较少的人工输入,这优于需要定义阈值的传统图像处理技术。

由于 CNN 等许多 AI 算法具有许多可调参数,因此它们需要大量的训练数据。训练数据缺乏多样性也会导致模型泛化能力差,并且在裂流检测的背景下,模型需要来自代表各种不同环境设置的海滩的训练数据。虽然训练 CNN 所需的数据量可能非常大(实际上可能无法获得),但有许多方法可以克服这一点并减少过度拟合。例如,数据增强通过一系列平移(例如旋转和透视变换)来操纵每个单独的图像,从而增加了训练数据量。此外,迁移学习已成为一种广泛使用的技术,用于在小型数据集上训练基于 AI 的模型,其中基于 AI 的模型首先在非常大的数据集上进行训练,然后在较小的数据集上进行微调。
典型的 AI 研究问题侧重于检测具有明确边界的对象(例如,人、狗、汽车等)。要训练基于 AI 的模型以对每个图像中对象的位置进行分类和定位,需要在每个对象周围定义一个边界框。
一些研究已经成功地使用对象分类算法来定位和预测裂流的发生。有其他团队使用 CNN 预测裂流的发生,也有团队使用更快的 R-CNN(基于区域的 CNN)来定位(预测边界框)和预测裂流的发生 ,实现了超过 98% 的测试数据集的准确性。裂流检测的另一个挑战是它们不一定在每个视频帧中观察到,而是可以在一系列图像上观察到裂流。由于视频序列的训练既耗时又需要更多的训练数据(例如,独特的视频),现有方法已经在裂流的静态图像上使用了 CNN。为了避免未观察到裂口电流的情况,研究人与使用了一种帧聚合技术,其中预测在一个时间间隔内聚合。他们指出,当预测在一段时间内汇总时,假阳性/阴性率会降低。
虽然这些方法在裂口电流检测和定位方面取得了早期成功,但在现实环境中实施基于 AI 的算法存在几个问题,该研究旨在解决这些问题:
(1)没有考虑对裂口电流的非晶结构进行分类,
(2)人工智能模型的可解释性,以了解模型是否正在学习离岸流的正确特征以及模型中是否存在缺陷,
(3)增强 AI 模型泛化能力的替代数据增强方法,
(4)建立对基于 AI 的模型预测的信任。
新方法的一个主要优点是它们不依赖于边界框。这些通常是预定义的,因此只能从其中包含的信息中学习。在这里,该模型可以捕获无定形结构(裂流形状)的一些特征,因为它学习了各种没有边界框的可能的海岸特征。这使得这项技术能够与无人机一起使用(沿轨道改变摄像机视图),而不仅仅是固定角度摄像机。

新方法引入了一种可解释的 AI 方法,即梯度加权类激活图 (Grad-CAM),以解释经过训练的基于 AI 的模型的预测。Grad-CAM 能够揭示典型的黑盒 AI,并使模型能够了解输入图像中的哪些区域/像素影响了基于 AI 的模型的预测。反过来,这也使得能够预测分类裂口电流的非晶边界。目前的方法并不像 Faster R-CNN 那样限制 AI 模型学习特定于放置的边界框的特征,并且你只看一次 (YOLO) 对象检测方法,其中算法被迫学习非常具体的监督特征, 而可能还有其他相关的特征。新方法还在识别独立于传统准确性指标的主观模型缺陷的背景下引入了可解释的 AI。这些方法可以帮助提供更好的模型开发和增强策略,以改进基于 AI 的模型的泛化。基于人工智能的复杂模型的决策无法被很好地理解,因此很难被信任,尤其是在涉及安全和人类健康的冲浪救生环境中。因此,对于真实世界的应用,显然需要可靠、灵活(无边界框)和高性能的基于 AI 的撕裂检测模型。
#时间向量 (time vectors)
语言模型究竟是如何感知时间的?如何利用语言模型对时间的感知来更好地控制输出甚至了解我们的大脑?最近,来自华盛顿大学和艾伦人工智能研究所的一项研究提供了一些见解。他们的实验结果表明,时间变化在一定程度上被编码在微调模型的权重空间中,并且权重插值可以帮助自定义语言模型以适应新的时间段。
具体来说,这篇论文提出了时间向量(time vectors)的概念,这是一种让语言模型适应新时间段的简单方法。论文发布后立即引起了一些研究者的注意。新加坡海事智能公司 Greywing 联合创始人、CTO Hrishi Olickel 称赞这篇论文是他今年读过最好的论文之一。
他将本文的核心步骤概括为:
- 获取 Twitter 和新闻数据,并按年份和月份进行分类;
- 选择一个 LLM,并按月或按年对其副本分别进行微调,更新模型权重;
- 从原始 LLM 的权重中分别减去微调后模型的权重,得到「时间向量」。
权重差值此时可以作为一种向量,用于探索模型在这段时间内学到了什么。那么具体来说能用这个向量做些什么呢?

首先,可以检查微调是否有效 —— 从结果来说微调确实有效。模型困惑度和 F1 值强烈表明,当输入的数据符合微调后的时间时,任务性能有相应的提高!
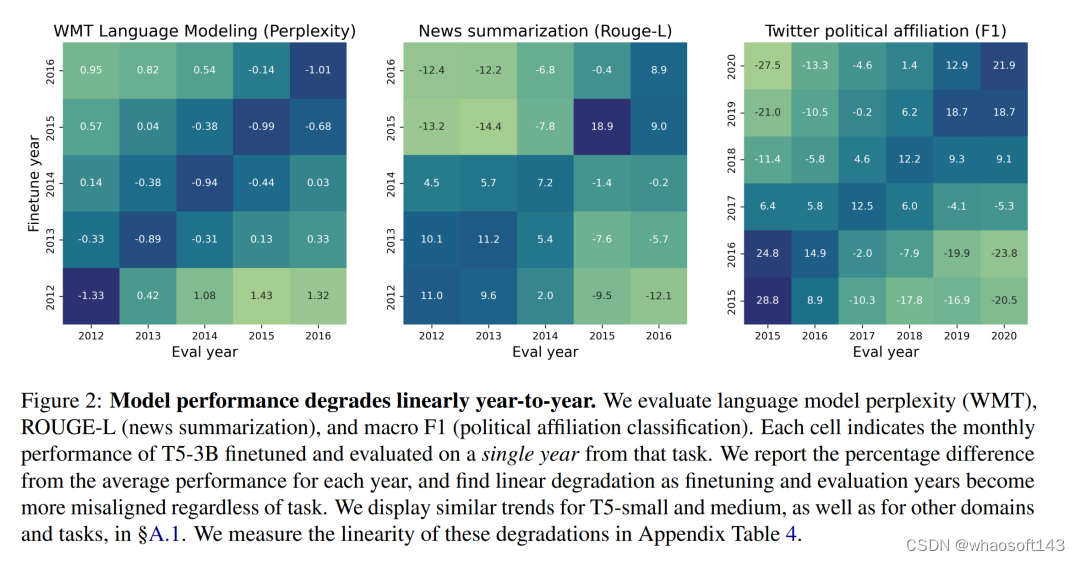
同样有趣的是,随着训练数据时间的推移,模型的性能呈线性下降。这一点在月份粒度和年份粒度上的结果都是如此。同时在特定月份训练的模型在同年其他某几个月份的表现也会相对较好(如下图中的对角线条纹现象)。

Hrishi Olickel 猜想这是由于语义上存在的相似性(相同的月份名称),不是因为模型产生了深层次的理解。并且如果能研究一下不同模型对应层之间的差值有多大,也许就能知道这种影响有多深。同样有趣的是向量的组织方式。

Hrishi Olickel 认为能够提出一个存在内部时间的模型,是相当惊人的。人类到现在都不知道时间是如何在大脑中工作的,但如果我们是语言驱动的学习者(如 LLM),而「意识」是一个内心里循环启动的「进程」,那么人和 LLM 可能会有相似之处。
更有趣的地方在于,有了这些向量之后,就可以在它们之间进行插值,从而在没有进行微调的年份也获得较好的性能!向量之间的插值是简单的算术运算 —— 系数加法。
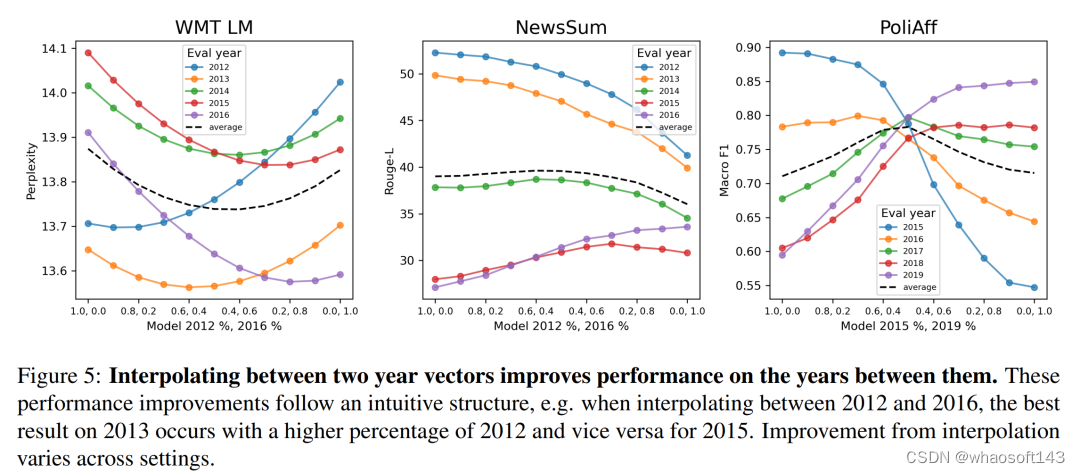

与之前的基于任务进行训练得到的模型权重向量一样,这种插值方法可能是在找出真正的迁移学习之前,可行的训练方法之一。如果能从微调中进行插值,就能对模型输出进行精细且低成本的控制,省去微调的成本和时间。
基于此,Hrishi Olickel 提出了几个猜想:
- 这项工作是在标准预训练模型(三种规模的 T5)上完成的。如果在开始训练模型时设置一些约束条件,强制对隐空间中的概念和时间进行更好的聚类,那么这种方法很可能会带来更强的结果。
- 另一个可能会有趣的探索是通过观察模型的激活情况来了解对应的时间段。
- 论文中依靠模型从 prompt 中「找出」时间和概念,并激活正确的部分。如果加入一些模块也许会有意想不到的效果,比如类似于 MoE 风格的路由。路由经过训练后,可以在同一模型的不同微调版本之间进行 token-to-token 的转换。

Hrishi Olickel 认为这个章节非常有趣。从这段文字中不能确定他们的意思是否是交换权重时只交换插值,如果是并且能奏效,那就太棒了。
Hrishi Olickel 表示,对人工智能(至少是基于语言模型的人工智能)的新理解来自于我们能够实时编辑和利用这些模型权重的能力 —— 他强烈怀疑(或希望)其中一些能力将帮助我们理解人类的大脑。
以下是论文的具体内容。
论文概览
时间变化是语言的一个基本特征。正如本文第 3 章中所提到的,时间变化在语言模型开发中表现为时间错位(temporal misalignment),即训练数据和测试数据的时间偏差会导致模型在时间段不同的情况下性能大幅下降。这就需要采用适应技术,根据需要定制特定时间段的模型。然而,由于时间尺度众多,而且可能无法获得目标时间段的数据,因此设计此类技术十分困难。
最近的研究表明,神经网络的行为可以通过微调模型参数之间的闭式插值进行编辑。本文证明了权重空间的插值也可用于低成本地编辑语言模型,创造模型在不同时期的行为。
在第 4 章中,本文引入了时间向量,作为任务向量的扩展(参见论文「Editing Models with Task Arithmetic」)。即在单个时间段的文本上对预训练的语言模型进行微调后,减去原预训练模型的权重,得到一个新向量。这个向量代表了权重空间的移动方向,可以提高模型在处理目标时间段文本时的性能。
在第 2 章中,本文利用按时间组织的数据集分析时间向量的结构,用于语言建模、分类和总结。研究结果一致表明,时间向量直观地分布在一个流形上;在时间上更接近的年份或月份产生的时间向量在权重空间上也更接近。同样,在 4.2 节中,本文还表明,年度和月度中的时间退化问题与时间向量之间的角度密切相关。
本文利用这种时间向量结构来引导模型,使其更好地覆盖新的时间段的数据。通过在两个时间向量之间进行插值,可以产生新的向量,这些向量应用到预训练模型时,可以提高模型在间隔月份或年份中的性能(第 4.3 节)。该结构还可用于跨时间段泛化特定任务模型,并使用专门用于未标记数据的类似时间向量(第 4.4 节)。
本文的研究结果表明,微调模型的权重空间在一定程度上对时间变化进行了编码,权重插值可以帮助定制语言模型以适应新的时间段。本文作者开源了论文的代码、数据和超过 500 个根据特定时间段微调的模型。
多时间尺度上的时间错位
以年为单位的模型线性性能退化
之前关于时间错位的研究表明,模型会随着时间逐年退化。
为了证实这些结果,本文在每个数据集的每个年度分段上对 T5-small、T5-large 和 T5-3b 进行了微调。然后,在测试数据的每个其他时间分段上对这些经过调整的模型进行评估。
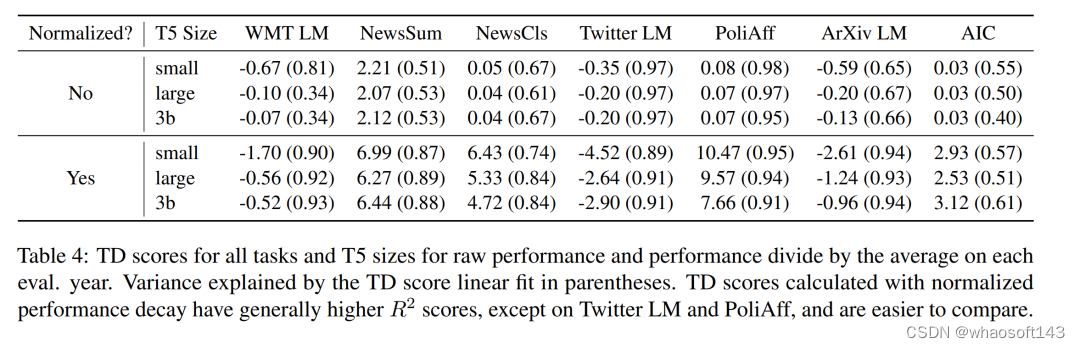
图 2 中以年为单位展示了时间错位热图,以及与年平均值相比的困惑度变化百分比(避免固有的年度性能差异)。与之前的研究结果一致,本文观察到每个任务中都存在着线性退化的特点,无论模型的大小(更多详情请参见表 4)。与 早先研究结果一样,有些任务(如政治派别分类)的退化比其他任务更明显。原文附录中的 §A.2 中会对这些差异进行量化。
以月为单位的模型非线性性能退化
接下来,本文介绍了按月为单位的时间错位问题。这个问题尚未得到探讨。论文作者在 2012-2016 年间的 WMT 数据集上,按月份分段,并训练了 T5-small,从而得到了 58 个经过月份分类的模型。然后,在这些按月拆分的多个模型上,总共进行了 3,364 次验证实验。
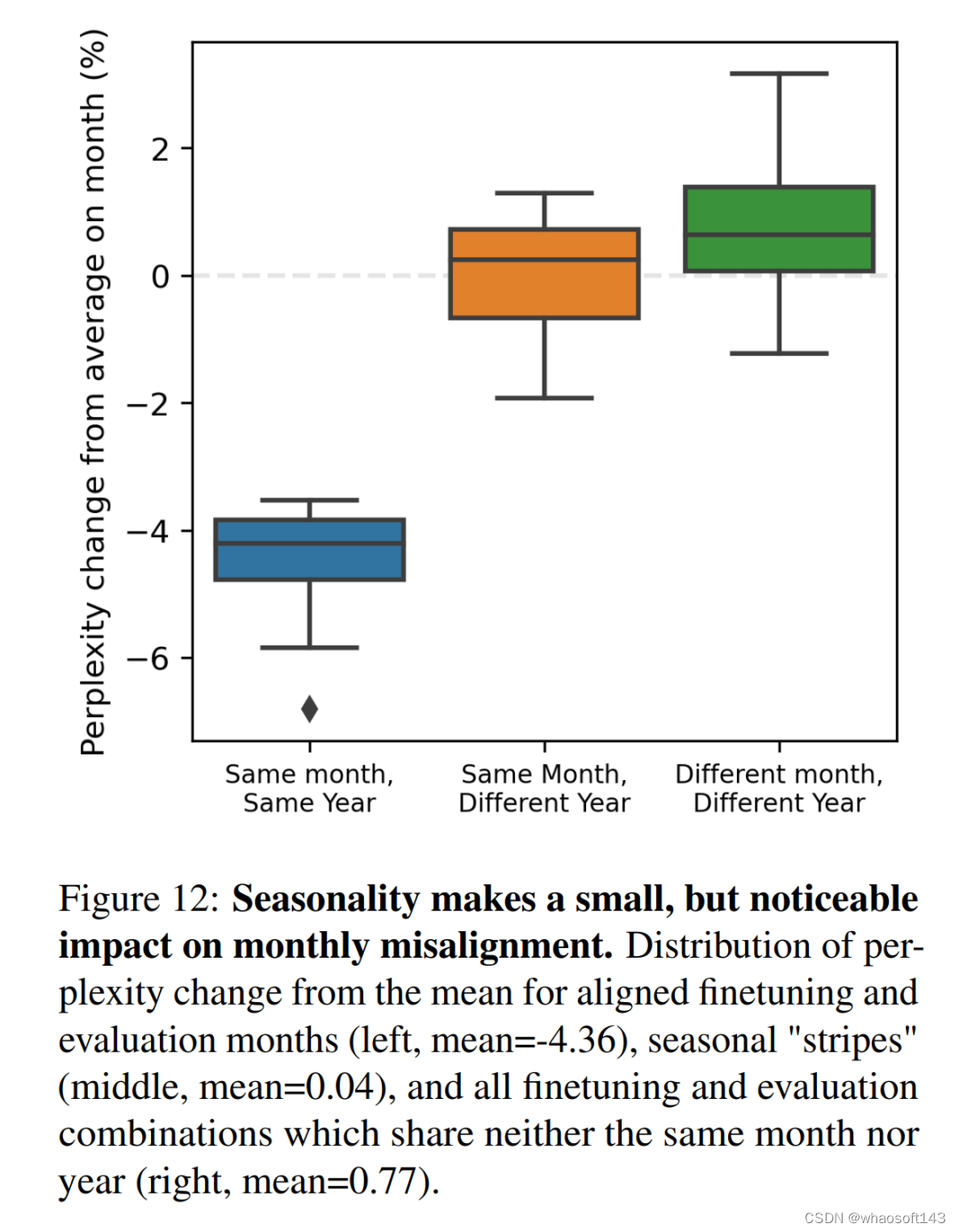
如图 3 所示,在 WMT 数据集的特定月份上对模型进行微调和评估,可以发现时间错位的非线性模式,与每年的月份周期相对应。每隔 12 个月出现的平行于对角线的条纹可以捕捉到这种模式,这表明特定月份的模型在其他年份的相同月份往往表现更好。本文在附录图 12 中量化了这些困惑度差异。还在 §A.4 中总结了线上训练设置中的模型退化模式。
基于时间向量的时间自适应
时间向量相似度与时间退化的相关性
本文在图 4 中用 UMAP 对时间向量进行了可视化,这表明在权重空间中更接近的时间向量在时间上也更接近。为了验证这一假设,本文测量了在不同时间段训练的每对时间向量的模型权重之间的余弦相似度(见附录第 A.1 节)。
本文的结果显示,这一相似度指标和性能(图 11)随着时间的推移,存在相似的衰减。
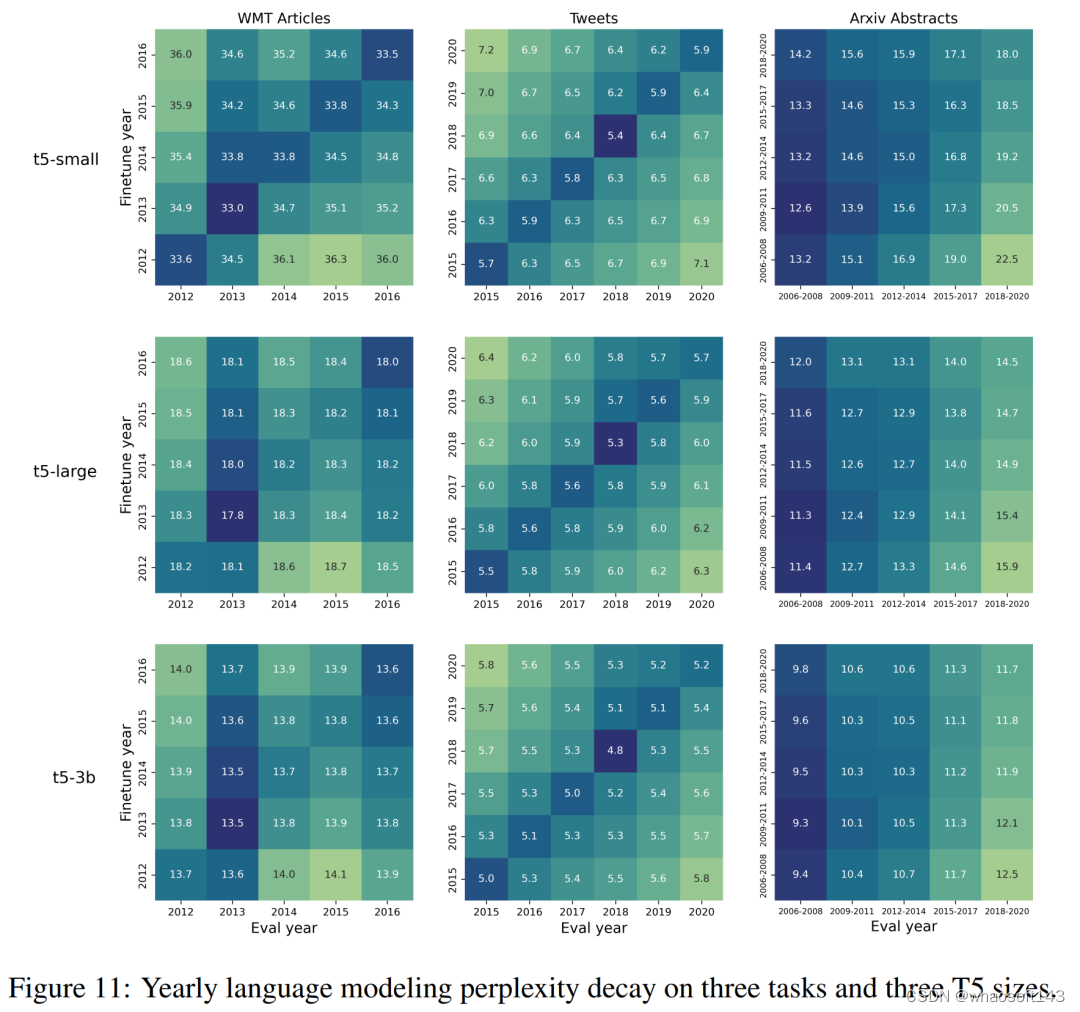
表 1 显示,余弦相似度与不同年份相对性能变化之间的相关性在 WMT 语言建模中最高。同时,这种相关性在不同规模的 T5 中也基本相似,在 WMT LM 中,T5-small 的得分高于 T5-large 和 T5-3b,且绝对值均不低于 0.6。
这种关系也延伸到按月划分的尺度下。在两两月度之间, WMT 时间向量的余弦相似度中可以看到周期性条纹(见附图 9)。与平均值(图 3)和余弦相似性矩阵(图 9)相比,月度性能下降呈负相关(Pearson r = -0.667; p < 10-16)。附录 A.5 中分析了整个在线训练过程中单年时间向量的余弦相似性。
这些结果表明,时间向量的组织方式可以预测其在相应时间段的表现。接下来将探讨如何利用这种结构,通过时间向量之间的插值来提高新时间段的性能。
对中间时间进行插值
存档问题或采样率低会导致数据集在最新和最旧示例之间出现间隙。在没有数据的情况下,由于时间上的错位,预计模型在这些 "间隙" 时间上的表现会更差。在本节中,可以发现通过对最新和最旧时间的模型进行微调,可以更好地让模型适应这些时间段。
方法

结果
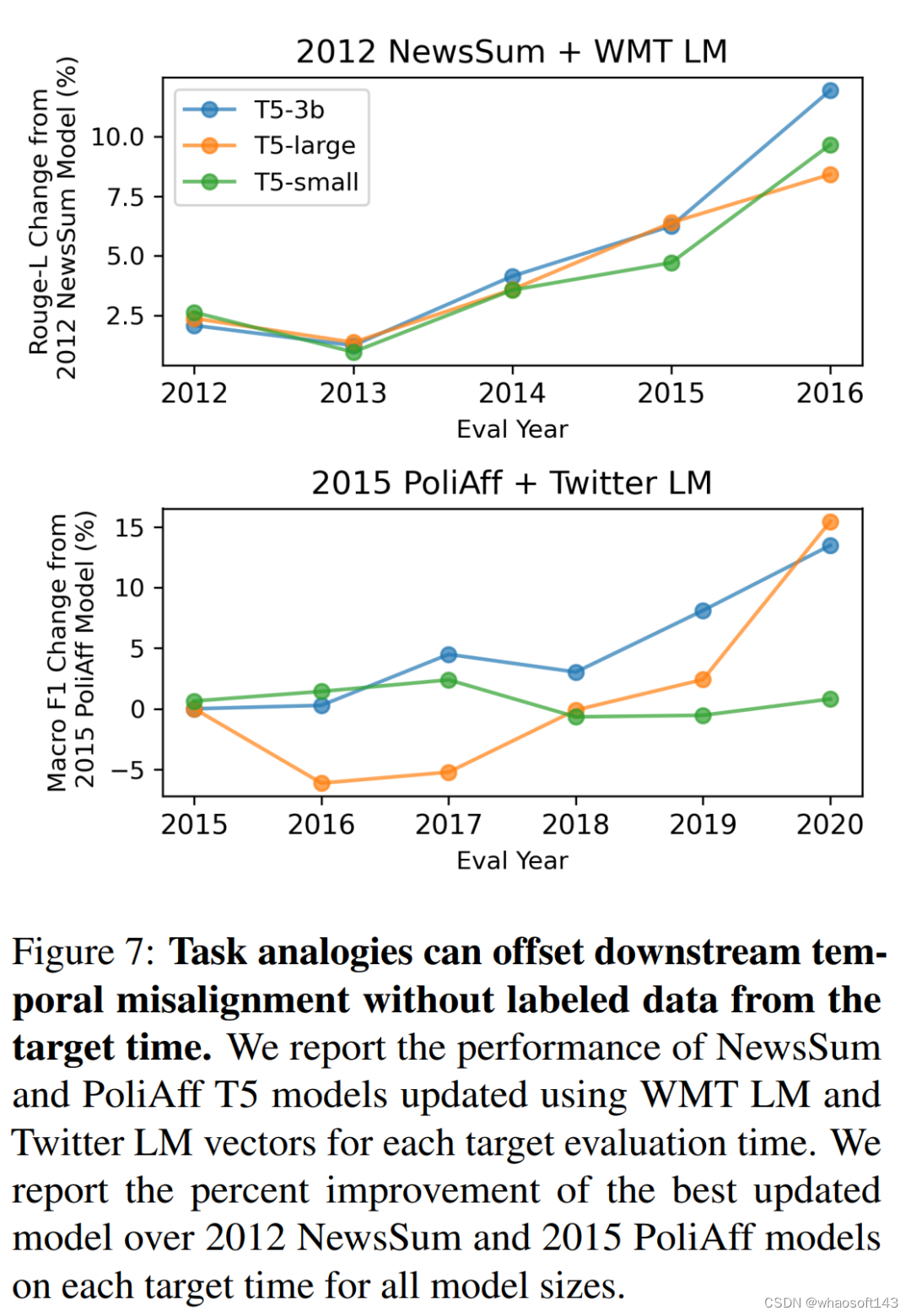
如图 5 所示,在 WMT LM 和 PoliAff 任务中,在起始年和结束年微调模型之间进行内插可以提高中间年份的性能。一般来说,中间年份(WMT LM 为 2014 年,PoliAff 为 2017 年)的改进幅度最大,而在更接近起始和结束时间的年份,改进幅度则会减小。不同设置下的改进模式也不尽相同,与 WMT LM 相比,PoliAff 在 α = 1.0 和 0.0 附近的性能变化更为平缓,而 NewsSum 在不同 α 之间的改进与验证年份之间的性能差异相比微乎其微。表 2 量化了这些变化,显示插值法缩小了时间对齐模型和错位模型之间的差距。PoliAff 的改进尤为显著,仅平均值就提高了近 8 个 macro-F1 百分点。
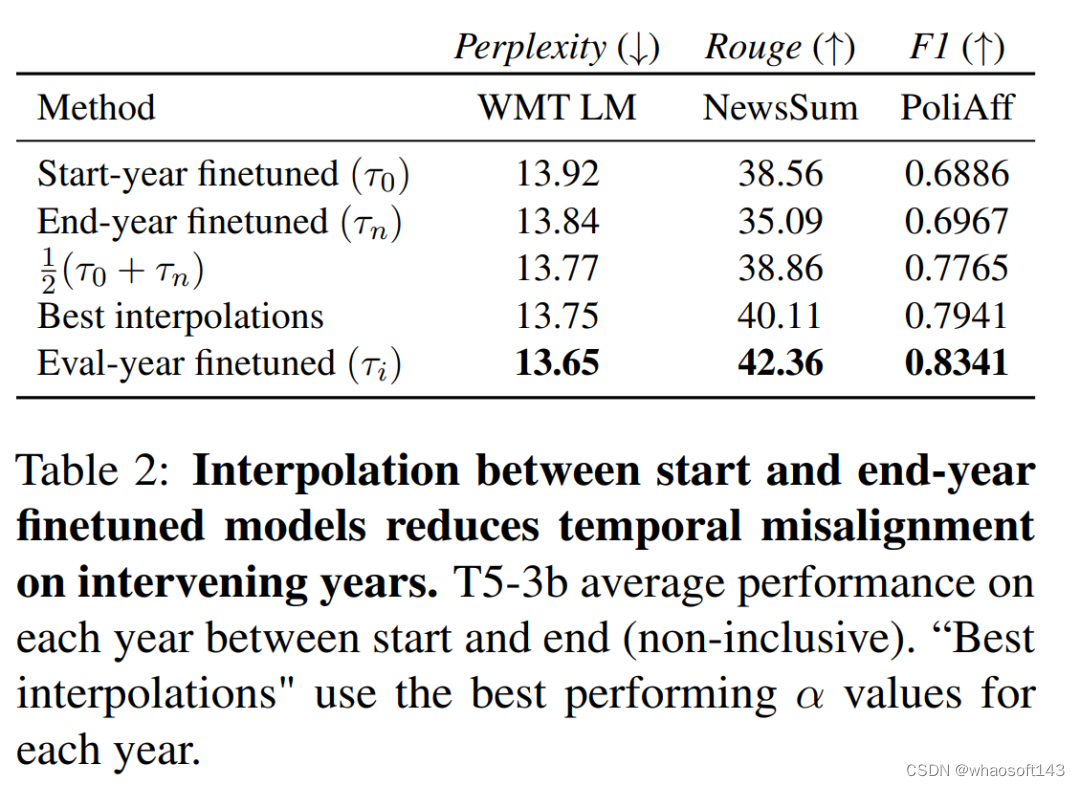
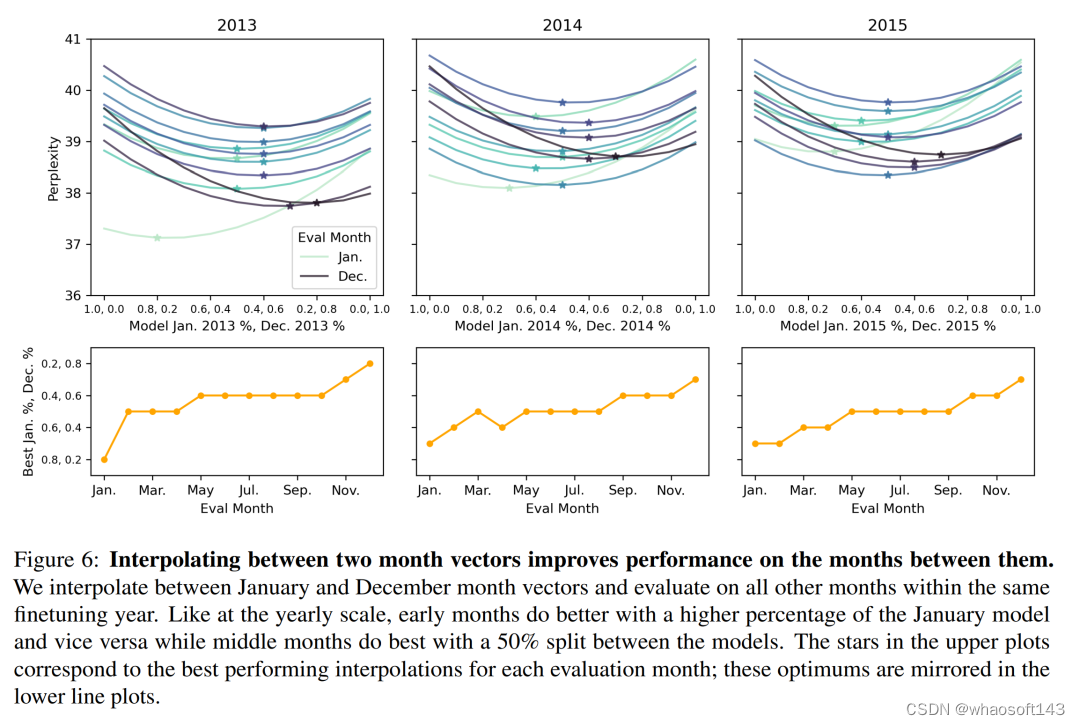
图 6 显示,这些结果扩展到按月划分的 WMT LM 后;可以在一年内 1 月和 12 月确定的时间向量之间进行插值,以提高这几个月的模型表现。每个月的最佳插值遵循一个直观的模式,1 月份模型的百分比越高,会导致前几个月的性能更好,反之亦然。
生成未来的时间模型
标注数据集创建于过去,因此,依赖监督进行微调的语言模型很快就会过时。更新这些模型的成本可能很高,需要进行额外的微调,还需要从更多最新的文本中创建标注数据集。本节将介绍一种新技术,使用任务类比算法,将在源时间段 j 上微调过的任务模型,更新至目标时间段 k,并且只包含 j 中未标记数据。 方法

本文在每个目标时间 t_k 上验证估计的 θ_k,遍历 α_1 ∈ [0.6, 0.8, . . 2.2]、α_2、α_3 ∈ [0.1, . . 0.6] 的所有组合,并报告与原始模型 θ_j 相比的最佳结果。本节使用 WMT LM 和 Twitter LM 时间向量,分别将 2012 年的 NewsSum 模型更新为 2013-2016 年,将 2015 年的 PoliAff 模型更新为 2016-2020 年。
结果
任务类比算法提高了 PoliAff 和 NewsSum 任务在未来年份的性能。图 7 显示,随着目标年份和起始年份的错位越来越大,与起始年份的微调相比,改进幅度也越来越大。模型大小也会影响性能,T5-large 和 T5-3b 的改进幅度更大。在 PoliAff 中,T5- small 与基线相比没有改善,而 T5-large 任务类比在 2016 和 2017 年的表现比基线差,在 2019 和 2020 年才有所改善。奇怪的是,作者发现只是缩放 α_1 也能提高模型完成未来几年任务的性能。附录 A.6 中报告了 α 消减和其他两个分类任务的结果。在这些任务中,研究者观察到的结果大多相似,但也有因任务而异的不一致之处。
#风格迁移~论文
1、StyleDiffusion: Controllable Disentangled Style Transfer via Diffusion Models
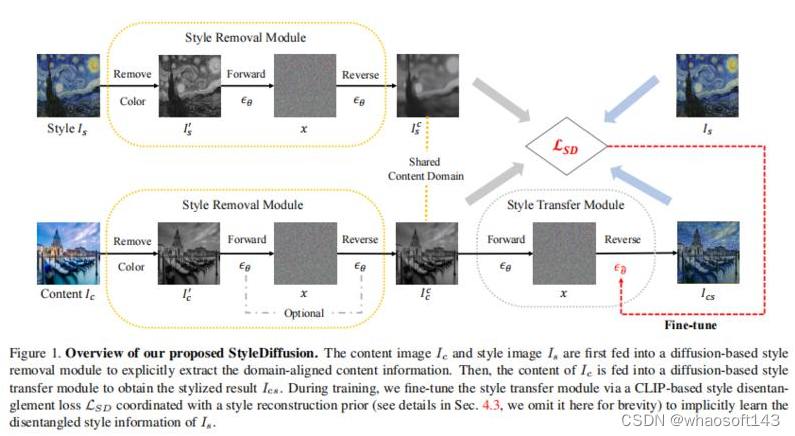
内容和风格(Content and style disentanglement,C-S)解耦是风格迁移的一个基本问题和关键挑战。基于显式定义(例如Gram矩阵)或隐式学习(例如GANs)的现有方法既不易解释也不易控制,导致表示交织在一起并且结果不尽如人意。
本文提出一种新的C-S解耦框架,不使用先前假设。关键是明确提取内容信息和隐式学习互补的风格信息,从而实现可解释和可控的C-S解耦和风格迁移。提出一种简单而有效的基于CLIP的风格解耦损失,其与风格重建先验一起协调解耦C-S在CLIP图像空间中。通过进一步利用扩散模型强大的风格去除和生成能力,实现了优于现有技术的结果,并实现了灵活的C-S解耦和权衡控制。
工作为风格迁移中的C-S解耦提供了新的见解,并展示了扩散模型在学习良好解耦的C-S特征方面的潜力。
2、Zero-Shot Contrastive Loss for Text-Guided Diffusion Image Style Transfer

扩散模型在文本引导的图像风格迁移中显示出巨大潜力,但由于其随机的性质,风格转换和内容保留之间存在权衡。现有方法需要通过耗时的扩散模型微调或额外的神经网络来解决这个问题。
为解决这个问题,提出一种零样本对比损失的扩散模型方法,该方法不需要额外的微调或辅助网络。通过利用预训练扩散模型中生成样本与原始图像嵌入之间的分块对比损失,方法可以以零样本的方式生成具有与源图像相同语义内容的图像。
方法不仅在图像风格迁移方面优于现有方法,而且在图像到图像的转换和操作方面也能保持内容并且不需要额外的训练。实验结果验证了方法有效性。https://github.com/YSerin/ZeCon
3、Diffusion in Style

基于这样一个关键观察:由Stable Diffusion生成的图像的风格与初始潜在张量相关联。如果不将这个初始潜在张量调整到风格,则微调会变得缓慢、昂贵且不切实际,特别是当只有少数目标样式图像可用时。相反,如果调整这个初始潜在张量,则微调会变得更加容易。
Diffusion in Style在样本效率和速度上具有数个数量级的提升。与现有方法相比,它还可以生成更加令人满意的图像,这一点在定性和定量比较中得到了证实。https://ivrl.github.io/diffusion-in-style/
4、PODIA-3D: Domain Adaptation of 3D Generative Model Across Large Domain Gap Using Pose-Preserved Text-to-Image Diffusion

最近,在3D生成模型方面取得重大进展,然而在多领域训练这些模型是一项具有挑战的工作,需要大量的训练数据和对姿势分布的了解。
文本引导的域自适应方法通过使用文本提示将生成器适应于目标域,避免收集大量数据。最近,DATID-3D在文本引导域中生成令人印象深刻的视图一致图像,利用文本到图像扩散模型保持文本的多样性。然而,将3D生成器调整到与源域存在显著领域差异的领域,仍具挑战,包括:1)转换中的形状和姿势权衡,2)姿势偏差,以及3)目标域中的实例偏差,导致生成的样本中3D形状差、文本图像对应性差和域内多样性低。
为解决这些问题,提出PODIA-3D流程,用保留姿势的文本到图像扩散式域适应的方法来进行3D生成模型训练。构建一个保留姿势的文本到图像扩散模型,在进行领域变化时使用极高级别的噪声。提出专用于一般的采样策略,以改善生成样本的细节。此外,为克服实例偏差,引入一种文本引导的去偏方法,以提高域内多样性。因此,方法生成出色的文本图像对应性和3D形状,而基线模型大多失败。定性结果和用户研究表明,方法在文本图像对应性、逼真程度、生成样本的多样性和3D形状的深度感方面优于现有的3D文本引导域自适应方法。https://gwang-kim.github.io/podia_3d/
5、DS-Fusion: Artistic Typography via Discriminated and Stylized Diffusion

介绍一种新方法,通过将一个或多个字体的字母进行风格化,视觉上传达输入单词语义,并确保输出保持可读性,自动生成艺术字体。
为应对一系列挑战,包括冲突的目标(艺术化风格化 vs. 可读性)、缺乏事实根据和庞大的搜索空间,方法利用大型语言模型将文本和视觉图像进行风格化,并基于扩散模型骨干构建一个无监督的生成模型。具体而言,采用潜在扩散模型(LDM)中的去噪生成器,并加入一个基于CNN的判别器,将输入风格调整到输入文本上。判别器使用给定字体的光栅化图像作为真实样本,将去噪生成器的输出作为伪样本。模型被称为DS-Fusion,表示具有有区分度和风格化的扩散。
大量示例、定性定量评估及消融研究展示方法质量和多样性。与CLIPDraw、DALL-E 2、Stable Diffusion以及由艺术家精心制作的字体进行的用户研究显示DS-Fusion的强大性能。https://ds-fusion.github.io/
#浅谈后向传递的计算量大约是前向传递的两倍
从前向传递、后向传递和优化器参数更新的浮点数计算次数入手,详解向传递的耗时为啥几乎是前向传递的两倍。
1. 前言
训练神经网络的一次迭代分为三步:(1)前向传递计算损失函数;(2)后向传递计算梯度;(3)优化器更新模型参数。在实验中,我们观察到一个现象:后向传递的耗时几乎是前向传递的两倍,相比之下,优化器更新的耗时几乎可以忽略。要解释这个现象,我们要从前向传递、后向传递和优化器参数更新的浮点数计算次数入手。

上图表示一次训练迭代中各个环节(前向传递、后向传递、通信环节、优化器更新)的耗时占比,来自于《PyTorch Distributed: Experiences on Accelerating Data Parallel Training》。上图中,纵轴表示耗时占比,FWD表示一次训练迭代中前向传递的耗时占比,BWD则表示一次训练迭代中后向传递的耗时占比,OPT表示一次训练迭代中优化器更新模型参数的耗时占比。从上图中可以看到,一次训练迭代中,后向传递的耗时几乎是前向传递的两倍,相比之下,优化器更新的耗时占比很小,几乎可以忽略。

上图表示GPipe流水线并行的调度策略,来自于《Efficient large-scale language model training on gpu clusters using megatron-lm》。上图中,横轴表示耗时,一个蓝色小块表示一个微批次的前向传递,一个绿色小块表示一个微批次的后向传递,黑色竖线表示一次流水线刷新,也就是优化器更新模型参数。从上图中可以看到,一个绿色小块的宽度大约是蓝色小块的二倍,一次训练迭代中,后向传递的耗时几乎是前向传递的两倍,相比之下,优化器更新的耗时占比很小,几乎可以忽略。
2. 反向传播算法是怎么工作的
反向传播算法已经是训练神经网络模型不可缺少的一部分。训练神经网络模型时,用梯度下降算法来学习和更新模型参数(包含权重weights和偏置bias),问题是如何计算损失函数关于模型参数的梯度呢?这就要用到反向传播(backpropagation)算法。
反向传播算法的核心是计算损失函数 关于神经网络权重 或偏置 的偏微分 或 ,这两个偏微分表达式就是梯度。梯度的物理意义是:我们改变网络权重和偏置可以在多大程度上影响损失函数 。
2.1 前向传递:计算神经网络的输出
在讨论反向传播算法之前,我们先以多层前馈神经网络为例,用基于矩阵的方法来计算神经网络的输出。在此过程中,先定义一些数学符号。
首先明确地定义神经网络中的权重参数,用 表示第 层第 个神经元到第 层第 个神经元的连接。例如,下图中的权重 表示第2层第4个神经元到第3层第2个神经元的连接。这个定义看起来有些麻烦,一个迷惑之处是 的顺序,应该用 表示输入神经元,用 表示输出神经元,而不是相反。但之后的计算中,你会看到这个定义是自然而然的。

类似地,我们定义网络中的偏置和激活。用 表示网络中第 层第 个神经元的偏置,用 表示网络中第 层第 个神经元的激活。下图给出了示例。

有了以上定义,我们就可以把网络第 层第 个神经元的激活 与第 层的激活联系起来。单个神经元的计算公式(逐点形式):
其中,求和是对第 层上所有神经元 的求和, 是激活函数。
为了以矩阵形式重写上式,我们为第 层定义一个权重矩阵 (weight matrix) ,表示连接到第 层的权重,矩阵第 行第 列的元素为 。设第 层的输入维度为 ,输出维度为 。则该权重矩阵 的形状为 。
同样地,我们定义一个偏置向量 (bias vector) ,它的元素是 ,形状是 。定义一个激活向量 (activation vector) ,它的元素是 ,形状是 。
重写上式需要的最后一个要素是向量化 (vectorization) 函数。核心是函数逐点应用到向量中的每个元素。
有了以上定义,我们就可以将上式改写为矩阵形式:
下标表示了矩阵或者向量的形状。这个公式给出一个更全局的视角来观察一层神经元的激活是如何与上一层神经元的激活联系起来的:先将权重矩阵应用到上一层的激活,再加上偏置向量,最后过激活函数。
我们引入中间变量 ,我们将 称为第 层神经元的加权输入 (weighted input)。其元素为:
2.2 反向传播的四个基本等式

右边的第一项表示第 个输出激活多大程度上影响了损失函数。如果损失函数不太依赖于第 个神经元激活,那么 会是一个比较小的值。第二项表示激活函数在 上的改变程度。
将上式改写为矩阵形式:
证明:
从定义出发,应用多元微积分的链式法则:
2.2.2 误差与下一层误差的关联

上式中, 是第 层权重矩阵 的转置。这个式子乍一看是很复杂的,但每一项都有优美的解释。假设我们已经知道第 层的误差 ,乘以转置的权重矩阵 ,可以理解为将误差通过网络反向传播,这衡量了第 层输出激活的误差;再乘以阿达玛乘积 ,将误差通过第 层的激活函数反向传播,这衡量了第 层加权输入的误差。
这个式子是很优雅的。有了公式(BP1)和(BP2),就可以计算出所有层对加权输入的误差了。 。这也就是称之为梯度反向传播算法的原因。
证明:
从定义出发,应用多元微积分的链式法则: 有 , 以及 。
要评估等式右边的第一项,注意到:
取微分,得到:
带入上上式中,得到:
重写为矩阵形式,即:
2.2.3 偏置的梯度

第 层偏置的梯度就等于第 层加权输入的误差 。改写为矩阵形式:
证明:
由定义出发,用多元微积分的链式法则:
注意到: ,故 。带入上式中,得到:
2.2.4 权重的梯度

第 层权重的梯度就等于第 层加权输入的误差 与 上一层神经元输出激活 的乘积。将上式改写为:
假设权重 连接了两个神经元, 是神经元输入给权重的激活, 是权重输出给神经元的误差。

证明:
由定义出发,应用多元微积分的链式法则:
注意到: ,故 。带入上式中,得到:
2.2.5 四个基本等式
综上,梯度反向传播的四个基本等式是:
有了这四个基本等式,我们就基本理解了梯度的计算过程。
- 后向传递与前向传递的FLOPs比率
3.1 定义
FLOPS:全大写,floating point operations per second,每秒钟浮点数计算次数,理解为运算速度,是衡量硬件性能的指标。例如:A100的float32运算速度是9.7TFLOPS,V100的float32运算速度是7.8TFLOPS。
FLOPs:s为小写,floating point operations,表示浮点数运算次数,理解为计算量,衡量模型或算法的复杂度。
如何计算矩阵乘法的FLOPs呢? 对于 ,计算 需要进行 次乘法运算和 次加法运算,共计 次浮点数运算,需要 FLOPs。对于 ,浮点数运算次数为 。
backward-forward FLOP ratio:后向传递与前向传递的FLOPs比率,表示一次后向传递的浮点数计算次数与一次前向传递的浮点数计算次数的比率。衡量了一次后向传递要比一次前向传递多进行的浮点数运算。
3.2 前向传递与后向传递的浮点数操作次数的理论分析
为了理解后向传递的浮点数运算为什么要比前向传递多?我们就要从反向传播算法的四个基本等式入手。
我们从一个有2层隐藏层的神经网络入手:

我们假设线性层采用ReLU激活函数,采用随机梯度下降优化器。下表中h1和h2分别表示第1层和第2层隐藏层的神经元个数。有2层隐藏层的神经网络一次训练迭代的计算过程如下表所示:

从上表中,我们可以观察到,对于多层前馈神经网络模型,有以下结论:
1. 相比于线性层,激活函数ReLU和损失函数的浮点数运算量可以忽略。
2. 对于第一层,后向传递-前向传递的FLOPs比率是1:1。
3. 对于其他层,后向传递-前向传递的FLOPs比率是2:1。
- 采用随机梯度下降作为优化器,权重更新的FLOPs是模型参数规模的2倍。
3.2.1 第一层与其他层的区别
对于多层前馈神经网络模型,采用随机梯度下降作为优化器。
第一层的后向传递-前向传递的FLOPs比率是1:1,其他层的后向传递-前向传递的FLOPs比率是2:1。模型参数更新的FLOPs是模型参数规模的2倍。
3.2.2 batch_size的影响
前向传递和后向传递的计算量FLOPs与batch_size成正比,即随着batch_size增大而线性增长。
优化器更新模型参数的FLOPs与batch_size无关,只与模型参数规模和优化器类型有关。
随着batch_size增大,前向传递和后向传递的FLOPs线性增长,而权重更新的FLOPs保持不变,这使得权重更新的FLOPs变得逐渐可以忽略不计了。
3.2.3 网络深度的影响
神经网络层数对后向传递-前向传递FLOPs比率有着间接的影响。由于第一层的后向-前向FLOPs比率是1:1,而其他层后向-前向FLOPs比率是2:1。层数的影响实际上是第一层与其他层的比较。
定义一个CNN神经网络,中间层的数量由0到100,可以看到后向-前向FLOPs比率由1.5提高到了接近2的水平。当层数逐渐变深的时候,第一层对模型整体的FLOPs影响就变小了,模型整体的后向-前向FLOPs比率就很接近2。

4. 总结
随着batch_size的增大,前向传递和后向传递的FLOPs线性增长,而权重更新的FLOPs保持不变,参数更新的FLOPs变得可以忽略不计了。这体现为:当batch_size足够大时,在训练神经网络的一次迭代中,前向传递和后向传递是主要的耗时环节,而参数更新的耗时变得几乎可以忽略不计。
由于第一层的后向-前向FLOPs比率是1:1,而其他层后向-前向FLOPs比率是2:1。随着网络层数的加深,第一层对整体FLOPs的影响变得可以忽略不计了。这体现为:当网络层数足够深时,后向传递的耗时几乎是前向传递耗时的2倍。
总的来说,对于用大batch_size的深层神经网络来说,后向传递-前向传递的FLOPs比率接近于2:1,换句话说,后向传递的计算量大约是前向传递的两倍。
#RNN回归
Bengio新作大道至简与Transformer一较高下
近日,深度学习三巨头之一的Yoshua Bengio,带领团队推出了全新的RNN架构,以大道至简的思想与Transformer一较高下。
在Transformer统治的AI时代之下,散落在世界各地的「RNN神教」信徒,一直相信并期待着RNN回归的那天:
毕竟,凭借强大的顺序和上下文感知能力,RNN曾在各种任务中表现惊艳。
直到后来遭遇了反向训练的瓶颈,因Scaling Law而跌落神坛。
然而,人们并没有忘记RNN。
RWKV、Mamba、xLSTM等RNN衍生模型接连出现,欲挑战Transformer之霸主地位。
就在近日,又有重量级人物下场——
深度学习三巨头之一的Yoshua Bengio,带领团队推出了全新的RNN架构,以大道至简的思想与Transformer一较高下。
论文地址:https://arxiv.org/pdf/2410.01201v1
研究人员对传统的两种RNN架构LSTM和GRU,进行了大刀阔斧的改造,从中诞生了两个新模型:minLSTM和minGRU。
这俩极简主义的版本到底怎么样?咱们先看疗效。
首先是RNN最大的问题:训练速度。
上图展示了几种模型在T4 GPU上训练花费的时间,以及新模型带来的加速比。横轴为输入数据的序列长度,批量大小为64。
可以看到,相比于原版的LSTM和GRU,minLSTM、minGRU和Mamba的运行时间不会随序列长度而增加(后3个模型的线在左图中重叠了)。
当序列长度为4096时,新架构相对于传统版本达到了1300多倍的加速比!
相当于原版GRU需要3年才能做完的事情,minGRU一天就搞定了。
那么对线Transformer的战绩如何?
在本文测试的语言建模任务中,minGRU和minLSTM分别在600步左右达到最佳性能点。
相比之下,Transformer需要比minGRU多花大概2000步,训练速度慢了约2.5倍。
对此,YC上的网友表示:「我非常喜欢这个新架构的简单性」。
毕竟,俗话说的好,「最好的PR是那些删除代码的PR」。
模型架构
下面来感受一下极简模型的诞生过程。
首先,这是传统的RNN架构:
LSTM在RNN的每个cell中加入了比较复杂的门控:
三个门控(input gate、output gate、forget gate)和输入的分量,都通过线性投影和非线性激活函数来得出,并且依赖于上一个时刻的隐藏状态ht-1。
这些值再经过线性和非线性计算,得到本时刻的输出ct和隐藏状态ht。
GRU在LSTM的基础上做了一些简化:
少了显式计算ct,用于门控的项也缩减到2个,相应的参数量和计算量也减少了。
那么我们就从相对简单的GRU入手,开始改造。
改造的目的是使RNN能够应用并行扫描(Parallel Scan)算法,解决自身训练困难的问题。
简单来说,就是将网络中的计算改造成vt = at ⊙ vt−1 + bt的形式。
minGRU
第一步,公式中含有对之前隐藏状态ht-1的依赖,没办法用并行扫描,所以把ht-1直接删掉。
ht-1没了,负责调控ht-1的rt也没用了,删掉。
第二步,双曲正切函数(tanh)负责限制隐藏状态的范围,并减轻因sigmoid(σ)而导致的梯度消失。但是现在ht-1和rt都没了,tanh也失去了存在的意义,删掉。

那么最终,minGRU就是下面这三个公式:
相比于原版,参数量和计算量再次减少,最重要的是能够使用并行扫描来显著加快训练速度。
minLSTM
经过上面的叙述,minLSTM的由来就很好理解了。
首先还是去除隐藏状态的依赖:
接着是拿掉相关的tanh:

最后,为了保证LSTM输出的尺度与时间无关,以及hidden state在缩放上与时间无关,还需要删掉output gate。
output gate没了,ct也就没必要单独存在了,删掉;剩下的两个门控通过归一化来调配hidden state进入的比例。
——emmm......好像变成GRU了,算了不管了。
最终改造好的minLSTM是下面这个样子:
Were RNNs All We Needed?
全新的RNN搞出来了,能打Transformer吗?
别急,先打内战证明价值。
除了传统的RNN(LSTM和GRU),这里特别关注与Mamba的比较。
首先是训练上的提升:
实验在批次大小64的情况下改变序列长度,测量了模型执行前向传递、计算损失和向后传递计算梯度的总运行时间以及内存占用。
在运行时间方面,minLSTM、minGRU与Mamba实现了类似的效率。
序列长度为512时的运行时间(超过100次的平均值),分别为 2.97、2.72和2.71毫秒;序列长度为4096时,运行时间分别为3.41、3.25和3.15。
相比之下,LSTM和GRU的运行时间随序列长度线性增加。所以序列长度为512时,minGRU和minLSTM的训练加速了175倍和235倍;序列长度为4096时,加速比达到了1324和1361。
内存方面,利用并行扫描算法时会创建更大的计算图,所以minGRU、minLSTM和Mamba ,比传统RNN需要更多的内存(大概多出88%)。
——但这并不重要,因为对于RNN来说,训练时间才是瓶颈。
去除隐藏状态的效果
minLSTM和minGRU的训练效率是通过降低它们的门控对先前隐藏状态的依赖来实现的。
尽管单层minLSTM或minGRU的门控只与输入有关,而与时间无关,但是在深度学习中,模型是通过堆叠模块来构建的。
从第二层开始,minLSTM和minGRU的门也将与时间相关,从而对更复杂的函数进行建模。
下表比较了不同层数的模型在选择性复制任务上的性能。我们可以看到时间依赖性的影响:将层数增加会大大提高模型的性能。
训练稳定性
层数的另一个影响是稳定性,随着层数的增加,精度的方差减小。
此外,尽管minLSTM和minGRU都解决了选择性复制任务,但我们可以看到minGRU在经验上是一种比minLSTM更稳定的方法(更高的一致性和更低的方差)。
minLSTM丢弃旧信息并添加新信息,使用两组参数(forget gate 和input gate)控制比率。在训练期间,两组参数会向不同的方向进行调整,使得比率更难控制和优化。相比之下,minGRU的丢弃和添加信息由一组参数控制,更容易优化。
选择性复制
选择性复制任务的输入元素相对于其输出是随机间隔的,为了解决这项任务,模型需要执行内容感知推理,记住相关token并过滤掉不相关的token。
上表将minLSTM和minGRU与可以并行训练的知名RNN模型进行了比较(S4,H3,Hyena和Mamba(S6)),基线结果引自Mamba论文。
在所有这些基线中,只有Mamba的S6,以及本文的minGRU和minLSTM能够解决此任务,体现了LSTM和GRU的内容感知门控机制。
强化学习
下面开始对战Transformer。
考虑D4RL基准中的MuJoCo运动任务,包括三个环境:HalfCheetah、Hopper和Walker。
对于每个环境,模型在三个数据质量不同的数据集上进行训练:Medium(M)、Medium-Replay(M-R)和Medium-Expert(M-E)。
上表将minLSTM和minGRU与各种决策模型进行了比较,包括原始的Decision Transformer(DT)、Decision S4 (DS4) 、Decision Mamba和Aaren。
由结果可知,minLSTM和minGRU的性能优于Decision S4,与Decision Transformer、Aaren和Mamba相媲美(Decision S4的递归转换不是输入感知的,这会影响它的性能)。就平均分数而言,minLSTM和minGRU的表现优于除Decision Mamba之外的所有基线。
语言建模
最后考虑语言建模任务,使用nanoGPT框架在莎士比亚的作品上训练字符级GPT。
上图绘制了具有交叉熵损失的学习曲线,可以发现minGRU、 minLSTM、 Mamba和Transformers分别实现了1.548、1.555、1.575和1.547的可比测试损耗。
Mamba的表现略差于其他模型,但训练速度更快(400步),minGRU和minLSTM分别花费575步和625步。而Transformer直接比minGRU多了2000 步,慢了大概2.5倍。
参考资料:
https://arxiv.org/pdf/2410.01201v1
#全面总结机器学习超参数调优
超参数调优方法、工具以及基于AutoML和算法的超参数调优详解。
机器学习建模的超参数调优。
文章很长,建议直接收藏~
一、什么是机器学习超参数?
机器学习超参数是在开始学习过程之前设置值的参数,而不是通过训练得到的参数数据。
超参数是在模型训练之外设置的选项,不会在训练过程中被优化或更改。相反,需要在训练之前手动设置它们,并且对模型的性能有很大的影响。
二、为什么要进行机器学习超参数的调优?
在机器学习中,通常需要针对特定任务选择和调整超参数。例如,在支持向量机(SVM)中,有一个重要的超参数是正则化参数C,它可以控制模型复杂度并影响模型的泛化能力。在训练神经网络时,学习率和批次大小也是常见的超参数,它们可以影响模型的收敛速度和最终的预测效果。
机器学习超参数的调优是为了找到一组最佳的超参数组合,使模型在特定任务上表现最佳。超参数的调优对于提高模型性能、防止过拟合、加速收敛等方面都非常重要。
不同的超参数组合可以显著影响模型的性能,因此通过调优来找到最佳的超参数组合是非常必要的。
下文从网格搜索等直接调优方法、基于Optuna等调优工具、基于AutoML的调优、基于算法的调优等4个方面进行阐述。
三、超参数调优方法
常用的超参数调优方法有以下几种:
- 网格搜索(Grid Search):网格搜索是一种简单的超参数调优方法,它通过穷举指定的参数组合,计算每一组参数在验证集上的表现,最终选择表现最好的参数组合。
- 贝叶斯优化:贝叶斯优化是一种利用贝叶斯定理和最优化方法寻找全局最优解的优化算法,它适用于高维、高成本、有限样本的优化问题。
- 随机搜索(Random Search):随机搜索是一种基于随机采样的超参数调优方法,它通过在参数空间中随机选择参数组合,寻找最优解。
3.1 网格搜索Grid Search
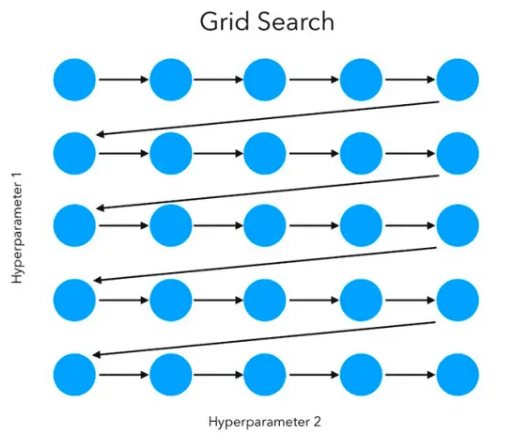
1、什么是网格搜索
网格搜索(Grid Search)是一种超参数调优方法,它通过穷举指定的参数组合,计算每一组参数在验证集上的表现,最终选择表现最好的参数组合。
https://pyimagesearch.com/2021/05/24/grid-search-hyperparameter-tuning-with-scikit-learn-gridsearchcv/
网格搜索是一种简单而有效的调优方法,常用于确定最佳的超参数组合。
2、网格搜索的python实战
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
from sklearn.datasets import load_iris
# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target
# 定义模型
svm = SVC(kernel='linear', C=100, gamma='auto')
# 定义网格搜索参数范围
param_grid = {
'C': [0.1, 1, 10, 100],
'gamma': [1e-3, 1e-2, 1e-1, 1],
}
# 创建网格搜索对象
grid_search = GridSearchCV(svm, param_grid, cv=5)
# 对数据进行网格搜索
grid_search.fit(X, y)
# 输出最佳参数组合和对应的得分
print('Best parameters:', grid_search.best_params_)
print('Best score:', grid_search.best_score_)- 使用了Scikit-learn库中的GridSearchCV类来实现网格搜索
- 定义了一个参数网格(param_grid),其中包含了C和gamma两个超参数的不同取值组合
- 创建了一个GridSearchCV对象,并将参数网格、SVM模型和交叉验证(cv)参数传入
- 使用best_params_和best_score_属性输出最佳参数组合和对应的得分
3.2 随机搜索Random Search
1、什么是随机搜索
随机搜索是一种优化方法,它通过在允许的范围内随机生成点来搜索可能的解决方案,并计算每个点的目标函数值。然后,它根据目标函数值选择下一个点进行搜索,以逐步接近最优解。
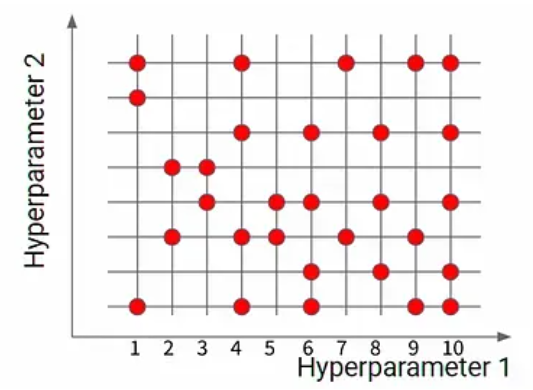
这种方法适用于处理高维、非线性、非凸或非连续的优化问题,特别是当精确解的计算成本非常高时。
2、基于随机搜索的python实战
import numpy as np
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target
# 定义随机搜索函数
def random_search(X, y, model, param_space, iteration_num):
best_score = -1
best_params = None
for i in range(iteration_num):
# 从参数空间中随机采样一组超参数
params = {k: v[np.random.randint(len(v))] for k, v in param_space.items()}
# 训练模型并计算验证集上的准确率
model.set_params(**params)
score = model.score(X[:100], y[:100])
# 更新最优解
if score > best_score:
best_score = score
best_params = params
return best_score, best_params
# 定义随机森林分类器模型
model = RandomForestClassifier()
# 定义超参数空间
param_space = {
'n_estimators': [100, 200, 300, 400, 500],
'max_depth': [2, 3, 4, 5, 6],
'max_features': ['auto', 'sqrt', 'log2'],
'bootstrap': [True, False]
}
# 执行随机搜索
best_score, best_params = random_search(X, y, model, param_space, 100)
print('最佳准确率:', best_score)
print('最佳超参数:', best_params)- 使用随机森林分类器模型,并定义了四个需要优化的超参数:n_estimators、max_depth、max_features和bootstrap
- 从参数空间中随机采样100组超参数,然后使用验证集上的准确率来评估这些超参数的优劣,最终输出最佳准确率和对应的最佳超参数
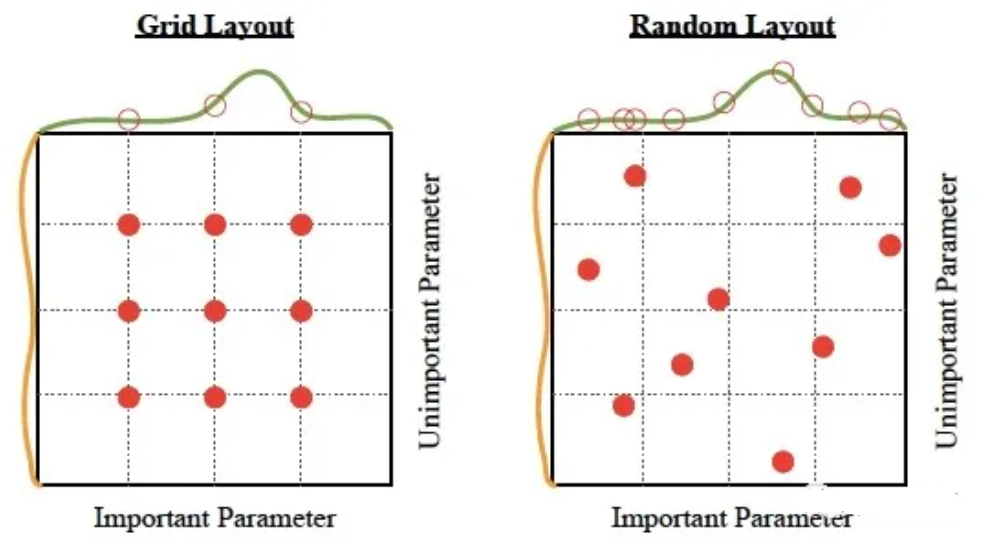
网格搜索优化和随机搜索优化的对比:
3.3 贝叶斯优化
1、什么是贝叶斯优化
贝叶斯优化是一种黑盒优化算法,用于求解表达式未知的函数的极值问题。它基于贝叶斯定理,通过构建概率模型来描述目标函数的后验分布,并利用这个模型来选择下一个采样点,以最大化采样价值。
其核心思想是利用高斯过程回归(Gaussian Process Regression, GPR)来建模目标函数的分布。GPR认为目标函数是由一系列训练数据点(输入和输出)所构成的随机过程,通过高斯概率模型来描述这个随机过程的概率分布。贝叶斯优化通过不断地添加样本点来更新目标函数的后验分布,直到后验分布基本贴合真实分布。
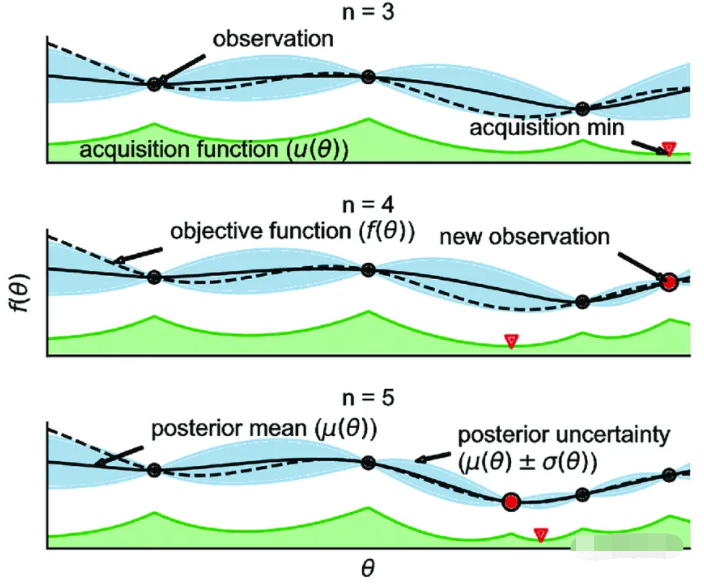
贝叶斯优化有两个核心过程:
- 先验函数(Prior Function, PF):PF主要利用高斯过程回归来建模目标函数的先验分布
- 采集函数(Acquisition Function, AC):AC主要包括 Expected Improvement(EI)、Probability of Improvement(PI)和 Upper Confidence Bound(UCB)等方法,用于衡量每一个点对目标函数优化的贡献,并选择下一个采样点。
贝叶斯优化在机器学习种被用于AutoML算法,自动确定机器学习算法的超参数。它也是一种全局极值搜索方法,特别适用于高维非线性非凸函数,具有较好的效果和效率。
贝叶斯优化以函数被视为一个满足某种分布的随机过程,通过在定义域内求函数值,使用贝叶斯公式更新对分布的估计,然后根据新的分布找到最可能的极值点位置,从而提高对函数及其极值的估计的精确性。
2、贝叶斯优化的python实战
import numpy as np
from scipy.optimize import minimize
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, ConstantKernel as C
# 定义目标函数
def f(x):
return np.sin(5 * x) + np.cos(x)
# 定义高斯过程回归模型
kernel = C(1.0, (1e-3, 1e3)) * RBF(10, (1e-2, 1e2))
gpr = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10)
# 定义贝叶斯优化函数
def bayesian_optimization(X_train, y_train, X_test):
# 训练高斯过程回归模型
gpr.fit(X_train, y_train)
# 计算测试集的预测值和方差
y_pred, sigma = gpr.predict(X_test, return_std=True)
# 计算期望改进(Expected Improvement)
gap = y_pred - f(X_test)
improvement = (gap + np.sqrt(sigma ** 2 + 1e-6) * np.abs(gap).mean()) * 0.5
# 计算高斯过程回归模型的超参数
result = minimize(gpr.kernel_, np.zeros(gpr.kernel_.shape[0]), method='L-BFGS-B')
hyperparameters = result.x
# 输出最优超参数和对应的期望改进值
return hyperparameters, improvement.max()
# 定义贝叶斯优化的迭代次数和采样点数量
n_iter = 20
n_samples = 5
# 进行贝叶斯优化
results = []
for i in range(n_iter):
# 在定义域内随机采样n_samples个点
X_train = np.random.uniform(-2 * np.pi, 2 * np.pi, (n_samples, 1))
y_train = f(X_train)
# 进行贝叶斯优化并记录最优超参数和对应的期望改进值
result = bayesian_optimization(X_train, y_train, X_test=np.random.uniform(-2 * np.pi, 2 * np.pi, (100, 1)))
results.append(result)
print('Iter: {}, Hyperparameters: {:.2f}, Expected Improvement: {:.4f}'.format(i, result[0][0], result[1]))- 定义目标函数f
- 使用高斯过程回归模型(GPR)来建模目标函数的分布
- 定义贝叶斯优化函数bayesian_optimization;其中训练集、测试集和采样点数作为输入,输出最优的超参数和对应的期望改进值
- Expected Improvement作为采集函数,通过不断地添加样本点来更新目标函数的后验分布,并使用L-BFGS-B方法来最小化高斯过程回归模型的超参数
四、基于超参数调优工具4.1 什么是超参数优化库?
超参数优化库(Hyperparameter Optimization Library)是一种用于自动化超参数优化的软件库或工具。这些库使用不同的算法和技术,以实现自动化超参数搜索和优化过程。
超参数优化库通常提供易于使用的接口,允许用户定义要优化的超参数和目标函数。它们使用不同的算法和技术,如网格搜索、随机搜索、遗传算法、贝叶斯优化等,以搜索和优化超参数空间。这些库的目标是减少人工调整超参数的工作量,提高模型性能,并加速机器学习模型的训练过程。
4.2 常见的超参数优化工具
以下是几个常用的超参数优化库:
- scikit-Opitimize
- Hyperopt
- Optuna
- Spearmint
- Gaussian Process-based Hyperparameter Optimization (GPGO)
- Ray Tune
- GPyOpt
- SigOpt
- Keras Tuner
这些库都提供了不同的算法和工具,以实现超参数优化,并具有不同的特点和优点。您可以根据您的需求选择最适合您的库。
4.3 Scikit-Optimize库
1、Scikit-Optimize库简介
Scikit-optimize 是一个 Python 库,用于执行基于scipy的优化算法。它旨在提供一种简单而有效的工具,用于机器学习和科学计算的优化问题。Scikit-optimize 提供了许多不同的优化算法,包括梯度下降、随机搜索、贝叶斯优化等。
Scikit-optimize 提供了许多预定义的搜索空间和目标函数,以便轻松地设置超参数优化任务。用户可以定义自己的搜索空间和目标函数,以适应特定的机器学习模型和任务。Scikit-optimize 还提供了可视化工具,可以帮助用户更好地理解优化过程和结果。
2、基于python的Scikit-Optimize库优化实战
import numpy as np
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from skopt import gp_minimize
# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 定义机器学习模型
clf = RandomForestClassifier()
# 定义搜索空间和目标函数
search_space = {
'n_estimators': [100, 200, 500],
'max_depth': [3, 5, None],
'max_features': ['auto', 'sqrt', 'log2']
}
def objective(x):
clf.set_params(**{search_space[name]: x[name] for name in x})
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
return -accuracy_score(y_test, y_pred)
# 执行优化算法
res = gp_minimize(objective, search_space, n_calls=20, random_state=42)
# 输出最优超参数组合和对应的验证准确率
print("Best hyperparameters:", res.x)
print("Max validation accuracy:", res.fun)4.4 Hyperopt库
1、Hyperopt库简介
Hyperopt是一个Python库,用于对机器学习模型的算法进行智能搜索。它主要使用三种算法:随机搜索算法、模拟退火算法和TPE(Tree-structured Parzen Estimator)算法。
安装Hyperopt库:可以使用pip命令来安装Hyperopt库:
pip install hyperopt使用步骤:
- 准备目标函数:目标函数应该是一个可优化的函数,它接受一个超参数列表作为输入,并返回一个标量值。在Hyperopt中,使用fn来指定目标函数。
- 定义超参数搜索空间:使用Hyperopt的hp模块定义超参数的搜索空间。可以使用hp.choice、hp.uniform等函数来定义不同类型的超参数。
- 使用fmin函数进行优化:使用Hyperopt的fmin函数进行优化,该函数接受目标函数、超参数搜索空间和优化算法作为输入,并返回最佳的超参数组合。
官方学习地址:https://github.com/hyperopt/hyperopt
2、基于python优化的实战案例
from hyperopt import hp, fmin, tpe
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 定义目标函数
def objective(params):
clf = SVC(kernel=params['kernel'], C=params['C'], gamma=params['gamma'])
clf.fit(X_train, y_train)
score = clf.score(X_test, y_test)
return -score # 因为Hyperopt需要最小化目标函数,所以我们需要将准确率取反
# 定义超参数搜索空间
space = {
'kernel': hp.choice('kernel', ['linear', 'poly', 'rbf', 'sigmoid']),
'C': hp.uniform('C', 0.001, 10),
'gamma': hp.uniform('gamma', 0.001, 10)
}
# 使用贝叶斯优化进行超参数搜索
best = fmin(fn=objective, space=space, algo=tpe.suggest, max_evals=100)
print('Best parameters: ', best)4.5 Optuna库
1、Optuna库简介
Optuna是一个用于超参数优化的库,它支持定义目标函数,搜索超参数空间并自动进行优化。
可以使用pip命令来安装Optuna库:
pip install Optuna使用步骤:
- 定义搜索空间:使用Optuna提供的分布函数来定义超参数的搜索空间。例如,对于一个取值范围为[0, 1]的浮点数,可以使用uniform函数来定义该超参数的搜索空间。
- 定义目标函数:目标函数是需要优化的模型,可以是任何可调用对象,如Python函数、类方法等。目标函数的输入是超参数的值,输出是模型的性能指标。
- 创建Optuna试验:创建Optuna试验对象,并指定目标函数和搜索算法。
- 运行Optuna试验:运行Optuna试验,进行超参数搜索。在每次试验结束后,Optuna会更新超参数的取值,并记录当前试验的性能指标。可以设置尝试的次数或时间,来控制搜索空间的大小和搜索时间的限制。
- 分析试验结果:在试验结束后,可以使用Optuna提供的可视化工具来分析试验结果,并选择最优的超参数组合。
2、基于python的使用案例
import numpy as np
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import SGDRegressor
# 生成数据集
X, y = make_regression(n_samples=100, n_features=1, noise=0.1)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 定义目标函数
def objective(trial):
# 定义超参数
learning_rate = trial.suggest_float('learning_rate', 1e-10, 1e-5)
batch_size = trial.suggest_int('batch_size', 32, 256)
optimizer = trial.suggest_categorical('optimizer', ['sgd', 'adam'])
# 创建模型
model = SGDRegressor(learning_rate=learning_rate, batch_size=batch_size, optimizer=optimizer)
# 训练模型
model.fit(X_train, y_train)
# 计算性能指标
loss = np.mean((model.predict(X_test) - y_test) ** 2)
return loss
# 创建Optuna的study对象,并指定需要优化的目标函数和搜索空间
import optuna
study = optuna.create_study()
study.optimize(objective, n_trials=100)
# 最佳的超参数组合
print(study.best_params) # 输出最佳的超参数组合
print(study.best_value) # 输出最佳的性能指标值4.6 Spearmint库
1、Spearmint库简介
Spearmint是一个用于优化贝叶斯推断的库。它基于论文《实用贝叶斯优化》中概述的算法。该库可用于执行贝叶斯优化,这是一种用于全局优化的算法,主要用于寻找最小化目标函数的配置。(建议少使用)
https://github.com/JasperSnoek/spearmint
Spearmint库提供了一种表达和优化贝叶斯推断问题的方式。它允许用户定义目标函数以及用于描述优化问题的约束和边界。库中的核心算法则负责根据这些定义来优化目标函数。Spearmint库的优点包括:
- 灵活的目标函数表达:Spearmint支持多种类型的数据和复杂的模型结构,使得用户可以灵活地表达各种目标函数。
- 高性能:Spearmint通过高效的实现和优化算法来提高运行速度,从而能够处理大规模的数据集和复杂的模型。
- 易于使用:Spearmint提供了简单易用的接口,使得用户可以轻松地配置和运行优化任务。
- 社区支持:Spearmint是由一个活跃的社区支持的开源项目,这意味着用户可以获得来自其他开发者的反馈和支持。
2、基于Spearmint的实战案例
import numpy as np
import spearmint as sp
from scipy.stats import norm
# 定义目标函数
def objective(x):
# 假设目标函数是一个简单的二次函数,其中x是一个向量
return x[0]**2 + x[1]**2
# 定义Spearmint的优化器
spearmint = sp.Spearmint()
# 设置要优化的参数范围
var_names = ['var1', 'var2']
bounds = [[-5, 5], [-5, 5]]
priors = [sp.priors.NormalPrior(0, 1), sp.priors.NormalPrior(0, 1)]
# 运行贝叶斯优化,设置最大迭代次数为10次
results = spearmint.optimize(objective, var_names, bounds, priors, n_iter=10)
# 输出最优的参数组合和对应的函数值
print('最优参数组合:', results.x)
print('最优函数值:', results.func)4.7 GPGO库
1、GPGO简介
GPGO全称是Gaussian Process Optimization for Hyperparameters Optimization,是Google的超参数优化库,它使用Gaussian Processes(高斯过程)进行超参数优化,专为TensorFlow和Keras而设计。
高斯过程是一种强大的非参数贝叶斯模型,它为超参数优化提供了一种概率框架,可以自动管理探索与利用的权衡。
使用之前先安装:
pip install gpgo使用步骤:
- 首先,需要定义要优化的目标函数(例如,神经网络的训练损失)。
- 其次,需要定义搜索空间,即超参数的可能取值范围。
- 然后,使用GPGO运行优化过程。在每次迭代中,优化器会选择一组超参数,并使用目标函数评估该组超参数的性能。
- 最后,优化器会根据评估结果更新其关于最佳超参数的信念,并继续搜索,直到达到预设的终止条件(例如,达到最大迭代次数或找到满意的超参数组合)。
2、python实战案例
import numpy as np
import tensorflow as tf
from tensorflow.keras.datasets import mnist
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten
from gpgo import GPGO
# 加载MNIST数据集
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# 数据缩放
x_train = x_train / 255.0
x_test = x_test / 255.0
# 1-定义神经网络模型
model = Sequential([
Flatten(input_shape=(28, 28)),
Dense(128, activatinotallow='relu'),
Dense(64, activatinotallow='relu'),
Dense(10)
])
#2- 定义优化目标函数(即神经网络的训练损失)
def loss_fn(y_true, y_pred):
return tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_true, logits=y_pred))
# 3-定义优化器并设置超参数的搜索空间
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-4)
hyperparams = {
'kernel__lgcp': [5, 10, 20],
'kernel__scale': [1e-4, 1e-3, 1e-2],
'kernel__lengthscale': [1., 5., 10.]
}
# 4-创建GPGO优化器并运行优化过程
gpgo = GPGO(optimizer=optimizer, loss_fn=loss_fn, hyperparams=hyperparams, datasets=(x_train, y_train), epochs=10)
best_params, best_loss = gpgo.run()- 加载MNIST数据集并定义了一个简单的神经网络模型
- 定义了优化目标函数,即神经网络的训练损失
- 创建了一个GPGO优化器,并将超参数的搜索空间传递给它
- 使用
run方法运行优化过程,并输出最佳超参数和最低的训练损失
4.8 Ray Tune库
1、简介
Ray Tune是Ray的一个超参数优化库,可以用于优化深度学习模型的性能。它基于Scikit-learn和Google Vizier的接口,并提供了简单易用的API来定义和运行超参数搜索实验。
Ray Tune的特性包括:
- 支持多种超参数优化算法,如网格搜索、随机搜索和贝叶斯优化等。
- 可以自动管理实验的进度和结果,提供清晰的可视化界面。
- 可以轻松扩展到分布式环境,支持多节点并行超参数搜索。
- 与Ray框架无缝集成,可以轻松扩展到其他Ray任务中。
官方学习地址:https://docs.ray.io/en/latest/tune/index.html
2、官网提供的优化实战案例:
from ray import tune
def objective(config): # 1-定义目标优化函数
score = config["a"] ** 2 + config["b"]
return {"score": score}
search_space = { # 2-定义超参数搜索空间
"a": tune.grid_search([0.001, 0.01, 0.1, 1.0]),
"b": tune.choice([1, 2, 3]),
}
tuner = tune.Tuner(objective, param_space=search_space) # 3-执行搜索过程
results = tuner.fit()
print(results.get_best_result(metric="score", mode="min").config) # 最佳超参数组合4.9 Bayesian Optimization库
1、简介
Bayesian optimization,也称为Bayesian experimental design或sequential design,是一种使用贝叶斯推理和高斯过程(Gaussian process)的全局优化技术。它是一种在尽可能少的迭代次数内找到一个未知函数的最大值或最小值的方法,特别适合优化高成本函数或在勘探和开发之间需要平衡的情况。
官方学习地址:https://github.com/bayesian-optimization/BayesianOptimization
先安装:
pip install bayesian-optimization2、python实战案例
import numpy as np
from sklearn.gaussian_process import GaussianProcessRegressor
from scipy.optimize import minimize
# 定义目标函数
def target_function(x):
return np.sin(5 * x) + np.cos(2 * x) + np.random.normal(0, 0.1, size=x.shape)
# 定义高斯过程模型
def gpr_model(X, y):
kernel = 1.0 * np.eye(X.shape[0]) + 0.5 * np.ones((X.shape[0], X.shape[0]))
gpr = GaussianProcessRegressor(kernel=kernel)
gpr.fit(X, y)
return gpr
# 定义Bayesian Optimization函数
def bayesian_optimization(n_iterations, n_initial_points):
# 初始化数据点
x_initial = np.random.uniform(-5, 5, n_initial_points)
y_initial = target_function(x_initial)
# 初始化高斯过程模型
X_train = np.vstack((x_initial, x_initial))
y_train = np.vstack((y_initial, y_initial))
gpr = gpr_model(X_train, y_train)
# 进行n_iterations次迭代
for i in range(n_iterations):
# 使用EI策略选择新的数据点
acquisition_func = gpr.predictive_mean + np.sqrt(gpr.predictive_covariance(x_initial)[:, None, None]) * np.random.randn(*x_initial.shape)
EI = -gpr.negative_log_predictive_density(y_initial, acquisition_func)
x_new = x_initial[np.argmax(EI)]
y_new = target_function(x_new)
X_train = np.vstack((X_train, x_new))
y_train = np.vstack((y_train, y_new))
gpr = gpr_model(X_train, y_train)
x_initial = np.vstack((x_initial, x_new))
y_initial = np.vstack((y_initial, y_new))
print("Iteration {}: Best value = {} at x = {}".format(i+1, np.min(y_initial), np.argmin(y_initial)))
return x_initial[np.argmin(y_initial)], np.min(y_initial)
# 运行Bayesian Optimization函数并输出结果
best_x, best_y = bayesian_optimization(n_iterations=10, n_initial_points=3)
print("Best x = {}, best y = {}".format(best_x, best_y))- 定义了一个目标函数
target_function,该函数是一个带有随机噪声的正弦和余弦函数的组合; - 定义了一个高斯过程模型
gpr_model,该模型使用一个常数核来构建高斯过程; - 定义了一个
bayesian_optimization函数,该函数使用贝叶斯优化算法来找到目标函数的最大值; - 最后调用
bayesian_optimization函数并输出结果
4.10 GPyOpt库
1、简介
GPyOpt是一个基于GPy的Python库,用于实现贝叶斯优化。它提供了灵活的框架,可以处理具有各种类型代理模型(如高斯过程和随机森林)的优化问题。
GPyOpt库旨在解决实际问题,包括但不限于函数优化、超参数优化、深度学习中的模型调参等。使用者可以根据需要自定义代理模型,并且能够方便地与第三方库集成。此外,GPyOpt支持多种优化算法,如贝叶斯优化、粒子群优化等,以满足不同应用场景的需求。
官方学习地址:https://sheffieldml.github.io/GPyOpt/
直接使用pip进行安装:
pip install gpyopt基于源码的安装:
# git clone https://github.com/SheffieldML/GPyOpt.git
# cd GPyOpt
# git checkout devel
# nosetests GPyOpt/testing3个主要依赖包的版本要求:
- GPy (>=1.0.8)
- numpy (>=1.7)
- scipy (>=0.16)
2、基于python的使用案例
使用GPyOpt库来解决一个简单的函数优化问题:尝试找到函数的最大值
import numpy as np
from gpyopt import Optimizer
# 定义目标函数
def f(x):
return -x**2
# 定义初始点
x0 = np.array([0.0])
# 定义优化器
optimizer = Optimizer(f=f, x0=x0)
# 设置优化选项
optimizer.set_verbose(True) # 设置是否输出优化信息
optimizer.set_stop_condition(stop='max_iter', value=100) # 设置最大迭代次数和停止条件
# 运行优化
optimizer.optimize()
# 输出结果
print('最优解:', optimizer.x_opt)
print('最优值:', optimizer.f_opt)4.11 SigOpt库
1、简介SigOpt超参数优化库是一个用于优化机器学习模型的软件库。SigOpt的优化算法使用贝叶斯优化,这是一种用于寻找全局最优的优化算法,通常用于寻找深度学习模型中的最佳超参数组合。
SigOpt的API使得调整模型超参数变得容易,并且可以与许多不同的机器学习库(包括TensorFlow、PyTorch、Scikit-learn等)集成。SigOpt还提供了一个可视化界面,可以帮助用户监控和调整优化过程。通过使用SigOpt,开发人员可以更快地找到最佳超参数组合,提高模型的性能和准确性。
官方学习地址:https://docs.sigopt.com/intro/main-concepts
基于pip的安装:
pip install sigopt2、基于python的实战案例
import torch
import torch.nn as nn
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
# 优化相关
import sigopt
from sigopt.api import create_run
from sigopt.config import get_version_id
from sigopt.local import local_experiment
from sigopt.run import run_fn, get_default_args, get_default_config, get_default_options, get_default_suggestion_callback, run_in_notebook, run_in_script, run_in_jupyter_notebook # 用于定义运行函数和运行环境
from sigopt.suggestion import get_suggestion, get_suggestion_from_web # 用于获取建议的超参数值
# 定义学习率和批量大小
space = {
"learning_rate": (1e-5, 1e-2, "log-uniform"),
"batch_size": (32, 256, "uniform")
}
# 定义基于pytorch的深度学习模型
class SimpleModel(nn.Module):
def __init__(self):
super(SimpleModel, self).__init__()
self.fc = nn.Linear(784, 10)
def forward(self, x):
x = x.view(-1, 784)
x = self.fc(x)
return x
# 加载mnist数据集
transform = transforms.Compose([
transforms.ToTensor(), # 转成张量
transforms.Normalize((0.1307,), (0.3081,)) # 数据标准化
])
train_dataset = datasets.MNIST(root="data", train=True, transform=transform, download=True)
train_loader = DataLoader(train_dataset, batch_size=128, shuffle=True)
# 优化过程
def objective(config): # 定义优化目标函数,即模型的准确率
model = SimpleModel() # 创建模型实例
optimizer = torch.optim.Adam(model.parameters(), lr=config["learning_rate"]) # 创建优化器并设置学习率
criterion = nn.CrossEntropyLoss() # 创建损失函数
train_loss = 0.0
correct = 0.0
total = 0.0
for i, data in enumerate(train_loader, 0): # 对训练集进行迭代,计算损失和准确率
inputs, labels = data # 获取输入和标签数据
optimizer.zero_grad() # 清零梯度缓存
outputs = model(inputs) # 前向传播,计算输出张量
loss = criterion(outputs, labels) # 计算损失张量
loss.backward() # 反向传播,计算梯度张量并更新权重参数
train_loss += loss.item() # 累加损失值并计算平均损失值和准确率
_, predicted = torch.max(outputs.data, 1) # 找到最大概率的标签作为预测结果并计算准确率
total += labels.size(0) # 累加样本数以计算总体准确率
correct += predicted.eq(labels.data).cpu().sum() # 累加正确预测的样本数并计算准确率
accuracy = correct / total # 计算总体准确率并返回给优化器作为目标函数值
return accuracy, {"learning_rate": config["learning_rate"], "batch_size": config["batch_size"]} # 将目标函数值和超参数值返回给优化器4.12 Keras Tuner
KerasTuner是一个易于使用的分布式超参数优化框架,能够解决执行超参数搜索时的一些痛点。它利用高级搜索和优化方法,如HyperBand搜索和贝叶斯优化,来帮助找到最佳的神经网络超参数。
安装命令:
pip install keras-tuner --upgrade官方学习地址:https://keras.io/keras_tuner/2、实战案例
import keras_tuner
from tensorflow import keras
# 定义网络模型
def build_model(hp):
model = keras.Sequential()
model.add(keras.layers.Dense(
hp.Choice("units", [8,16,32]),
activatinotallow="relu"
))
model.add(keras.layers.Dense(1,activatinotallow="relu"))
model.compile(loss="mse")
return model
tuner = keras_tuner.RandomSearch(
build_model,
objective="val_loss",
max_trials=5
)
tuner.search(x_train, y_train, epochs=5, validation_data=(x_val, y_val))完整案例:https://www.analyticsvidhya.com/blog/2021/06/tuning-hyperparameters-of-an-artificial-neural-network-leveraging-keras-tuner/
五、基于AutoML库的超参数调优
5.1 什么是AutoML库
自动化机器学习库(AutoML)是一种软件工具或库,旨在自动化机器学习工作流程。这些库使用不同的算法和技术,以实现自动化机器学习任务的过程,包括数据预处理、特征选择、模型选择、参数优化、模型评估等。
AutoML的目的是简化机器学习的过程,使非专业人士也可以应用机器学习,或者帮助专业人士更高效地处理机器学习任务。这些库通常提供易于使用的接口,并且能够处理大规模的数据集。
5.2 常见的自动化机器学习库
自动化机器学习库有以下几种:
- Auto-Sklearn。Auto-Sklearn是基于scikit-learn软件包构建的开源AutoML库。它为给定的数据集找到最佳性能的模型以及最佳的超参数集。它包括一些特征工程技术,例如单点编码,特征归一化,降维等。该库适用于中小型数据集,不适用大型数据集。
- H2O AutoML。H2O AutoML是一个完整的端到端的机器学习自动化工具,可以处理各种类型的数据集,包括小数据和大数据,标准数据和非标准数据。它实现了整个机器学习流程的自动化,包括数据准备,模型选择,特征选择,模型优化等。
- Auto-Keras。Auto-Keras是一个基于Keras深度学习框架的自动机器学习库。它旨在为深度学习模型提供高度自动化的设计和训练流程,以解决用户在面对不同任务时可能需要重复编写大量代码的问题。
- AutoGluon。AutoGluon是一个开源的深度学习自动机器学习库,由AWS团队开发和维护。它旨在帮助开发者自动完成机器学习的所有过程,包括数据预处理、特征工程、模型选择和超参数调整等。AutoGluon使用了一种称为“神经架构搜索”的技术来自动化地选择最佳的模型架构。
- Pycaret。PyCaret 是一个开源的、低代码的机器学习库,旨在简化机器学习工作流并提高工作效率。它是一个 Python 库,封装了多个流行的机器学习库和框架,如 scikit-learn、XGBoost、LightGBM、CatBoost、spaCy、Optuna、Hyperopt、Ray 等。PyCaret 还提供了一套简单易用的 API,可以帮助你完成各种机器学习任务,包括数据预处理、模型训练、评估和部署等。
- MLBox。MLBox是一个功能强大的自动化机器学习库,旨在为机器学习工程师和研究者提供一站式的机器学习解决方案。它是由国内的一家公司开发的,封装了多种流行的机器学习算法和框架,如scikit-learn、XGBoost、LightGBM、CatBoost、spaCy、Optuna、Hyperopt、Ray等,并将它们整合到一个统一的框架中,提供了简单易用的API,使得机器学习的流程变得更加高效和便捷。
- Auto-PyTorch。Auto-PyTorch是一个基于PyTorch的自动机器学习库。它旨在为超参数搜索和模型选择提供自动化的解决方案,以帮助用户在训练深度学习模型时提高效率和准确性。
5.3 Auto-Sklearn
1、简介
Auto-Sklearn是一个开源的AutoML库,它利用流行的Scikit-Learn机器学习库进行数据转换和机器学习算法。Auto-Sklearn是由Matthias Feurer等人开发的。在他们的2015年题为“efficient and robust automated machine learning”的论文中进行了描述。
Auto-Sklearn通过元学习(meta-learning)或梯度增强来自动选择最佳的学习算法及其超参数。它还可以自动调整模型的复杂性和集成度,以及执行数据预处理和后处理。安装命令:
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple auto-sklearn官方学习地址:https://automl.github.io/auto-sklearn/master/
2、案例学习
import autosklearn.classification # 基于自动化机器学习库的分类模型
import sklearn.model_selection
import sklearn.datasets
import sklearn.metrics
if __name__ == "__main__":
X, y = sklearn.datasets.load_digits(return_X_y=True)
# 数据切分
X_train, X_test, y_train, y_test = sklearn.model_selection.train_test_split(X, y, random_state=1)
# 基于自动化机器学习库的分类模型
automl = autosklearn.classification.AutoSklearnClassifier()
# 模型训练和预测
automl.fit(X_train, y_train)
y_hat = automl.predict(X_test)
print("Accuracy score", sklearn.metrics.accuracy_score(y_test, y_hat))5.4 H2O AutoML
1、简介
H2O AutoML是一款由H2O.ai开发的自动化机器学习工具。它通过自动化机器学习领域中的流程和技术,使得数据分析师和科学家们能够更快、更容易地构建高质量的预测模型。
H2O AutoML支持多种算法和模型选择,包括基于树的方法、线性模型和深度学习模型等。该工具还提供了自动特征工程、模型交叉验证和超参数优化等功能,可以帮助用户自动地进行数据清洗、特征工程、模型选择和调优等过程,从而提高模型的准确性和效率。
官网学习地址:https://docs.h2o.ai/h2o/latest-stable/h2o-docs/automl.html
2、使用案例
import h2o
from h2o.automl import H2OAutoML
# 启动H2O
h2o.init()
# 导入一个二分类数据集
train = h2o.import_file("https://s3.amazonaws.com/erin-data/higgs/higgs_train_10k.csv")
test = h2o.import_file("https://s3.amazonaws.com/erin-data/higgs/higgs_test_5k.csv")
x = train.columns
y = "response"
x.remove(y)
# 转成向量
train[y] = train[y].asfactor()
test[y] = test[y].asfactor()
# 训练模型:最多20个基线模型
aml = H2OAutoML(max_models=20, seed=1)
aml.train(x=x, y=y, training_frame=train)
# 查看模型效果
lb = aml.leaderboard
lb.head(rows=lb.nrows)
# 预测
preds = aml.predict(test)
# preds = aml.leader.predict(test)
# 模型排行输出
lb = h2o.automl.get_leaderboard(aml, extra_columns = "ALL")获取单个模型的效果:
m = aml.leader
# 等效
m = aml.get_best_model()
# 使用非默认指标获取最佳模型
m = aml.get_best_model(criterinotallow="logloss")
# 基于默认的排序指标获取XGBoost模型
xgb = aml.get_best_model(algorithm="xgboost")
# 基于logloss指标获取 XGBoost
xgb = aml.get_best_model(algorithm="xgboost", criterinotallow="logloss")
# 指定获取某个特殊的模型
m = h2o.get_model("StackedEnsemble_BestOfFamily_AutoML_20191213_174603")
# 获取模型的参数信息
xgb.params.keys()
# 特定参数
xgb.params['ntrees']获取H2O的训练日志及时间信息:
log = aml.event_log # 日志
info = aml.training_info # 时间5.5 Auto-Keras
1、简介
Auto-Keras是一种自动机器学习(AutoML)工具,旨在简化深度学习模型的构建和优化。它利用神经架构搜索(NAS)技术自动选择合适的模型结构和超参数,从而大大减少了人工调整的繁琐工作。
Auto-Keras通过智能搜索算法,自动搜索适合数据集的最佳模型结构和超参数,从而提供最佳的模型性能。它提供了简洁易用的接口,使得即使没有深入了解深度学习的用户也能够快速构建强大的深度学习模型。
Auto-Keras支持多种数据类型,包括传统的结构化数据、图像、文本和时间序列等不同类型的数据。它还提供了许多高级功能,如自动化模型选择、简洁的用户界面、支持多种数据类型等,使得即使没有专业知识的用户也能够快速构建强大的机器学习模型
安装Auto-Keras:
pip install autokeras对应python和TensorFlow的版本要求:Python >= 3.7 and TensorFlow >= 2.8.0.
官方学习地址:https://autokeras.com/
2、实战案例
import numpy as np
import tensorflow as tf
from tensorflow.keras.datasets import mnist
import autokeras as ak
# 导入数据集
(x_train, y_train), (x_test, y_test) = mnist.load_data()
print(x_train.shape) # (60000, 28, 28)
print(y_train.shape) # (60000,)
print(y_train[:3]) # array([7, 2, 1], dtype=uint8)
# 创建模型并训练
clf = ak.ImageClassifier(overwrite=True, max_trials=1)
clf.fit(x_train, y_train, epochs=10)
# 预测模型
predicted_y = clf.predict(x_test)
# 评估模型
clf.evaluate(x_test, y_test)使用验证数据集:
clf.fit(
x_train,
y_train,
validation_split=0.15, # 验证集比例
epochs=10,
)
# 手动切分验证集
split = 50000
x_val = x_train[split:]
y_val = y_train[split:]
x_train = x_train[:split]
y_train = y_train[:split]
clf.fit(
x_train,
y_train,
validation_data=(x_val, y_val),
epochs=10,
)自定义搜索空间:
input_node = ak.ImageInput()
output_node = ak.ImageBlock(
block_type = "resnet",
normalize=True, # 标准化
augment=False # 没有数据增强
)(input_node)
output_node = ak.Classification()(output_node)
clf = ak.AutoModel(inputs=input_node,
outputs=output_node,
overwrite=True,
max_trials=1)
clf.fit(x_train,y_train, epochs=10)5.6 AutoGluon
1、简介
AutoGluon是一个自动化机器学习框架,由AWS团队开发和维护。它可以自动调整超参数并选择最佳的深度学习模型来解决回归和分类问题。AutoGluon提供了一种简单易用的界面来控制自动机器学习流程,并且可以与其他常用的深度学习框架集成。
AutoGluon的原理是基于自动化机器学习的思想,它使用了一系列的算法和技术来实现自动化机器学习的过程。其中,AutoGluon使用了一种称为“神经架构搜索”的技术来自动化地选择最佳的模型架构。此外,AutoGluon还提供了一些实用的功能,例如自动数据增强、自动模型选择、自动调整学习率等。
Windows10系统下的安装:https://auto.gluon.ai/stable/install.html
conda create -n myenv pythnotallow=3.9 -y # 创建虚拟环境 指定python版本
conda activate myenv # 进入虚拟环境
pip install -U pip
pip install -U setuptools wheel
# 安装torch相关
pip install torch==1.13.1+cpu torchvisinotallow==0.14.1+cpu -f https://download.pytorch.org/whl/cpu/torch_stable.html
# 安装
pip install autogluon官网学习地址:https://auto.gluon.ai/stable/index.html
AutoGluon requires Python version 3.8, 3.9, or 3.10 and is available on Linux, MacOS, and Windows.
2、实战案例
import pandas as pd
import numpy as np
np.random.seed=42
import warnings
warnings.filterwarnings("ignore")
from autogluon.tabular import TabularDataset, TabularPredictor
# 读取在线数据
data_url = 'https://raw.githubusercontent.com/mli/ag-docs/main/knot_theory/'
train = TabularDataset(f'{data_url}train.csv')
# 数据基本信息
train.shape # (10000, 19)
train.columns
# 结果
Index(['Unnamed: 0', 'chern_simons', 'cusp_volume',
'hyperbolic_adjoint_torsion_degree', 'hyperbolic_torsion_degree',
'injectivity_radius', 'longitudinal_translation',
'meridinal_translation_imag', 'meridinal_translation_real',
'short_geodesic_imag_part', 'short_geodesic_real_part', 'Symmetry_0',
'Symmetry_D3', 'Symmetry_D4', 'Symmetry_D6', 'Symmetry_D8',
'Symmetry_Z/2 + Z/2', 'volume', 'signature'],
dtype='object')
# 目标变量
label = "signature"
train[label].describe()
# 模型训练
predictor = TabularPredictor(label=label).fit(train)
# 模型预测
test = TabularDataset(f"{data_url}test.csv")
pred = predictor.predict(test.drop(columns=label))
# 模型评估
predictor.evaluate(test, silent=True)
# 结果
{'accuracy': 0.9448,
'balanced_accuracy': 0.7445352845015228,
'mcc': 0.9323703476874563}
# 对比不同模型
predictor.leaderboard(test, silent=True)5.7 PyCaret
1、简介
PyCaret 是一个开源的、低代码的机器学习库,旨在简化机器学习工作流并提高工作效率。它是一个 Python 库,封装了多个流行的机器学习库和框架,如 scikit-learn、XGBoost、LightGBM、CatBoost、spaCy、Optuna、Hyperopt、Ray 等。
官方学习地址:https://pycaret.org/
基于清华源安装pycaret:
pip install pycaret -i https://pypi.tuna.tsinghua.edu.cn/simple
# 相关依赖安装
pip install pycaret[analysis]
pip install pycaret[models]
pip install pycaret[tuner]
pip install pycaret[mlops]
pip install pycaret[parallel]
pip install pycaret[test]
pip install pycaret[analysis,models]版本要求:
- Python 3.7, 3.8, 3.9, and 3.10
- Ubuntu 16.04 or later
- Windows 7 or later
2、实战案例
一个关于二分类问题的实战案例,使用内置的数据集
from pycaret.datasets import get_data
from pycaret.classification import *
data = get_data("diabetes")
# 查看数据基本信息
# 1-函数式API
s = setup(data, target="Class variable",session_id=123)
# 2-OOP API
from pycaret.classification import ClassificationExperiment
s = ClassificationExperiment()
s.setup(data, target="Class variable", session_id=123)
# 比较不同模型
# 函数式API
# best = compare_models()
# OOP-API
best = s.compare_models()
# 模型分析
# 函数式API
# evaluate_model(best)
# OOP-API
s.evaluate_model(best)
# 模型预测
# 函数式API
# predict_model(best)
# OOP-API
s.predict_model(best)模型的保存和加载使用:
# functional API
# save_model(best, 'my_first_pipeline')
# OOP API
s.save_model(best, 'my_first_pipeline')
# functional API
# loaded_model = load_model('my_first_pipeline')
# OOP API
loaded_model = s.load_model('my_first_pipeline')
print(loaded_model)5.8 MLBox
1、简介
MLBox是一个功能强大的自动化机器学习库,旨在为机器学习工程师和研究者提供一站式的机器学习解决方案。
MLBox提供了多种数据预处理、特征工程、模型选择和超参数优化等功能,可以帮助用户快速构建和评估各种机器学习模型。它还支持多种类型的任务,包括分类、回归、聚类和异常检测等。此外,MLBox还提供了一些额外的功能,如模型解释和模型部署等,可以帮助用户更好地理解和应用机器学习模型。它提供以下功能:
- 快速进行数据读取和分布式数据预处理/清洗/格式化。
- 高可靠性的特征选择和信息泄漏检测。
- 高维空间中精确超参数优化。
- 用于分类和回归的最先进的预测模型(深度学习,堆叠,LightGBM等)。
- 具有模型解释的预测。
官网学习地址:https://mlbox.readthedocs.io/en/latest/
python版本要求:_Python versions:_ 3.5 - 3.7. & 64-bit version only(32位的Windows系统不再支持)。
pip install mlbox基于源码的安装:
# linux 或者Macos
git clone git://github.com/AxeldeRomblay/mlbox
cd MLBox
python setup.py install2、实战案例
from mlbox.preprocessing import *
from mlbox.optimisation import *
from mlbox.prediction import *
paths = ["<file_1>.csv", "<file_2>.csv", ..., "<file_n>.csv"]
target_name = "<my_target>"
data = Reader(sep=",").train_test_split(paths, target_name)
data = Drift_thresholder().fit_transform(data)
# 评估模型
Optimiser().evaluate(None, data)
# 自定义搜索参数
space = {
'ne__numerical_strategy' : {"space" : [0, 'mean']},
'ce__strategy' : {"space" : ["label_encoding", "random_projection", "entity_embedding"]},
'fs__strategy' : {"space" : ["variance", "rf_feature_importance"]},
'fs__threshold': {"search" : "choice", "space" : [0.1, 0.2, 0.3]},
'est__strategy' : {"space" : ["LightGBM"]},
'est__max_depth' : {"search" : "choice", "space" : [5,6]},
'est__subsample' : {"search" : "uniform", "space" : [0.6,0.9]}
}
best = opt.optimise(space, data, max_evals = 5)
# 预测
Predictor().fit_predict(best, data)5.9 Auto-Pytorch
1、简介
Auto-PyTorch是一个自动机器学习的框架,它通过使用PyTorch实现神经网络体系架构的自动搜索。Auto-PyTorch可以根据数据集的特点自动选择最佳的神经网络架构,从而使得模型的性能达到最优。
Auto-PyTorch的算法会自动搜索神经网络的架构、超参数等,以寻找在特定数据集上表现最佳的模型。这种自动搜索可以通过GPU计算来加速,大大减少了人工调整模型参数和架构的繁琐工作。
要使用Auto-PyTorch,需要先安装PyTorch和Auto-PyTorch库。然后,可以通过编写简单的Python代码来定义训练和测试数据集,并调用Auto-PyTorch的API进行自动模型训练和测试。
GitHub官网地址:https://github.com/automl/Auto-PyTorch
安装:
pip install autoPyTorch
# 时序预测相关
pip install autoPyTorch[forecasting]手动安装:
# 创建虚拟环境
conda create -n auto-pytorch pythnotallow=3.8
conda activate auto-pytorch
conda install swig
python setup.py install2、实战案例
from autoPyTorch.api.tabular_classification import TabularClassificationTask
# 导入数据
import sklearn.model_selection
import sklearn.datasets
import sklearn.metrics
X, y = sklearn.datasets.load_digits(return_X_y=True)
X_train, X_test, y_train, y_test = sklearn.model_selection.train_test_split(X, y, random_state=1)
# 实例化分类模型
api = TabularClassificationTask()
# 自动化搜索
api.search(
X_train=X_train,
y_train=y_train,
X_test=X_test,
y_test=y_test,
optimize_metric='accuracy',
total_walltime_limit=300,
func_eval_time_limit_secs=50
)
# 计算准确率
y_pred = api.predict(X_test)
score = api.score(y_pred, y_test)
print("Accuracy score", score)六、基于算法的超参数调优6.1 基于算法的超参数调优
基于算法的超参数优化是指通过运行不同的算法,例如遗传算法、粒子群优化算法等,来自动调整超参数,以寻找最优的超参数组合。这种方法通过利用算法来搜索超参数空间,以找到最优的超参数组合。
基于算法的超参数优化通常需要设置一些参数,例如种群大小、迭代次数等,这些参数会影响优化的效果。在运行算法时,会根据一定的评估标准来评估不同超参数组合的效果,并逐渐搜索出最优的超参数组合。
6.2 常见用于超参数优化的算法
- Bayesian Optimization and HyperBand:一种超参数优化算法,结合了贝叶斯优化和HyperBand算法。BOHB的目标是在给定的预算内找到最优的超参数组合,使得机器学习模型在特定任务上的性能达到最佳。
- 遗传优化算法:遗传优化算法是一种通过模拟自然进化过程来搜索最优解的方法。它是一种全局优化方法,可以在一个较大的解空间内搜索最优解。
- 梯度优化算法:梯度优化算法是一种基于梯度下降的优化算法,用于求解复杂的优化问题。它通过迭代地调整参数,最小化损失函数,从而搜索最优解。在梯度下降算法中,每次迭代时,算法会根据当前梯度方向调整参数,更新参数的值。如动量梯度下降、Adam算法和L-BFGS算法等。
- 种群优化算法:种群优化算法是一种基于自然界生物进化原理的优化算法,它模拟了生物进化的过程,通过不断地迭代和优胜劣汰的过程,逐步寻找最优解。种群优化算法的核心思想是将待优化问题转化为一个适应度函数,然后通过不断地迭代和优胜劣汰的过程,逐步寻找最优解
6.3 Bayesian Optimization and HyperBand(BOHB)
1、简介
Bayesian Optimization and HyperBand混合了Hyperband算法和Bayesian优化。BOHB算法使用贝叶斯优化算法进行采样,并通过对超参数的组合进行评估来寻找最佳的超参数组合。它结合了全局和局部搜索的优势,能够快速找到最优的超参数组合,同时具有健壮性和可扩展性。
BOHB算法适用于深度学习任务,通过选择合适的超参数,可以显著提高模型的性能和准确性。它适用于不同的模型和数据集,可以轻松添加新的超参数和约束条件。
BOHB算法的步骤如下:
- 初始化:选择超参数的初始范围和分布,定义评估指标和评估次数。
- 运行贝叶斯优化算法:根据初始范围和分布,生成超参数组合,使用贝叶斯优化算法进行评估和选择。
- 根据HyperBand算法进行资源分配和模型选择:根据贝叶斯优化算法的评估结果,将模型分为若干等级,并根据等级分配不同的资源。
- 重复步骤2和3,直到达到预设的评估次数或预算。
- 输出最优的超参数组合:从所有评估结果中选择最优的超参数组合作为最终结果。
参考文献:https://www.automl.org/blog_bohb/https://neptune.ai/blog/hyperband-and-bohb-understanding-state-of-the-art-hyperparameter-optimization-algorithms
2、python实战案例
import numpy as np
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import Adam
from keras.losses import BinaryCrossentropy
from keras.metrics import Accuracy
from keras.utils import to_categorical
from sklearn.model_selection import train_test_split
from bandit import Bandit
# 加载数据集
data = np.loadtxt('data.csv', delimiter=',') # data数据集最后一个为预测目标变量,前面所有字段为特征变量
X = data[:, :-1]
y = to_categorical(data[:, -1])
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 定义模型
model = Sequential()
model.add(Dense(64, activatinotallow='relu', input_shape=(X_train.shape[1],)))
model.add(Dense(64, activatinotallow='relu'))
model.add(Dense(y_train.shape[1], activatinotallow='softmax'))
model.compile(optimizer=Adam(), loss=BinaryCrossentropy(), metrics=[Accuracy()])
# 定义BOHB优化器
def bohb(x):
model.set_weights(x)
history = model.fit(X_train, y_train, epochs=10, batch_size=32, validation_split=0.2)
loss, accuracy = history.history['val_loss'], history.history['val_accuracy']
return loss, accuracy
# 定义Bandit类
bandit = Bandit(bohb, n_iter=1000, n_restarts=10, noise=0.1)
# 进行优化
bandit.run()6.4 遗传优化算法(Genetic Algorithm)
1、什么是遗传算法?
遗传优化算法是一种通过模拟自然进化过程来搜索最优解的优化算法。
这种算法主要受到生物进化中自然选择、交叉(遗传信息重组)和突变过程的启发。遗传优化算法通常用于解决一些复杂的优化问题,如函数优化、组合优化、机器学习中的参数优化等。
https://cloud.tencent.com/developer/article/1425840
2、遗传算法的基本步骤:
- 初始化:首先,算法会随机生成一个种群,这个种群包含了可能的解决方案。
- 适应度评估:每个个体(即种群中的每一个解决方案)都有一个与其相对应的适应度值。这个适应度值表示该个体的优良程度,通常是目标函数值的一种度量。
- 选择:根据适应度值,选择种群中的一部分个体进行繁殖。高适应度的个体有更大的机会被选择。
- 交叉:被选中的个体通过交叉操作生成新的个体。这个过程模拟了生物进化中的基因重组。
- 突变:为了保持种群的多样性,会随机对某些个体进行突变操作,模拟了生物进化中的基因突变。
- 替换:用新生成的一批个体替换原来种群中的一部分个体,形成新的种群。
- 终止条件:如果满足终止条件(如达到最大迭代次数或最优适应度已经达到一定精度),则停止搜索,否则回到步骤2。
3、遗传算法的python实战
import numpy as np
# 目标函数
def f(x):
return x ** 2
# 遗传算法优化函数
def genetic_algorithm(n_pop, n_gen, lower_bound, upper_bound):
# 初始化种群
pop = np.random.uniform(lower_bound, upper_bound, n_pop)
# 计算适应度
fit = np.array([f(x) for x in pop])
# 进行遗传优化
for gen in range(n_gen):
# 选择
idx = np.random.choice(np.arange(n_pop), size=n_pop, replace=True, p=fit/fit.sum())
pop = pop[idx]
fit = fit[idx]
# 交叉
for i in range(0, n_pop, 2):
if np.random.rand() < 0.5:
pop[i], pop[i+1] = pop[i+1], pop[i]
pop[i] = (pop[i] + pop[i+1]) / 2.0
# 突变
for i in range(n_pop):
if np.random.rand() < 0.1:
pop[i] += np.random.normal(0, 0.5)
# 返回最优解
return pop[np.argmin(fit)]
# 参数设置
n_pop = 100 # 种群大小
n_gen = 100 # 迭代次数
lower_bound = -10 # 下界
upper_bound = 10 # 上界
# 进行遗传优化
best_x = genetic_algorithm(n_pop, n_gen, lower_bound, upper_bound)
print('最优解:x = %.3f, f(x) = %.3f' % (best_x, f(best_x)))- 定义了目标函数f(x) = x**2,然后实现了一个遗传算法优化函数
- 基于numpy库生成一个均匀分布的随机种群,并计算每个个体的适应度
- 在迭代过程中,使用轮盘赌选择、算术交叉和随机突变操作来生成新的种群。最后,返回适应度最小的个体,即最优解
6.5 基于梯度的优化Gradient Optimization Algorithm
1、什么是梯度优化?
基于梯度的优化是一种利用梯度信息进行优化的方法。其基本原理是利用目标函数的梯度信息来逐步迭代更新参数,以找到目标函数的最小值(或最大值)。
具体来说,梯度优化算法Gradient Optimization Algorithm通过计算目标函数的梯度,即函数在某一点的切线斜率,来决定参数更新的方向和步长。在每一次迭代中,算法根据梯度信息来更新参数,使得目标函数的值朝着梯度的反方向进行更新。通过这样的迭代过程,梯度优化算法可以逐步逼近目标函数的最小值点。
梯度优化算法还经常结合其他的优化技巧,如动量法、学习率退火等。
2、梯度优化算法的python实战
import numpy as np
# 加载数据集
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([0, 1, 1, 0])
# 参数初始化
theta = np.random.randn(2, 1)
alpha = 0.1 # 学习率
iters = 1000
# 梯度下降算法
for i in range(iters):
# 计算预测值和误差
y_pred = np.dot(X, theta) >= 0.5
error = y - y_pred
# 计算梯度
gradient = np.dot(X.T, error) / len(X) + alpha * theta
# 更新参数
theta -= gradient
# 输出结果
print('最优解:theta =', theta)6.6 基于种群的优化Population-based Optimization Algorithm
1、种群优化算法的原理种群优化算法Population-Based Optimization Algorithms(POAs)的原理基于群体智慧和群体进化规则,它通过模拟生物进化过程的算法来求解复杂优化问题。在种群优化算法中,每个个体都代表了一个可能的解,而整个种群则代表了所有可能的解。每个个体都有一个适应度值,表示其在优化问题中的优良程度。
算法的核心思想是将待优化问题转化为一个适应度函数,然后通过不断地迭代和优胜劣汰的过程,逐步寻找最优解。在每一次迭代中,种群中的每个个体都会根据其适应度值进行排序,然后根据一定的概率进行选择、交叉和变异,从而产生新的个体。这个过程会不断地重复,直到找到最优解或达到预设的迭代次数。
种群优化算法具有全局搜索能力强、对问题依赖少、鲁棒性强等优点,适用于解决复杂的非线性优化问题。常见的种群优化算法包括遗传算法、粒子群优化算法、蚁群算法等。2、种群优化算法的python实战
import numpy as np
# 适应度函数
def fitness(x):
return x ** 2
# 初始化种群
population_size = 100
gene_length = 10
population = np.random.randint(2, size=(population_size, 基因长度))
# 迭代进化
iters = 100 # 迭代次数
cross_entropy = 0.8 # 交叉概率
mutation_probability = 0.01 # 变异概率
for i in range(iters):
# 选择
selection_probability = fitness(population) / sum(fitness(population))
selected = np.random.choice(np.arange(population_size), size=population_size, p=selection_probability)
population = population[selected]
# 交叉
for j in range(population_size):
if np.random.rand() < cross_entropy:
pos = np.random.randint(gene_length)
population[j], population[j+1] = np.roll(population[j], pos), np.roll(population[j+1], pos)
# 变异
for j in range(population_size):
if np.random.rand() < mutation_probability:
pos = np.random.randint(gene_length)
population[j][pos] = 1 - population[j][pos]
# 计算适应度值并排序
fitness_value = np.array([fitness(x) for x in population])
fitness_value_index = np.argsort(fitness_value)[::-1]
population = population[fitness_value_index]
# 输出最优解
best_solution_index = np.argmax(fitness_value)
best_solution = population[best_solution_index]
print('最优解:',best_solution)