寻找存在的路径/寻找图中是否存在路径 C# 并查集
卡码网 107 与 力扣的1971 寻找图中是否存在路径 相似 感觉还是有点不熟悉得多练1
107. 寻找存在的路径
题目描述
给定一个包含 n 个节点的无向图中,节点编号从 1 到 n (含 1 和 n )。
你的任务是判断是否有一条从节点 source 出发到节点 destination 的路径存在。
输入描述
第一行包含两个正整数 N 和 M,N 代表节点的个数,M 代表边的个数。
后续 M 行,每行两个正整数 s 和 t,代表从节点 s 与节点 t 之间有一条边。
最后一行包含两个正整数,代表起始节点 source 和目标节点 destination。
输出描述
输出一个整数,代表是否存在从节点 source 到节点 destination 的路径。如果存在,输出 1;否则,输出 0。
输入示例
5 4
1 2
1 3
2 4
3 4
1 4输出示例
1提示信息
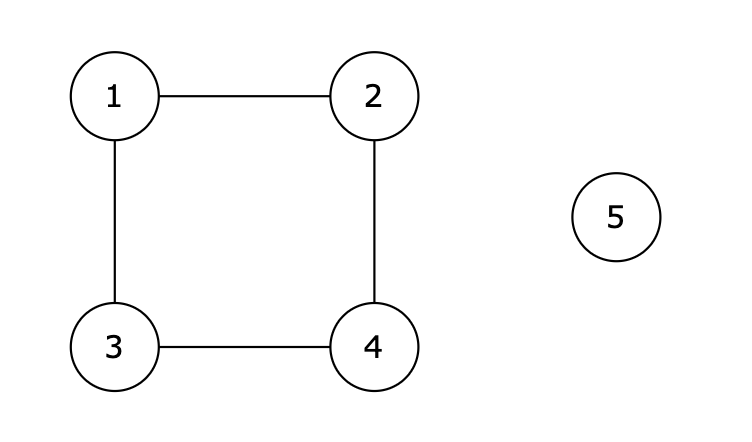
数据范围:
1 <= M, N <= 100。
思路:
并查集主要有三个功能:
- 寻找根节点,函数:find(int u),也就是判断这个节点的祖先节点是哪个
- 将两个节点接入到同一个集合,函数:join(int u, int v),将两个节点连在同一个根节点上
- 判断两个节点是否在同一个集合,函数:isSame(int u, int v),就是判断两个节点是不是同一个根节点
题目中各个点是双向图链接,那么判断 一个顶点到另一个顶点有没有有效路径其实就是看这两个顶点是否在同一个集合里。
如何算是同一个集合呢,有边连在一起,就算是一个集合。
此时我们就可以直接套用并查集模板。
使用 join(int u, int v)将每条边加入到并查集。
最后 isSame(int u, int v) 判断是否是同一个根 就可以了。
需要注意的点: C#中的类与构造函数的使用 本体使用构造函数主要是因为 初始化 UnionFind 类的实例,并设置并查集所需的数据结构。
构造函数的作用是:
- 初始化并查集的核心数据结构
father数组。 - 保证每个节点最初是自己独立的集合的根节点。
- 为后续的合并操作(
Join)和查找操作(find)提供正确的初始状态。
作用:1. 初始化 father 数组 2. 初始化并查集结构


using System;
public class Program {
public static void Main(string[] args) {
int N, M;
string[] firstLine = Console.ReadLine().Split();
N = int.Parse(firstLine[0]);
M = int.Parse(firstLine[1]);
Unifind un = new Unifind(N + 1); // 注意:N + 1 是因为索引从 1 开始
for (int i = 0; i < M; ++i) { //不断输入 初始化完整个 father 数组
string[] edge = Console.ReadLine().Split();
un.Join(int.Parse(edge[0]), int.Parse(edge[1]));
}
//最后一行代表存在 节点sources到目标点 的路径
string[] query = Console.ReadLine().Split();
if (un.IsSame(int.Parse(query[0]), int.Parse(query[1]))) {
Console.WriteLine("1");
} else {
Console.WriteLine("0");
}
}
}
public class Unifind {
private int[] father;
public Unifind(int N) {
father = new int[N];
for (int i = 0; i < N; ++i) {
father[i] = i; // 每个节点的父节点初始化为自己
}
}
// 查找操作(带路径压缩)
public int Find(int n) {
if (n != father[n]) {
father[n] = Find(father[n]); // 路径压缩
}
return father[n];
}
// 合并操作
public void Join(int n, int m) {
int rootN = Find(n);
int rootM = Find(m);
if (rootN != rootM) {
father[rootM] = rootN; // 将 m 的根节点指向 n 的根节点
}
}
// 判断两个节点是否属于同一个集合
public bool IsSame(int n, int m) {
return Find(n) == Find(m);
}
}
