四焦距聚焦型光场计算成像系统的设计
摘要: 光场相机是一种在图像传感器前增加微透镜阵列的新型相机结构,除了记录不同位置下光的强度及颜色外,也记录不同位置下光线的方向信息,从而能够计算目标场景的深度图和高阶相位图。该技术由于景深和分辨率相互制约,获得大景深时分辨率会降低。分析了其结构特点并推导了景深和分辨率的关系,并就选定的设计参数绘制了变化曲线。在此基础上,提出了一种新型光场相机的设计方法,该结构基于具有四类焦距的微透镜阵列,可获得超大景深,同时将分辨率的下降程度控制在可接受范围。仿真结果表明:相对于三类焦距微透镜阵列,所设计的四类焦距微透镜阵列景深可提高三倍,而分辨率达到普通相机的18.9%。
关键词: 光场相机;景深;有效分辨率比率;多焦距;微透镜阵列
0 引言
在新型成像技术领域,基于光场相机的计算成像将日新月异的计算能力和逐渐成熟的微阵列光学结构加工能力结合在一起,形成了全新的光场重建方式,成为近年来的研究热点。根据光场理论,如果能够获取物点在不同方向上的强度分布就能准确解算出全视场的深度图谱,而光场相机通过在传统相机的主透镜和图像传感器之间加装微透镜阵列(MicrolensArray,MLA),实现了这一目标[1]。
光场相机可分为非聚焦型和聚焦型两种:第一种非聚焦结构微透镜阵列位于主透镜的焦面,原则上景深无限大,但是成像分辨率很低,仅仅等于微透镜数目,这是其重要缺陷;第二种聚焦型结构成像元件离开焦平面一定距离,等效于对主镜头的成像进行二次分孔径成像,分辨率大大提高,但是付出的代价是景深急剧缩短,依旧无法摆脱分辨率和景深之间的相互制约。
文中详细分析了光场相机景深与分辨率之间的关系,在此基础上提出了一种四焦距微透镜阵列的聚焦型光场相机,基于不同深度为目标光场匹配不同焦距类型的微透镜阵列,使四段景深衔接,极大地扩展了系统的景深范围,达到三焦距微透镜阵列的光场相机景深的6倍,同时控制成像区域完全覆盖视场区域,使分辨率仅下降到普通相机的18.9%,一定程度上解决了光场相机的技术瓶颈。
1 背景
1.1传统相机
在介绍光场相机的景深之前,首先分析一下传统相机的景深。
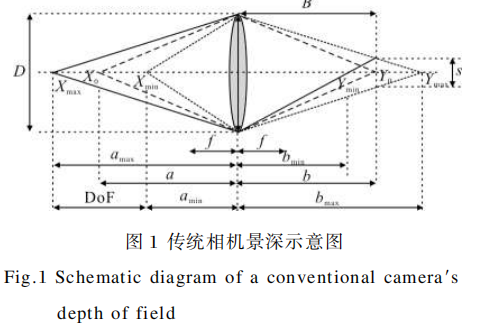
如图1所示,理想情况下透镜左方X0点发出的所有光线经过透镜后都将汇聚到透镜右方Y0处,它们之间的关系由薄透镜方程表示[2]:

式中:f为透镜焦距。如果在距离透镜B的Y0处放置传感器,那么在光轴上比X0近或远的点发出的所有光线经过透镜后将在传感器上呈扩散圆,这意味着为了确保图像的锐利程度,使图像看起来清晰,传统相机只能将物空间一定深度范围最佳成像到像空间。这一深度范围称之为景深(Depth of Field,DoF)。
实际上由于衍射效应的作用,点光源经过透镜后并不能汇聚到一个点,而是具有一定的强度分布,称之为艾里斑[3]。描述其大小的一个近似公式是:

式中:sλ为艾里斑半径;入为光波长;D为透镜直径;B为透镜到传感器的距离。由瑞利准则可知,如果拍摄的两个物体之间的距离足够小,以至于相机传感器上的艾里斑开始重叠,将无法清晰分辨物体。当两个艾里斑变得比其宽度的一半更近时,它们就不能再分辨了。定义F#=B/D为工作F数[4],当B增大时,艾里斑半径也随之增大。因此像元密度决定了成像系统的分辨率,艾里斑限制了能够达到的极限分辨率。
透镜左方X0点发出的所有光线经过透镜后都将汇聚到透镜右方Y0处,而透镜左Xmin~Xmax之间的点发出的光线将在距离透镜B处的传感器上扩散成一定范围,因此s表示扩散圆直径。由图1中几何关系易得:

式中:正负号分别对应着B>b和B<b的情况。一维情况下,有效分辨率Re和Rt总分辨率定义为:
![]()
式中:LCCD为传感器长度;p为每个像元尺寸。实际上有效分辨率比率(Effective Resolution Ratio,ERR)是评价相机设计更有说服力的参数[5],它定义为:
![]()
选取一组参数,透镜直径D=0.3mm,焦距f=1.8mm,传感器像元尺寸p=5.5μm,光波长入=550nm,分别在B=2.4mm和B=4mm时绘制有效分辨率比率ERR随着物距a的变化示意图,如图2所示
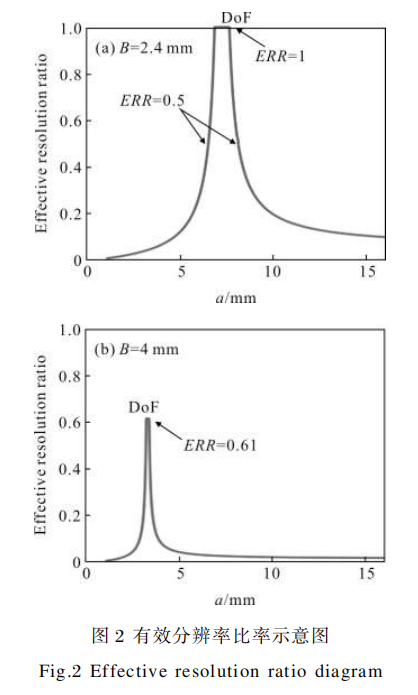
从图中可以看到,B值会影响景深的范围和有效分辨率比率的大小。图2(a)中,B值较小,工作F数较小,此时衍射效应不明显,结合公式(4)可知此时像元尺寸p起主导作用,p较小时,即像素密时,景深小;p较大时像素疏,景深大。图2(b)中,B值较大,工作F数较大,此时衍射效应使成像系统的ERR整体下降,使峰值小于1。从图(a)中还可以看到,ERR=0.5时的景深比ERR=1时大,即通过降低有效分辨率比率,可以使景深得到扩展。
1.2光场相机
传统相机中传感器上每一个像素捕获的子图像都是对入射到该点的所有光线强度的积分[6]通过在传统相机的主透镜和传感器之间插入微透镜阵列,可以分别捕获每一细束光线,因此传感器上不同的像素代表着不同角度范围的入射光线,构成光场相机。
在第I代光场相机中,微透镜阵列放置在主透镜焦平面处,计算成像后获得图像的分辨率和微透镜数量相等[1],如图3(a)所示第II代光场相机是将微透镜阵列放置在稍微不同的地方,主透镜成像到微透镜阵列前(成实像,如图3(b)所示)或后(成虚像),然后微透镜阵列对主透镜所成的像进行成像,即将微透镜阵列看作是微相机阵列,每个微相机对从主透镜过来的光线成聚焦的微图像,因此第II代光场相机常常称为聚焦光场相机或者全光2.0。通过这一改进,使得微透镜可以捕获密集的位置信息,而不是捕获密集的方向信息,以牺牲方向分辨率为代价显著提高空间分辨率,使空间分辨率远高于微透镜数量[7]。
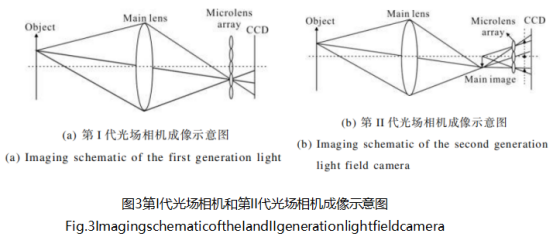
第II代光场相机使用微透镜阵列将主镜头的像二次成像到CCD上,即它可以对微透镜前面的特定平面的4D辐射进行采样。景深决定了后期通过计算能够清晰成像的范围,因此微透镜阵列的景深需要尽可能大。小孔径的微透镜可实现大景深,但这会导致工作F数较大和通光率较低,工作F数大时衍射效应会模糊图像。
为了解决大孔径和大景深不能够同时获得这一矛盾,Todor Georgiev 等人提出了基于具有不同焦距的微透镜阵列的传感器设计[6],以便它们聚焦在两个或更多个不同的平面上,如图4所示。
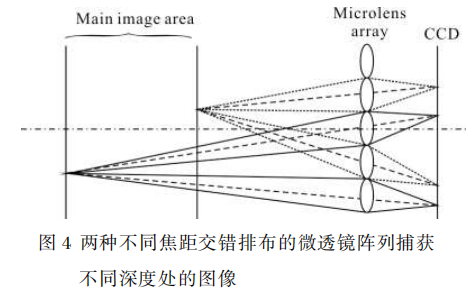
Christian Perwass等人在Raytrix工业级相机中采用三焦距微透镜阵列,通过选择合适的焦距可以使不同焦距的微透镜景深基本上相接,增大了整个光场相机的景深[5]。
2 新型四焦距微透镜阵列设计
基于以上分析,笔者提出了一种新型多焦距光场相机,基于具有四焦距的微透镜阵列,采用六边形周期性紧密排布方式,理论分析表明,通过选择合适的微透镜焦距,可以扩展景深,对物空间中任意深度处,通过计算成像可以获得接近理论极限分辨率的图像。
2.1虚深度
图3(b)中,主透镜将物空间成像到微透镜阵列前,这样的结构称为成实像的光场相机,参考文献[4]中称为开普勒结构;相应的,主透镜将物空间成像到微透镜阵列后,称为成虚像的光场相机,称为伽利略结构。不失一般性,笔者仅讨论成虚像的光场相机,即伽利略结构的光场相机。对于成实像的光场相机的讨论也是类似的。
参考文献[5]中一般将主透镜所成的像到微透镜的轴向距离a与微透镜阵列到传感器的距离B之比称为虚深度,即v=a/B。虚深度描述了主透镜像点与微透镜阵列和CCD的相对位置关系,即对于成虚像的光场相机(v是负数),|v|越小表示在越少的微透镜下成像。考虑一维情况下,例如,虚深度为-1时,意味着该平面内的主透镜所成的每一个像点都至少能被一个微透镜二次成像,即v=-1时实现了对主透镜所成像的全覆盖。为了能够实现深度估计,主透镜所成的像点至少要被两个微透镜二次成像,即虚深度从-2开始时,可进行深度估计。
2.2排布方式
图5(a)、(b)是微透镜阵列两种典型的排布方式。采用六边形排布方式相比于采用正交排布方式可以将填充率从(约0.79)提高到这提高了传感器上的光能利用率。
图5也可看做微透镜阵列在虚深度|v|=1处的投影截面。如前所述,一维情况下|v|=1意味着该平面内每一个主透镜所成像点都只能被一个微透镜成像,即要实现对整个主透镜所成像全覆盖,需要|v|≥1。
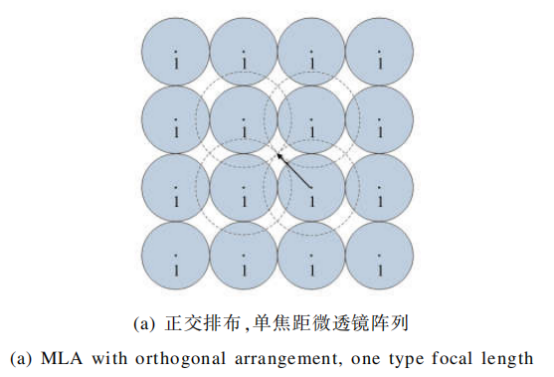
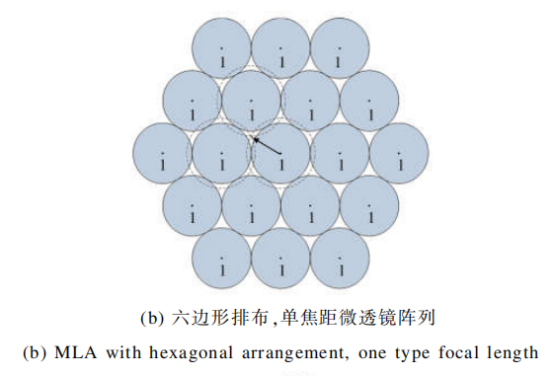
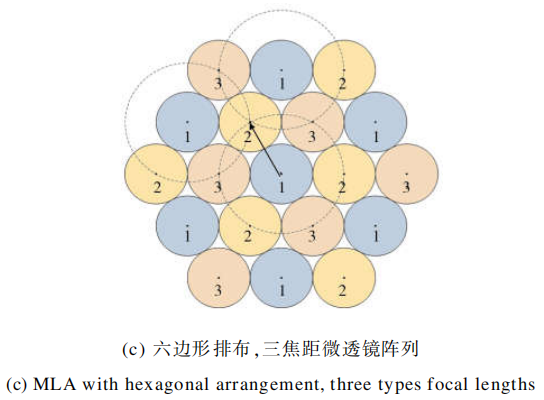
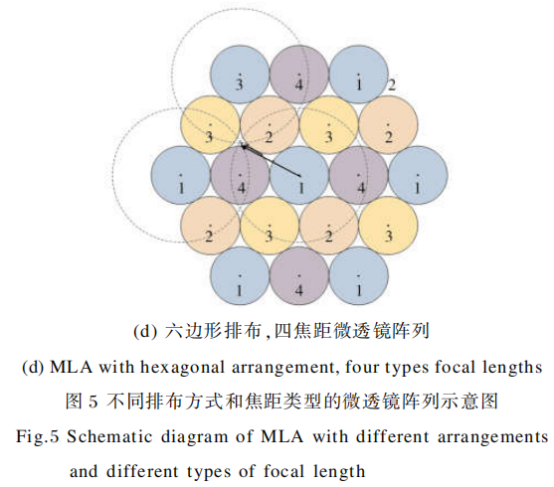
二维情况则不同,|v|=1时会在投影面留下间隙,导致微透镜对主透镜所成像点采样有遗漏,共轭到真实的物空间时信息不全。当虚深度增大时,每个微透镜的投影圆都将线性增大。图中虚线圆表示同一类焦距微透镜实现主透镜像全覆盖时的最小投影圆,箭头表示最小投影圆半径。由几何关系可得实现主透镜的像全覆盖时的虚深度范围,如表1所示。

从表1中可以看出:采用六边形排布相比于正交排布可以以较低的虚深度实现对主透镜像的全覆盖,在后面的分析会指出随着虚深度的增大,ERR会下降,相同情况下六边形排布获得的图像分辨率更高,这是采用六边形排列的另一个优势。在六边形排布的情况下,考虑三种不同类型焦距,如图5(b)~(d)所示,在相同的排列方式下,焦距类型增多时要实现对主透镜像的全覆盖,虚深度下限随之增大,即理论最高分辨率会下降,这是焦距类型增多时的一个劣势。
2.3 有效分辨率比率
仍然考虑一维情况,虚深度增大时,主透镜所成像点将会在更多微透镜下成像,若不考虑景深的影响因素,光场相机将达到理论极限ERR:
ERR=1/|v| (6)
由公式(6)可得到虚深度v与理论极限ERR的关系,如图6所示。
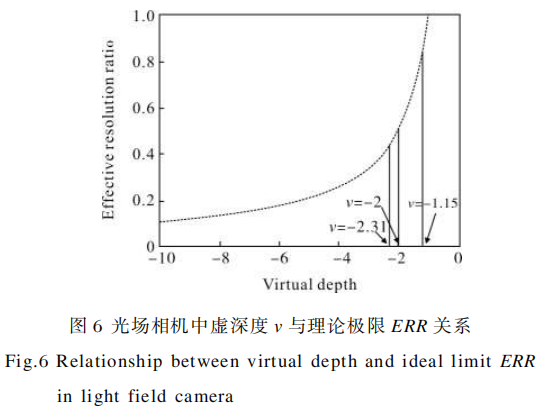
图中点画线表示虚深度v与理论极限ERR关系。易知随着|v|增大,ERR下降。图中标注箭头的三条虚线分别是单焦距、三焦距、四焦距微透镜阵列六边形排列时的虚深度起始值。通过选取合适的焦距,可以使实际光场相机的ERR在局部虚深度处达到理论极限。结合公式(5),得到一维情况下光场相机的有效分辨率比率:
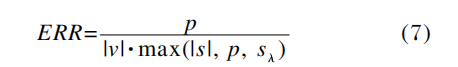
式中:|v|≥1,二维情况下的有效分辨率比率近似等于一维情况下有效分辨率比率的平方。前面已经分析过,工作F数增大时,衍射效应使成像系统的有效分辨率比率整体下降。考虑模糊圆半径不大于像元尺寸,即s入≤p,由公式(2)可得:

通常取光波长入=550nm,由该式可知当像元尺寸p较小时,工作F数也要相应减小,否则会造成像素浪费。当工作F数减小时,景深会变短。为了获得较大的景深,在设计光场相机参数时希望工作F数能够尽量大。
选定一组光场相机参数,像元尺寸p=5.5μm,工作F数F#=8,微透镜直径D=0.22mm。由工作F数的定义,可以得到微透镜到传感器的距离B=1.76mm。由公式(8)可知这组参数满足工作F数要求。对于单焦距微透镜阵列,虚深度v=-1.15时对主透镜像全覆盖,对于三焦距微透镜阵列,虚深度v=-2时对主透镜像全覆盖,合理选择三类焦距,使景深相接,如图7所示。
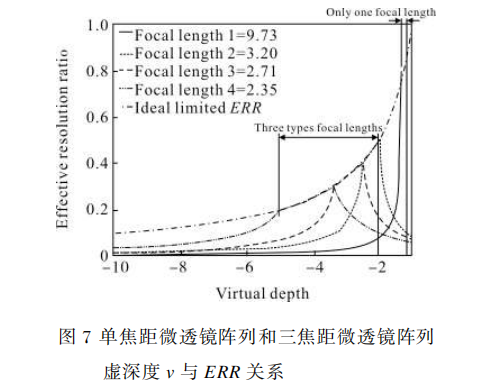
从图7中可以直观地看到采用多焦距微透镜阵列替代单焦距微透镜阵列的优势。对于单焦距微透镜阵列,虚深度范围短,ERR曲线高,即景深短、分辨率高。当采用三焦距微透镜阵列时,虚深度范围宽,ERR曲线下移,即以牺牲分辨率为代价获得景深的扩展。
从图7中还可以看到,采用三焦距的微透镜阵列在虚深度|v|>1时,ERR曲线快速下降,低于理想曲线。为了获得更大的景深,同时使分辨率下降程度可接受,笔者提出了一种四焦距微透镜阵列。与三焦距微透镜阵列设计相类似,四焦距微透镜阵列采用六边形周期性紧密排布方式,虚深度v=-2.31时对主透镜像全覆盖,选择合适的焦距,使不同焦距的微透镜景深相接,如图8所示。
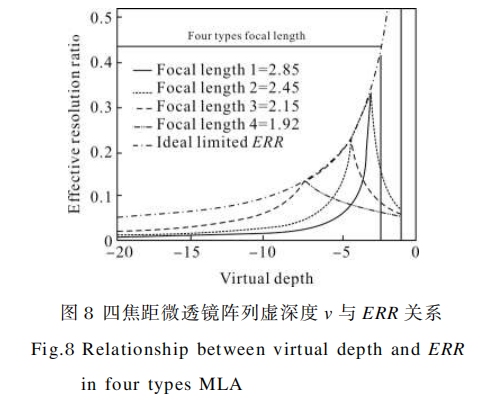
笔者认为,ERR下降到0.05时是可以接受的值,从图中可以看到,通过选择合适的微透镜焦距,四焦距微透镜阵列可将虚深度扩展到20,相比单焦距微透镜阵列和三焦距微透镜阵列,在虚深度大时,分辨率更高。取ERR≥0.05为虚深度范围,在前面选定的光场相机参数下,可得表2。
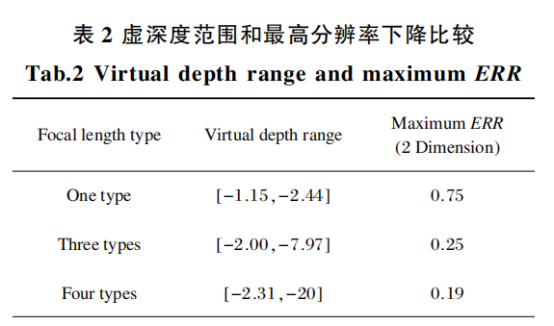
从表中可以看到,三焦距微透镜阵列峰值ERR为1/4,而四焦距微透镜阵列峰值ERR约为1/5,采用四焦距微透镜阵列相对于单焦距和三焦距微透镜阵列,虚深度分别扩展了13.7、3倍,即虚深度的扩展是以牺牲最高分辨率为代价的。
3 结论
文中分析并提出了一种新型四焦距微透镜阵列。在传统相机和光场相机研究的基础上,通过分析景深和分辨率制约的关系,提出了新型微透镜阵列设计方法。相比于Raytrix工业级相机采用三焦距微透镜阵列,该设计可以将景深扩展三倍。通过该设计,不同焦距的微透镜的视场深度将覆盖传感器前面的整个空间,给定场景中任意一点,至少有一组微透镜将会清晰地聚焦,为扩展光场相机的景深提供了一种切实可行的方案。
文章来源:《红外与激光工程》
作者:王佳华,杜少军,张烜喆,李俊,王 彦,刘青松(国防科技大学 前沿交叉学科学院,湖南 长沙 410073)
声明:转载此文目的在于传递更多信息,仅供读者学习、交流之目的。文章版权归原作者所有,如有侵权,请联系删除。
