基于的图的异常检测算法OddBall

OddBall异常检测算法出自2010年的论文《OddBall: Spotting Anomalies in Weighted Graphs》，它是一个在加权图(weighted graph)上检测异常点的算法，基本思路为计算每一个点的一度邻域特征，然后在整个图上用这些特征拟合出一个函数，再根据拟合出来的参数计算每个点的异常分数，所以它可以用于无监督场景。

OddBall检测的异常情况如论文图1所示的四种情况：

• Near-cliques: 节点的邻居之间紧密联系，典型的情况可能是恐怖组织或者成员之间非常活跃的讨论组。（clique是图里的团，一个clique里的节点两两之间都有一条边）
• Near-starts: 星状结构，节点的邻居之间几乎没有什么联系，典型的情况有中介、电话销售、机器营销号码等。
• Heavy vicinities: 节点的邻居个数固定，但是这些边对应的权重之和异常地大。比如在一个电话网络里，一个节点只有有限的n个联系人，但是总的呼叫次数非常大，与n不成比例，说明可能存在强制重拨的异常设备，或者在伪造通话记录等。
• Dominant heavy links： 图里有某一条边的权重占主导地位。比如在一个电话网络里，一个stalker可能会在短时间内不停地给某个联系人打非常多的电话。

论文借用社交网络分析(social network analysis, SNA)的术语，将图中每一个节点称为’ego’，将一个节点与其1-step邻居节点组成的网络称为egonet。一个节点k-step邻居即从节点出发k步能到达的邻居节点集合，这些邻居节点之间组成了一个子图。关于k的选择，论文推荐使用k=1，有之前的论文表明现实中的图有比较小的直径，论文实验时也发现k>1没有提供更多的信息。（不过在想随着这些年社交媒体和移动互联网的快速发展，现在的数据来说k>1在一些场景下是可能提供更多信息的）

对一个egonet，选择什么特征来描述它呢？比如很容易能想到的特征有：节点个数、边个数、特征值、三角形个数、度为1的邻居的个数等。论文经过试验，最终选择了如下4个特征来刻画egonet:

• $N_i$： ego i对应的邻居个数，即节点i的度。
• $E_i$：egonet i包含的边的数目。
• $W_i$：egonet i的总权重。
• ${\lambda }_{w,i}$：egonet i的带权邻接矩阵的主要特征值。

接着，论文用这4个特征组成特征对来检测前面提到的几种异常：

• $E$ vs $N$： 用来检测near-cliques和near-stars。
• $W$ vs $E$： 用来检测Heavy Vicinity。
• ${\lambda }_w$ vs $W$： 用来检测Dominant heavy links。

在检测异常时，自然地就会问一个正常的邻居节点是什么样子的呢？基于上述特征对，Oddball作者们总结了下文的一些模式。对于一个给定的图$\mathcal{G}$，其节点i $i\in \mathcal{V}(\mathcal{G})$， 节点的i的egonet记为${\mathcal{G}}_i$。（注：如果只想知道Oddball是如何计算异常分数的，下面这些模式可先略过不看，不过这些模式有助于理解Oddball的异常分数计算思路）

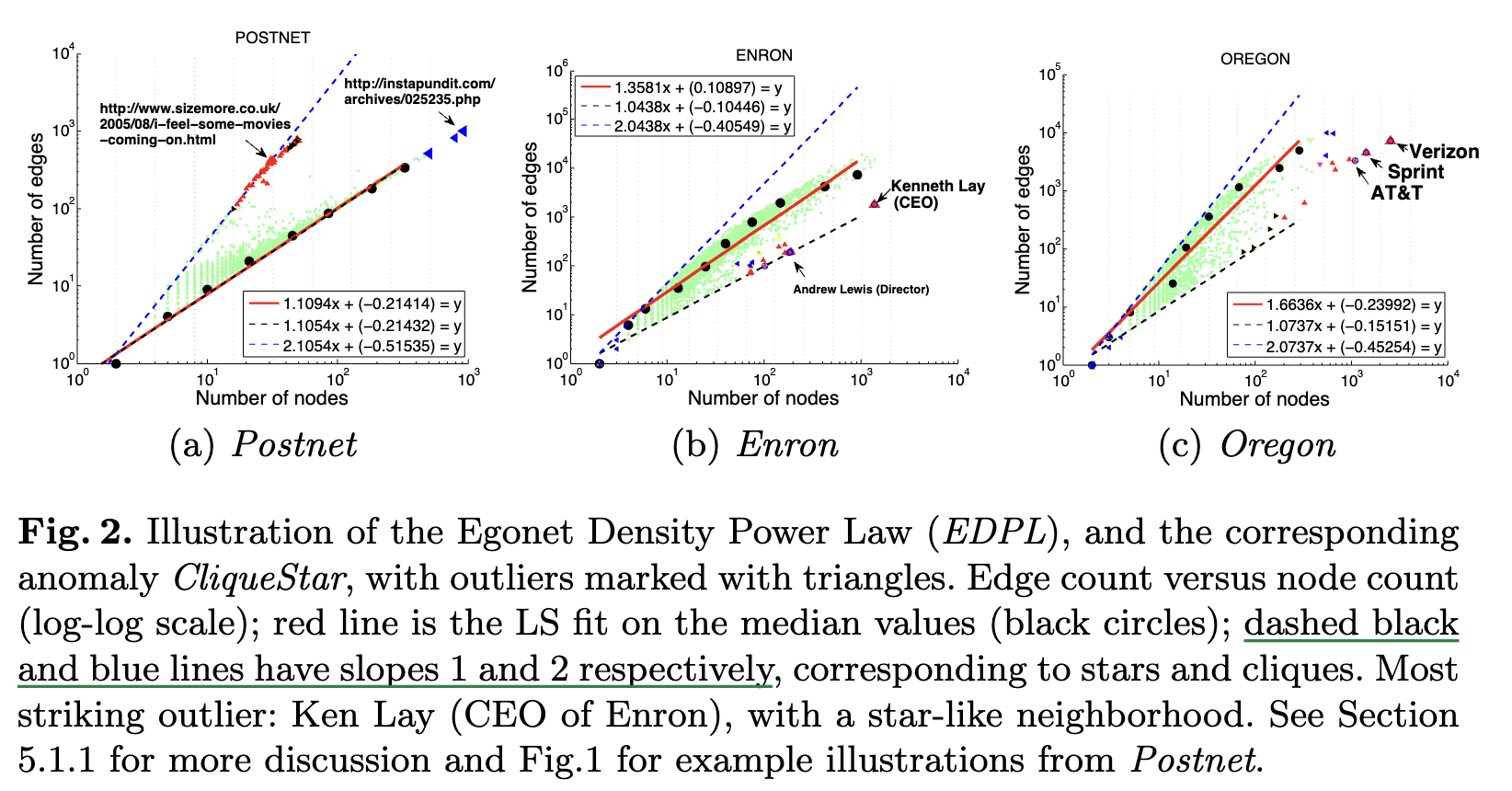
观察1 (EDPL: Egonet Density Power Law) ： ${\mathcal{G}}_i$的邻居个数$N_i$和边的条数$E_i$满足幂率:
$$E_i\propto N_i^{\alpha },1\le \alpha \le 2$$
在论文实验时的指数$\alpha$大小为1.10到1.66。论文图2示意了这个观察（图是在对数维度画的），当斜率为2时，代表图为一个clique，而斜率为1，代表图为star。

观察2 (EWPL: Egonet Weight Power Law)：${\mathcal{G}}_i$的总权重$W_i$和边的条数$E_i$满足幂率:
$$W_i\propto E_i^{\beta },\beta \ge 1$$

论文图3展示了数据集的EWPL示意，$\beta$最大达到了1.29， $\beta >1$表明随着边的增加，权重之和的增加有超线性的增长。

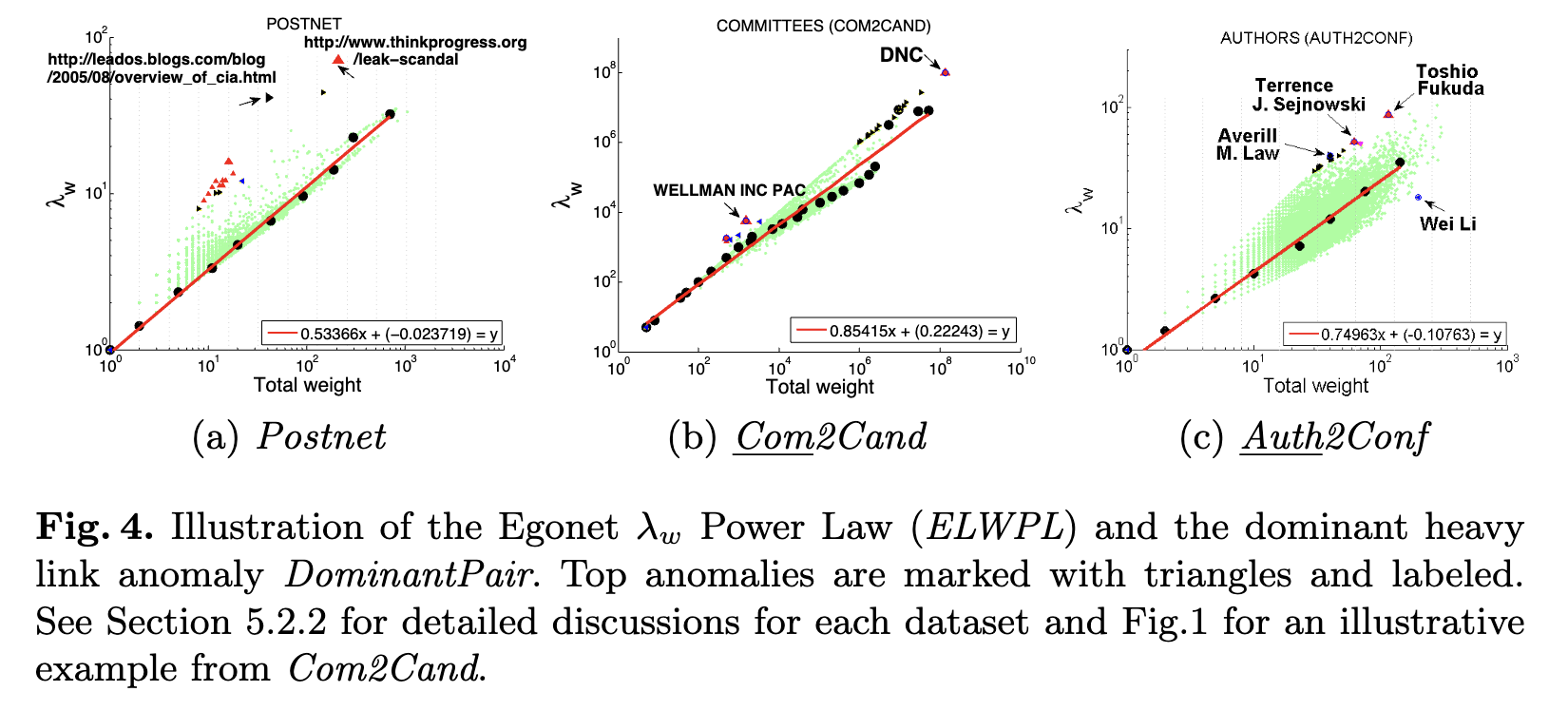
观察3 (ELWPL: Egonet ${\lambda }_w$ Power Law)：${\mathcal{G}}_i$的带权邻接矩阵的主要特征值${\lambda }_{w,i}$和总权重$W_i$满足幂率:
$${\lambda }_{w,i}\propto W_i^{\gamma },0.5\le \gamma \le 1$$

论文图4示意了数据集的ELWPL，实验中$\lambda$范围为0.53至0.98。$\gamma =0.5$表示均匀的权重分布，$\gamma \sim 1$表示在egonet中有显著权重边。 $\gamma =1$表示egonet只有一条边。

观察4 (ERPL: Egonet Rank Power Law)：${\mathcal{G}}_i$中的边j的排序$R_{i,j}$和权重$W_{i,j}$满足幂率:
$$W_{i,j}\propto R_{i,j}^{\theta },\theta \le 0$$

$R_{i,j}$是边j按照边权重排序之后的排名。ERPL表明在egonet中边的权重分布是倾斜的。这个是符合直觉的，比如在一个朋友网络中，一个人会有许多不亲近的朋友，但只有少数几个亲近的朋友。接着论文证明了如果ERPL成立，则EWPL也成立。

有了前面这些铺垫，现在让我们看看Oddball是如何计算异常分数的。对于前面提到的特征对（根据检测异常类型选择特征对），设节点i的对应的y值记为$y_i$，对应的x值为$x_i$，假设对于数据集可以拟合得到一个幂率方程$y=C{x}^{\theta }$，定义节点i的异常分数为：

$$\text{out-line}(i)=\frac{\max (y_i,C{x}^{\theta })}{\min (y_i,C{x}^{\theta })}\ast \log (|y_i-C{x}^{\theta }|+1)$$

直观上，Oddball的异常分数度量“偏离拟合曲线的距离”，当真实值$y_i$与期望值$C{x}^{\theta }$相等时，异常分数为最小值0。

作者发现Oddball有时候检测不到一些异常点，比如在图2(a)中的左三角标记的点，它们与其他点隔的很远但是几乎就在拟合线上。所以作者提出将Oddball异常分数与基于密度的异常检测方法一起结合使用。在论文中，使用的基于密度的异常检测方法是LOF方法，将Oddball分数和LOF分数进行归一化后(通过除以最大值的方式)求和得到最终的异常分数，即$\text{out-score}(i)=\text{out-line}(i)+\text{out-lof}(i)$。

实践经验：1. 在计算一个egonet里的边的数目时，可以通过计算egonet里三角形个数和其度之和来得到。因为现有的工具比如Spark GraphX里已经有三角形个数和度计算的现成接口。2. 计算LOF时，在图里怎么算距离呢? 把选定的特征对数据作为LOF的特征再计算距离。

参考资料

1. OddBall: Spotting Anomalies in Weighted Graphs
2. 实现： oddball 作者主页上的matlab代码, github上的python实现：1, 2