算法笔记：前缀和

1. 前缀和的定义

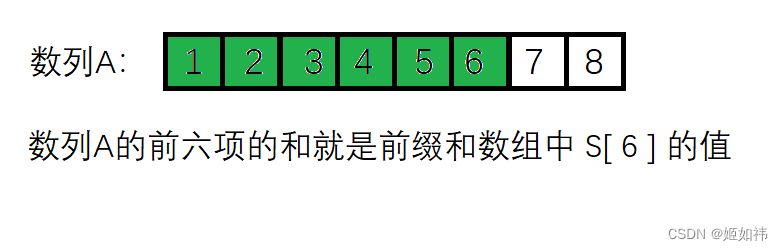
对于一个给定的数列A，他的前缀和数中 S 中 S[ i ] 表示从第一个元素到第 i 个元素的总和。

如下图：绿色区域的和就是前缀和数组中的 S [ 6 ]。

2. 一维前缀和

2.1 计算公式

前缀和数组的每一项是可以通过原序列以递推的方式推出来的，递推公式就是：S[ i ] = S[ i - 1 ] + A[ i ]。S[ i - 1 ] 表示前 i - 1 个元素的和，在这基础上加上 A[ i ]，就得到了前 i 个元素的和 S [ i ]。

2.2 用途

一维前缀和的主要用途：求一个序列中某一段区间中所有元素的和。有如下例子：

有一个长度为 n 的整数序列。

接下来输入 m 个询问，每个询问输入一对 l，r。

对于每个询问，输出原序列中第 l 个数到第 r 个数的和。

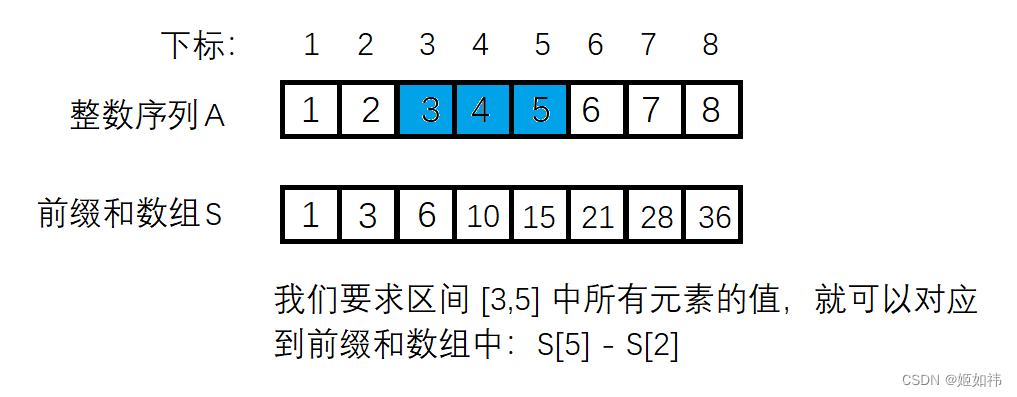
这边是对前缀和的应用，如果用常规的方法：从 l 到 r 遍历一遍，则需要O(N)的时间复杂度。但是有前缀和数组的话，我们可以直接利用公式：sum = S[ r ] - S[ l - 1 ]，其中sum是区间中元素的总和，l 和 r 就是区间的边界。下图可帮助理解这个公式。

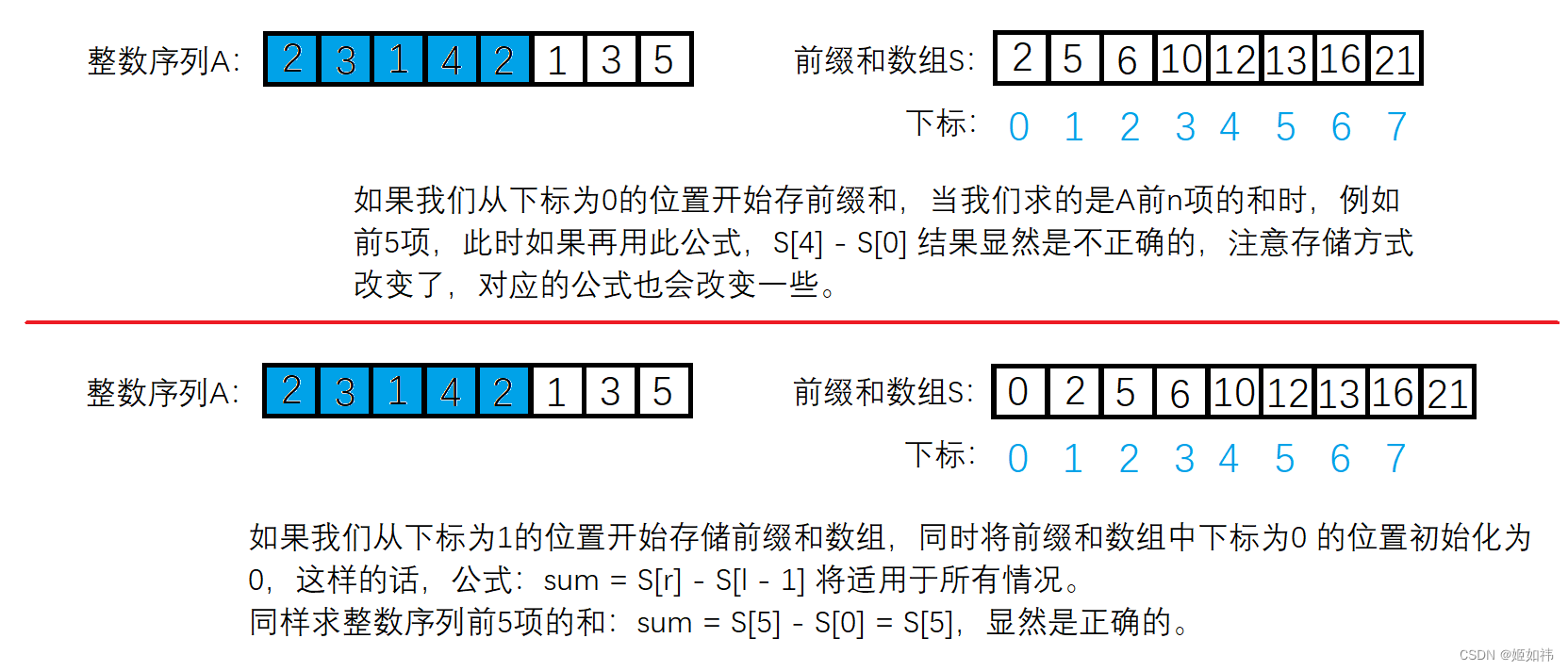
当我们要求的是序列 A 的前 n 个数之和时，如果我们是从下标为 0 的位置开始存储前缀和数组，此公式：sum = S[ r ] - S[ l - 1 ] 显然就无法使用了，为了是这个公式适用于所有情况，我们将从下标为 1 的位置开始存储前缀和，并且将下标为 0 的位置初始化为 0。

3. 步骤与题解

首先就是要构造一个和目标数组等长的一个前缀和数组pre[]，前缀和数组公式为pre[i]=pre[i-1]+nums[i];也就是前一项的和+当前位置的值就是当前位置的前缀和。

那么假设我们相求[j,i]这个范围内的子数组就为pre[i]-pre[j-1]=k;移项就可以知道目标为k的符合的需要满足

pre[j-1]=pre[i]-k; 也就是当前项的前缀和减去目标值pre-traget。

所以我们考虑以 i 结尾的和为 k 的连续子数组个数时只要统计有多少个前缀和为 pre[i]−k 的 pre[j] 即可，那么就可以通过一个map来记录，只需要记录pre[i]出现的次数即可。

模板步骤：

int pre=0; //前缀和
int traget=0; //目标值
HashMap<Integer,Integer> map=new HashMap<Integer,Integer>;
map.put(0,1); //注意前缀和数组或者map一定要初始化 (0,1)
for(int i=0;i<nums.length;i++){
    pre+=nums[i]; //当前前缀和
    map.getOrDefault(pre-traget,0); //获取符合目标的值
    map.put(pre,map.getOrDefault(pre,0)+1);//然后将当前的前缀和加入到结果中
}

 代码：

class Solution {
    Map<Long,Integer> map=new HashMap<>(); //保存前缀和结果
    int target=0; //结果
    public int pathSum(TreeNode root, int targetSum) {
         //前缀和+递归
         target=targetSum; //目标结果
         map.put(0L,1); //前缀和为0的个数至少为一个
         return   dfs(root,0L);

     }

    public int dfs(TreeNode node,Long count){ //节点 count为当前节点需要达到的目标数
            if(node==null){
                return 0;
            }
            count=count+node.val; // 当前前缀树的值：10
            int result=0;
            result=map.getOrDefault(count-target,0); //当前前缀树的值减去目标值  10-22  代表当前节点的前缀和为 -12
            map.put(count,map.getOrDefault(count,0)+1); //key就是当前前缀和  将当前前缀和的值保存
            int left=dfs(node.left,count); //遍历左边
            int right=dfs(node.right,count);//遍历右边
            map.put(count,map.get(count)-1); //子节点回溯后应该将结果减掉 避免影响右子树结果
            return result+left+right;
    }        
}

由于二叉树的递归特殊性，会先递归到最深的子树节点，然后返回上一个节点执行右递归，那么左子结点回溯后的结果肯定不能去影响右子树的节点值的计算（因为只操作一个map，而不是为每一条路径生成map），所以就需要再回溯前将当前节点的值减掉。

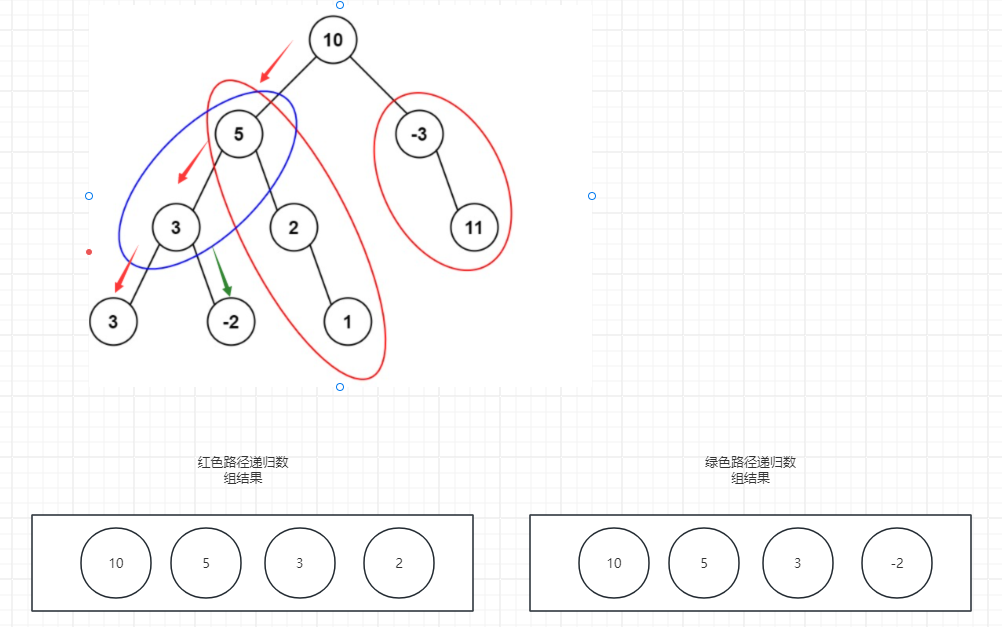
思路：

代码：

class Solution {
    public int subarraySum(int[] nums, int k) {
            HashMap<Integer,Integer> map=new HashMap<>(); //构造前缀和map  key 为前缀和
            int result=0; //结果个数
            map.put(0,1); //必须初始化 0,1
            int value=0;
            for(int i=0;i<nums.length;i++){
                value+=nums[i]; //当前前缀和的值
                result+=map.getOrDefault(value-k,0); //查看当前前缀和-k 在map中是否能找到如果有则代表是结果 取得其值 如果没有则为0
                //取值完后需要将当前前缀和put进去  key为当前前缀和  value为该前缀和的值
                map.put(value,map.getOrDefault(value,0)+1); 
            }
            return result;
    }
}