SPFA算法
概述
Dijkstra算法可以很好的解决无负权图的最短路径问题,但是如果出现了负权边,Dijkstra算法就会失效。为了更好地求解有负权边的最短路径问题,需要使用Bellman-Ford算法(简称BF算法)。但是BF算法的时间复杂度有点高,于是出现了BF算法的队列优化算法 ,也叫SPFA算法(Shortest Path Faster Algorithm)。
SPFA的称呼来自 1994年西南交通大学段凡丁的论文,其实Bellman_ford提出后不久(20世纪50年代末期)就有队列优化的版本,国际上不承认这个算法是是国内提出的。所以国际上一般称呼该算法为Bellman_ford队列优化算法(Queue improved Bellman-Ford)
在学习SPFA算法之前需要先掌握Bellman-Ford算法,参见之前的博客:https://blog.csdn.net/m0_51507437/article/details/144028315
算法思想
首先回顾一下Bellman-Ford算法。BF算法需要有n-1轮迭代(n为节点数),每轮迭代对所有边进行一次松弛操作。这里就存在一个问题,并不是所有的松弛操作都是有效的。
以第一轮为例,此时已知源点到自己距离为0(dis[1] = 0)。只有从源点出去的边的松弛操作是有效的,因为它们将这一有效信息扩散了出去,并更新了和源点相邻的点的dis数组中的信息。其他和源点不直接相邻的点对应的边的松弛操作都是无效的。
因此,我们可以从这一点入手进行优化。用邻接表存储就可以快速找到从某一点出去的所有边。找到之后就对他们进行松弛操作。接下来就是以这些新扩展出来的点为起点继续找,继续松弛。因此,队列可以很好的维护这一过程(有点类似广搜)。
SPFA算法具体步骤:
- 初始化:设置一个队列Q和一个标记数组,用于标记某个点是否在队列中。同时,初始化一个数组dis,用于存储起点到某个点的最短距离,将dis数组初始化为正无穷大。
- 入队源点:将源点加入队列,并设置其最短距离为0。
- 主循环:当队列不为空时,执行以下操作:
- 从队列中取出一个节点u。
- 遍历节点u的所有邻接节点v,如果通过节点u到节点v的路径更短(即
dis[u] + weight(u, v) < dis[v]),则更新dis[v],并检查节点v是否已经在队列中,如果不在,则将其加入队列。
- 结束条件:当队列为空时,算法结束,此时所有节点的最短路径长度都已找到。
效率分析
队列优化版Bellman_Ford的时间复杂度并不稳定,效率高低依赖于图的结构。
例如如果是一个双向图,且每一个节点和所有其他节点都相连的话,那么该算法的时间复杂度就接近于Bellman_Ford 的O(N * E),N为节点数量,E为边的数量。
在这种图中,每一个节点都会重复加入队列n - 1次,因为这种图中每个节点都有n-1条指向该节点的边,每条边指向该节点,就需要加入一次队列。
所以如果图越稠密,则SPFA的效率越接近于Bellman_Ford。反之,图越稀疏,SPFA的效率就越高。
一般来说,SPFA 的时间复杂度为O(K * N),K为不定值,因为节点需要计入几次队列取决于图的稠密度。如果图是一条线形图且单向的话,每个节点的入度为1,那么只需要加入一次队列,这样时间复杂度就是O(N)。
所以SPFA在最坏的情况下是O(N * E),但一般情况下时间复杂度为O(K * N)。
代码实现
给定一个n个点m条边的有向图,图中可能存在重边和自环,边权可能为负数。
请你求出从1号点到n号点的最短距离,如果无法从1号点走到n号点,输出impossible。
注意:图中可能存在负权回路 。
输入格式
第一行包含两个整数n,m。
接下来m行,每行包含三个整数x,y,z,表示存在一条从点x到点y的有向边,边长为z。
点的编号为1∼n。
输出格式
输出一个整数,表示从1号点到n号点的最短距离。如果不存在满足条件的路径,则输出impossible。
输入样例:
6 7
5 6 -2
1 2 1
5 3 1
2 5 2
2 4 -3
4 6 4
1 3 5
输出样例:
1
通过代码:
#include <iostream>
#include <vector>
#include <list>
#include <queue>
#include <climits>
using namespace std;
struct Edge
{
int to, w;
Edge(int y, int z) : to(y), w(z) {}
};
int main()
{
int n, m; // n个节点,m条边
cin >> n >> m;
vector<list<Edge>> graph(n + 1); // 邻接表存储图
vector<int> dis(n + 1, INT_MAX); // 目前每个点到源点的距离
vector<bool> inqueue(n + 1, false); // 标记每个点是否在队列里
dis[1] = 0; // 源点到自己为0
int x, y, z;
for (int i = 0; i < m; i++)
{
cin >> x >> y >> z;
graph[x].push_back(Edge(y, z));
}
queue<int> q;
q.push(1); // 起点入队
while (!q.empty())
{
int node = q.front();
q.pop();
inqueue[node] = false; // 出队取消标记
for (Edge edge : graph[node])
{
dis[edge.to] = min(dis[edge.to], dis[node] + edge.w); // 一次松弛操作
if (!inqueue[edge.to]) // 不在队列里的入队
{
q.push(edge.to);
inqueue[edge.to] = true;
}
}
}
if (dis[n] == INT_MAX)
cout << "impossible" << endl;
else
cout << dis[n] << endl;
return 0;
}
判断负权回路
首先回顾一下负权回路:图中带环且环中所有边的权重和为负。如下图所示。
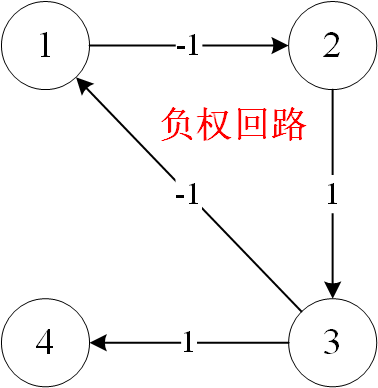
在极端情况下,即:所有节点都与其他节点相连,每个节点的入度为n-1(n为节点数量),所以每个节点最多加入n-1次队列。那么如果节点加入队列的次数超过了 n-1次 ,该图就一定有负权回路。
所以用一个数组记录每个节点加入队列的次数,并在循环里判断是否超过n-1次即可。
实现代码如下:
#include <iostream>
#include <vector>
#include <list>
#include <queue>
#include <climits>
using namespace std;
struct Edge
{
int to, w;
Edge(int y, int z) : to(y), w(z) {}
};
int main()
{
int n, m; // n个节点,m条边
cin >> n >> m;
vector<list<Edge>> graph(n + 1); // 邻接表存储图
vector<int> dis(n + 1, INT_MAX); // 目前每个点到源点的距离
vector<bool> inqueue(n + 1, false); // 标记每个点是否在队列里
vector<int> count(n + 1, 0); // 记录每个节点入队几次
dis[1] = 0; // 源点到自己为0
int x, y, z;
for (int i = 0; i < m; i++)
{
cin >> x >> y >> z;
graph[x].push_back(Edge(y, z));
}
queue<int> q;
q.push(1); // 起点入队
bool flag = false; // 标记是否存在负权回路
while (!q.empty())
{
int node = q.front();
q.pop();
inqueue[node] = false; // 出队取消标记
for (Edge edge : graph[node])
{
dis[edge.to] = min(dis[edge.to], dis[node] + edge.w); // 一次松弛操作
if (!inqueue[edge.to]) // 不在队列里的入队
{
q.push(edge.to);
inqueue[edge.to] = true;
count[edge.to]++;
if (count[edge.to] > n - 1) // 如果加入队列次数超过n-1次,就说明该图存在负权回路
{
flag = true;
while (!q.empty())
q.pop();
break;
}
}
}
}
if (flag)
cout << "circle" << endl;
else if (dis[n] == INT_MAX)
cout << "unconnected" << endl;
else
cout << dis[n] << endl;
return 0;
}
