机器学习算法基础知识1：决策树

一、本文内容与前置知识点

1. 本文内容

介绍决策树是什么，使用场景有哪些

2. 前置知识点

1. 概率论基本知识：信息熵增益

二、场景描述

• 鸢尾花的类别存在Setosa，Versicolour，Virginica三种，我们希望制作一个模型，对鸢尾花进行分类。
• 我们会提供一些我们已经采集的样本，并且手动提取了每朵花的部分特征，数据集一共包括150个样本，每个样本包括花萼长度，花萼宽度，花瓣长度，花瓣宽度特征，以及对应鸢尾花类别的标签第5列为鸢尾花的类别（包括Setosa，Versicolour，Virginica三类）。

三、决策树的训练

我们把150个样本，取出120个作为训练集，来进行决策树的训练，目的希望决策树这个分类器有如下效果：
（1）对于训练集的样本能有比较好的分类效果
（2）对于测试集的样本能有比较好的分类效果

1. 决策树训练方式

（1）分类原则-Gini

每一层会选取一个特征进行分类，以二分类为主，分类原则遵循贪心算法，希望尽可能的把样本区分开。
使用了基尼系数作为样本分类效果的评估指标：
$$Gini=1-\sum _{i=1}^n{p}_i^2$$
可以看到样本分布越均匀，基尼系数越大，我们希望完成分类，也就是让基尼系数尽可能小，样本完全由同一类别构成的时候，基尼系数为0。

（2）分类原则-entropy

信息熵，同样的，样本的分布越均匀熵越大。
$$Entropy=-\sum _{i=0}^n{p}_i{\log }_2(p_i)$$

（3）加权系数-样本量

直观的考虑以下场景，三个类别个数分别为9，4，2，记为(9,4,2)：
下一级分类有两种方案：
方案A：[(1,0,0),(8,4,2)]
方案B：[(8,0,0),(1,4,2)]
两种方案信息熵或基尼系数的加和相同，但是显然B尽可能多的把第一类分出去了，直观会认为更好。
从上述可以看出，分出的堆的大小同样应该被考虑进去进行loss的计算。

所以实际的loss会被记录为(二分类为例)：
$$loss=mGin{i}_m+nGin{i}_n$$
m和n分别是所分出两堆的大小，用该等式计算信息量显然方案B会更小，方案B更合适。

（3）程序是如何实现的

程序枚举每个特征和阈值，在每层的数据中找出信息量最小的分类方式进行分类，逐层以这种贪心的方式进行分类
我们只要当好调包侠就行，不需要反复造轮子。

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn import tree
import matplotlib.pyplot as plt

# 加载数据集
iris = load_iris()
X, y = iris.data, iris.target

# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 构建决策树分类器
clf = DecisionTreeClassifier(criterion='entropy', max_depth=3, random_state=42)
clf.fit(X_train, y_train)
print(iris.feature_names)
print(iris.target_names)
# 可视化决策树
plt.figure(figsize=(12, 8))
tree.plot_tree(clf, feature_names=iris.feature_names, class_names=iris.target_names, filled=True)
plt.show()

# 测试准确率
accuracy = clf.score(X_test, y_test)
print("测试集准确率:", accuracy)

2. 决策树构建结果

（1）决策树常用作分类器，通过逐级进行条件判断的方式，将样本进行逐级分类，如下图：
（2）这个决策树通过逐级二分类的方式，将鸢尾花按照不同的特征进行分类。
（3）每个子节点得出最终分类结果，这个决策树是三层的，对于整个鸢尾花的分类结果上看，120个样本大部分都得到了很好的分类。但是有一个白色的子节点，仍然含有4朵花是vriginica，被识别成了versicolor。

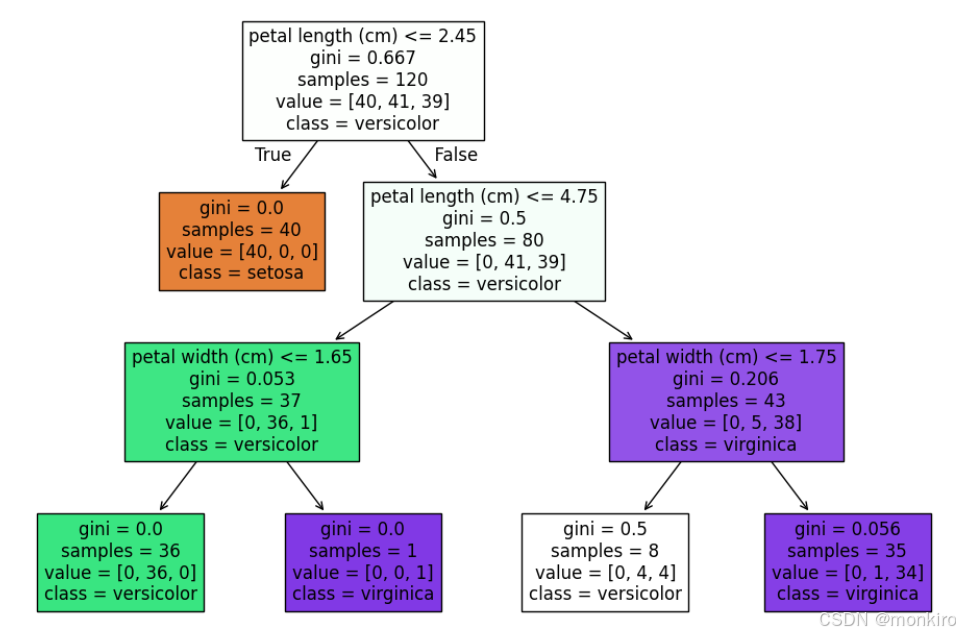
方框中每一行分别是

1. 分类条件
2. 基尼系数（表征样本的无序程度，假设样本全都是同一种，则基尼系数=0）
3. 样本数
4. 第四行是当前节点在分类中的归属类别。

三、测试集验证

把测试集放进去进行训练得到结果，验证决策树的训练效果

accuracy = clf.score(X_test, y_test)
print("测试集准确率:", accuracy)

四、其他知识

1. 这里只介绍了决策树用于分类的做法，事实上还可以用于回归。
2. 这里只介绍了Gini和信息熵增益的训练方式，事实上还有别的。
3. 树的构建最大层数是需要合理考虑的，过浅分不出来，过深会由于一些极端点导致过拟合，设置合理的层数，允许一些训练集的点分类错误，都是常见的策略。
4. 决策树本质上是不断的在线性空间进行线性分割，这一点有一点像SVM？
5. 合理的树的深度会使用交叉验证的方式来进行估算

五、参考文献

五分钟机器学习：决策树