程序猿成长之路之密码学篇-AES算法介绍
DES算法介绍总算告一段落了,DES由于它的密钥每组只有64位,安全性能堪忧,为此阿美丽卡(美国)相继推出了3DES、AES等对称加密算法。3DES为此不在赘述,有兴趣的小伙伴可以网上找找“攻略”。接下来介绍一下AES加解密算法。
如果有小伙伴对DES不熟的,我放上之前的DES介绍文章:
https://blog.csdn.net/qq_31236027/article/details/128209185
什么是AES算法,AES算法与DES算法的异同点有哪些?
AES是阿美丽卡(美国)推出的高级加密算法,于2001年11月26日发布。该算法牛逼的地方在于它的密钥不长但暴力破解难度指数级增长。它的密钥虽说不长,但相较于拉跨的DES算法而言还是扩充了不少位。密钥的长度分为多个版本:128位、192位和256位。但是明文始终按照128位运算,并且加密的轮数会随着密钥长度的变化而变化,如下图所示:
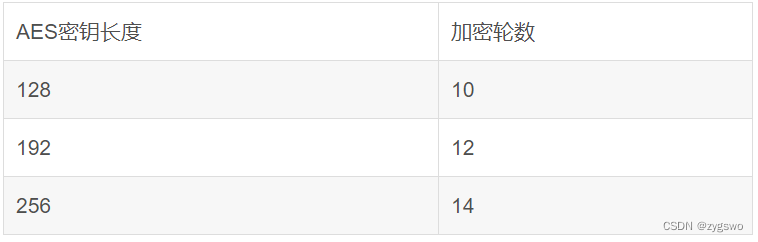
接下去讲讲AES和DES算法的异同点:
AES与DES区别:
- 看过我之前介绍DES文章的小伙伴应该知道,DES是要将明文二进制流分成左半部分和右半部分,之后再通过置换、f函数运算、位异或等操作完成加密,解密亦是如此。而AES则不是如此,它是通过对整个明文进行整体处理生成密文,此外采用的运算主要为字节代换、行移位、列混合等效率可能会更高。
- AES密钥至少为128位,而DES为64位,AES比DES更好的可以应对暴力破解。AES加密轮数为16轮,而AES密钥加密轮数最大为14轮,提升了加解密效率。
AES与DES的相同点:
- 都是对称加密算法,这点毫无疑问。
- AES与DES都使用到了S盒,并且S盒的设计直接决定了算法的好坏。
- AES与DES都是用到了循环移位,并且遵循了香农的扩散和混淆原则,
AES算法整体的流程概述(详解见后续文章)
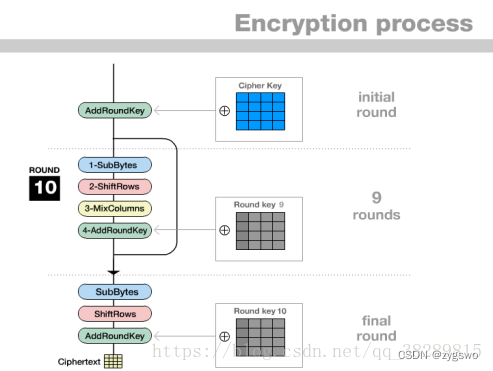
明文的加密
- 字节代替
- 行移位
- 列混合
- 轮密钥加
简单解释一下上面的图:
首先在初始加密轮进行一次轮密钥加,初始明文矩阵行数为4,因为为128位分组加密,每列32位,密钥矩阵行数也为4,与初始明文矩阵进行一次异或运算。之后进行s盒的字节代替,增加扩散,s盒设计的好坏直接决定算法优劣,之后就是行移位和列混合,再次进行轮密钥加,重复该过程直至第九轮,最后一轮只进行字节代替、行移位和轮密钥加。得到最终的矩阵密文结果。
密钥的扩展
详见 https://blog.csdn.net/qq_40739219/article/details/120860258
AES算法有关的数学基础知识
群、环、域
参考自https://blog.csdn.net/weixin_44584702/article/details/122709135
群与交换群
群G,是定义了一个二元运算【可以任意】的集合,记为{G,·}【注意:以下二元运算都记作这个标记】,G中每一个序偶(a,b)通过运算生成G中的元素(a,b),如果有a·b = b·a则称之为交换群。
性质如下:
封闭性:如果a和b都属于G,则a·b也属于G,如3,4属于某一群,那么3和4经过某一二元运算后的结果也得属于这个群
结合律:对于G中任意元素a、b、c,都有a·(b·c)=(a·b)·c成立单位元:G中存在一个元素e,对于G中任意元素a,都有a·e=e·a=a成立。
逆元:对于G中任意元素a,G中都存在一个元素a‘,使得下式成立a·a’=a’·a=e(单位元,加法为0,乘法为1)。
环与整环
环R,记为{R,+,x},是一个有两个二元运算的集合,具有以下性质和定律
R关于加法是一个交换群;因此R满足从上述交换群的所有原则。
乘法的封闭性:如果a和b都属于R,则a*b也属于R。
乘法的结合律:对于R中任意元素a、b、c,有 a(bc)=(ab)c成立。
分配律:对于R中的任意元素a、b、c,下面两个式子总成立 a (b+c) = ab + ac; (a+b) c = ac + bc
如果还满足以下条件,则称之为整环:
乘法交换律:对于R中任意元素a、b,有ab=ba成立。
乘法单位元:在R中存在元素1,使得对于R中的任意元素a,有a1=1a=a成立。
无零因子:如果有R中元素a、b,且ab=0,则必有a=0或b=0。‘
域与伽罗瓦域
域F,记为{F,+,x},是有两个二元运算的集合,并且前提是一个整环,满足对于F中的任意元素a(除0以外),F中都存在一个逆元a’,使得a*a’ = e(单位元)
在抽象代数中,域是一种可进行加、减、乘和除运算的代数结构。域的概念是数域以及四则运算的推广。包含有限个元素的域被称为有限域。 有限域中元素的个数称为有限域的阶。尽管存在有无限个元素的无限域,但只有有限域在密码编码学中得到了广泛的应用。每个有限域的阶必为素数的幂,即有限域的阶可表示为pⁿ(p是素数、n是正整数),该有限域通常称为伽罗瓦域(Galois Fields),记为GF(pⁿ)。当n=1时,存在有限域GF(p),也称为素数域。【来自百度百科】

是不是看的有点晕了?哈哈,现在我来解释一下:
群,可以理解为最基本的单位,它只能容纳一个二元运算,然后呢群里的元素都可以进行这种二元运算成为另一个群内的元素比如,{Z, +}这个就是一个群,但是是一个无限群,因为里面是由所有整数组成的。那么我们有3属于这个群,4也属于这个群,3+4也属于这个群, 并且这个群也属于交换群(因为3+4=4+3)。
那么,什么是环?
举个例子,{Z,+,*}就是一个环,在加法层面上{Z,+}属于交换群,因为加法层面上有逆元和单位元,如2的加法逆元为-2,加法单位元为0。并且满足封闭性和结合律原则。但在乘法上不满足交换群,因为2的逆元为1/2,不在群{Z,*}里。见上图的最上方的那个流程。
什么是整环?
简单讲,如果一个群既关于加法是交换群,关于乘法无乘法逆元,那么可以称为整环。如图中间的那个流程。
什么是域?
域可以理解为包含乘法逆元的整环。具有以上所有特征和原则。
什么是伽罗瓦域?
- 它是一个有限域
- 它的阶(其中元素的个数)必为素数的幂。为什么呢?我们知道有限域是基于素数域扩展而来的,例如4 = 2+2,6=23,。也就是它的基域为Zp(p为素数),那么基于域的概念,它满足(Zp, +,),因此我们可以认为它的阶为p^n. 当n=1时,该域就为素数域。素数域的阶等于它本身。
为何AES加解密需要用到伽罗瓦域?
- 域内数字有限好处理
- 阶为素数
- 有加法、乘法逆元(可以求逆)
最后提一句,加解密一般使用素数域GF§ 或者扩展域GF(2^m), 为什么用扩展域?大家可以想一想,我之后再做补充。
——————————————————————未完待续——————————————————————
