相同的树及延伸题型（C语言详解版）

从LeetCode 100和101看二叉树的比较与对称性判断

今天要讲的是leetcode100.相同的树，并且本文章还会讲到延伸题型leetcode101.对称二叉树。本文章编写用的是C语言，大家主要是学习思路，学习过后可以自己点击链接测试，并且做一些对应的生题，现在就让我们开始吧！

一、题目简介

LeetCode 100：相同的树

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：

输入：p = [1,2,1], q = [1,1,2]
输出：false

提示：

• 两棵树上的节点数目都在范围 [0, 100] 内
• -104 <= Node.val <= 104

LeetCode 101:   对称二叉树

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

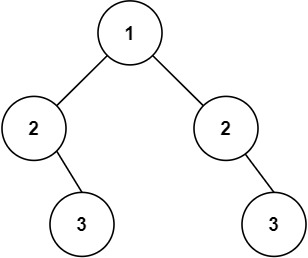
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

• 树中节点数目在范围 [1, 1000] 内
• -100 <= Node.val <= 100

进阶：你可以运用递归和迭代两种方法解决这个问题吗？

二、思路详解

题目一：LeetCode 100（相同的树）

1. 问题分析

这道题里有一个小坑，如果我们单纯只通过遍历来比对是否相等的话，是无法保证二叉树的结构相同的，仅仅只能保证该颗二叉树所包含的节点数值是一致的，但是我们将一颗树分为多个部分来比对就会方便很多，将两棵树对应的左子树与左子树比对，右子树和右子树比对。

2. 解题思路

我们可以使用递归的方法来解决这个问题。递归的基本思路如下：

• 如果两个节点都为空，返回 true。

• 如果一个节点为空而另一个不为空，返回 false。

• 如果两个节点的值不同，返回 false。

• 递归地比较左子树和右子树。

3. C语言实现

#include <stdbool.h>

// 定义二叉树节点结构
typedef struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
} TreeNode;

// 递归函数，比较两个节点
bool isSameTree(TreeNode* p, TreeNode* q) {
    // 如果两个节点都为空，返回true
    if (p == NULL && q == NULL) {
        return true;
    }
    // 如果一个为空，另一个不为空，返回false
    if (p == NULL || q == NULL) {
        return false;
    }
    // 如果两个节点的值不同，返回false
    if (p->val != q->val) {
        return false;
    }
    // 递归比较左子树和右子树
    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

题目二：LeetCode 101（对称二叉树）

1. 问题分析

这道题与上一道题（LeetCode 100：相同的树）是很相似，但有两个关键的不同点：

1. 参数不同：这道题只传入一个根节点，即只有一棵树。

2. 判断条件不同：这道题要求判断的是对称二叉树，即镜像相同。具体来说，左子树的左节点应该与右子树的右节点相同，左子树的右节点应该与右子树的左节点相同。

2. 解题思路

为了解决上述两个不同点，我们可以通过构造一个新的函数来实现将一棵树“一分为二”，再对两侧的左右子树进行比较。递归的基本思路如下：

1. 递归终止条件：

   • 如果两个节点都为空，返回 true，表示这部分是镜像对称的。

   • 如果一个节点为空而另一个不为空，返回 false，表示这部分不对称。

2. 递归逻辑：

   • 如果两个节点的值相同，继续递归比较左子树的左节点与右子树的右节点，以及左子树的右节点与右子树的左节点。

   • 如果两个节点的值不同，直接返回 false。

3. C语言实现

#include <stdbool.h>

// 定义二叉树节点结构
typedef struct TreeNode {
    int val;                     // 节点的值
    struct TreeNode *left;       // 指向左子节点的指针
    struct TreeNode *right;      // 指向右子节点的指针
} TreeNode;

// 辅助函数：检查两个节点是否镜像对称
bool check(struct TreeNode* p, struct TreeNode* q) {
    // 如果两个节点都为空，说明这部分是镜像对称的
    if (p == NULL && q == NULL) {
        return true;
    }
    // 如果一个为空，另一个不为空，说明这部分不对称
    if (p == NULL || q == NULL) {
        return false;
    }
    // 如果两个节点的值相同，继续递归检查子节点
    if (p->val == q->val) {
        // 递归检查左子树的左节点与右子树的右节点
        // 以及左子树的右节点与右子树的左节点
        return check(p->left, q->right) && check(p->right, q->left);
    }
    // 如果两个节点的值不同，直接返回false
    return false;
}

// 主函数：判断整棵树是否对称
bool isSymmetric(struct TreeNode* root) {
    // 从根节点开始，调用辅助函数检查整棵树是否对称
    return check(root, root);
}

#include <stdbool.h>

// 定义二叉树节点结构
typedef struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
} TreeNode;

// 使用迭代方法（层次遍历）判断二叉树是否对称
bool isSymmetric(struct TreeNode* root) {
    // 如果根节点为空，直接返回 true（空树是对称的）
    if (root == NULL) return true;

    // 使用数组模拟队列
    struct TreeNode* queue[1000];
    // head 和 tail 分别指向队列的头部和尾部
    int head = 0, tail = 0;

    // 将根节点的左右子树加入队列
    queue[tail++] = root->left;
    queue[tail++] = root->right;

    // 循环结束条件：队列为空（head == tail）
    while (head != tail) {
        // 从队列中取出两个节点进行比较
        struct TreeNode* leftNode = queue[head++];
        struct TreeNode* rightNode = queue[head++];

        // 如果一个节点为空而另一个不为空，说明不对称，返回 false
        if (leftNode == NULL && rightNode != NULL) return false;
        if (leftNode != NULL && rightNode == NULL) return false;

        // 如果两个节点都为空，跳过本轮循环，继续下一对节点的比较
        if (leftNode == NULL && rightNode == NULL) continue;

        // 如果两个节点的值不相等，说明不对称，返回 false
        if (leftNode->val != rightNode->val) return false;

        // 将左节点的左子节点和右节点的右子节点加入队列
        queue[tail++] = leftNode->left;
        queue[tail++] = rightNode->right;

        // 将左节点的右子节点和右节点的左子节点加入队列
        queue[tail++] = leftNode->right;
        queue[tail++] = rightNode->left;
    }

    // 如果队列为空且没有发现不对称的情况，返回 true
    return true;
}