对机载预警雷达STAP的慢时调频干扰matlab
对机载预警雷达STAP的慢时调频干扰matlab
- STAP基本原理流程
- 慢时调频干扰模型
- 慢时调频干扰STAP仿真matlab
STAP基本原理流程
假设天线阵有N个阵元,一个CPI包含M个脉冲,STAP的具体计算流程如下。
(1) 确定待检测单元,明确该CUT的距离、方位。
(2) 选取一个多普勒频率
f
d
f_d
fd,并结合(1)得到对应的空时导向矢量:
s
(
θ
,
f
d
)
=
b
(
f
d
)
⊗
a
(
θ
)
s(\theta,f_d)=b(f_d) \otimes a(\theta)
s(θ,fd)=b(fd)⊗a(θ)
式中,
⊗
\otimes
⊗是Kronecker运算符;
b
(
f
d
)
b(f_d)
b(fd)和
a
(
θ
)
a(\theta)
a(θ)分别是时间、空间导向矢量,即
a
(
θ
)
=
[
1
,
e
j
2
π
f
s
p
∗
1
,
.
.
.
,
e
j
2
π
f
s
p
∗
(
N
−
1
)
]
T
b
(
f
d
)
=
[
1
,
e
j
2
π
f
d
∗
1
,
.
.
.
,
e
j
2
π
f
d
∗
(
M
−
1
)
]
T
f
s
p
=
d
c
o
s
(
θ
)
λ
f
d
=
f
d
T
a(\theta)=[1,e^{j2\pi f_{sp}*1},...,e^{j2\pi f_{sp}*(N-1)}]^T\\b(f_d)=[1,e^{j2\pi f_{d}*1},...,e^{j2\pi f_{d}*(M-1)}]^T\\f_{sp}=\frac{dcos(\theta)}{\lambda}\\\ f_d=\frac{f_d}{T}
a(θ)=[1,ej2πfsp∗1,...,ej2πfsp∗(N−1)]Tb(fd)=[1,ej2πfd∗1,...,ej2πfd∗(M−1)]Tfsp=λdcos(θ) fd=Tfd
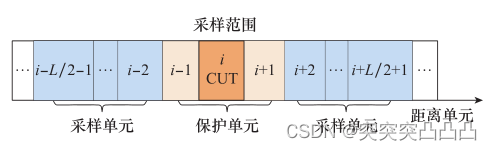
(3)确定取样范围。将CUT及前后若干个单位作为待保护单元,在待保护单元以外的距离单元进行背景取样。
(4)估计协方差矩阵。根据已采集的背景样本估计杂波协方差矩阵:
R
=
1
L
∑
x
l
x
l
H
R=\frac{1}{L}\sum x_l x_l^{H}
R=L1∑xlxlH
(5)计算权值。权重计算式为
w
=
μ
R
−
1
s
(
θ
,
f
d
)
w=\mu R^{-1}s(\theta,f_d)
w=μR−1s(θ,fd)
(6)选取下一个多普勒频率,重新执行(2)~(5)
(7)对同一个CUT所有多普勒频率输出进行比较,输出值超过检测门限的认为有回波目标输出。
(8)选取下一个距离,重新(1)~(7),直到所有的距离单元都计算完毕,
(9)选取下一个方位,重新(1)~(8)。
慢时调频干扰模型
假设干扰机收到的信号为
E
(
t
)
E(t)
E(t),那么发射的干扰脉冲可表示为每个周期干扰脉冲的叠加,即
J
(
t
)
=
∑
m
=
1
M
J
m
(
t
−
m
T
)
J(t)=\sum^M_{m=1} J_m(t-mT)
J(t)=m=1∑MJm(t−mT)
式中,
J
m
(
t
)
J_m(t)
Jm(t)是第m个PRI中发射的干扰信号,可表示为
J
m
(
t
)
=
∑
q
=
1
Q
A
q
E
(
t
−
τ
q
)
e
j
2
π
f
q
∗
m
J_m(t)=\sum^{Q}_{q=1}A_qE(t-\tau_q) e^{j2\pi f_q*m}
Jm(t)=q=1∑QAqE(t−τq)ej2πfq∗m
式中,
f
q
f_q
fq是第q个干扰脉冲的多普勒频率
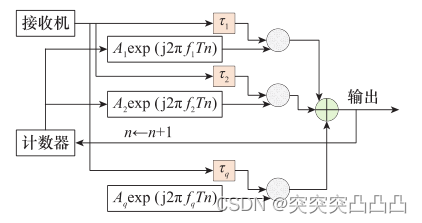
慢时调频的原理图如图。先将计数器初始化,产生一系列复数移频因子,再将接收到的目标信号按预设值进行时延后,与移频因子相乘,最后将各干扰脉冲相加输出,并将计数器加1,开始下一个PRI的干扰脉冲输出。
慢时调频干扰STAP仿真matlab
仿真参数:
采样率4MHz,载频8GHz,脉宽1us,带宽2MHz,脉冲重复频率5kHz,周期数20,阵元个数6;
干扰假目标个数30,慢时调频干扰范围100-200Hz
(1)未经过慢时调频干扰的STAP处理干扰效果

(2)经过慢时调频干扰后的STAP处理干扰效果

可以看出,未经过慢时调频干扰时,STAP处理会对密集假目标干扰产生对消效果,导致干扰效果不佳;而经过慢时调频干扰后,STAP处理无法有效的抑制干扰,干扰具有一定的效果。
