Leetcode.764 最大加号标志
题目链接
Leetcode.764 最大加号标志 Rating : 1753
题目描述
在一个 n x n的矩阵 grid中,除了在数组 mines中给出的元素为 0,其他每个元素都为 1。mines[i] = [xi, yi]表示 grid[xi][yi] == 0
返回 grid中包含 1 的最大的 轴对齐 加号标志的阶数 。如果未找到加号标志,则返回 0 。
一个 k阶由 1 组成的 “轴对称”加号标志 具有中心网格 grid[r][c] == 1,以及4个从中心向上、向下、向左、向右延伸,长度为 k-1,由 1 组成的臂。注意,只有加号标志的所有网格要求为 1 ,别的网格可能为 0 也可能为 1 。
示例 1:
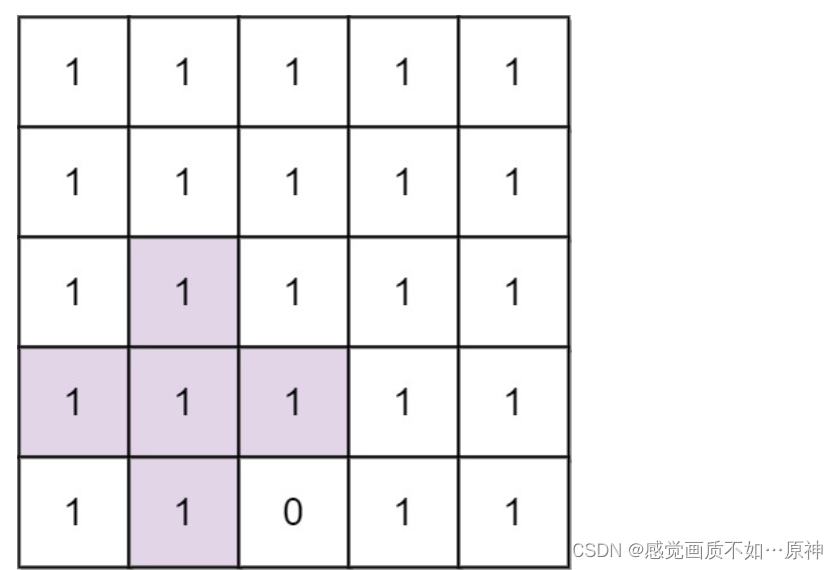
输入: n = 5, mines = [[4, 2]]
输出: 2
解释: 在上面的网格中,最大加号标志的阶只能是2。一个标志已在图中标出。
示例 2:

输入: n = 1, mines = [[0, 0]]
输出: 0
解释: 没有加号标志,返回 0 。
提示:
- 1 < = n < = 500 1 <= n <= 500 1<=n<=500
- 1 < = m i n e s . l e n g t h < = 5000 1 <= mines.length <= 5000 1<=mines.length<=5000
- 0 < = x i , y i < n 0 <= xi, yi < n 0<=xi,yi<n
- 每一对 (
xi, yi) 都 不重复
解法:动态规划
定义 f ( i , j ) f(i,j) f(i,j) 为能形成 “加号” 的最大阶数。则最终的答案为, m a x ( f ( i , j ) ) max(f(i,j)) max(f(i,j))。
时间复杂度: O ( n 2 ) O(n^2) O(n2)
C++代码:
class Solution {
public:
int orderOfLargestPlusSign(int n, vector<vector<int>>& mines) {
vector<vector<int>> g(n,vector<int>(n,1));
for(auto &e:mines){
int x = e[0] , y = e[1];
g[x][y] = 0;
}
vector<vector<int>> f(n,vector<int>(n,n));
for(int i = 0;i < n;i++){
int up = 0,down = 0,left = 0,right = 0;
for(int j = 0,k = n - 1;j < n;j++,k--){
left = g[i][j] ? left + 1 : 0;
right = g[i][k] ? right + 1 : 0;
up = g[j][i] ? up + 1 : 0;
down = g[k][i] ? down + 1 : 0;
f[i][j] = min(f[i][j],left);
f[i][k] = min(f[i][k],right);
f[j][i] = min(f[j][i],up);
f[k][i] = min(f[k][i],down);
}
}
int ans = 0;
for(int i = 0;i < n;i++){
for(int j = 0;j < n;j++) ans = max(ans,f[i][j]);
}
return ans;
}
};
