【C++笔试强训】第五天
选择题

解析:本题考查
do while循环及后置++。刚开始x = 1,先进入循环中,后置++是先使用再++,所以printf输出结果为 1。++后x的值变为2,经while(x–)后又变为1,再次进入循环…… 所以该程序将会陷入死循环。

解析:
sizeof是一个操作符,用于计算变量或类型的大小,一般单位为字节,通常用于计算内存大小。strlen是函数,用于计算字符串的长度,只统计字符串中字符的数量,不包括结尾的空字符。sizeof是用于计算内存占用,strlen主要是用于计算字符串的长度。sizeof(dog)计算的是整个字符数组所占内存大小,字符串中的’\0’算是一个字符,计算字符串大小的时候也要加上末尾的结束字符’\0’;strlen遇见’\0’就停止。所以选A。

解析:strcpy ( char * destination, const char * source )函数是覆盖拷贝,将source全覆盖拷贝到destination,会把’\0’也拷过去,且必须考虑destination的空间够不够(destination的空间必须>=source的空间)。
strcat( char * destination, const char * source ) 为追加拷贝函数,将source追加到目标空间后面,目标空间必须足够大,能容纳下源字符串的内容。
strcat是字符串追加的库函数,第一个参数为被追加字符的首地址,从首地址开始字符串的结尾,第二个参数是追加字符的首地址,从此位置向被追加的位置开始进行追加。成功就返回被追加字符的首地址。题目strcat(p1+2,p2+1)中,p2+1表示指向字符串"ABCD"中B的地址,p1+2表示指向"abcd"中c的地址即被追加字符首地址,所以这句代码的意思就是将"BCD"追加到"cd"的后面,然后返回被追加字符的首地址,追加后的结果为:cdBCD,返回的是c的地址。然后进行拷贝,从str+2的位置进行拷贝。最后选D。

解析:
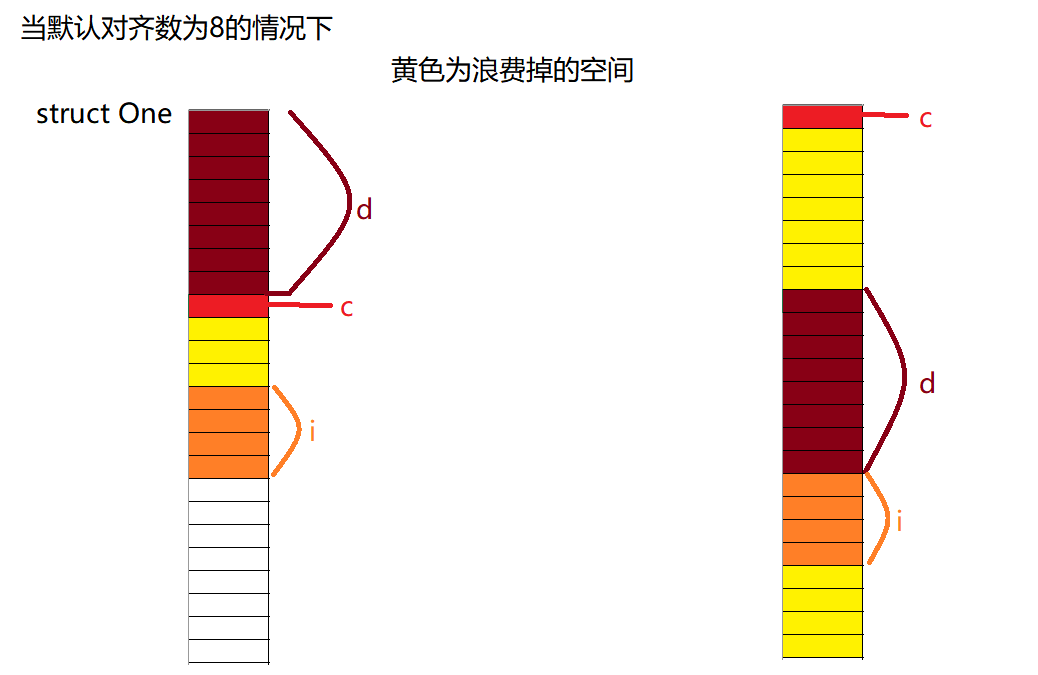
n数组可表示为上图所示,int (*p)[3]表示这是一个数组指针,存放的是数组的地址。p指向数组的第0行,
p[0][0]等价于n[0][0],即是第1行第1个元素,即10;*(p[0]+1)也可以用p[0][1]或*(*(p+0)+1)表示,就是第1行第2个元素,即20;(*p)[2]可以表示为*(p+0)[2],即第1行第3个元素30,所以答案选B。

解析:C/C++程序的入口函数是main函数;main函数可以放在程序的任意位置;要调用的函数可以不在main函数中,也可以在别的函数中调用。

解析:在定义的时候,由于a是int类型,字符’1’会发生隐式类型转换,转换成整形,b、c也同样会发生类型抓换;传参的时候也会发生隐式类型转换,转化成对应的字符。fun(a,b)返回的是’1’,fun(b,c)返回的是’1’,最后就是fun(‘1’,‘1’),所以最后输出的就是字符’1’。

解析:
int* pa[5]是一个指针数组,具有5个元素,每个元素都是int类型的指针。

解析:
pragma pack()设置默认对齐数。结构体的内存对齐规则:
(1)结构体的第一个成员直接对齐到相对于结构体变量起始位置为0的偏移处。
(2)从第二个成员开始,要对齐到某个对齐数的整数倍的偏移处。(对齐数:结构体成员自身大小和默认对齐数中的较小值,VS下默认对齐数是8个字节;Linux环境下默认不设对齐数,对齐数是结构体成员的自身大小)
(3)结构体的总大小必须是最大对齐数的整数倍。
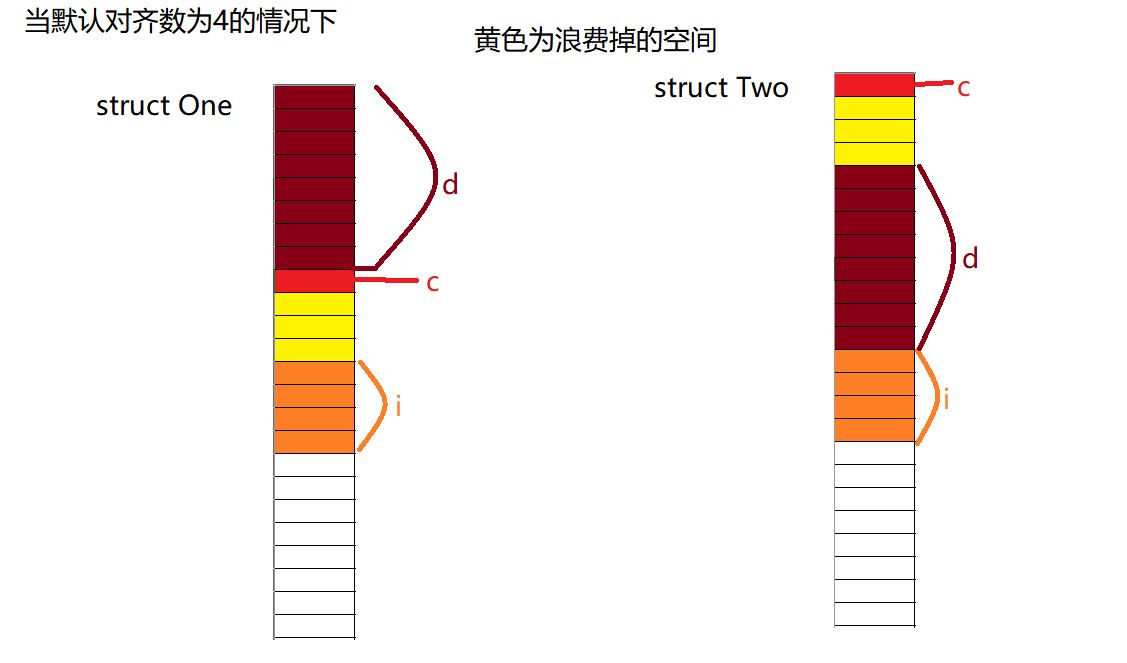
(4)如果嵌套了结构体的情况,嵌套的结构体对齐到最大对齐数的整数倍处,结构体的整体大小就是所有对齐数(含嵌套结构体的对齐数)中最大对齐数的整数倍。(1)对齐数为4的情况下:
struct One中成员变量d的类型为double,占8个字节;char类型成员变量c占1个字节;int类型成员变量i占4个字节,但是必须从对齐数的整数倍开始,所以从12开始向后偏移4个字节,所以总共占了16个字节;
struct Two中char类型成员变量c占1个字节;成员变量d的类型为double,占8个字节,但是由结构体内存对齐规则的(2)可知,从第二个成员变量开始,要对齐到某个对齐数的整数倍的偏移处,对齐数为成员变量自身大小(8)和默认对齐数(4)中的较小值,即4。所以从4开始向后偏移8个字节;int类型成员变量i占4个字节,也要从对齐数的整数倍开始,所以从12开始向后偏移4个字节,所以总共占了16个字节。
(2)对齐数为8的情况下:
struct One中成员变量d的类型为double,占8个字节;char类型成员变量c占1个字节;int类型成员变量i占4个字节,但是必须从4的整数倍开始,所以从12开始向后偏移4个字节,所以总共占了16个字节;
struct Two中char类型成员变量c占1个字节;成员变量d的类型为double,占8个字节,但是由结构体内存对齐规则的(2)可知,从第二个成员变量开始,要对齐到某个对齐数的整数倍的偏移处,对齐数为成员变量自身大小(8)和默认对齐数(8)中的较小值,即8。所以从8开始向后偏移8个字节;int类型成员变量i占4个字节,也要从对齐数的整数倍开始,即从4的整数倍开始,所以从16开始向后偏移4个字节,所以总共占了24个字节。

解析:
a[i]可以表示为*(a + i),a[i][j]可以表示为*(*(a + i) + j)以此类推……,需要一层一层的解引用。

解析:
预处理是将宏定义展开,将被包含的文件插入到该编译指令的位置等;
编译就是把预处理完的文件,进行语法分析、词法分析、语义分析及优化后生成相应的汇编代码文件,这个过程是整个程序构建的核心过程,也是最复杂的部分;
汇编是将汇编代码文件转变成机器可以执行的指令文件,即目标文件;
链接:将这些模块组装起来的过程就是链接,链接的时候去找对应函数,未定义的函数就会报错——该函数没有定义。
编程题
1.统计回文

解析:保存刚开始的s1,从头到尾将s2插入到s1中,然后翻转比较。
#include <iostream>
#include <algorithm>
#include <string>
using namespace std;
int main() {
string s1;
string s2;
getline(cin, s1);
getline(cin, s2);
string s3;
string s4;
s3 = s1;//刚开始保存s1,防止后续s1插入之后被改变
int count = 0;//用来记录相同次数
int i = 0;
while (i < s1.size()+1) { //i的值要比size大1,因为在字符串的最后也要插入一次
//s1 = s3;//不能在这里写
s1.insert(i, s2); //插入
s4 = s1;//插入之后赋值给s4,方便后续翻转
//翻转比较是否相同
reverse(s1.begin(), s1.end());
if (s1 == s4)
count++;
s1 = s3;
i++;
}
cout << count;
}
答案解析:什么是回文字符串,题目里面说就是一个正读和反读都一样的字符串 ,回文串也就是前后对称的字符串。本
题是判断是否是回文串的变形题。字符串本身不一定是回文,把第二个字符串插入进去看是否是回文。本题使用暴力求解方式计算即可,遍历str1,将str2 insert进入str1的每个位置,判断是否是回文,是就
++count;需要注意的是这里不能 str1.insert(i, str2),这样的话str1改变了,判断下一个位置就不对了。所
以每次使用str1拷贝构造一个str,然后str.insert(i, str2),再判断。
#include<iostream>
#include<string>
using namespace std;
// 判断是否是回文
bool IsCircleText(const string& s)
{
size_t begin = 0;
size_t end = s.size()-1;
while(begin < end)
{
if(s[begin] != s[end])
return false;
++begin;
--end;
}
return true;
}
int main()
{
std::string str1, str2;
getline(cin, str1);
getline(cin, str2);
size_t count = 0;
for(size_t i = 0; i <= str1.size(); ++i)
{
// 将字符串2插入到字符串1的每个位置,再判断是否是回文
string str = str1;
str.insert(i, str2);
if(IsCircleText(str))
}
cout<<count<<endl;
return 0;
}
2.连续最大和
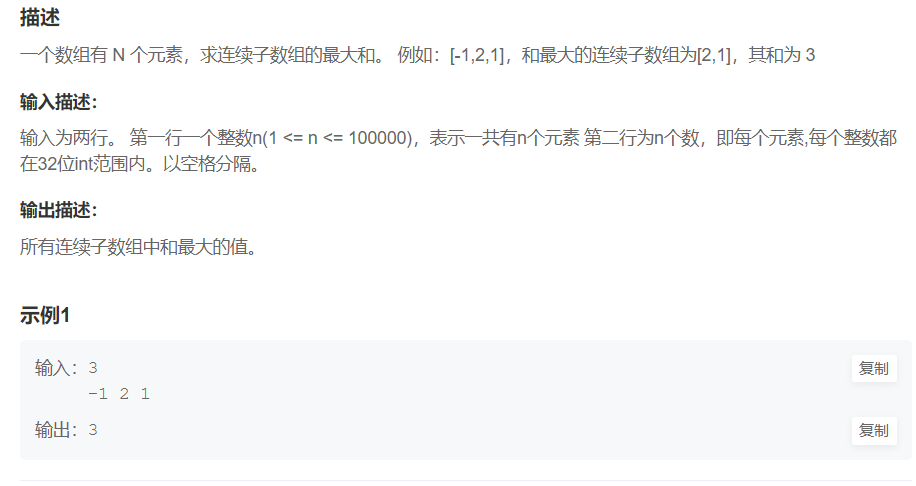
答案解析:本题是一个经典的动规问题,简称dp问题,但是不要害怕,这个问题是非常简单的dp问题,而且经常会考察,所以大家一定要把这个题做会。本题题意很简单,就是求哪一段的子数组的和最大。
【解题思路】:状态方程式: max( dp[ i ] ) = getMax( max( dp[ i -1 ] ) + arr[ i ] ,arr[ i ] )
dp[i] 就是以数组下标为 i 的数做为结尾的最大子序列和,注意是以 i 为结尾,比如说现在有一个数组{6,-3,-2,7,-15,1,2,2},dp[2]就是以-2为结尾的,那么显然dp[2]的最大值就是1(6,-3,-2),dp[3]要以7结尾那么以7结尾的子序列最大和就是8(6,-3,-2,7)。现在我们开始细细品一下上面这个递推式,求dp[i]的时候是不是有两种可能,要么就是像上面的dp[3]一样,dp[2]求出来是1了,再加上自己array[3]是最大的,那么还有一种可能就是说如果dp[2]我求出来是-100,那如果我也是dp[2]+array[3]的话是-93, 这时候dp[2]反而是累赘,最大就是自己(因为前面定义了必须以i为结尾,也就说必须以7结尾)状态方程式: max( dp[ i ] ) = getMax( max( dp[ i -1 ] ) + arr[ i ] ,arr[ i ] )
#include <iostream>
#include<vector>
using namespace std;
int GetMax(int a, int b) //得到两个数的最大值
{
return (a) > (b) ? (a) : (b);
}
int main(){
int size;
cin >> size;
vector<int> nums(size);
for(size_t i = 0; i < size; ++i)
cin >> nums[i];
int Sum = nums[0]; //临时最大值
int MAX = nums[0]; //比较之后的最大值
for (int i = 1; i < size; i++)
{
Sum = GetMax(Sum + nums[i], nums[i]); //状态方程
if (Sum >= MAX)
MAX = Sum;
//下面的代码具有同等的效果
/*
//相当于当Sum + a[i] < a[i]时,就从i处开始重新计算字串了。
if(Sum + a[i] > a[i])
Sum = Sum + a[i];
else
Sum = a[i];
if (Sum >= MAX)
MAX = Sum;
*/
}
cout << MAX << endl;
return 0;
}