MOS的功耗计算-半桥的功耗
之前在跟同事罗帅讨论驱动器的热损耗,学习了一下,找的一篇TI的文章对半桥的功耗计算。
文章:
Application Report
Calculating Power Dissipation for a H-Bridge or Half Bridge Driver
摘要:
在为电机应用或具有电感特性的负载选择集成 H 桥或半桥驱动器时,必须考虑由于负载电流和输出的 PWM 开关以进行电流调节而导致的驱动器功耗。 器件上消耗的功率会使器件的结温超过环境温度,具体取决于热阻抗。 热阻取决于 IC 的特性(封装、芯片尺寸等)和 PCB 设计,这通常是给定驱动器提供多少电流的限制因素。 要计算给定应用中的最大允许电流,需要估算电机驱动器的总功耗。 本应用报告展示了如何估算功率 FET 和整个器件本身在每种情况下的功耗。
1 集成驱动器中的功耗来源
驱动器 IC 中的功率 FET 有两个基本的功耗来源。
1.1 导通损耗
每个 FET 的导通损耗由于其导通电阻而产生的功耗由下式给出:
P
R
O
N
[
W
]
=
R
O
N
×
I
L
2
P_{RON}[W]= R_{ON} \times I^2_L
PRON[W]=RON×IL2
-
R O N R_{ON} RON=FET 导通电阻[ohm]
-
I L I_L IL = 负载电流[A]
请注意, R O N R_{ON} RON 随温度升高而增加。 因此,随着设备升温,功耗也会增加。 在计算总器件功耗时必须考虑这一点。 通常,RON 在 150 摄氏度时的值大约是 25 摄氏度时的室温值的两倍。
1.2 开关损耗
与基于 PWM 的电流调节相关的开关损耗导致的功耗可以用以下表达式来近似:
- 上升沿和下降沿期间由于输出压摆引起的功耗由下式给出:
P S W 1 [ W ] = ( 0.5 × V M × I L × V M / S R r i s e × f P W M ) + ( 0.5 × V M × I L × V M / S R f a l l × f P W M ) P_{SW1}[W]=(0.5 \times V_M \times I_L \times V_M / SR_{rise}\times f_{PWM}) + (0.5 \times V_M \times I_L \times V_M / SR_{fall}\times f_{PWM}) PSW1[W]=(0.5×VM×IL×VM/SRrise×fPWM)+(0.5×VM×IL×VM/SRfall×fPWM)
- f P W M f_{PWM} fPWM = PWM 开关频率 [Hz]
- V M V_{M} VM = 驱动器电源电压 [V]
- I L I_L IL = 负载电流 [A]
- $SR_{rise} $ = 上升期间的输出电压转换率 [V/sec]
- $SR_{fall} $ = 下降期间的输出电压转换率 [V/sec]
输出压摆率是 EM(电磁)性能和器件功耗之间的平衡。
- 由于开关 FET 之间的死区时间导致的功耗由下式给出:
P S W 2 [ W ] = ( V D × I L × t D E A D r i s e × f P W M ) + ( V D × I L × t D E A D f a l l × f P W M ) P_{SW2}[W]=(V_D \times I_L \times tDEAD_{rise} \times f_{PWM}) + (V_D \times I_L \times tDEAD_{fall} \times f_{PWM}) PSW2[W]=(VD×IL×tDEADrise×fPWM)+(VD×IL×tDEADfall×fPWM)
- f P W M f_{PWM} fPWM = PWM 开关频率 [Hz]
- V D V_{D} VD = FET 体二极管正向偏置电压 [V]
- I L I_L IL = 负载电流 [A]
- $tDEAD_{rise} $ = 上升过程中的死区时间 [sec]
- $tDEAD_{fall} $ = 下降过程中的死区时间 [sec]
死区时间对于降低开关功率 FET 之间的任何电流直通风险是必要的。 集成 FET 驱动器通常具有基于反馈的自定时 FET 开关序列,以确保尽可能小的死区时间,同时避免任何击穿电流。
- 在再循环路径中 FET 导通期间由于 OUTPUT 摆动导致的功耗由下式给出:
P S W 1 [ W ] = ( 0.5 × V D × I L × V D / S R r i s e × f P W M ) + ( 0.5 × V D × I L × V D / S R f a l l × f P W M ) P_{SW1}[W]=(0.5 \times V_D \times I_L \times V_D / SR_{rise}\times f_{PWM}) + (0.5 \times V_D \times I_L \times V_D / SR_{fall}\times f_{PWM}) PSW1[W]=(0.5×VD×IL×VD/SRrise×fPWM)+(0.5×VD×IL×VD/SRfall×fPWM)
这种耗散通常不被考虑,因为它非常微不足道
- 由于开关 FET 的反向恢复损耗也会产生功率耗散。 这是由于典型大功率 FET ( R D S O N R_{DSON} RDSON< ~100 mΩ) 的正向偏置体二极管的电流方向发生变化而发生的。 这些损耗通常会限制较高压摆率(> 25 V/μsec)下的功耗节省。 这种耗散通常也不被考虑,因为它非常微不足道。
1.3 器件电流消耗
器件电流消耗引起的功耗,由下式给出
P
I
V
M
[
W
]
=
V
M
×
I
V
M
P_{IVM}[W]=V_M \times I_{VM}
PIVM[W]=VM×IVM
- V M V_M VM = 驱动器电源电压 [V]
- I V M I_{VM} IVM = 设备工作电源电流 [A]
考虑到 I V M I_{VM} IVM 通常约为 5 - 10 mA,这种耗散通常不被考虑,因为它非常微不足道。
1.4 稳压器ldo消耗
一些驱动器设备具有可用的外部 LDO 稳压器输出,用于提供一些参考电流或为外部负载供电的电流。 由于该外部负载电流而产生的功耗由下式给出
P
L
D
O
[
W
]
=
(
V
M
−
V
L
D
O
)
×
I
L
D
O
P_{LDO}[W]=(V_M - V_{LDO}) \times I_{LDO}
PLDO[W]=(VM−VLDO)×ILDO
这种耗散通常不被考虑,因为它非常微不足道。
总结
总之,总功耗由下式给出:
P
T
O
T
=
P
R
O
N
+
P
S
W
1
+
P
S
W
2
+
P
S
W
3
+
P
I
V
M
+
P
L
D
O
P_{TOT}= P_{RON} + P_{SW1} + P_{SW2} +P_{SW3}+P_{IVM}+P_{LDO}
PTOT=PRON+PSW1+PSW2+PSW3+PIVM+PLDO
通常,这可以近似为三个来源,由下式给出:
P
T
O
T
=
(
P
R
O
N
+
P
S
W
1
+
P
S
W
2
)
P_{TOT}= (P_{RON} + P_{SW1} + P_{SW2})
PTOT=(PRON+PSW1+PSW2)
下一小节根据应用配置(使用高侧或低侧再循环的 H 桥或半桥驱动器)显示每个功率 FET 中用于传导和开关损耗的功率耗散。
半桥
低侧循环的半桥
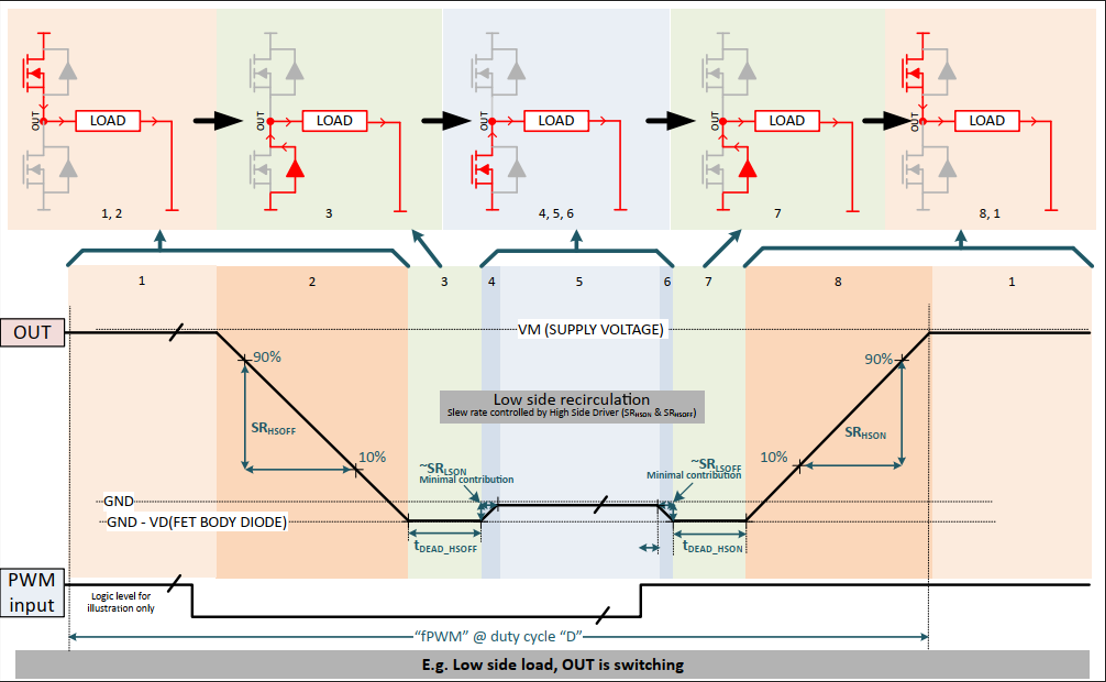
图 1-4 显示了 PWM 调节中半桥在 HS - 负载(区域 #1)和 LS - 负载(区域 #5)与其他转换(上升沿和区域 # 的区域 #2、3 和 4)之间的开关序列 6、7 和 8 用于下降沿)。 每个 FET 的功耗如下:
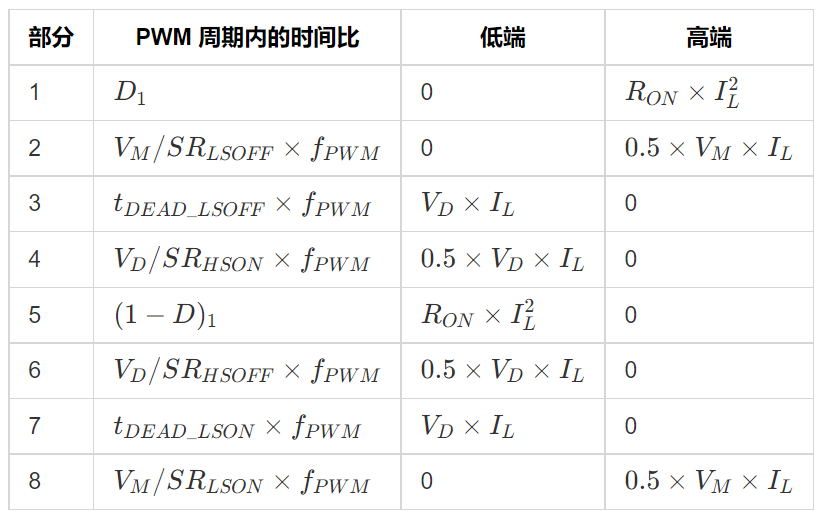
表格中:
- R O N R_{ON} RON=FET 导通电阻[ohm]
- f P W M f_{PWM} fPWM = PWM 开关频率 [Hz]
- V M V_M VM = 驱动器电源电压 [V]
- I L I_L IL = 负载电流[A]
- D = PWM 占空比介于 0 和 1 之间
- $SR_{HSOFF} $ = HS关闭时上升期间的输出电压转换速率 [V/sec]
- $SR_{HSON} $ = HS 开启时下降期间的输出电压转换速率 [V/sec]
- V D V_{D} VD = FET 体二极管正向偏置电压 [V]
- t D E A D _ L S O N t_{DEAD\_LSON} tDEAD_LSON = HS 关闭后的死区时间 [秒]
- $t_{DEAD_LSOFF} $ = HS 开启前的死区时间 [秒]
- $SR_{LSON} $ = LS 开启时上升期间的输出电压转换率 [V/sec]
- $SR_{LSOFF} $ = LS 关闭时下降期间的输出电压转换率 [V/sec]
如果我们假设 #4 和 #6 区域的功耗可以忽略不计,上升沿和下降沿的压摆率匹配,死区时间相等,则每个 FET 的功耗可以近似如下:
P
L
S
=
[
R
O
N
×
I
L
2
×
(
1
−
D
)
]
+
[
2
×
V
D
×
I
L
×
t
D
E
A
D
×
f
P
W
M
]
P_{LS} = [R_{ON} \times I^2_L \times (1-D)] + [2 \times V_D \times I_L \times t_{DEAD} \times f_{PWM}]
PLS=[RON×IL2×(1−D)]+[2×VD×IL×tDEAD×fPWM]
P
H
S
=
[
R
O
N
×
I
L
2
×
D
]
+
[
V
M
×
I
L
×
(
V
M
/
S
R
)
×
f
P
W
M
]
P_{HS} = [R_{ON} \times I^2_L \times D] + [V_M \times I_L \times (V_M /SR) \times f_{PWM}]
PHS=[RON×IL2×D]+[VM×IL×(VM/SR)×fPWM]
与 H 桥驱动器相比,由于传导损耗导致的功耗大约减少了一半,但开关损耗保持不变。
高端侧循环的半桥也是一样的
示例计算
- $R_{ON} $ = 100mΩ
- f P W M f_{PWM} fPWM = 20 KHz
- $V_M $ = 13.5 V
- $I_L $ = 1A
- $D $ = 50%
- $SR_{HSOFF} $ = 13.5 V/us
- $SR_{HSON} $ = 13.5 V/us
- V D V_{D} VD = 1V
- t D E A D _ L S O N t_{DEAD\_LSON} tDEAD_LSON = 100ns
- $t_{DEAD_LSOFF} $ = 100ns
- $SR_{LSON} $ = 13.5 V/us
- $SR_{LSOFF} $ = 13.5 V/us
| 部分 | PWM 周期内的时间比 | 低端 | 高端 |
|---|---|---|---|
| 1 | 50% | 0 | 100 m Ω × 1 2 A 100m \varOmega \times 1^2 A 100mΩ×12A |
| 2 | 13.5V / 13.5V/us x 20KHz | 0 | 0.5 x 13.5V x 1A |
| 3 | 100ns x 20kHz | 1V x 1A | 0 |
| 4 | 13.5V / 13.5V/us x 20KHz | 0.5 x 1V x 1A | 0 |
| 5 | (1-50%) | 100 m Ω × 1 2 A 100m \varOmega \times 1^2 A 100mΩ×12A | 0 |
| 6 | 1V / 13.5V/us x 20KHz | 0.5 x 1V x 1A | 0 |
| 7 | 100ns x 20kHz | 1V x 1A | 0 |
| 8 | 13.5V / 13.5V/us x 20KHz | 0 | 0.5 x 13.5V x 1A |
P L S = [ 100 m Ω × 1 2 A × ( 1 − 0.5 ) ] + [ 2 × 1 V × 1 A × 100 n s × 20 K h z ] = 0.054 W P_{LS} = [100m \varOmega \times 1^2 A \times(1-0.5)] + [2 \times 1V \times 1A \times 100ns \times 20Khz] = 0.054W PLS=[100mΩ×12A×(1−0.5)]+[2×1V×1A×100ns×20Khz]=0.054W
P L S = [ 100 m Ω × 1 2 A × 0.5 ] + [ 13.5 V × 1 A × 13.5 V / 13.5 V / u s × 20 K H z ] = 0.32 W P_{LS} = [100m \varOmega \times 1^2 A \times 0.5] + [ 13.5V \times 1A \times 13.5V / 13.5V/us \times 20KHz] = 0.32 W PLS=[100mΩ×12A×0.5]+[13.5V×1A×13.5V/13.5V/us×20KHz]=0.32W
P T O T = 0.054 + 0.32 = 0.374 W P_{TOT} = 0.054+0.32 = 0.374 W PTOT=0.054+0.32=0.374W
简单的总结,主要的两部分损耗还是在导通损耗和开关损耗上。
- 影响导通损耗的主要是导通的电阻 R O N R_{ON} RON,可以选择导通电阻小一些的mos,减少发热。
- 影响开关损耗的主要是电压上升的速度,所以我们更希望,开通关断的更快一些。因为在这个时间里,损耗是I*U。
