【AI面试】BN(Batch Norm)批量归一化
在提到批量归一化的面试问题时候,一般会以以下几种形式提问:
- 为什么要引入BN?
- BN解决了什么问题?
- BN的公式是怎样的?
- BN公式中,有哪些参数是可学的?
- BN中,均值和方差的尺寸shape是什么样子的?
- BN在训练阶段和验证阶段,有什么不同?
本文就围绕上述的问题,展开来说,希望对你有帮助。如果真有,麻烦给个赞👍,支持一波。
后面的内容主要是学习了沐神的视频,进行了一些理解和补充。感兴趣的可以直接去看原视频,视频链接:批量归一化【动手学深度学习v2】
一、批量归一化概念
1.1、为什么要引入批量归一化

我们都知道:
- 数据
forward阶段,从下往上,输入数据,得到结果做预测;backward阶段,损失loss从上往下进行梯度回传; - 梯度在上面会比较大,越往下传播会越小;(n个很小的数相乘,梯度越往后传播,会越小)
- 一次回传,梯度更新,学习率是一样的,就导致越靠近损失部分,模型更新的较快;越靠近数据部分,也就是远离损失部分,模型更新的越慢。
- 进而导致,靠近损失的部分,很快收敛;远离损失的部分,就收敛很慢。
但是呢?
- 越靠近数据的网络呢,学习到的是更具体的特征,比如边缘、纹理等等;越远离数据部分呢,学习到更多抽象的特征。
- 可是,靠近数据部分的模型,学习的慢,远离数据的模型,学习的快;为了使模型整体性能较好,就需要更多次的训练,使各个部分都得到充分的学习。
- 这样,为了使得模型更优,难以训练的底层模型就要不断的在改变;底层的模型一旦发生改变,基于此的更高维度的模型,就需要重新学习,之前学的白学了。
- 模型更新的不一致性,要想得到最优的模型,就需要更多次的迭代,从而导致训练变慢。
那么,问题来了?
我们能不能在学习底层特征的时候,避免顶层特征的剧烈变化?这就是BN批量归一化要解决的问题。
1.2、计算公式

上图展示的就是批量归一化的公式,其中:
B(batch),一个批次的大小xi,一个输入样本x(i+1),xi经过BN后的输出ε,一个比较小的数,例如1e-5,避免分母为0μB,均值,所有相本求和,除以一个批次所有样本个数σB,方差,所有样本,减去均值的平方求和,除以一个批次所有样本个数
然后,利用一个Batch批次的所有样本计算得到的均值和方差,参与到每一个样本的调整中去,使得输入的一个样本xi,经过BN后,得到x(i+1)。其中,γ 和β是BN中唯一两个可学习的参数。
大概的意思就是:通过计算得到了一个均值和方差,但是这个均值和方差可能并不是很适用于这批数据。采用γ 和β进行二次调整到比较合适的区间,加速训练。
1.3、批量归一化该怎么使用呢?

- 作用在全连接层、和卷积层的输出上,激活函数前(
conv\fc\bn是线性的,激活函数是增加非线性的。假设激活函数是Relu,放到BN前面,Relu把数据被拉到了>=0的范围,BN又拉回到0-1的范围,那么激活函数的作用,就大打折扣了) - 作用在全连接层、和卷积层的输入上
BN的缺点:Batch Normalization 的一个缺点是需要较大的 batchsize 才能合理估训练数据的均值和方差(横向计算),这导致内存很可能不够用,同时它也很难应用在训练数据长度不同的 RNN 模型上。
1.4、批量归一化在做什么?

什么是内部协变量转移:
内部协变量偏移(Internal Covariate Shift):是指在深度神经网络的训练过程中,由于每一层的参数都在不断更新,导致每一层输入分布的改变,从而增加了下一层的训练难度。
因为每一层的输入分布的改变,可能需要重新学习适应新的分布的权重,这会增加训练的时间和难度。
这篇论文对BN关于解决内部协变量偏移转移进行了详细的介绍:
Batch Normalization: Accelerating Deep Network Training byReducing Internal Covariate Shift
但是,在后面的研究中,人们发现BN是非常的有效的,但BN并没有引起内部协变量转移。
于是就有了加入噪声的理论。每一次的batch都是一次不一样的数据,所以他的均值和方差也就发生了改变。进一步使得输入的x经过BN后得到新的x,也就引入了噪声。这些随机的干扰噪声,控制模型复杂度,避免了模型过拟合。
与此同时,dropout是对输入的部分,随机的丢弃,也是一种降低模型复杂度的模块。所以,实验表明,BN后没必要增加dropout层,并没有进一步提高准确度。
1.5、BN小结
- 批量归一化固定小批量中的均值和方差,然后学习出适合的平移(乘法)和缩放(加法);
- 可以加速收敛速度(使用很高的学习率,对初始化不太在意),但一般不改变模型精度。
二、推理阶段
BN在训练的时候可以根据Mini-Batch里的若干训练实例样本(x2、x2、x3···)进行激活数值调整。
但是在实际的推理(inference)的过程中,很明显输入就只有一个实例(x1),看不到Mini-Batch其它实例,那么这时候怎么对输入做BN呢?
因为很明显一个实例是没法算实例集合求出的均值和方差的。这可如何是好?
既然没有从Mini-Batch数据里可以得到的统计量,那就想其它办法来获得这个统计量,就是均值和方差。可以用从所有训练实例中获得的统计量来代替Mini-Batch里面m个训练实例获得的均值和方差统计量。
因为:本来就打算用全局的统计量,只是因为计算量等太大所以才会用Mini-Batch这种简化方式的,那么在推理的时候直接用全局统计量即可,也就是在推理阶段,这个BN内的所有参数都是固定的,包括均值、方差、γ 和β四个值。
决定了获得统计量的数据范围,那么接下来的问题是如何获得均值和方差的问题。很简单,因为每次做Mini-Batch训练时,都会有那个Mini-Batch里m个训练实例获得的均值和方差,现在要全局统计量,只要把每个Mini-Batch的均值和方差统计量记住,然后对这些均值和方差求其对应的数学期望即可得出全局统计量,即:
三、代码实现
BN训练和验证阶段的实现代码,大概步骤如下:
- 先是判断是训练,还是验证阶段
- 如果是验证阶段,就简单了,直接带入公式进行更新
- 如果是训练阶段,就要判断是卷积后面的BN,还是全连接后面的BN,根据不同的尺寸,需要计算的均值和方差尺寸也不一样
- 更新全局均值和方差
- 最后对输入X进行更新,得到BN后的值Y,输出
import torch
from torch import nn
def batch_normal(X, gamma, beta, moving_mean, moving_var, eps, momentum):
"""
X: 输入
gamma, beta: 可学习参数
moving_mean, moving_var:均值和方差
eps: 避免除0
momentum:更新动量
"""
# 判断是训练or验证阶段:可以梯度回归就是训练阶段,否则就是验证阶段
if not torch.is_grad_enabled(): # 如果是验证阶段,那就直接用就好了
X_hat = (X-moving_mean) / torch.sqrt(moving_var + eps)
else:
assert len(X.shape) in (2, 4) # 判断一下它是不是接在卷积和全连接的输出数据上,卷积就是(B,C,H,W),
# 全连接就是(B,C*H*W)
if len(X.shape) == 2:
mean = X.mean(dim=0)
var = ((X-mean)**2).mean(dim=0)
else:
# 在channel维度上,将所有的值求均值和方差,包括了batch, 宽和高
mean = X.mean(dim=(0, 2, 3), keepdim=True) # shape:(1, N, 1, 1) 4D
var = ((X-mean)**2).mean(dim=(0, 2, 3), keepdim=True)
X_hat = (X-mean) / torch.sqrt(var + eps)
# 更新全局的 moving_mean和moving_var
moving_mean = momentum * moving_mean + (1-momentum) * mean
moving_var = momentum * moving_var + (1 - momentum) * var
# 输出BN后的值
Y = gamma * X_hat + beta
return Y, moving_mean.data, moving_var.data,
四、其他形式的Normalization
产生一个问题:当限于GPU内存等原因,Batch取不大,只能batchsize=1时是,BN的情况如何处理?
网友答:当batch_size=1,这时候计算的均值和方差,其实并不能代表数据集的分布情况。所以,计算BatchNorm就不能准确估计数据集的均值和方差
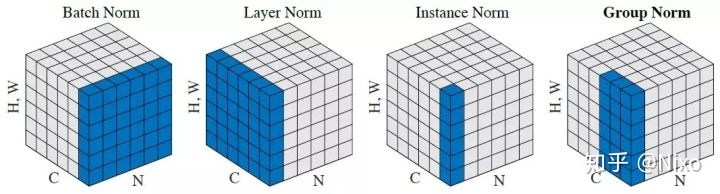
于是,就产生了各种BN的变种,主流的如下:
- BatchNorm:
batch方向做归一化,算N*H*W的均值 - LayerNorm:
channel方向做归一化,算C*H*W的均值 - InstanceNorm:
一个channel内做归一化,算H*W的均值 - GroupNorm: 将
channel方向分group,然后每个group内做归一化,算(C//G)*H*W的均值
BN和GN和低batchsize下,error随着batch size的大小的表现情况,可以发现:
Batch Norm随着batch size变小,error错误在逐渐变大Gropu Norm在改变batch size的时候,error错误变化不大,且在Batch Norm较好的水平
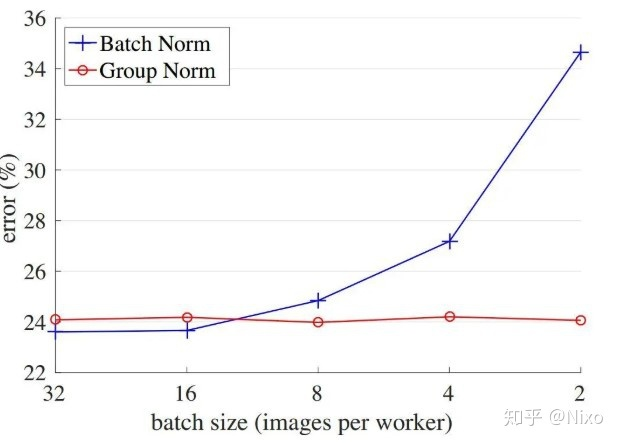
上图来自论文:Group Normalization-Kaiming He大佬参与的作品
下面是一个更加全面的比较,如下:
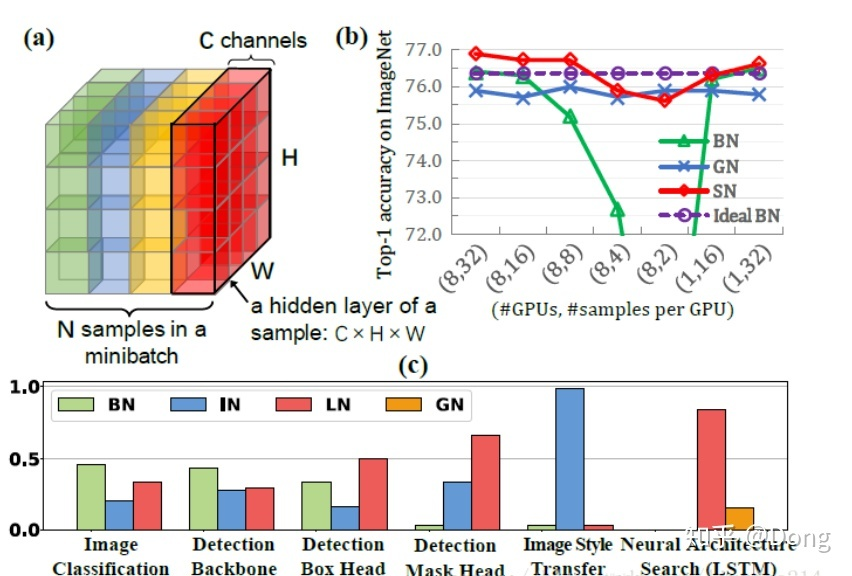
推荐阅读:BN、LN、IN、GN的简介
问题2:BN,GN,IN 为啥有效,分别都用在哪些方面?
答:这个问题可以用在上面这个链接里面找到答案。每一个归一化都有其解决的问题和适用场景。有解决小批量的问题的,有更适用于分割问题的等等。
其他面试题链接:https://zhuanlan.zhihu.com/p/84606026
