计算机底层:循环冗余校验码CRC
计算机底层:循环冗余校验码CRC
信息位+校验位组成循环冗余校验码,也称CRC码。
循环冗余校验码的思想:
通过将信息进行除以某个规定的数,这个数是提前约定好的,并且两边都知道的数。
假设信息是882,约定了除数是7
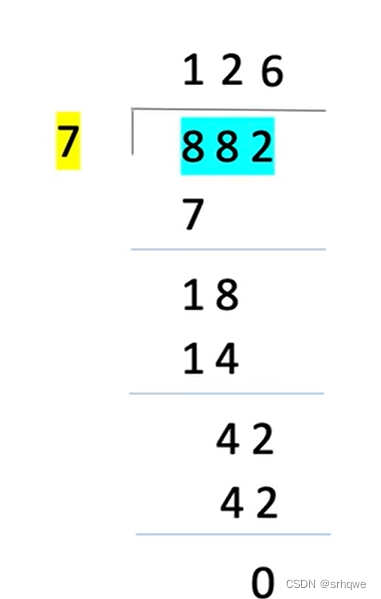
那么为啥是7呢?计算机可以通过逆运算推出来,当找到可以令余数为0的数时,两边计算机就可以约定将这个数作为除数
如果得到余数为0,那么这个信息就是正确的,如果不是0,则是错误的:
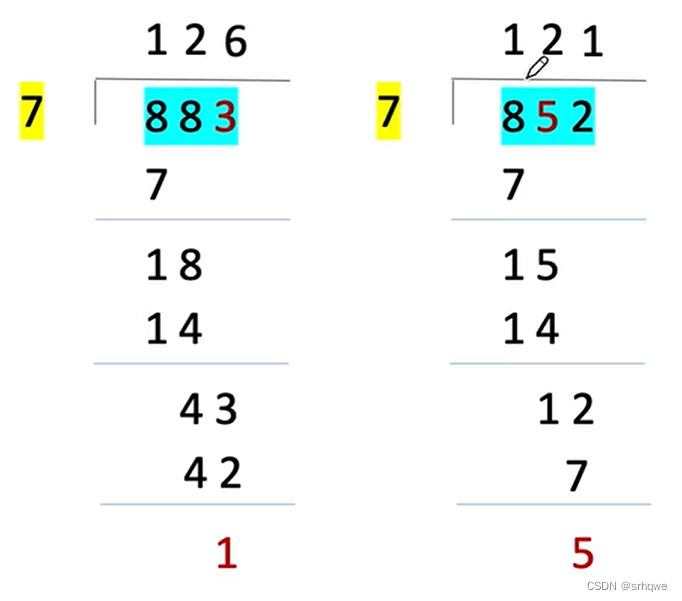
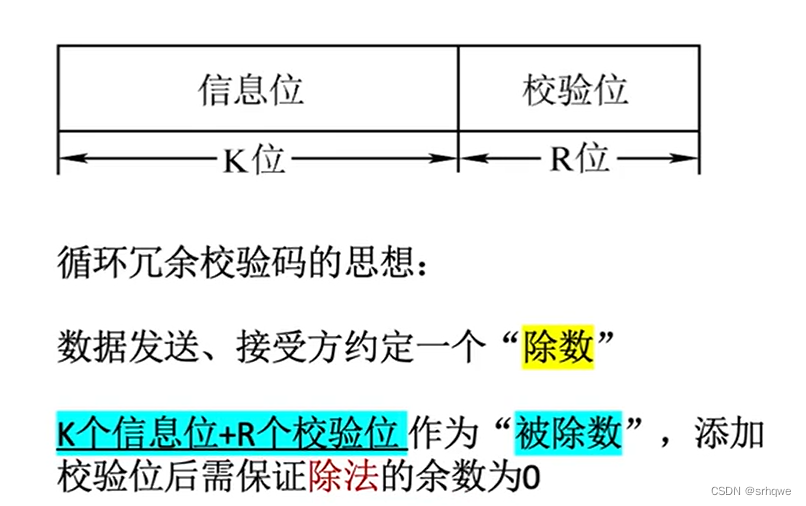
以上是为了方便理解循环冗余校验码,但是并不是真正的循环冗余校验码的过程。切勿将以上认作是循环冗余校验码
但以上的十进制除法的方式,与循环冗余校验码还是很像的。
循环冗余校验码CRC:
用题目理解:p
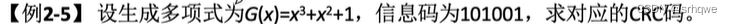
与上面一样的是:会规定一个除数和被除数。
除数:
会通过生成多项式,来规定除数。起始除数是一串二进制码,那图中的生成多显示G(x)怎么是一个函数呢?
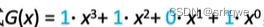
G(x)可以分解成如上图所示,这样就可以得到一串二进制:1101,而这就是真正的生成多项式。
那题目中生成多项式G(x)是如何的来的呢?
计算机想要得到生成多项式,首先需要确定需求,我们是要纠错呢?还是只需要查错呢?因为我们并不了解循环冗余校验码是如何差错或是纠错的,因此可以先看完整篇文章后,再看这里。
如果想要使校验码拥有纠错能力。那么需要设定知道信息位数K,和校验位数R。使得2^R≥K+R+1。这个公式的意思和海明校验码的意思一样:用2^R所能表示的状态数量,能够表示出错位置的数量。其中R的位数是生成多项式所确定位数的-1个位数。这里不太懂也可以看完整篇文章,再看这里。
学到后面其实还会发现,生成多项式表示的位数越多,校验强度其实越高,既然如此就极易消耗cpu和内存。因此计算机规定校验位数量时,会依据计算机的计算能力和存储能力进行判断。
以上内容下面会解释。
除数的作用:
1.用于得到校验位上的校验码。
2.用于对CRC校验码进行校验。
被除数:
被除数包括了两种:
1.信息位作为被除数,即题目中的:101001。信息位作为被除数,是为了得到校验位上的校验码。
2.信息位+校验位即CRC码作为被除数,是为了进行CRC校验码进行校验。
可以看到题目中的要求是得到CRC 码,就是得到校验位。
获取校验位:
想要得到校验位,需要有:1.信息位,2.生成多项式。
信息位是:101001
生成多项式是:1101
得到两个信息后,需要将除数(生成多项式)的位数-1,那么就是n=3(最高次幂),得到的这个数,然后在信息位后添n=3加个0。即:101001000
然后进行除法运算:

得到的余数是n=3个位。
运算方法: 模二除。
只看首位,是1就x1进去:
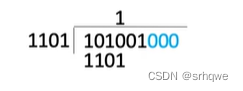
再对1后面的三位010与101进行异或,在得到的结果后面添加信息位的下一个位:
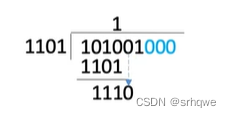
如果遇到第一位是0,那么就x0进去,得到了0000,再进行后三位的异或:

以此类推,最后会得到3bit位的余数,这3位的余数,就是我们添加到信息位后的校验位:

最后得到了CRC码:
到了这里,我们再说说生成多项式:
1.校验位数和生成多项式是有着关系的,生成多项式的最高次幂是校验位的位数。
2.生成多项式位数越多,在得到校验位的计算上,信息位后面需要补更多的0,位数变多了,计算量也就变大了,同时储存它们的空间也需要变大。
3.不及如此,生成多项式位数越多,除数也会变多。因为除数就是生成多项式。
CRC码的校验:
接收方收到发送方的CRC校验码时,需要对CRC校验码进行校验。
生成多项式是接收方和发送方一起规定的,因此都会知道这个生成多项式。
校验方式还是:模二除
还是将生成多项式作为除数,接收的CRC校验码作为被除数。

尝试未出错时的计算:

发现:最后的余数是000,说明信息未发生改变。

尝试发生改变时的计算:

发现:得到了010的余数,不为000说明发生了错误。
CRC码的纠错问题:
根据上图中余数是010,而出错位置也是010。那么余数真的表示出错位置吗?
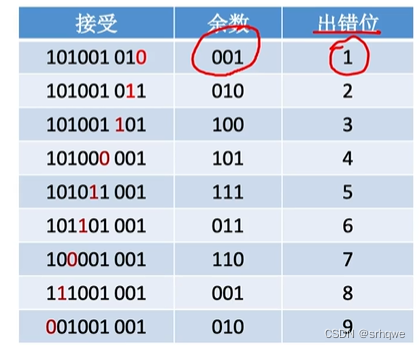
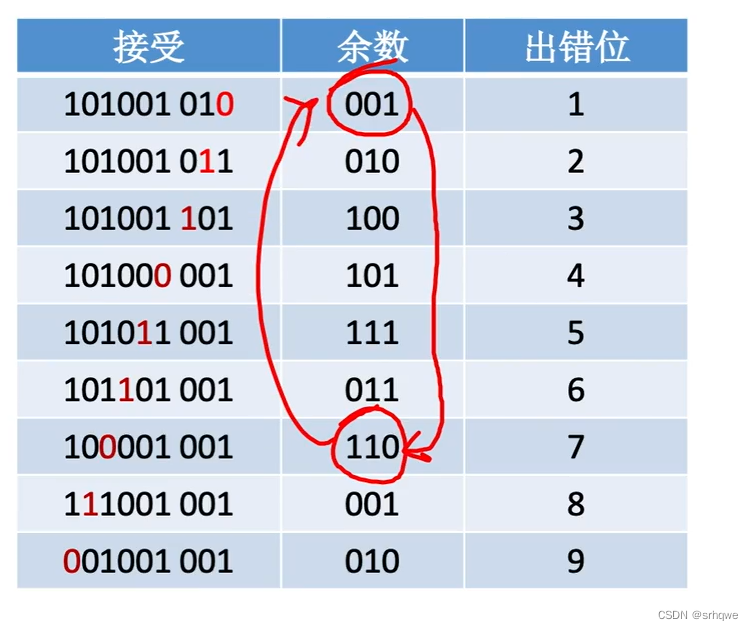
算出每个出错位置,以及对应的余数,得到一个表格:

上图发现余数为001和010的位置有两处。显然在这里余数并不能表示出错位置。
图中用余数表示出错位置,余数只有3位,只有2^3=8种状态,其中000是其中的一种用来表示正确状态,其余7种表示错误状态。
所以我们知道,余数3位只能表示7种错误位置。也就是到图中第七位的错误为止。
我们会发现这里不能纠错的原因是:第八位和第九位的存在,导致只有3位的余数,不够表示错误位置。
那我们如果减少信息位,让CRC码只有7位,那么余数的7种状态就完全可以一一对应,使得拥有纠错的能力。
减少信息位例题:

信息位只有4位,生成多项式还是1101,得到的CRC码只有7位。
此时再看图:
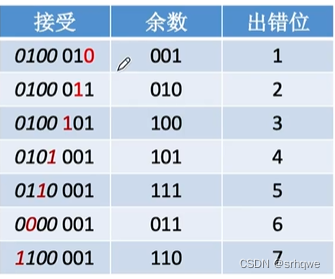
该信息位置与余数一一对应,这样当我们知道余数时,就可以知道错误位置再哪了。
以上是减少信息位,显然现实中,减少信息位肯定是不可能的。发送的信息是人规定死的。机器不能减少。
因此机器会选择增多余数,这样余数增多,所能表示的位数就越多。虽然余数和校验位位数是一样的,但是校验位数的增多绝对赶不上余数表示错误位置的数量。
巩固记忆:生成多项式最高次幂,可以表示:1.计算校验位时,需要再信息位添加0的个数。2.校验位个数。3.进行校验所得到的余数。
生成多项式无论在获取校验码或是进行校验时,都作为除数。
比如:0100010余数有3bit,表示7种错误位置。刚好全部可以表示
01000101余数有4bit,可以表示2^4=16种状态,还有8种状态冗余
010001010余数有5bit,可以表示2^5=32种状态,还有23中状态冗余。
由此,我们就可以知道,余数越多纠错能力就越强。
回到生成多项式:
我们知道余数和生成多项式有关,进而说明了生成多项式越多位,就能够进行更多的纠错,所以文章开头说生成多项式的时候说:按需求而定,是想要纠错呢?还是单纯检错?
到此可以回看上面的生成多项式,这样你可以完全明白生成多项式这个东西

学完循环冗余校验码,更需要知道它的引用领域:
循环冗余校验码通常只会用在计算机网络当中,且在OSI七层模型架构中的数据链路层。
而且,一般不会用到它的纠错能力,只会用到检错能力。
知识回顾:
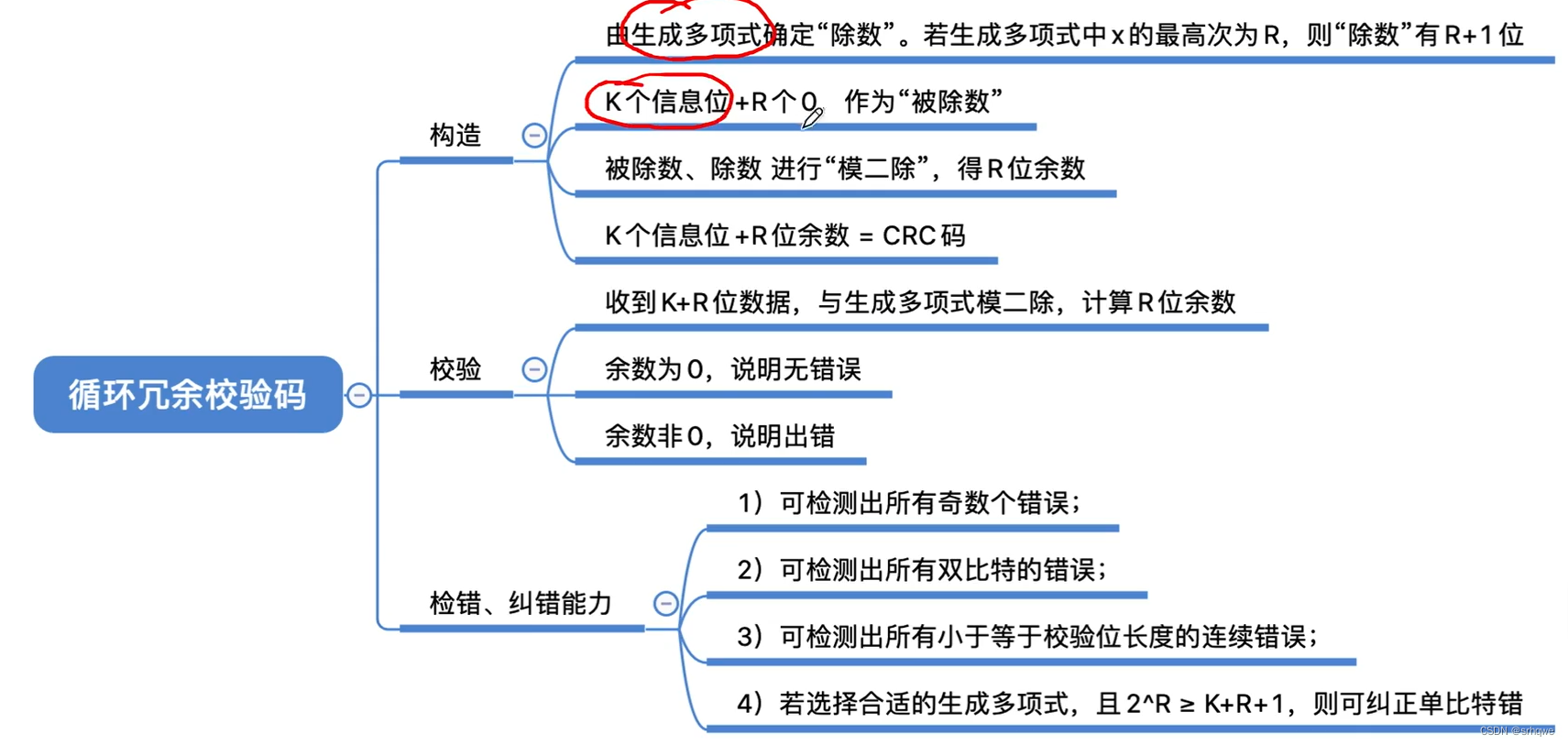
循环冗余校验码的由来(只是补充,不学也行):

将余数作为被除数,生成多项式作为除数。
在余数后面补一个0,保证余数个数和生成多项式位数一样。

由此进行模二除的运算:
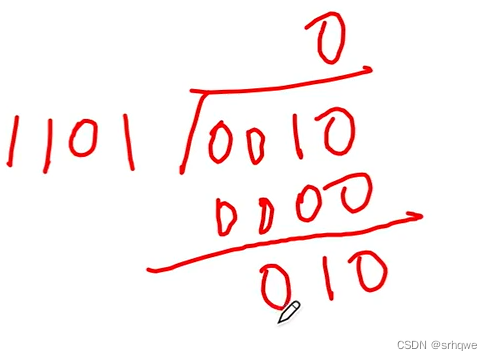
会发现:得到的余数010是CRC码第二位错误时的余数。继续往下:
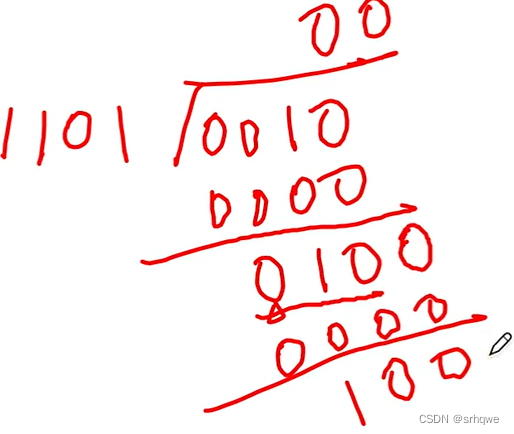
发现余数又是下一个位置出错的余数。继续往下:

发现101又是下一个
当你继续算下去会发现会算到110,然后继续算时又会回到001,就这样一直往复,一直循环
因此就叫做:循环冗余校验码