当前位置：首页 > article >正文

【机器学习算法实践】GBDT提升树，集成学习boosting方法，可分类课可回归，CART树是基础，调参是重点

article 2024/12/23 20:43:28

Adaboost是利用前一轮迭代弱学习器的误差率来更新训练集的权重，这样一轮轮的迭代下去。虽然GBDT也是Boosting家族的成员，但是却和Adaboost【机器学习算法实践】AdaBoost是典型的Boosting算法，加法模型多个弱分类器流水线式的提升精度，更关注那些难处理的数据_羞儿的博客-CSDN博客有很大的不同。GBDT也是迭代，使用了前向分布算法，但是弱学习器限定了只能使用CART回归树模型，同时GBDT是基于残差学习的算法，没有AdaBoost中的样本权重的概念。GBDT有很多简称，有GBT（Gradient Boosting Tree）、 GTB（Gradient Tree Boosting ）、GBRT（Gradient Boosting Regression Tree）梯度提升回归树、MART(Multiple Additive Regression Tree)多决策回归树、Tree Net决策树网络，其实都是指的同一种算法
假设在GBDT的迭代中，前一轮迭代得到的强学习器是 $f_{t-1}(x)$ , 损失函数是 $L(y,f_{t-1}(x)$ , 则本轮迭代的目标是找到一个CART回归树模型的弱学习器，让本轮的损失损失 $L(y,f_t(x))=L(y,f_{t-1}(x)+h_t(x))$ 最小。也就是说，本轮迭代找到决策树，要让样本的损失尽量变得更小。GBDT采用了多模型集成的策略，针对残差进行拟合，进而降低模型的偏差和方差。
集成模型（Ensemble Model）不是一种具体的模型，而是一种模型框架，它采用的是“三个臭皮匠顶个诸葛亮”的思想。集成模型的一般做法是，将若干个模型(俗称“弱学习器”, weak learner，基础模型，base model)按照一定的策略组合起来，共同完成一个任务——特定的组合策略，可以帮助集成模型降低预测的偏差或者方差。常见的集成策略有bagging、stacking、boosting。GBDT(梯度提升决策树)——来由、原理和python实现 - 知乎 (zhihu.com)
- bagging模型会把(相同的)若干基础模型简单的“装起来”——基础模型独立训练，然后将它们的输出用特定的规则综合(比如求平均值)起来，形成最后的预测值。在回归类任务中，bagging模型假设各个基础模型的预测值“错落有致”，分布在真实值的周围——把这些预测值平均一下，就可以稳定地得到一个比较准确的预测值;而在分类任务中，bagging模型认为“每一个基础模型都判断错误”发生的概率是比较低的，基础模型中的相当一部分会做出正确的判断，因此可以基于大家的投票结果来选择最终类别。
- Stacking模型比bagging模型更进2步：(a)允许使用不同类型的模型作为base model；（b）使用一个机器学习模型把所有base model的输出汇总起来，形成最终的输出。（b）所述的模型被称为“元模型”。在训练的时候，base model们直接基于训练数据独立训练，而元模型会以它们的输出为输入数据、以训练数据的输出为输出数据进行训练。Stacking模型认为，各个基础模型的能力不一，投票的时候不能给以相同的权重，而需要用一个“元模型”对各个基础模型的预测值进行加权。
- Boosting模型采用另一种形式，把基础模型组合起来——串联。这类模型的思想是，既然一个基础模型可以做出不完美的预测，那么我们可以用第二的基础模型，把“不完美的部分”补上。我们可以使用很多的基础模型，不断地对“不完美的部分”进行完善，以得到效果足够好的集成模型。Boosting的策略非常多，以GBDT为例，它会用第K个CART拟合前k-1个CART留下的残差，从而不断的缩小整个模型的误差。
提升树模型
- 提升方法实际采用加法模型（即基函数的线性组合）与前向分布算法。以决策树为基函数的提升方法称为提升树（boosting tree）。对分类问题决策树是二叉分类树，对回归问题决策树是二叉回归树。只有一个条件的基本分类器可以看做是由一个根结点直接连接两个叶结点简单决策树，即所谓的决策树桩（decision stump）。提升树模型可以表示为决策树的加法模型： $f_M(x)=\sum_{m=1}^MT(x;\Theta_m)$ 。其中， $\Theta_m$ 表示决策树； $T(x;\Theta_m)$ 为决策树的参数； M 为树的个数。提升树中树之间没有权重，或者说它们的权重都是一样的，树之间是独立的，训练样本之间也没有权重的概念，这是提升树和随机森林、AdaBoost之间的区别。
提升树模型每一次的提升都是靠上次的预测结果与训练数据的label值差值作为新的训练数据进行重新训练，GDBT则是将残差计算替换成了损失函数的梯度方向，将上一次的预测结果带入梯度中求出本轮的训练数据，也就是说这两种模型在生成新的训练数据时采用了不同的方法。在使用平方误差损失函数和指数损失函数时，提升树的残差求解比较简单，但是在使用一般的损失误差函数时，残差求解起来不是那么容易，所以就使用损失函数的负梯度在当前模型的值作为回归问题中残差的近似值。
GBDT主要的优缺点有：
- 可以灵活处理各种类型的数据，包括连续值和离散值。在相对少的调参时间情况下，预测的准备率也可以比较高。这个是相对SVM来说的。使用一些健壮的损失函数，对异常值的鲁棒性非常强。比如 Huber损失函数和Quantile损失函数。
- 由于弱学习器之间存在依赖关系，难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行。
GBDT回归算法梯度提升树(GBDT)原理小结 - 刘建平Pinard - 博客园 (cnblogs.com)
- 输入是训练集样本 $T=\{(x_1,y_1),(x_2,y_2),...(x_m,y_m)\}$ ，最大迭代次数T, 损失函数L。
- 输出是强学习器f(x)。
  - 初始化弱学习器 $f_0(x)=\underbrace{argmin}_{c}\sum^m_{i=1}L(y_i,c)$ ；
  - 对迭代轮数t=1,2,…T有：
    - 对样本i=1,2，…m，计算负梯度 $r_{ti}=-[\frac{\delta L(y_i,f(x_i))}{\delta f(x_i)}]_{f(x)=f_{t-1}(x)}$ ，
    - 利用 $x_i,r_{ti})(i=1,2,..m)$ , 拟合一颗CART回归树,得到第 t 颗回归树，其对应的叶子节点区域为 $R_{tj},j=1,2,...,J$ 。其中 J 为回归树 t 的叶子节点的个数。
    - 对叶子区域 $j = 1, 2, .. J$ ,计算最佳拟合值 , $c_{tj}=\underbrace{argmin}_c\sum_{x_i\in R_{tj}}L(y_i,f_{t-1}(x_i)+c)$ ;
    - 更新强学习器 $f_t(x)=f_{t-1}(x)+\sum_{j=1}^Jc_{tj}I(x\in R_{tj})$ 。
  - 得到强学习器f(x)的表达式 $f(x)=f_T(x)=f_0(x)+\sum_{t=1}^T\sum_{j=1}^Jc_{tj}I(x\in R_{tj})$ 。
GBDT分类算法
- GBDT的分类算法从思想上和GBDT的回归算法没有区别，但是由于样本输出不是连续的值，而是离散的类别，导致我们无法直接从输出类别去拟合类别输出的误差。为了解决这个问题，主要有两个方法，一个是用指数损失函数，此时GBDT退化为Adaboost算法。另一种方法是用类似于逻辑回归的对数似然损失函数的方法。也就是说，我们用的是类别的预测概率值和真实概率值的差来拟合损失。
- 二元GBDT分类算法
  - 对于二元GBDT，如果用类似于逻辑回归的对数似然损失函数，则损失函数为： $L (y, f (x)) = l o g (1 + e x p (- y f (x)))$ ,其中y∈{−1,+1}。则此时的负梯度误差为 $r_{tj}=-[\frac{\delta L(y,f(x_i))}{\delta f(x_i)}]_{f(x)=f_{t-1}(x)}=\frac{y_i}{1+exp(y_if(x_i))}$ 。
  - 对于生成的决策树，我们各个叶子节点的最佳负梯度拟合值为 $c_{tj}=\underbrace{argmin}_c\sum_{x_i\in R_{tj}}log(1+exp(-y_i(f_{t-1}(x_i)+c)))$ 。由于上式比较难优化，我们一般使用近似值代替 $c_{tj}=\sum_{x_i\in R_{tj}}r_{tj}/\sum_{x_i\in R_{tj}}|x_{ti}|(1-|r_{ti}|)$ 。
  - 除了负梯度计算和叶子节点的最佳负梯度拟合的线性搜索，二元GBDT分类和GBDT回归算法过程相同。
- 多元GBDT分类算法
  - 多元GBDT要比二元GBDT复杂一些，对应的是多元逻辑回归和二元逻辑回归的复杂度差别。假设类别数为K，则此时我们的对数似然损失函数为： $L(y,f(x))=-\sum_{k=1}^Ky_klogp_k(x)$ ,其中如果样本输出类别为k，则 $y_k=1$ 。第k类的概率 $p_k(x)$ 的表达式为： $p_k(x)=exp(f_k(x))/\sum_{i=1}^Kexp(f_l(x))$ 。
  - 集合上两式，我们可以计算出第t轮的第i个样本对应类别l的负梯度误差为 $r_{til}=-[\frac{\delta L(y_i,f(x_i))}{\delta f(x_i)}]_{f_k(x)=f_{l,t-1}(x)}=y_{il}-p_{l,t-1}(x_i)$ 。观察上式可以看出，其实这里的误差就是样本i对应类别l的真实概率和t−1轮预测概率的差值。
  - 对于生成的决策树，我们各个叶子节点的最佳负梯度拟合值为 $c_{tjl}=\underbrace{argmin}_{c_{jl}}\sum_{i=0}^m\sum_{k=1}^KL(y_k,f_{t-1,l}(x)+\sum_{j=0}^Jc_{jl}I(x_i\in R_{tjl}))$ 。　由于上式比较难优化，我们一般使用近似值代替 $c_{tjl}=\frac{K-1}{K}\frac{\sum_{x_i\in R_{tjl}}r_{til}}{\sum_{x_i\in R_{tjl}}|r_{til}|(1-|r_{til}|)}$ 。
  - 除了负梯度计算和叶子节点的最佳负梯度拟合的线性搜索，多元GBDT分类和二元GBDT分类以及GBDT回归算法过程相同。
GBDT常用损失函数
- 对于分类算法，其损失函数一般有对数损失函数和指数损失函数两种:
  - 如果是指数损失函数，则损失函数表达式为 $L (y, f (x)) = e x p (- y f (x))$ ,其负梯度计算和叶子节点的最佳负梯度拟合。
  - 果是对数损失函数，分为二元分类和多元分类两种。
- 对于回归算法，常用损失函数有如下4种:
  - 均方差，这个是最常见的回归损失函数了 $L(y,f(x))=(y-f(x))^2$ 。
  - 绝对损失， $L (y, f (x)) = ∣ y - f (x) ∣$ 。对应负梯度误差为： $sign(y_i-f(x))$ 。
  - Huber损失，它是均方差和绝对损失的折衷产物，对于远离中心的异常点，采用绝对损失，而中心附近的点采用均方差。这个界限一般用分位数点度量。损失函数如下： $\begin{cases} \frac{1}{2}(y-f(x))^2 &{if ~~~~|y-f(x)\leq\delta|}\\ \delta(|y-f(x)|-\frac\delta2) &{if ~~~~|y-f(x)>\delta|}\\ \end{cases}$ 。对应的负梯度误差为： $r(y_i,f(x_i)) = \begin{cases} (y_i-f(x_i)) &{if ~~~~|y-f(x)\leq\delta|}\\ \delta sign(y_i-f(x_i)) &{if ~~~~|y-f(x)>\delta|}\ \end{cases}$ 。
  - 分位数损失。它对应的是分位数回归的损失函数，表达式为 $L(y,f(x))=\sum_{y\geq f(x)}\theta|y-f(x)|+\sum_{y<f(x)}(1-\theta)|y-f(x)|$ 。其中θ为分位数，需要我们在回归前指定。对应的负梯度误差为： $r(y_i.f(x_i))=\theta ~~if~~y_i\geq f(x_i)~~else~~\theta-1$ 。
  - 对于Huber损失和分位数损失，主要用于健壮回归，也就是减少异常点对损失函数的影响。
GBDT的正则化，GBDT的正则化主要有三种方式。
- 第一种是和Adaboost类似的正则化项，即步长(learning rate)。定义为ν,对于前面的弱学习器的迭代 $f_k(x)=f_{k-1}(x)+h_k(x)$ 。如果我们加上了正则化项，则有 $f_k(x)=f_{k-1}(x)+vh_k(x)$ 。ν的取值范围为0<ν≤1。对于同样的训练集学习效果，较小的ν意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。
- 第二种正则化的方式是通过子采样比例（subsample）。取值为(0,1]。注意这里的子采样和随机森林不一样，随机森林使用的是放回抽样，而这里是不放回抽样。如果取值为1，则全部样本都使用，等于没有使用子采样。如果取值小于1，则只有一部分样本会去做GBDT的决策树拟合。选择小于1的比例可以减少方差，即防止过拟合，但是会增加样本拟合的偏差，因此取值不能太低。推荐在[0.5, 0.8]之间。使用了子采样的GBDT有时也称作随机梯度提升树(Stochastic Gradient Boosting Tree, SGBT)。由于使用了子采样，程序可以通过采样分发到不同的任务去做boosting的迭代过程，最后形成新树，从而减少弱学习器难以并行学习的弱点。
- 第三种是对于弱学习器即CART回归树进行正则化剪枝。(2条消息) 【机器学习算法复现】决策树，树形结构解决属性选择问题，一种可回归可分类的有监督学习算法_羞儿的博客-CSDN博客
scikit-learn GBDT类库概述scikit-learn 梯度提升树(GBDT)调参小结 - 刘建平Pinard - 博客园 (cnblogs.com)
- 在scikit-learn中，GradientBoostingClassifier为GBDT的分类类，而GradientBoostingRegressor为GBDT的回归类。两者的参数类型完全相同，当然有些参数比如损失函数loss的可选择项并不相同。这些参数中，类似于Adaboost，我们把重要参数分为两类，第一类是Boosting框架的重要参数，第二类是弱学习器即CART回归树的重要参数。
- GBDT类库boosting框架参数
  - n_estimators: 也就是弱学习器的最大迭代次数，或者说最大的弱学习器的个数。一般来说n_estimators太小，容易欠拟合，n_estimators太大，又容易过拟合，一般选择一个适中的数值。默认是100。在实际调参的过程中，我们常常将n_estimators和下面介绍的参数learning_rate一起考虑。
  - learning_rate: 即每个弱学习器的权重缩减系数ν，也称作步长，在原理篇的正则化章节我们也讲到了，加上了正则化项，我们的强学习器的迭代公式为 $f_k(x)=f_{k−1}(x)+νh_k(x)$ 。ν的取值范围为0<ν≤1。对于同样的训练集拟合效果，较小的ν意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。所以这两个参数n_estimators和learning_rate要一起调参。一般来说，可以从一个小一点的ν开始调参，默认是1。
  - subsample: 即我们在原理部分讲到的子采样，取值为(0,1]。注意这里的子采样和随机森林不一样，随机森林使用的是放回抽样，而这里是不放回抽样。如果取值为1，则全部样本都使用，等于没有使用子采样。如果取值小于1，则只有一部分样本会去做GBDT的决策树拟合。选择小于1的比例可以减少方差，即防止过拟合，但是会增加样本拟合的偏差，因此取值不能太低。推荐在[0.5, 0.8]之间，默认是1.0，即不使用子采样。
  - init: 即我们的初始化的时候的弱学习器，拟合对应原理篇里面的 $f_0(x)$ ，如果不输入，则用训练集样本来做样本集的初始化分类回归预测。否则用init参数提供的学习器做初始化分类回归预测。一般用在我们对数据有先验知识，或者之前做过一些拟合的时候，如果没有的话就不用管这个参数了。
  - loss: 即我们GBDT算法中的损失函数。分类模型和回归模型的损失函数是不一样的。对于分类模型，有对数似然损失函数"deviance"和指数损失函数"exponential"两者输入选择。默认是对数似然损失函数"deviance"。在上原理部分对这些分类损失函数有详细的介绍。一般来说，推荐使用默认的"deviance"。它对二元分离和多元分类各自都有比较好的优化。而指数损失函数等于把我们带到了Adaboost算法。对于回归模型，有均方差"ls", 绝对损失"lad", Huber损失"huber"和分位数损失“quantile”。默认是均方差"ls"。一般来说，如果数据的噪音点不多，用默认的均方差"ls"比较好。如果是噪音点较多，则推荐用抗噪音的损失函数"huber"。而如果我们需要对训练集进行分段预测的时候，则采用“quantile”。
  - alpha：这个参数只有GradientBoostingRegressor有，当我们使用Huber损失"huber"和分位数损失“quantile”时，需要指定分位数的值。默认是0.9，如果噪音点较多，可以适当降低这个分位数的值。
- GBDT类库弱学习器参数，由于GBDT使用了CART回归决策树，因此它的参数基本来源于决策树类，也就是说，和DecisionTreeClassifier和DecisionTreeRegressor的参数基本类似。
  - 划分时考虑的最大特征数max_features: 可以使用很多种类型的值，默认是"None",意味着划分时考虑所有的特征数；如果是"log2"意味着划分时最多考虑 $log_2^N$ 个特征；如果是"sqrt"或者"auto"意味着划分时最多考虑 $\sqrt{N}$ 个特征。如果是整数，代表考虑的特征绝对数。如果是浮点数，代表考虑特征百分比，即考虑（百分比xN）取整后的特征数。其中N为样本总特征数。一般来说，如果样本特征数不多，比如小于50，我们用默认的"None"就可以了，如果特征数非常多，我们可以灵活使用刚才描述的其他取值来控制划分时考虑的最大特征数，以控制决策树的生成时间。
  - 决策树最大深度max_depth: 默认可以不输入，如果不输入的话，默认值是3。一般来说，数据少或者特征少的时候可以不管这个值。如果模型样本量多，特征也多的情况下，推荐限制这个最大深度，具体的取值取决于数据的分布。常用的可以取值10-100之间。
  - 内部节点再划分所需最小样本数min_samples_split: 这个值限制了子树继续划分的条件，如果某节点的样本数少于min_samples_split，则不会继续再尝试选择最优特征来进行划分。默认是2.如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。
  - 叶子节点最少样本数min_samples_leaf: 这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝。默认是1,可以输入最少的样本数的整数，或者最少样本数占样本总数的百分比。如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。
  - 叶子节点最小的样本权重和min_weight_fraction_leaf：这个值限制了叶子节点所有样本权重和的最小值，如果小于这个值，则会和兄弟节点一起被剪枝。默认是0，就是不考虑权重问题。一般来说，如果我们有较多样本有缺失值，或者分类树样本的分布类别偏差很大，就会引入样本权重，这时我们就要注意这个值了。
  - 最大叶子节点数max_leaf_nodes: 通过限制最大叶子节点数，可以防止过拟合，默认是"None”，即不限制最大的叶子节点数。如果加了限制，算法会建立在最大叶子节点数内最优的决策树。如果特征不多，可以不考虑这个值，但是如果特征分成多的话，可以加以限制，具体的值可以通过交叉验证得到。
  - 节点划分最小不纯度min_impurity_split: 这个值限制了决策树的增长，如果某节点的不纯度(基于基尼系数，均方差)小于这个阈值，则该节点不再生成子节点。即为叶子节点。一般不推荐改动默认值1e-7。

使用GBDT解决分类问题

导包，数据集：白酒数据，共有13个特征

import pandas as pd  # 此处用于读取csv文件
import numpy as np   # 用于数据计算处理
from sklearn.model_selection import train_test_split  # 划分数据集
from sklearn.preprocessing import LabelEncoder   # 标签编码
import matplotlib.pyplot as plt  # 绘图
from sklearn.tree import DecisionTreeClassifier  # 从scikitlearn导入决策树模型
from sklearn.ensemble import GradientBoostingClassifier # 从scikitlearn导入GBDT分类模型
from sklearn.metrics import accuracy_score # 从scikitlearn导入评价指标
data_dir = '../RandomForest随机森林/data/'
# Wine dataset and rank the 13 features by their respective importance measures
df_wine = pd.read_csv(data_dir+'wine.data',
                      header=None,
                      names=['Class label', 'Alcohol', 'Malic acid', 'Ash', 'Alcalinity of ash', 'Magnesium',
                               'Total phenols', 'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins', 'Color intensity',
                               'Hue', 'OD280/OD315 of diluted wines', 'Proline'])
print('Class labels', np.unique(df_wine['Class label'])) # 一共有3个类
df_wine = df_wine[df_wine['Class label']!=1] # 去掉一个类
y = df_wine['Class label'].values
X = df_wine[['Alcohol', 'OD280/OD315 of diluted wines']].values
print(len(X),len(y))

```
Class labels [1 2 3]
119 119
```
数据预处理，数据集划分

le = LabelEncoder()   # 实例化
y = le.fit_transform(y)  # 真正进行处理
print('Class labels', np.unique(y))
print('numbers of features:', X.shape[1])
# 划分训练集测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1, stratify=y) # 数据集划分
print(X_train.shape)

Class labels [0 1]
numbers of features: 2
(95, 2)

先使用决策树做分类，作为GBDT的对比参照

tree = DecisionTreeClassifier(criterion='entropy',
                              random_state=1,
                              max_depth=1)
tree = tree.fit(X_train, y_train)      # 决策树训练
y_train_pred = tree.predict(X_train)  # 决策树预测
y_test_pred = tree.predict(X_test)
tree_train = accuracy_score(y_train, y_train_pred)    # 计算准确率
tree_test = accuracy_score(y_test, y_test_pred)
print('Decision tree train/test accuracies %.3f/%.3f' % (tree_train, tree_test))

Decision tree train/test accuracies 0.916/0.875

使用GBDT分类

gbm = GradientBoostingClassifier(n_estimators=500,
                                 learning_rate=0.1,
                                 random_state=1,
                                 criterion='friedman_mse',
                                 max_depth=1,
                                 loss='log_loss')
# 对于分类问题，损失函数默认是"deviance"对数似然损失函数，如果是"exponential"则表示指数损失函数
gbm = gbm.fit(X_train, y_train)
y_train_pred = gbm.predict(X_train)
y_test_pred = gbm.predict(X_test)
gbm_train = accuracy_score(y_train, y_train_pred)
gbm_test = accuracy_score(y_test, y_test_pred)
print('GBDT train/test accuracies %.3f/%.3f' % (gbm_train, gbm_test))

```
GBDT train/test accuracies 1.000/0.917
```
绘制决策边界

def plot_decision_regions(X, y, classifier_list, classifier_names):
    x_min = X[:, 0].min() - 1
    x_max = X[:, 0].max() + 1
    y_min = X[:, 1].min() - 1
    y_max = X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),  # 计算网格
    np.arange(y_min, y_max, 0.1))
    f, axarr = plt.subplots(1, 2, sharex='col', sharey='row', figsize=(8, 3))
    for idx, clf, tt in zip([0, 1],classifier_list,classifier_names):
        clf.fit(X, y)
        Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])  # ravel()方法将数组维度拉成一维数组，np.c_ 用于连接两个矩阵
        Z = Z.reshape(xx.shape)
        axarr[idx].contourf(xx, yy, Z, alpha=0.3)
        axarr[idx].scatter(X[y==0, 0], X[y==0, 1], c='blue', marker='^')
        axarr[idx].scatter(X[y==1, 0], X[y==1, 1], c='red', marker='o')
        axarr[idx].set_title(tt)
        axarr[0].set_ylabel('Alcohol', fontsize=12)
    plt.text(10.2, -0.5, s='OD280/OD315 of diluted wines', ha='center', va='center', fontsize=12)
    plt.show()
plot_decision_regions(X_train, y_train, [tree, gbm], ['Decision Tree', 'GBDT'])

使用AdaBoost+DecisionTree分类树能基本实现GBDT分类问题

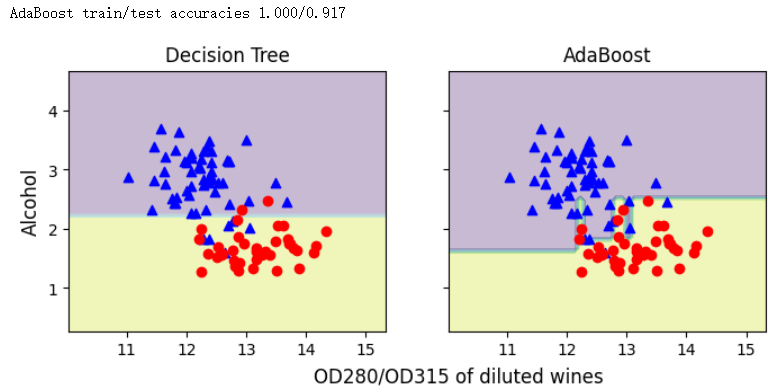
from sklearn.ensemble import AdaBoostClassifier
ada = AdaBoostClassifier(estimator=tree,
                         n_estimators=500,
                         learning_rate=0.1,
                         random_state=1)
ada = ada.fit(X_train, y_train)
y_train_pred = ada.predict(X_train)
y_test_pred = ada.predict(X_test)
ada_train = accuracy_score(y_train, y_train_pred)
ada_test = accuracy_score(y_test, y_test_pred)
print('AdaBoost train/test accuracies %.3f/%.3f' % (ada_train, ada_test))
plot_decision_regions(X_train, y_train, [tree, ada], ['Decision Tree', 'AdaBoost'])