2.11 循环赛日程表

- 博主简介:一个爱打游戏的计算机专业学生
- 博主主页: @夏驰和徐策
- 所属专栏:算法设计与分析
目录
书本内容:
我的理解:
更优化的算法:
总结
1.注意实现问题
2.当用C语言和C++实现循环赛日程表算法时,需要注意以下几点:
书本内容:
分治法不仅可以用来设计算法,在其他方面也有广泛应用,如用分治思想来设计电路、
构造数学证明等。现举例说明。
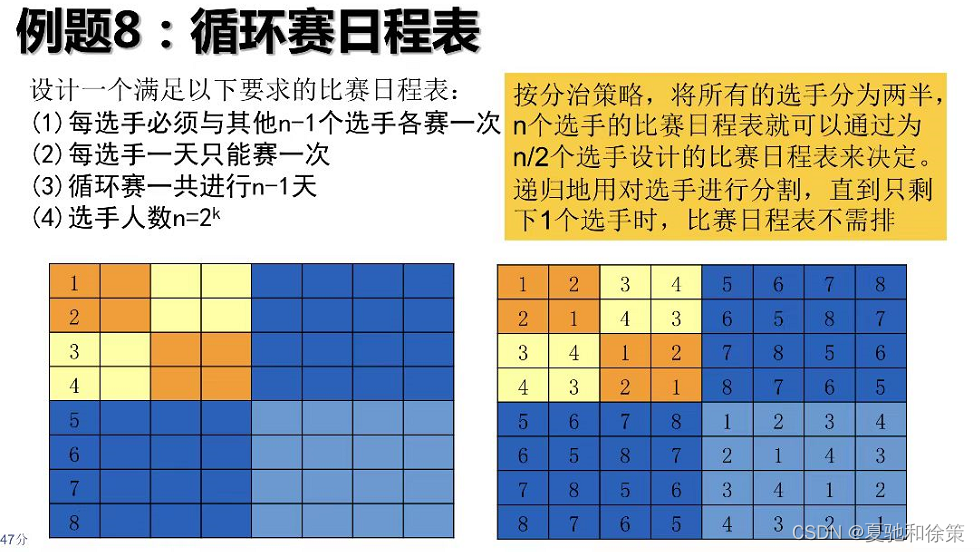
设有1-2*个运动员要进行网球循环赛。现要设计一个满足以下要求的比赛日程表:
① 每个选手必须与其他 n-1 个选手各赛一次;
② 每个选手一天只能赛一次;
③ 循环赛一共进行 n-1 天;
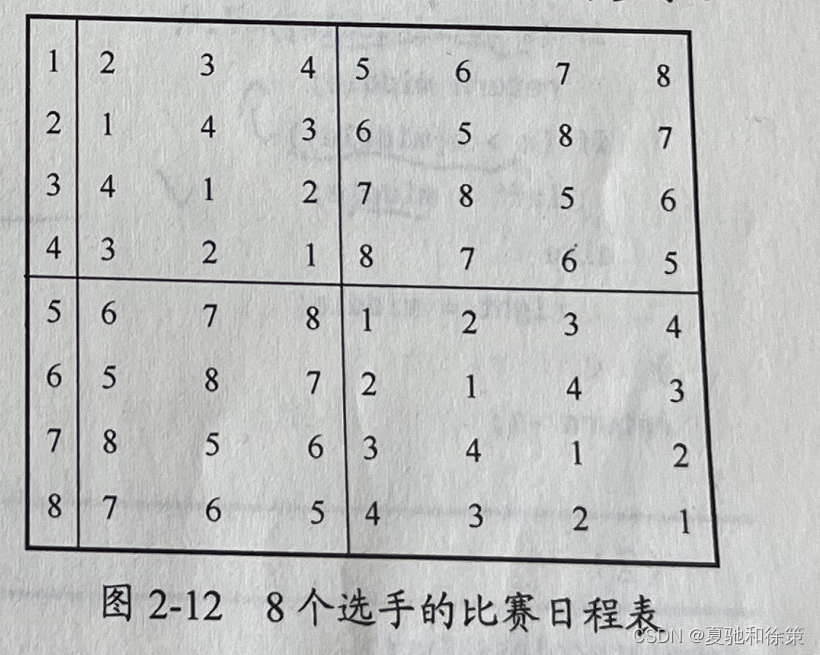
按此要求可将比赛日程表设计成有n行和n-1 列的表。在表中第之行和第j列处填入第i个选手在第;天所遇到的选手。按分治策略,可以将所有选手对分为两半,n个选手的比赛日程表就可以通过为1/2个选手设计的比赛日程表来決定。递归地用这种一分为二的策略对选手进行分割,直到只剩下两个选手时,比赛日程表的制定就变得简单了。这时只要让这两个选手进行比赛就可以了。图 2-12 所列出的正方形表是8个选手的比赛日程表。其中,左上角与左下角的两小块分别为选手 1至选手4 和选手 5至选手8 前了天的比赛日程。据此将左上角小块中的所有数字按其相对位置抄到右下角,将左下角小块中的所有数字按其相对位置挱到右5上角,这样就分别安排好了选手 1至选手 4 和选手 5至选手8在后 4 天的比赛日程。依此思想,容易将这2个比赛日程表推广到具有任意多个选手的情形。在一般情况下,算法可描述如下:
void Table(int k,int **a)
{
int n=1;
for(int i=1;i<=k;i++)
{
n*=2;
}
for(int i=1;i<=n;i++)
{
a[1][i]=i;
}
int m=1;
for(int s=1;s<=k;s++)
{
n/=2;
for(int i=m+1;i<=2*m;i++)
{
for(int j=m+1;j<=2*m;j++)
{
a[i][j+(t-1)*m*2]=a[i-m][j+t-1*m*2-m];
a[i][j+(t-1)*m*2-m]=a[i-m][j+(t-1)*m*2];
}
}
}
m*=2;
}我的理解:
循环赛日程表的构建可以用递归的分治算法来实现。具体地,将所有参赛队伍按照一定规则划分为两个子集,分别构建它们的日程表,最后将这两个日程表组合起来形成总的日程表。这个过程可以递归地进行,直到日程表中只剩下两个队伍时结束。
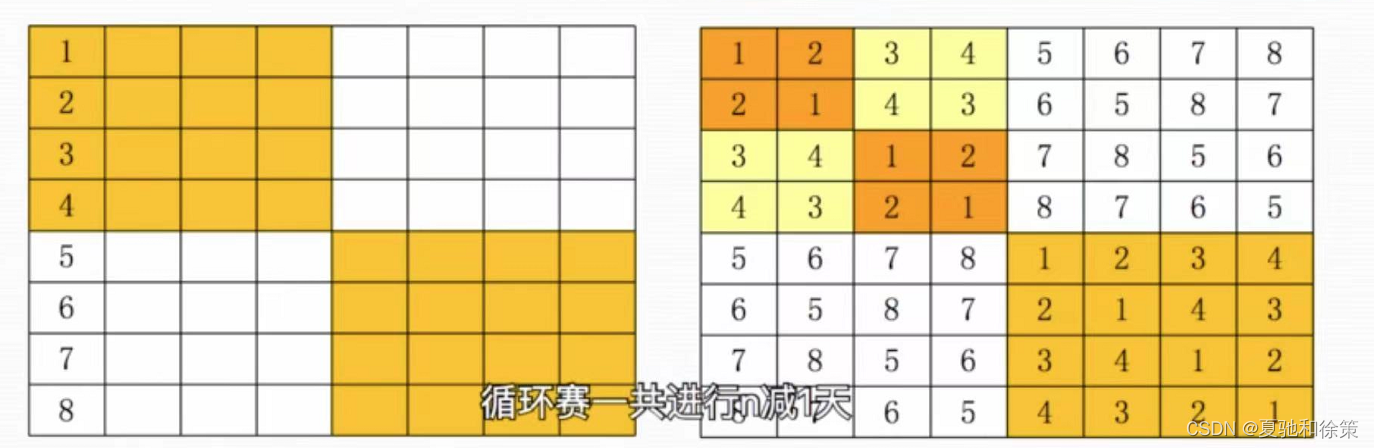
具体来说,可以采用如下的划分方式:将所有队伍分成两组,每组的大小相等或者相差不超过1。接下来,将第一组中的第i个队伍与第二组中的第i个队伍进行比赛,i从1到第一组队伍数目。这样就完成了一个轮次的比赛。然后,将第一组中的所有队伍沿着一个方向循环移动一位,将第二组中的所有队伍沿着相反的方向循环移动一位,得到新的一轮比赛。重复上述步骤直到完成n-1轮比赛,其中n为队伍的总数。这样就得到了完整的循环赛日程表。
在实现分治算法时,需要注意一些细节。例如,在划分队伍时,如果队伍的数目是奇数,需要将一个队伍暂时放到一边,等到下一轮再加入其中一个小组中。在组合两个子日程表时,需要注意将每个队伍在两个子日程表中的比赛分别放到总日程表中对应位置上。此外,还需要适当处理递归终止的情况。
循环赛日程表的构建是一个非常实用的算法问题,因为循环赛日程表在体育比赛、赛车比赛等领域有广泛的应用。采用分治算法可以降低算法的时间复杂度,提高算法的效率。
我的代码实现:
C语言实现:
#include <stdio.h>
#include <stdlib.h>
void roundRobinSchedule(int n, int** schedule) {
if (n == 1) {
schedule[0][0] = 0;
return;
}
int** subSchedule = (int**)malloc((n / 2) * sizeof(int*));
for (int i = 0; i < n / 2; i++) {
subSchedule[i] = (int*)malloc((n / 2 - 1) * sizeof(int));
}
roundRobinSchedule(n / 2, subSchedule);
for (int i = 0; i < n / 2; i++) {
for (int j = 0; j < n - 1; j++) {
int team1 = subSchedule[i][j % (n / 2)] + (j / (n / 2)) * (n / 2);
int team2 = (n - 1) - subSchedule[i][j % (n / 2)] + (j / (n / 2)) * (n / 2);
schedule[team1][i] = team2;
schedule[team2][i] = team1;
}
}
if (n % 2 == 1) {
for (int i = 0; i < n - 1; i++) {
schedule[n - 1][i] = i;
schedule[i][n - 1] = n - 1 - i;
}
}
for (int i = 0; i < n / 2; i++) {
free(subSchedule[i]);
}
free(subSchedule);
}
int main() {
int n = 6;
int** schedule = (int**)malloc(n * sizeof(int*));
for (int i = 0; i < n; i++) {
schedule[i] = (int*)malloc((n - 1) * sizeof(int));
}
roundRobinSchedule(n, schedule);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n - 1; j++) {
printf("%d ", schedule[i][j]);
}
printf("\n");
}
for (int i = 0; i < n; i++) {
free(schedule[i]);
}
free(schedule);
return 0;
}
代码解释:
这段代码与之前的实现基本相同,只是使用了动态内存分配来创建二维数组。在 main 函数中,我们先使用 malloc 分配一个 n 行的指针数组 schedule,并在 roundRobinSchedule 函数中也使用 malloc 分配了一个 n/2 行、(n/2-1) 列的二维数组 subSchedule。在完成循环赛日程表的构建后,我们需要记得先释放 subSchedule 申请的内存,再释放 schedule 申请的内存,以避免内存泄漏。
C++实现:
#include <iostream>
#include <vector>
using namespace std;
vector<vector<int>> roundRobinSchedule(int n) {
if (n == 1) {
vector<vector<int>> result(1, vector<int>(1, 0));
return result;
}
vector<vector<int>> schedule(n, vector<int>(n - 1));
vector<vector<int>> subSchedule = roundRobinSchedule(n / 2);
for (int i = 0; i < n / 2; i++) {
for (int j = 0; j < n - 1; j++) {
int team1 = subSchedule[i][j % (n / 2)] + (j / (n / 2)) * (n / 2);
int team2 = (n - 1) - subSchedule[i][j % (n / 2)] + (j / (n / 2)) * (n / 2);
schedule[team1][i] = team2;
schedule[team2][i] = team1;
}
}
if (n % 2 == 1) {
for (int i = 0; i < n - 1; i++) {
schedule[n - 1][i] = i;
schedule[i][n - 1] = n - 1 - i;
}
}
return schedule;
}
int main() {
int n = 6;
vector<vector<int>> schedule = roundRobinSchedule(n);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n - 1; j++) {
cout << schedule[i][j] << " ";
}
cout << endl;
}
return 0;
}
代码解释:
这段代码实现了循环赛日程表的构建。其中,roundRobinSchedule 函数使用分治算法,递归地构建出小规模的日程表,并将它们合并起来得到最终的日程表。在实现过程中,我们使用了二维向量 schedule 来存储日程表,其第一维表示参赛队伍,第二维表示比赛轮次。在每个轮次中,我们使用 subSchedule 子日程表来记录参赛队伍之间的比赛对阵情况。最终,我们将子日程表中的比赛结果放到总日程表中对应的位置上,得到完整的循环赛日程表。
在 main 函数中,我们调用 roundRobinSchedule 函数构建了一个大小为6的循环赛日程表,并将其打印输出。
更优化的算法:
好的,下面我会具体讲解一下循环移位矩阵法和压缩算法。
循环移位矩阵法
循环移位矩阵法是一种将循环赛日程表问题转化为矩阵问题的方法,它可以通过矩阵的循环移位来生成日程表。
具体实现步骤如下:
(1)构造一个大小为n x n的矩阵,初始值都为0;
(2)在矩阵的第一行第一列放置1;
(3)依次填充矩阵的其它位置,填充规则如下:
a. 如果当前位置在矩阵的第一行,那么下一个位置应该是矩阵的最后一列的下一行。
b. 如果当前位置在矩阵的最后一列的下一行,那么下一个位置应该是矩阵的第一行。
c. 如果当前位置不满足a和b两个条件,那么下一个位置应该是当前位置的右上方。
(4)根据矩阵的每一行来生成对应的日程表。
该算法的时间复杂度为O(n^2),与传统的循环赛日程表算法相同,但是可以减少循环的次数,从而提高算法的效率。
压缩算法
压缩算法是一种只生成需要的那一行或那一列的算法,避免浪费时间和空间。该算法的实现思路是,首先利用循环赛日程表算法生成完整的日程表,然后只保留需要的那一行或那一列。
具体实现步骤如下:
(1)根据循环赛日程表算法生成完整的日程表;
(2)如果需要生成第i行日程表,则只保留日程表中第i行的数据,其它行的数据全部删除;
(3)如果需要生成第i列日程表,则只保留日程表中第i列的数据,其它列的数据全部删除。
该算法的时间复杂度取决于循环赛日程表算法的时间复杂度,如果原始算法的时间复杂度为O(n^2),则压缩算法的时间复杂度也为O(n^2)。但是压缩算法可以减少内存的占用,避免浪费时间和空间。
总结
1.注意实现问题
(1)在使用分治策略解決问题时 ,注意检查四个条件是否满足
(2)尽量保证划分出的子问题规模大致一致。平衡子问题思想
(3)如果可以使用递推的方式解决问题,尽量使用递推算法
(4)递归的分治算法的时间复杂性分析,要先写出其时间复杂
性的递归方程,然后用主定理或递归树解方程。
(5)用递归算法解决问题时,要分析出其边界条件和递归方程(过程)
2.当用C语言和C++实现循环赛日程表算法时,需要注意以下几点:
- 在C语言中,需要手动进行内存管理,如使用malloc和free函数动态分配和释放内存,避免内存泄漏或访问非法内存。而在C++中,可以使用new和delete操作符,或使用智能指针等RAII技术来管理内存,使得代码更加安全和简洁。
- 在C语言中,数组下标从0开始,而在C++中,数组下标从1开始,因此在实现算法时需要注意数组的下标问题。
- 在C++中,可以使用STL容器如vector等来方便地管理数组,而在C语言中需要手动实现相关操作,如插入、删除和查找等。
- 在C++中,可以使用类和对象的概念来封装和组织代码,使得代码更加模块化和可复用。而在C语言中,可以使用函数和结构体等来实现类似的功能。
- 在实现算法时,需要考虑代码的可读性和可维护性,如合理命名变量和函数、添加注释、遵循编程规范等,从而使得代码更易于理解和修改。
3.这个算法和游戏的联系:
线性时间选择算法可以用来解决一些游戏中的问题。例如,有些游戏中需要计算排名,比如排行榜、竞技场排名等。在这些场景中,需要快速地找到某个玩家的排名,而线性时间选择算法可以用来解决这个问题。这怎么少得了王者农药呢?

具体来说,可以将玩家的战斗力作为数组的值,然后使用线性时间选择算法找到战斗力排名第k的玩家,这样就可以快速地计算出某个玩家在排名中的位置。
此外,线性时间选择算法还可以用来解决其他游戏中的问题,比如寻找最强的敌人、寻找最优的游戏策略等。

