考研数二第十二讲 复合函数、反函数、隐函数及参数方程所确定的函数的微分法与一阶微分形式的不变性
复合函数
设函数y=f(u)的定义域为Du,值域为Mu,函数u=g(x)的定义域为Dx,值域为Mx,如果Mx∩Du≠Ø,那么对于Mx∩Du内的任意一个x经过u;有唯一确定的y值与之对应,则变量x与y之间通过变量u形成的一种函数关系,这种函数称为复合函数(composite function),记为:y=f[g(x)],其中x称为自变量,u为中间变量,y为因变量(即函数)。
关于复合函数,我们可以讲复合函数想象成函数嵌套的形式,比如f(g(x))的形式,不在是我们之前认识的简单的f(x)关于x的函数,现在的f函数是一个关于g(x)的函数,而g(x)是关于x的函数,复合函数比较容易和函数求导,函数求间断点,以及函数极限结合起来考察。


复合函数求导(链式法则)


反函数
我们在求一个函数的反函数时,我们只需要将自变量和因变量置换,然后求出类似于y=?x的函数即可。(前提是存在反函数,严格单调函数一定存在反函数,与函数的定义有关)接下来举几
个例子:
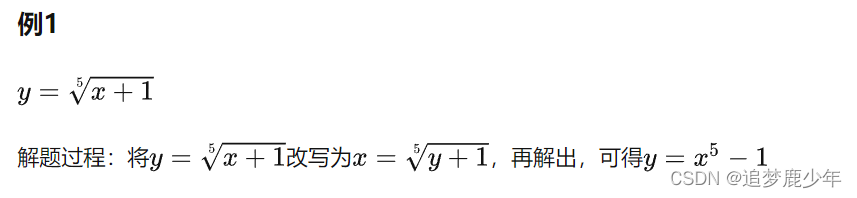
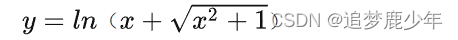

隐函数
如果方程f(x,y)=0能确定y是x的函数,那么称这种方式表示的函数是隐函数。而函数就是指:在某一变化过程中,两个变量x、y,对于某一范围内的x的每一个值,y都有确定的值和它对应,y就是x的函数。这种关系一般用y=f(x)即显函数来表示。f(x,y)=0即隐函数是相对于显函数来说的。
其实隐函数的知识并不难理解,我们以前学的因变量y在函数一边的叫做显函数;隐函数就是将y“隐藏”在一个式子里即和 自变量x在一边的函数。它的难点在于如何利用隐函数求导。接下来,我就和大家聊一聊隐函数的求导。
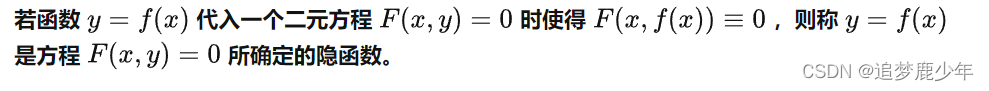




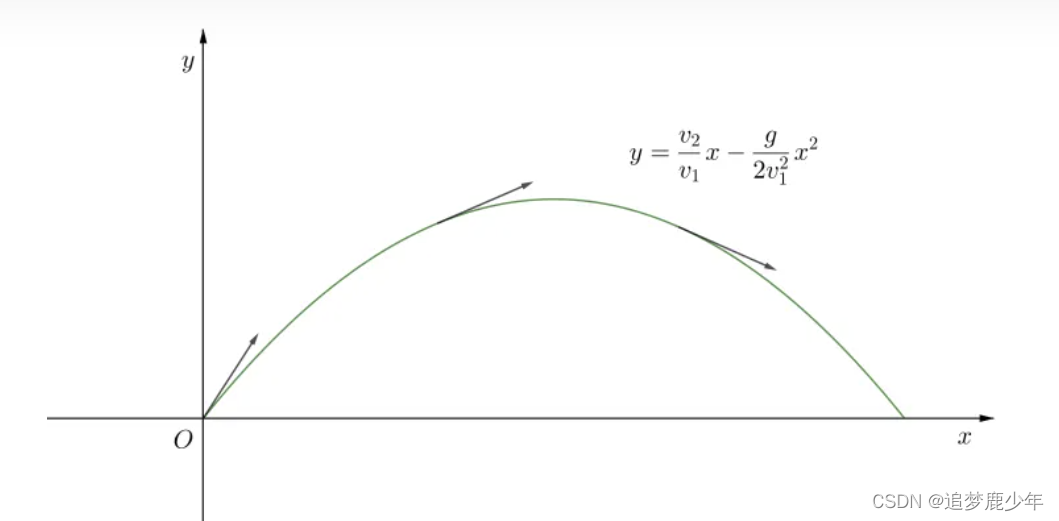
由参数方程所确定的函数的导数






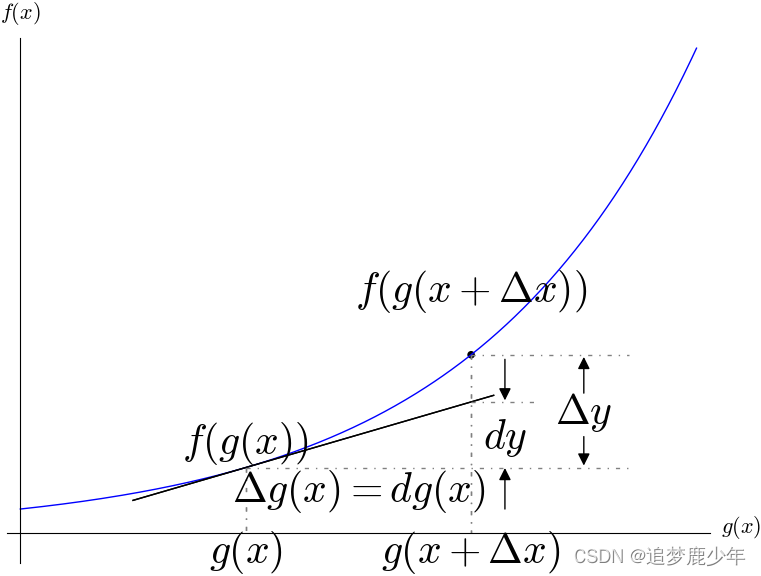
一阶微分形式的不变性
一阶微分不变性,符合高等数学的概念的一贯特点,听上去云山雾罩,一旦明白了,就会觉得,这特么不是理所当然么?
一元函数一阶微分的形式不变性:

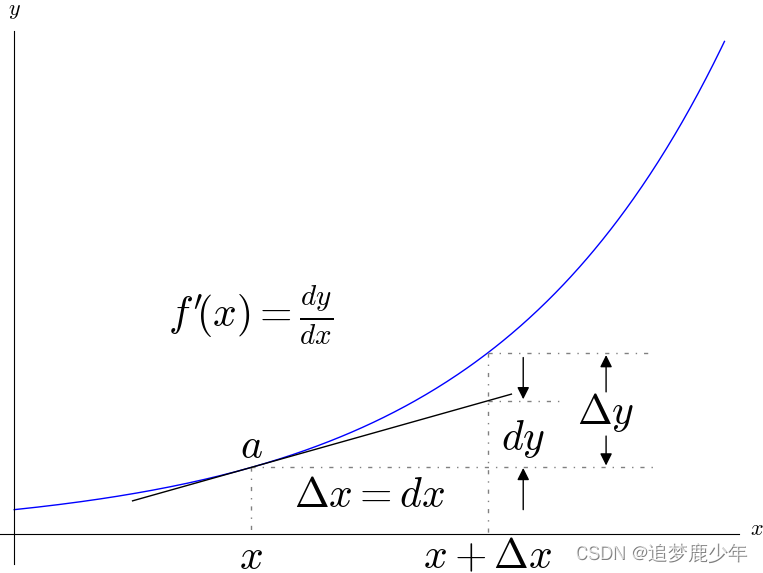
如果是可微函数呢?
函数y=f(g(x)) 函数的导数怎么求,我们来看一下:

费马引理
费马(Fermat)引理:设函数f(x)在点x0的某邻域U(x0)内有定义,并且在x0处可导,如果对任意的x∈U(x0),有f(x)≤f(x0)(或f(x)≥f(xo)),那么f’(x0)=0。
费马引理就是说明,对于某定义区间内的函数极值点,如果该函数在极值点可导,则函数在该极值点的导数为0。体现在几何上,就是在曲线的最高点或最低点处,其切线平行于x轴。
可以通过计算在极值点的左导数和右导数,并且二者必须相等就可以证明。
通常称导数等于0的点为函数的驻点(或稳定点、临界点)。
