1  定义

（1）每个节点是红色或者黑色的。

（2）根节点是黑色的。

（3）所有叶子结点（NIL）都是黑色的。

（4）如果一个节点是红色，则它的两个子节点都是黑色的。

（5）对每个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点。

2  性质

从根到叶节点的最长的可能路径不多于最短的可能路径的两倍。

3  平衡操作

3.1  插入

1、被插入的节点是根节点，直接把此节点设为黑色。

2、被插入的节点的父节点是黑色，当前节点设为红色，然后什么也不需要做。

3、被插入的节点的父节点是红色

（1）当前节点的叔节点也是红色

        ① 将父节点设为黑色

        ② 将叔节点设为黑色

        ③ 将祖父节点设为红色

        ④ 将祖父节点设为当前节点（红色节点）；之后继续对当前节点进行操作。

（2）当前节点的叔节点是黑色，且当前节点是其父节点的右孩子

        ① 将父节点作为新的当前节点

        ② 以新的当前节点为支点进行左旋

（3）当前节点的叔节点是黑色，且当前节点是其父节点的左孩子

        ① 将父节点设为黑色

        ② 将祖父节点设为红色

        ③ 以祖父节点为支点进行右旋

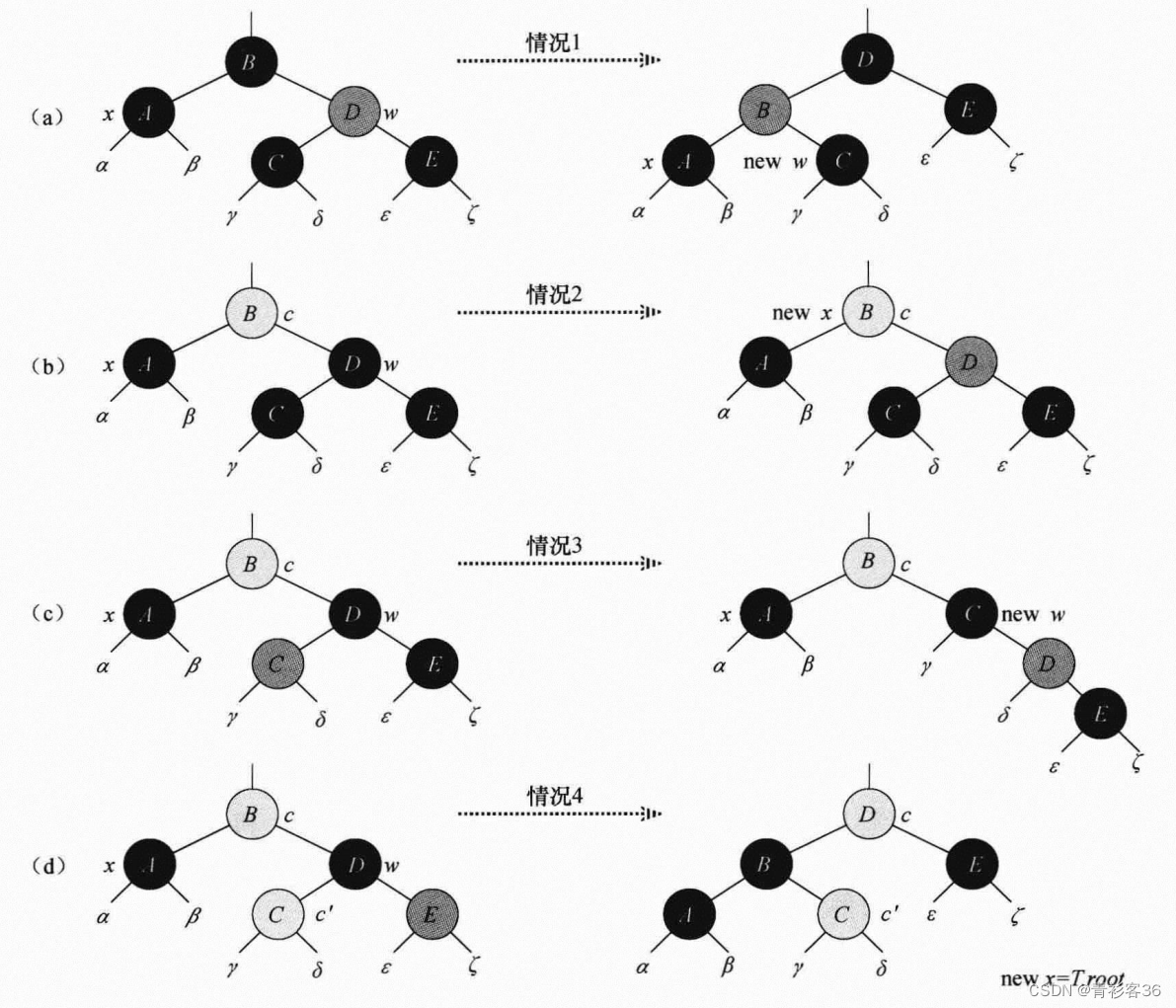
3.2  删除

红黑树的删除操作是在二叉搜索树的删除操作后，再去维护红黑树的性质。首先，如果我们删除的是红色点，那么对红黑树的性质没有影响，不需要为了维护红黑树的性质而做额外的操作；如果删除的是一个黑色点，那么我们一定会提上来一个点（类比二叉排序树的节点删除操作），那么我们就把黑色点累加到提上来的点上，也就是说这个点上包含两个颜色（红+黑 或者 黑+黑），这样的话，我们虽然删掉了一个黑色点，但是它的颜色被留下来了，此时仍然可以满足任意一条路径上所有的黑色点的数目都是一样的。

1、x指向一个“红 + 黑”节点，将x设为一个黑节点即可

2、x指向根，将x设为一个黑节点即可

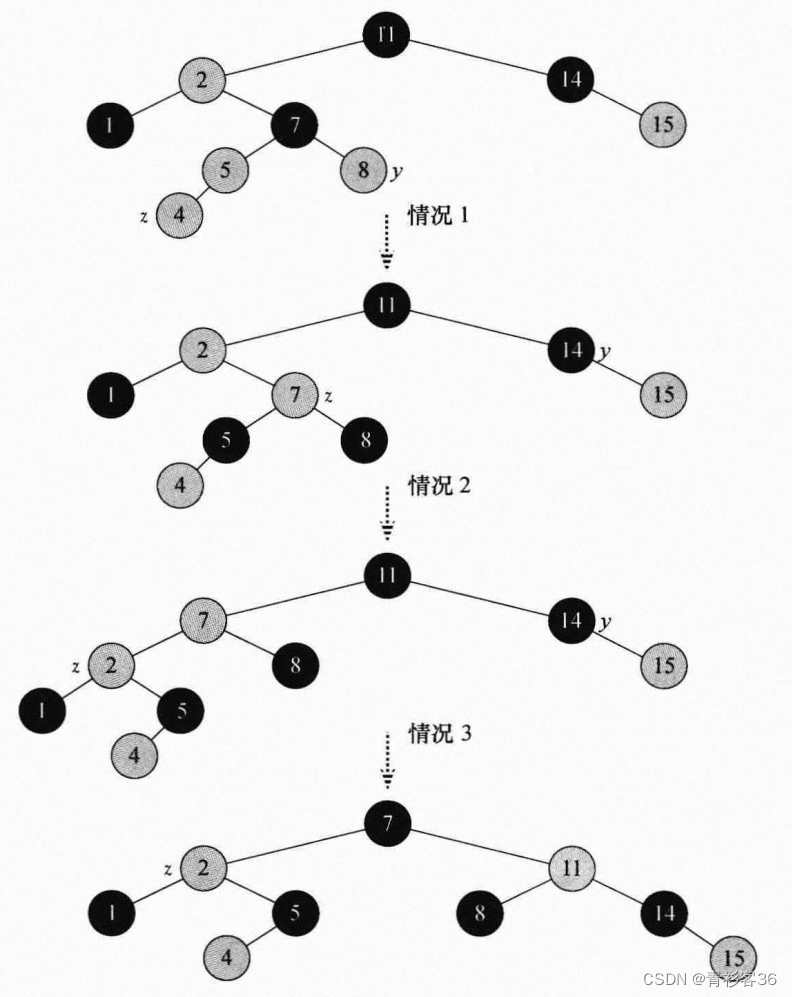
3.1、x的兄弟节点是红色

        （1）将x的兄弟节点设为黑色

        （2）将x的父节点设为红色

        （3）对x的父节点进行左旋

        （4）左旋后，重新设置x的兄弟节点。

（注：3.1步做完之后当前节点x的兄弟节点一定是黑色，即3.1步执行结束后转换为3.2、3.3、3.4）

3.2、x的兄弟节点是黑色，x的兄弟节点的两个孩子都是黑色

        （1）将x的兄弟节点设为红色

        （2）设置x的父节点为新的x节点（将当前节点“黑+黑”的其中一个黑，赋给父节点）

注：3.2步完成之后的效果是将处理的节点往上移动一层

3.3、x的兄弟节点是黑色，x的兄弟节点的左孩子是红色，右孩子是黑色

        （1）将x兄弟节点的左孩子设为黑色

        （2）将x兄弟节点设为红色

        （3）对x的兄弟节点进行右旋

        （4）右旋后，重新设置x的兄弟节点

注：3.3步的作用是将情况3.3转换成情况3.4

3.4、x的兄弟节点是黑色，x的兄弟节点的右孩子是红色的，x的兄弟节点的左孩子任意颜色

        （1）将x父节点颜色赋值给x的兄弟节点

        （2）将x父节点设置为黑色

        （3）将x兄弟节点的右子节点设为黑色

        （4）对x的父节点进行左旋

注：执行完3.4就可解决红黑树的删除操作导致的性质不满足问题