数据结构之（三）：队列

队列，是一种对存取有严格要求的数据结构

只能从尾部存入数据，从头部取出数据

遵循 “ 先进先出 ” 原则

队列的实现有两种方式：

顺序队列（基于数组）、链队列（基于链表）

 用数组实现队列

public class ArrayQueue {
    // 最大容量
    int maxCapacity;
    // 声明头尾指针
    int head;
    int tail;
    // 存储元素
    int[] arr;
    public ArrayQueue(int maxCapacity) {
        arr = new int[maxCapacity];
        maxCapacity = maxCapacity;
        head = 0;
        tail = 0;
    }
    public boolean isFull() {
        return tail == maxCapacity;
    }
    public void add(int n) {
// 先判断队列的容量大小
        if (!isFull()) {
            arr[tail] = n;
        }
    }
    public boolean isEmpty() {
        return head == tail;
    }
    public int get() {
// 先判断队列是否为空
        if (isEmpty()) return -1;
        int result = arr[head];
        head++;
        return result;
    }
}

    public static void main(String[] args) {
        Queue<Integer> queue = new LinkedList<>();
// 都能添加元素
// queue.add(1);
        queue.offer(1);
        queue.offer(2);
        queue.offer(3);
// 两者区别 当队列满的时候 add会抛出异常 offer会返回false 更健壮更友好
// 取出元素 分为两种
// 只获取队头元素 不取出
        queue.peek();
        queue.element();
// 两者区别 当队列为空时 element会抛出异常 peek会返回null
// 获取队头元素 同时取出
        queue.poll();
        queue.remove();
// 两者区别 当队列为空时 remove会抛出异常 poll会返回null
    }

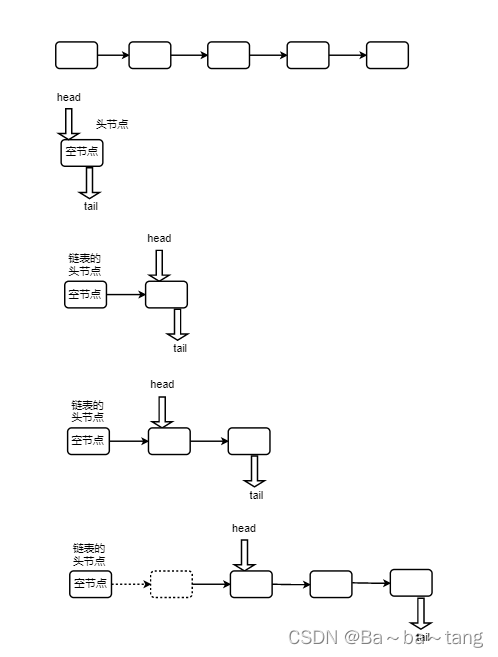
 双端队列和各式队列

双端队列

双端队列，区别于普通队列

两端都可以进行入队和出队

deque = "double ended queue"

LinkedList 和 ArrayDeque

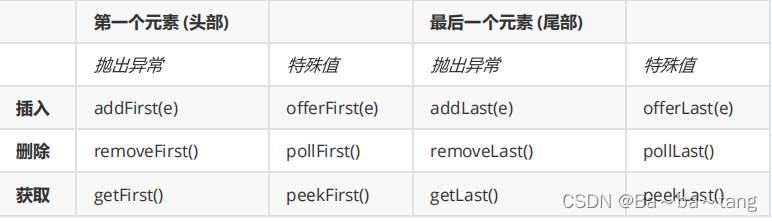
 【特别的队列】

1 ） 优先级队列

元素携带了相关的优先级，优先级更高的元素排在头部

PriorityQueue ，提供了 Comparable 接口，元素可以实现其方法，改变在队列中的顺序

2 ）阻塞队列

当队列满的时候，等待有空余位置再存数据；当队列空的时候，等待有新数据再读取

BlockingQueue ， put() 和 take() 提供了存取的阻塞逻辑

分为两种情况，一种是无限期的等，一种是指定阻塞时间

3 ）延迟队列

在指定时间内获取队列元素，头部元素是最接近过期时间的。

DelayQueue 给定一个接口设置延迟时间 元素会按照时间排序

https://leetcode-cn.com/problems/dui-lie-de-zui-da-zhi-lcof/

剑指 Offffer 59 - II. 队列的最大值

请定义一个队列并实现函数 max_value

得到队列里的最大值，要求函数 max_value 、 push_back 和 pop_front 的均摊时间复杂度都是

O(1) 。

若队列为空， pop_front 和 max_value 需要返回 -1

示例 1 ：

输入 :

["MaxQueue","push_back","push_back","max_value","pop_front","max_value"]

[[],[1],[2],[],[],[]]

输出 : [null,null,null,2,1,2]

分别对应 方法名、参数 以及 返回结果

示例 2 ：

输入 :

["MaxQueue","pop_front","max_value"]

[[],[],[]]

输出 : [null,-1,-1]

分析：

队头 队尾

[1,2,3,4,3,2,1]

在队列发生更改时 记录出最大值

[] -1

[1] 1

[1,2] 2

[1,2,3] 3

[2,3] 3

[2,3,2,1] 3

[3,2,1] 3

[2,1] 2

因为增删操作时 都可能影响最大值的变化

如果是新增操作，比较新元素和当前最大值之间，更大的值是新的最大值

如果是删除操作，删除的元素如果不是最大值，那么最大值不变，如果是最大值，最大值要更改为剩余

元素的最大值

使用额外的队列，来记录最大值发生的变化

max 队列，队头元素是当前的最大值，而其他元素是未来可能成为最大值的候选值

新增元素 ele 时 ele>max 取队列中队尾元素比较，如果满足，进行覆盖并且循环比较

直到把所有比它小的值都覆盖为止

ele<max 将其存到 max 队列中

原队列 max 队列

[1] [1]

[1,2] [2]

[1,2,3] [3]

[2,3] [3]

[2,3,2] [3,2]

[2,3,2,1] [3,2,1]

[3,2,1] [3,2,1]

[2,1] [2,1]

[2,1,4] [4]

public class MaxQueue {
    // 原始队列
    LinkedList<Integer> queue;
    // 最大值的候选值
    LinkedList<Integer> max;
    public MaxQueue() {
        queue = new LinkedList<>();
        max = new LinkedList<>();
    }
    public int max_value() {
        if (max.isEmpty()) return -1;
        return max.peekFirst();
    }
    // 新增元素 ele时 ele>max 取队列中队尾元素比较，如果满足，进行覆盖并且循环比较
// 直到把所有比它小的值都覆盖为止
// ele<max 将其存到max队列中
    public void push_back(int value) {
        queue.offer(value);
        while (!max.isEmpty() && max.peekLast() < value) {
            max.pollLast();
        }
        max.add(value);
    }
    public int pop_front() {
// 如果删除的元素是最大值 从max队列中同时删掉
        if (!max.isEmpty() && queue.peekFirst().equals(max.peekFirst())) {
            max.pollFirst();
        }
        if (queue.isEmpty()) return -1;
        return queue.poll();
    }
}

剑指 Offffer 59 - I. 滑动窗口的最大值

给定一个数组 nums 和滑动窗口的大小 k ，请找出所有滑动窗口里的最大值。

示例 :

输入 : nums = [1,3,-1,-3,5,3,6,7], 和 k = 3

输出 : [3,3,5,5,6,7]

解释 :

滑动窗口的位置 最大值

[1 3 -1] -3 5 3 6 7 3

1 [3 -1 -3] 5 3 6 7 3

1 3 [-1 -3 5] 3 6 7 5

1 3 -1 [-3 5 3] 6 7 5

1 3 -1 -3 [5 3 6] 7 6

1 3 -1 -3 5 [3 6 7] 7

分析：

数组的长度为 n 窗口的大小为 k 可形成的窗口个数 n-k+1

通过队列来记录最大值

窗口未形成的阶段

遍历数组，同时更新队列

窗口已形成的阶段

每次窗口移动，都是在头部移除元素，尾部增加元素

在窗口变化过程中 记录其最大值的变化 ( 让最大值一直出现在第一位 )

让队列中已存在的元素 和新添加的元素比较 如果已存在的更小 那么覆盖

如果已存在的更大 新添加的元素是候选 缀到队列之后

滑动窗口的位置 最大值

public static int[] maxSlidingWindow(int[] nums, int k) {
// 记录每个窗口的最大值 n-k+1为形成的窗口个数
        int[] result = new int[nums.length - k + 1];
// 使用队列记录最大值的候选值
        Deque<Integer> deque = new ArrayDeque<>();
// 窗口未形成的阶段
        for (int i = 0; i < k; i++) {
            print(deque);
// 每次都取 队尾元素和新元素 比较 如果队尾更小 删除
            while (!deque.isEmpty() && deque.peekLast() < nums[i]){
                deque.pollLast();
            }
            deque.offerLast(nums[i]);
        }
// 此时第一个窗口形成 deque的队头元素就是第一个窗口的最大值
        result[0] = deque.peekFirst();
        print(deque);
// 窗口已形成的阶段
        for (int i = k; i < nums.length; i++) {
            System.out.println("-----第" + (i-k+1) + "次滑动");
// 删了元素 nums[i-k] 添了元素 nums[i]
            if(nums[i-k] == deque.peekFirst()){
// 如果删的是最大值 同时从deque移除
                deque.pollFirst();
            }
// 新增
            while (!deque.isEmpty() && deque.peekLast() < nums[i]){
                deque.pollLast();
            }
            deque.offerLast(nums[i]);
            result[i-k+1] = deque.peekFirst();
            print(deque);
        }
        return result;
    }
    public static void print(Deque<Integer> deque){
        for (Integer integer : deque) {
            System.out.print(integer + " ");
        }
        System.out.println();
    }
}

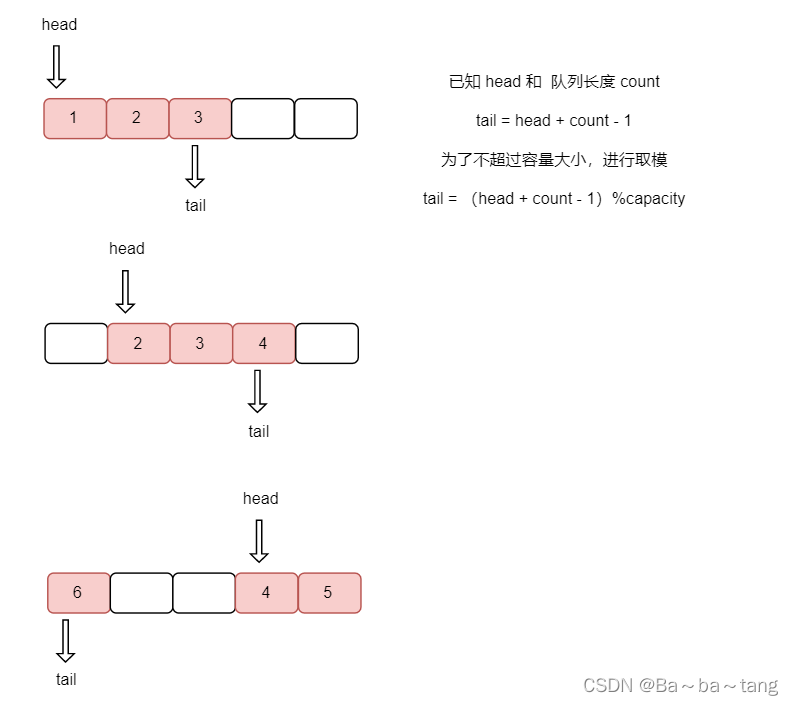
循环队列

为解决，队列存取数据后，空间无法重复利用的问题，通过构造环形，重复使用

622. 设计循环队列

设计你的循环队列实现。 循环队列是一种线性数据结构，其操作表现基于 FIFO （先进先

出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为 “ 环形缓冲器 ” 。

循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队

列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使

用这些空间去存储新的值。

你的实现应该支持如下操作：

MyCircularQueue(k): 构造器，设置队列长度为 k 。

Front: 从队首获取元素。如果队列为空，返回 -1 。

Rear: 获取队尾元素。如果队列为空，返回 -1 。

enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。

deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。

isEmpty(): 检查循环队列是否为空。

isFull(): 检查循环队列是否已满。

public class MyCircularQueue {
    // 存储元素的数组
    int[] queue;
    // 最大容量
    int capacity;
    // 头指针
    int head;
    // 实际队列长度
    int count;
    /**
     * Initialize your data structure here. Set the size of the queue to be k.
     */
    public MyCircularQueue(int k) {
        capacity = k;
        queue = new int[k];
        head = 0;
        count = 0;
    }
    /**
     * Insert an element into the circular queue. Return true if the operation
     is successful.
     */
    public boolean enQueue(int value) {
        if (isFull()) return false;
        int index = (head + count) % capacity;
        queue[index] = value;
        count++;
        return true;
    }
    /**
     * Delete an element from the circular queue. Return true if the operation
     is successful.
     */
    public boolean deQueue() {
        if (isEmpty()) return false;
        head = (head + 1) % capacity;
        count--;
        return true;
    }
    /**
     * Get the front item from the queue.
     */
    public int Front() {
        if (isEmpty()) return -1;
        return queue[head];
    }
    /**
     * Get the last item from the queue.
     */
    public int Rear() {
        if (isEmpty()) return -1;
        int tail = (head + count - 1) % capacity;
        return queue[tail];
    }
    /**
     * Checks whether the circular queue is empty or not.
     */
    public boolean isEmpty() {
        return count == 0;
    }
    /**
     * Checks whether the circular queue is full or not.
     */
    public boolean isFull() {
        return count == capacity;
    }
}